PDE 与机器学习（四）—— 变分推断与 Fokker-Planck 方程

概率推断是机器学习的核心问题之一。给定观测数据，我们希望推断出隐变量的后验分布，或者从复杂的高维分布中采样。传统方法分为两大类：变分推断（ Variational Inference, VI）通过优化变分下界来近似后验分布，而马尔可夫链蒙特卡洛（ MCMC）通过构造马尔可夫链来采样。这两种看似不同的方法，在偏微分方程的视角下却展现出深刻的统一性。

当我们用 Langevin 动力学进行 MCMC 采样时，粒子在势能场中的运动由随机微分方程描述，其概率密度演化遵循 Fokker-Planck 方程；当我们用梯度下降优化变分下界时，参数分布在 Wasserstein 空间中的演化同样可以视为某个能量泛函的梯度流。更令人惊奇的是，KL 散度的最小化过程本身就是 Fokker-Planck 方程的解——变分推断与 Langevin MCMC 在连续时间极限下完全等价。这种 PDE 视角不仅揭示了概率推断的数学本质，还为设计新的推断算法（如 Stein 变分梯度下降）提供了统一的理论框架。

本文将系统性地建立这一理论框架。我们从 Fokker-Planck 方程出发，展示如何将随机过程的概率密度演化形式化为偏微分方程；然后深入 Langevin 动力学，讨论过阻尼与欠阻尼情况，以及 It ô与 Stratonovich 积分的区别；接着建立 KL 散度的梯度流解释，证明变分推断与 Langevin MCMC 的等价性；最后聚焦 Stein 变分梯度下降等前沿方法，展示如何用粒子系统求解变分推断问题，并通过四个完整实验验证理论预测。

引言：概率推断的 PDE 视角

概率推断的基本问题

贝叶斯推断：给定观测数据和先验分布，我们希望计算后验分布 $$

p(z|x) = = $$

对于复杂模型，后验分布通常无法解析计算（分母的积分难以求解），因此需要近似方法。

变分推断：用一个简单的分布族来近似后验分布，通过最小化 KL 散度：

等价地最大化证据下界（ ELBO）：

MCMC 方法：构造马尔可夫链，使得其平稳分布为后验分布。常用的方法包括 Metropolis-Hastings 、 Gibbs 采样、以及Langevin 动力学。

PDE 视角的统一框架

从 PDE 视角看，这两种方法都涉及概率测度空间上的演化：

Langevin MCMC：粒子遵循随机微分方程 $$

dz_t = -U(z_t) dt + dW_t $$

其中是势能函数，是温度参数。概率密度的演化由Fokker-Planck 方程控制：

变分推断：参数分布在 Wasserstein 空间中演化，最小化 KL 散度。可以证明，这一演化过程同样由 Fokker-Planck 方程描述，只是初始条件和边界条件不同。
Stein 变分梯度下降：用粒子系统近似分布，每个粒子遵循

其中是核函数。这可以视为 Fokker-Planck 方程在有限粒子近似下的离散化。

本文结构

本文按以下结构展开：

Fokker-Planck 方程与概率密度演化：从随机微分方程推导 Fokker-Planck 方程，讨论其物理意义和数学性质。
Langevin 动力学：详细讨论过阻尼与欠阻尼 Langevin 方程， It ô与 Stratonovich 积分的区别，以及数值求解方法。
KL 散度的梯度流解释：证明 KL 散度最小化等价于 Fokker-Planck 方程的求解，建立变分推断与 Langevin MCMC 的联系。
变分推断与 Langevin MCMC 的等价性：在连续时间极限下，证明两种方法的等价性。
Stein 变分梯度下降：介绍 SVGD 方法，展示如何用粒子系统求解变分推断问题。
实验验证：通过四个实验验证理论预测。

Fokker-Planck 方程与概率密度演化

从随机微分方程到 Fokker-Planck 方程

考虑一般的随机微分方程（ SDE）： $$

dX_t = (X_t, t) dt + (X_t, t) dW_t $$

其中是漂移项（ drift），是扩散项（ diffusion），是维标准布朗运动。

Fokker-Planck 方程（也称为 Kolmogorov 前向方程）描述了概率密度函数的演化：

其中是扩散矩阵。

向量形式：

其中表示散度算子。

推导：从 SDE 到 Fokker-Planck 方程

思路：考虑任意光滑函数，计算的时间导数。

由 It ô引理： $$

df(X_t) = {i=1}^d dX{i,t} + {i,j=1}^d dX{i,t} dX_{j,t} $$

代入 SDE： $$

df(X_t) = {i=1}^d [i dt + {k=1}^m {ik} dW{k,t}] + {i,j=1}^d D_{ij} dt $$

取期望：

另一方面：

因此：

对右边进行分部积分（假设边界项为零）：

因此：

由于任意，得到 Fokker-Planck 方程。

特殊形式： Langevin 动力学对应的 Fokker-Planck 方程

对于过阻尼 Langevin 动力学： $$

dX_t = -U(X_t) dt + dW_t $$

其中是势能函数，是温度参数。

对应的 Fokker-Planck 方程为：

平衡分布：当时，如果存在平衡分布，则，因此：

可以验证，Gibbs 分布 是平衡分布：

验证：

因此：

Fokker-Planck 方程的性质

概率守恒：如果初始分布满足，则对任意有。

证明：（由散度定理，边界项为零）

熵增原理：对于扩散过程，熵（负对数似然）随时间增加： $$

H(t) = -(x,t) (x,t) dx = - (1 + ) dx $$

代入 Fokker-Planck 方程，可以证明（当扩散矩阵正定时）。

H 定理：对于 Langevin 动力学，如果平衡分布是 Gibbs 分布，则相对熵（ KL 散度）单调递减：

这保证了分布收敛到平衡分布。

Langevin 动力学：过阻尼与欠阻尼

过阻尼 Langevin 方程

物理背景：在粘性介质中，粒子的惯性可以忽略，运动完全由摩擦力和随机力驱动。

过阻尼 Langevin 方程： $$

dX_t = -^{-1} U(X_t) dt + dW_t $$

其中是摩擦系数。通常设，得到标准形式： $$

dX_t = -U(X_t) dt + dW_t $$

对应的 Fokker-Planck 方程：

数值求解：Euler-Maruyama 方法（一阶）： $$

X_{n+1} = X_n - U(X_n) + _n $$

其中是步长，。

改进方法：Metropolis-adjusted Langevin algorithm (MALA) 在每步后添加 Metropolis 接受-拒绝步骤，保证精确采样。

欠阻尼 Langevin 方程

物理背景：考虑粒子的惯性，运动由位置和速度共同描述。

欠阻尼 Langevin 方程（二阶 SDE）：

其中是速度，是摩擦系数。

相空间 Fokker-Planck 方程：概率密度在相空间中演化：

其中和分别表示对位置和速度的梯度。

平衡分布： Gibbs 分布

数值求解：Hamiltonian Monte Carlo (HMC) 可以视为欠阻尼 Langevin 动力学的离散化。

It ô vs Stratonovich 积分

在随机微分方程中，积分有两种定义方式：

It ô积分：

Stratonovich 积分：

区别： - It ô积分：被积函数在区间左端点取值，不满足链式法则 - Stratonovich 积分：被积函数在区间中点取值，满足链式法则（类似经典微积分）

转换关系：对于 SDE $$

dX_t = (X_t) dt + (X_t) dW_t $$

等价于 It ô形式： $$

dX_t = dt + (X_t) dW_t $$

在 Langevin 动力学中的应用：通常使用 It ô积分，因为： 1. 数学上更简单（鞅性质） 2. 数值方法更直接（ Euler-Maruyama） 3. Fokker-Planck 方程形式更简洁

KL 散度的梯度流解释

Wasserstein 梯度流

Wasserstein 距离：对于两个概率测度，$ p $距离定义为：$ $

W_p(, ) = (_{(,)} |x-y|^p d(x,y))^{1/p} $$

其中是所有以为边缘分布的耦合测度。

Wasserstein 梯度流：考虑能量泛函，其 Wasserstein 梯度流为：

其中是泛函导数。

KL 散度作为能量泛函

考虑 KL 散度：

其中是目标分布。

泛函导数：

Wasserstein 梯度流：

展开：

由于，有，因此：

这恰好是 Fokker-Planck 方程（当时）！

梯度流与 Langevin 动力学的等价性

定理： KL 散度的 Wasserstein 梯度流等价于 Langevin 动力学的 Fokker-Planck 方程。

证明：我们已经看到， KL 散度的梯度流给出：

而 Langevin 动力学的 Fokker-Planck 方程为：

两者相同。 物理意义： - 变分推断：在 Wasserstein 空间中，沿着 KL 散度的负梯度方向演化，使分布逐渐接近目标分布 - Langevin MCMC：粒子在势能场中运动，概率密度演化同样使分布接近目标分布 - 统一性：两种方法在连续时间极限下完全等价

收敛性分析

定理（收敛性）：如果目标分布满足对数 Sobolev 不等式（ log-Sobolev inequality），则 KL 散度以指数速率收敛：

其中是对数 Sobolev 常数。

对数 Sobolev 不等式：存在常数，使得对任意函数 $ f $：$ $

其中是熵。

变分推断与 Langevin MCMC 的联系

离散时间视角

变分推断：优化参数，使 $Missing superscript or subscript argument q_$ 接近 $ p(z|x) $：$ $

Langevin MCMC：采样粒子，使经验分布接近 $ p(z|x) $：$ $

z_{t+1} = z_t - _z p(z_t|x) + _t $$

连续时间极限

变分推断的连续时间极限：当参数分布演化时，如果使用自然梯度（ natural gradient），则：

这恰好是 KL 散度的 Wasserstein 梯度流。

Langevin MCMC 的连续时间极限：当粒子数时，经验分布的演化由 Fokker-Planck 方程描述。

等价性：两种方法在连续时间极限下给出相同的 PDE，因此等价。

实际应用中的区别

虽然理论上等价，但在实际应用中：

变分推断：
- 优点：计算效率高（一次前向传播），可并行
- 缺点：需要选择变分族，可能有近似误差
Langevin MCMC：
- 优点：渐近精确（当），不需要选择变分族
- 缺点：需要长时间运行，难以并行
混合方法：结合两者优点，如变分 Langevin 动力学（ Variational Langevin Dynamics）。

Stein 变分梯度下降（ SVGD）

动机：粒子变分推断

传统变分推断需要选择参数化分布族（如高斯分布），这限制了表达能力。Stein 变分梯度下降（ Stein Variational Gradient Descent, SVGD）用粒子系统 $Extra close brace or missing open brace\{z_i} _{i=1}^n$ 来近似分布，无需显式参数化。

Stein 方法基础

Stein 算子：对于函数 $ k: ^d ^d $（核函数），定义算子：$ $

其中是目标分布。

Stein 恒等式：如果，则对任意函数 $ f $：$ $

Stein 差异（ Stein discrepancy）：

其中是函数类（通常取为再生核 Hilbert 空间 RKHS）。

SVGD 算法

目标：最小化 Stein 差异，其中是粒子系统的经验分布。

关键洞察：在 RKHS 中，最优方向函数为：

SVGD 更新规则： $$

z_i z_i + ^{*}(z_i) = z_i + _{j=1}^n [k(z_j, z_i) {z_j} p(z_j) + {z_j} k(z_j, z_i)] $$

其中是步长。

SVGD 的 PDE 解释

连续时间极限：当粒子数时，经验分布的演化由以下 PDE 描述：

其中。

展开：

这可以视为非局部的 Fokker-Planck 方程，其中核函数引入了粒子间的相互作用。

SVGD vs Langevin MCMC

相似性： - 都使用粒子系统 - 都通过演化使分布接近目标分布

区别： - Langevin MCMC：每个粒子独立演化，通过随机噪声探索 - SVGD：粒子通过核函数相互作用，形成排斥力，避免粒子聚集

优势： - SVGD 通常收敛更快（粒子间相互作用） - SVGD 不需要随机噪声，确定性更新 - SVGD 可以处理多峰分布（粒子自动分散到不同模式）

实验验证

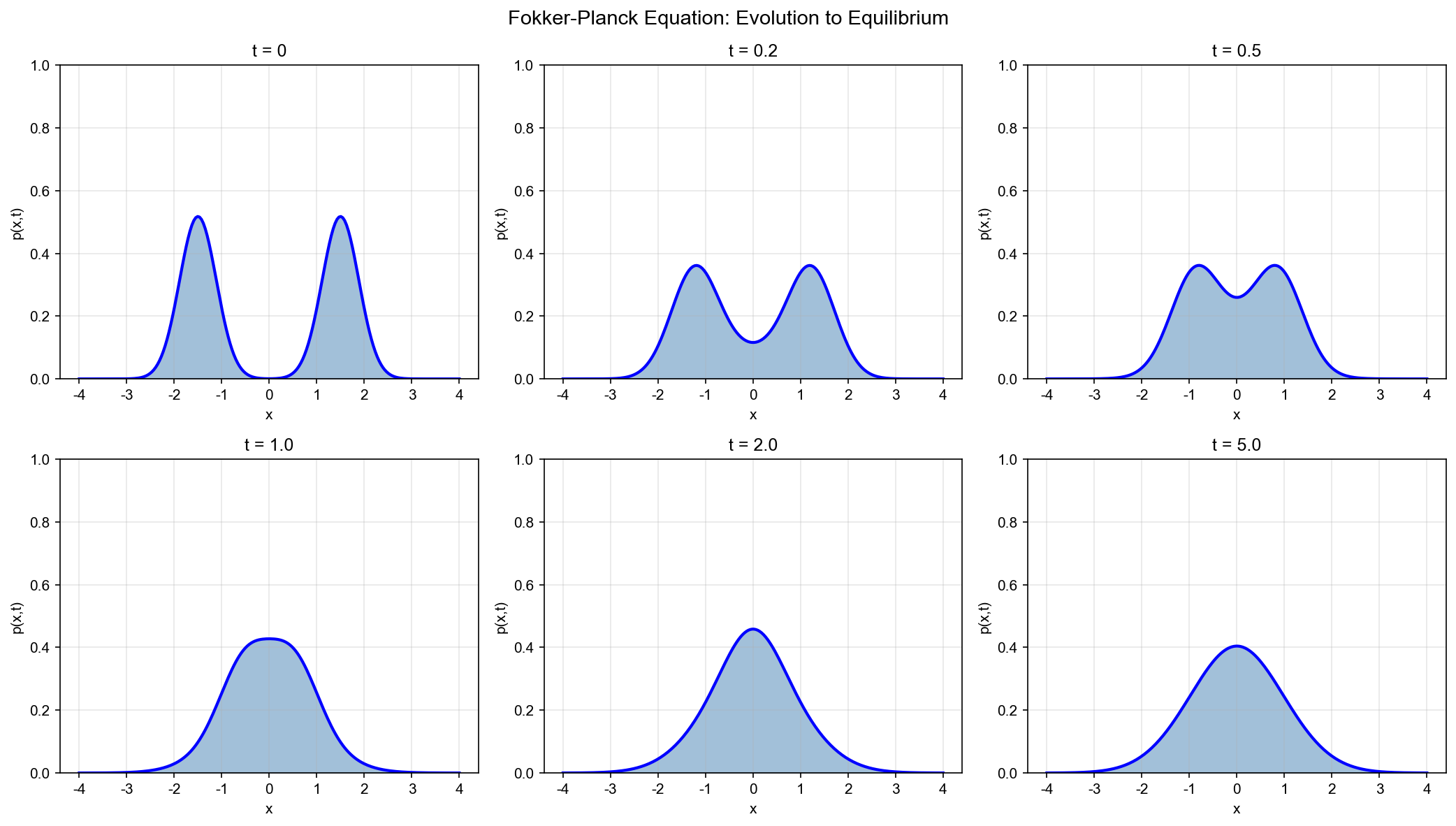
实验 1：一维 Fokker-Planck 演化可视化

目标：可视化 Fokker-Planck 方程的解，展示概率密度如何演化到平衡分布。

设置： - 势能函数：（双峰） - 初始分布： - 平衡分布：方法：数值求解 Fokker-Planck 方程（有限差分法）。完整代码见 experiment1_fokker_planck.py。

关键步骤： 1. 离散化空间：将离散化为 200 个点 2. 时间积分：使用 scipy.integrate.odeint 求解 ODE 系统 3. 边界条件：使用零边界条件（反射边界） 4. 可视化：展示不同时刻的概率密度演化，以及 KL 散度随时间的变化

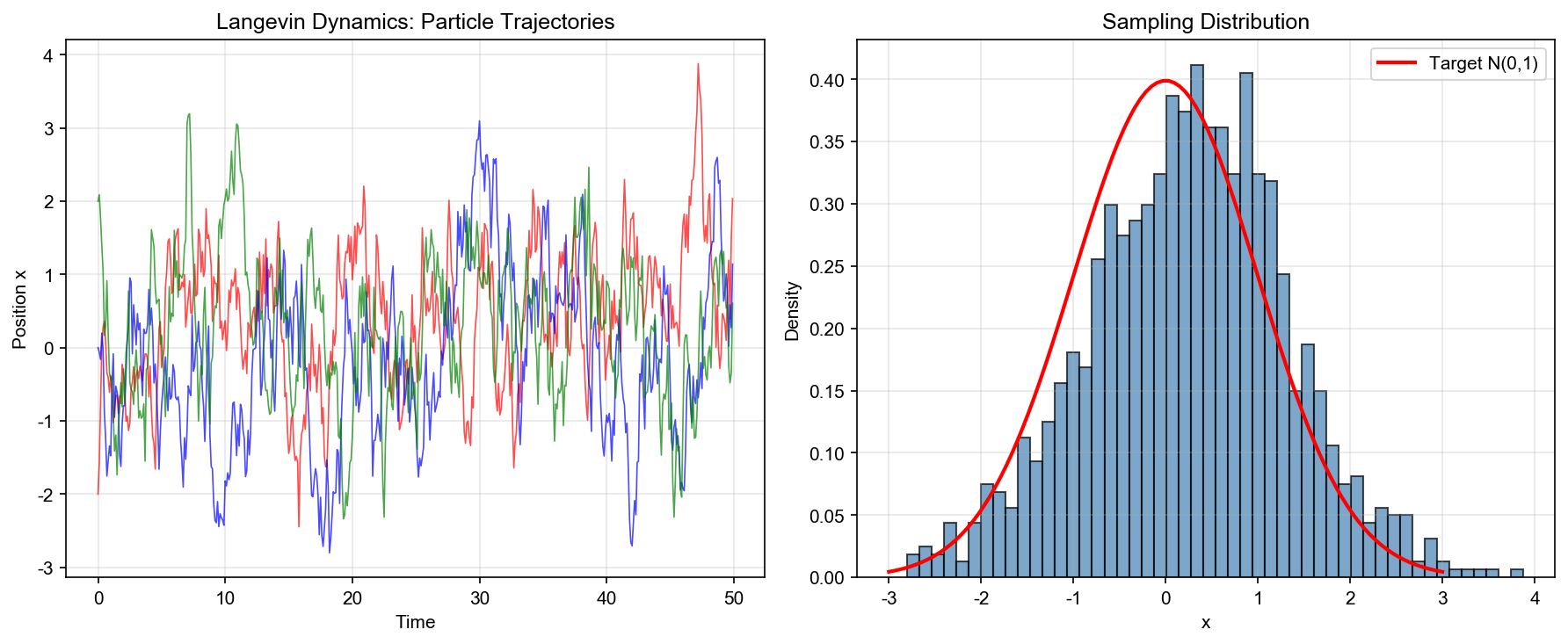
预期结果： - 初始分布集中在附近 - 随时间演化，分布逐渐扩散并移动到双峰位置 - 最终收敛到平衡分布（双峰结构）

实验 2： Langevin 动力学采样（多峰分布）

目标：用 Langevin 动力学从多峰分布中采样，比较不同温度参数的效果。

设置： - 目标分布：，其中 - 采样方法： Euler-Maruyama 离散化 - 温度参数：完整代码见 experiment2_langevin_sampling.py。

关键步骤： 1. 初始化： 1000 个粒子，初始位置集中在原点附近 2. Langevin 更新：使用 Euler-Maruyama 方法，步长 3. 预热期：前 1000 步作为预热期，不用于统计 4. 可视化：比较不同温度参数下的采样分布，以及单个粒子的轨迹

预期结果： - 低温度（大）：采样更集中在峰值附近 - 高温度（小）：采样更分散，能更好地探索整个分布 - 所有情况下，采样分布都应接近真实分布

实验 3： VI vs MCMC 收敛性对比

目标：比较变分推断和 Langevin MCMC 的收敛速度。

设置： - 目标分布：，其中 - 变分推断：使用高斯分布 - MCMC： Langevin 动力学

完整代码见 experiment3_vi_vs_mcmc.py。

关键步骤： 1. 变分推断：使用 Adam 优化器最小化 KL 散度，参数为 2. Langevin MCMC：使用 100 个粒子进行采样，每 10 步计算一次 KL 散度 3. KL 散度计算： VI 使用蒙特卡洛估计， MCMC 使用 KDE 估计经验分布 4. 可视化：对比两种方法的收敛速度和最终分布

预期结果： - 变分推断：快速收敛（但可能有近似误差） - MCMC：较慢收敛（但渐近精确）

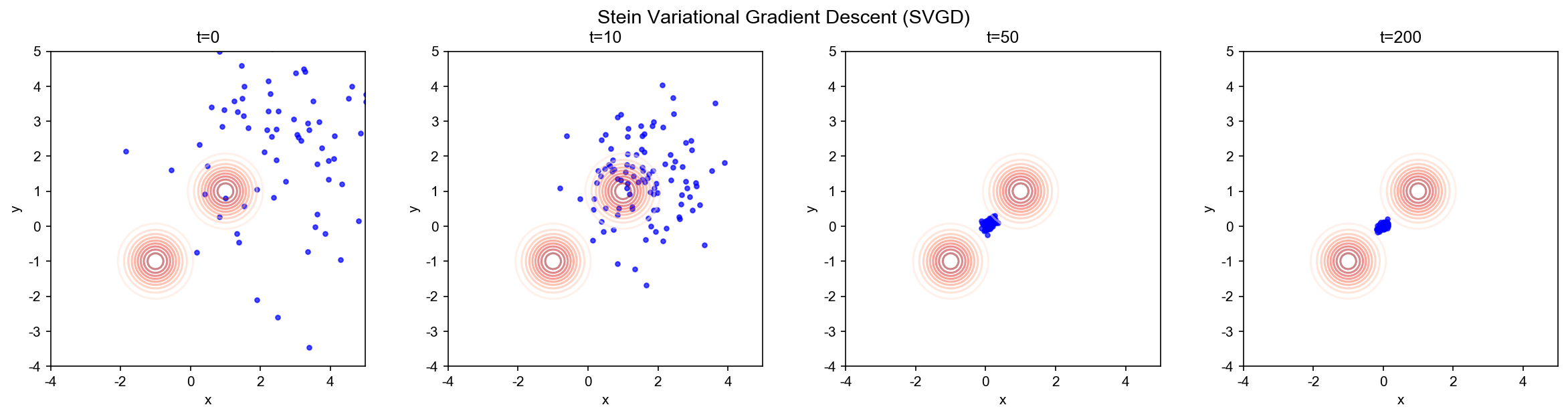
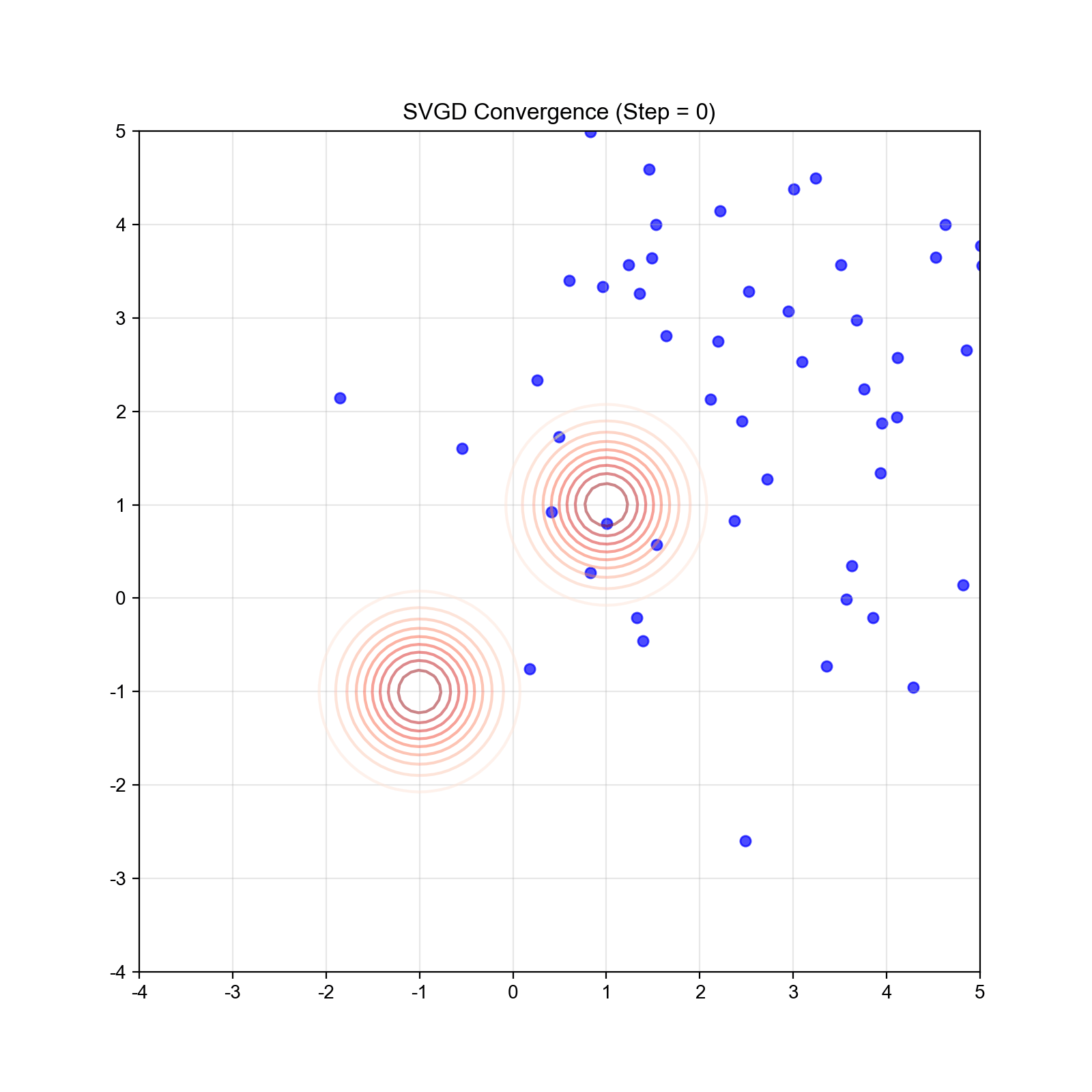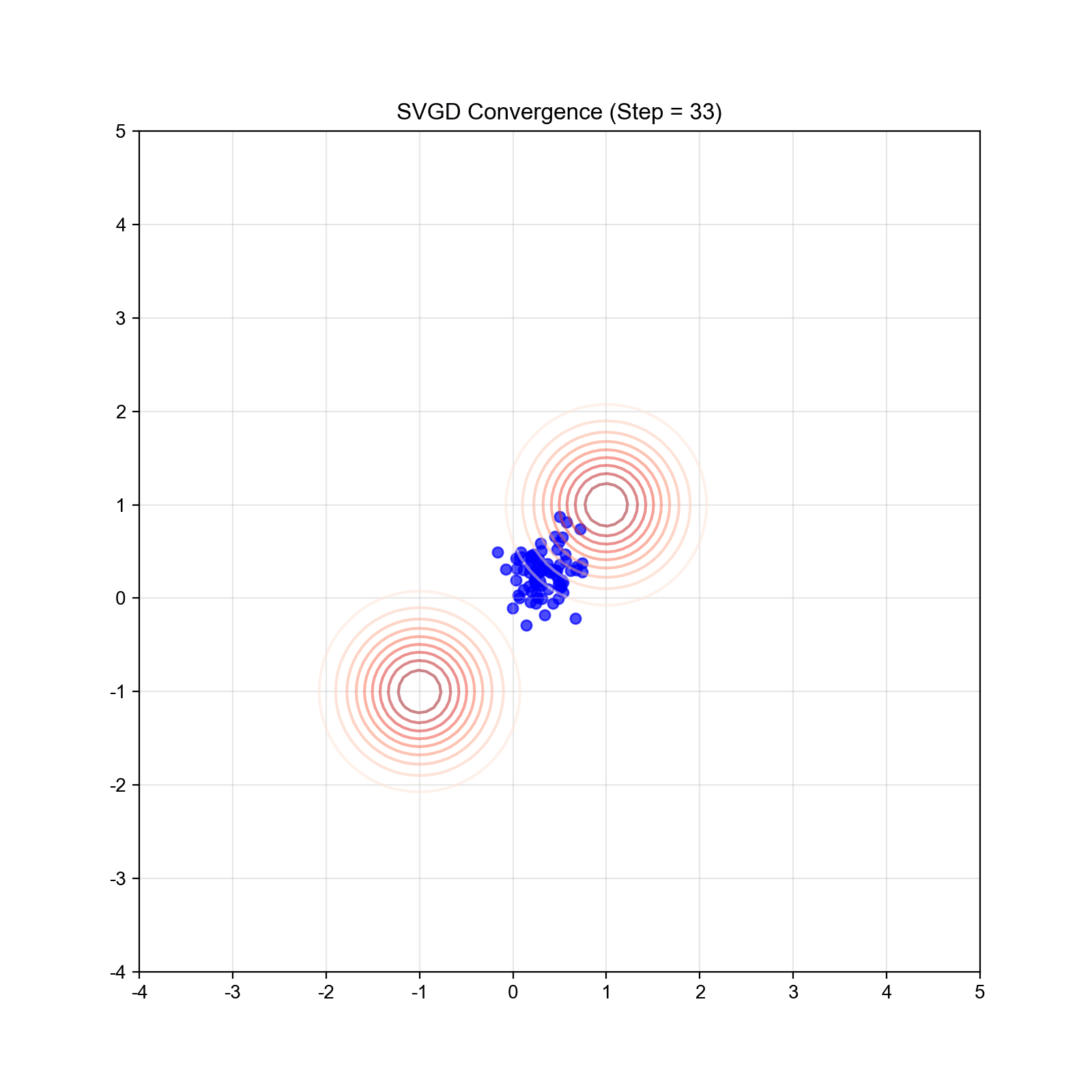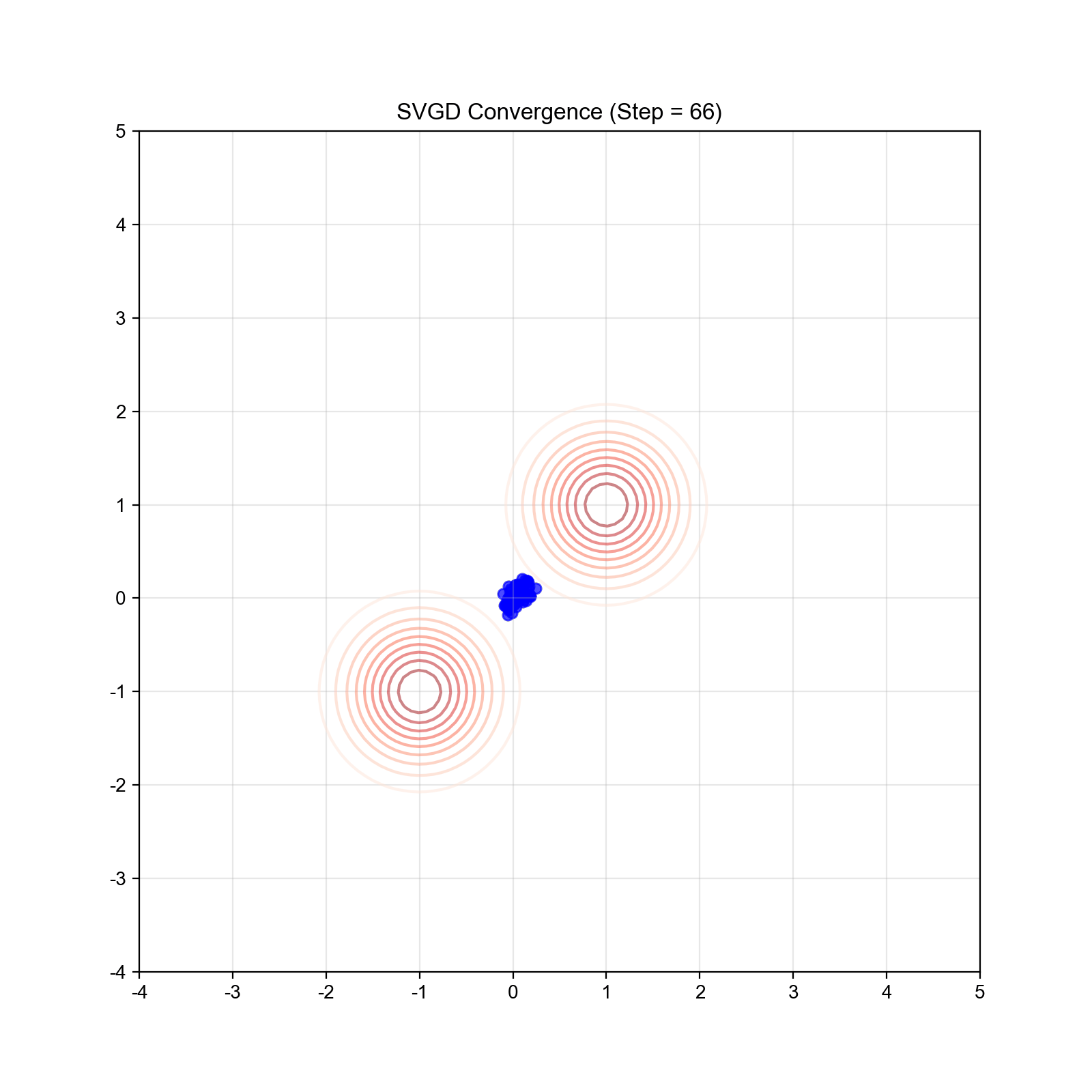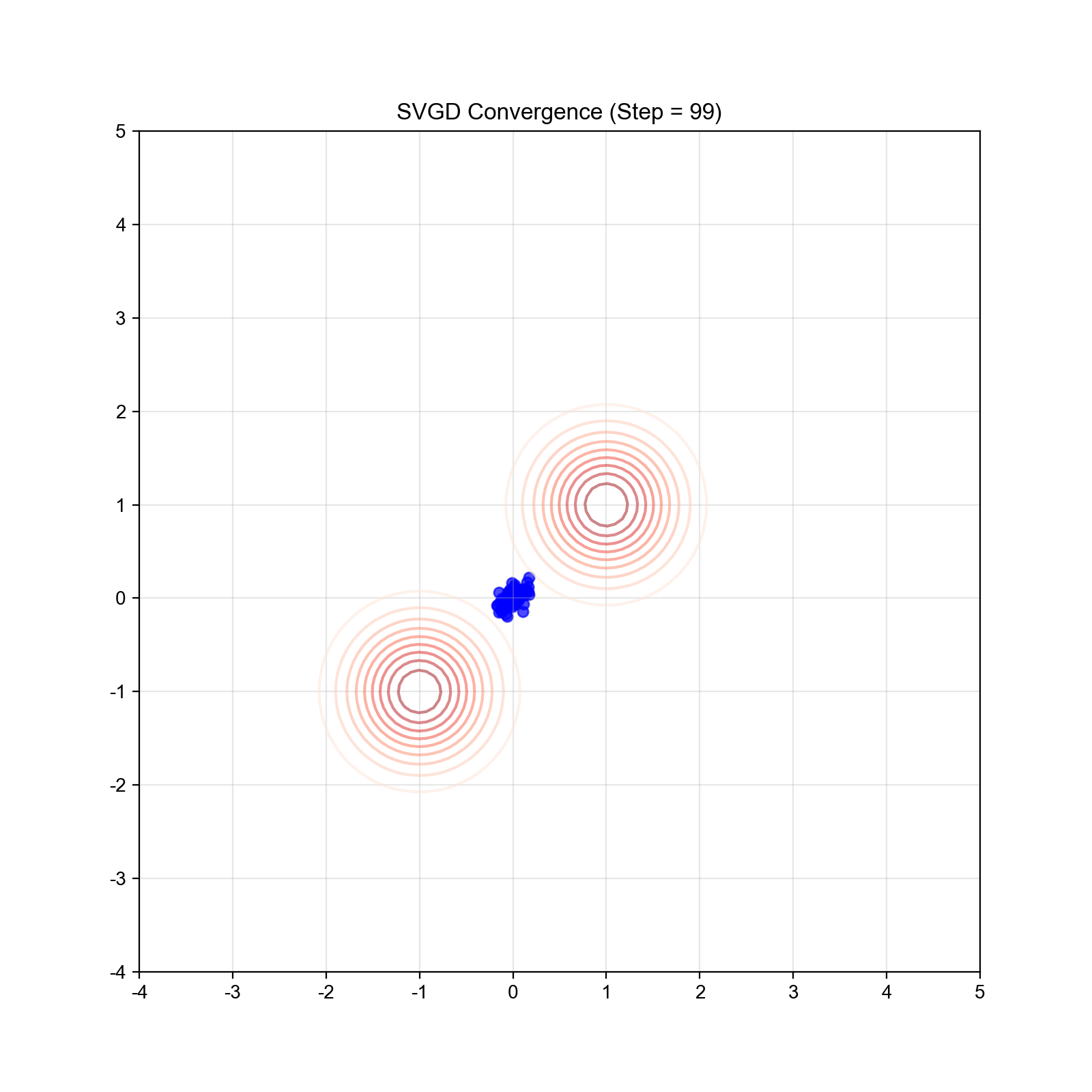
实验 4： SVGD 粒子轨迹与密度估计

目标：可视化 SVGD 的粒子演化过程，展示粒子如何分散到目标分布的不同模式。

设置： - 目标分布：，其中（双峰） - 初始粒子：集中在附近 - 核函数： RBF 核，带宽完整代码见 experiment4_svgd.py。

关键步骤： 1. 初始化： 100 个粒子，初始位置集中在原点附近 2. SVGD 更新：使用 RBF 核函数，步长 3. 可视化：展示粒子分布演化、粒子轨迹、粒子间距离变化，以及 KL 散度收敛

预期结果： - 初始：粒子集中在附近 - 演化过程中：粒子逐渐分散到两个峰值 - 最终：粒子分布接近目标分布（双峰结构）

系列总结： PDE 与机器学习的统一视角

经过八篇文章的系统性探索，我们建立了从偏微分方程视角理解机器学习的完整理论框架。让我们回顾这一系列的核心思想：

核心主题回顾

变分原理与神经网络优化：将神经网络训练视为 Wasserstein 空间中的梯度流，揭示了优化过程的连续动力学本质。
物理信息神经网络：将 PDE 求解问题转化为优化问题，展示了深度学习方法在科学计算中的应用。
神经算子理论：学习无限维映射，统一了函数空间上的学习问题。
扩散模型的 PDE 本质：揭示了生成模型的数学基础，建立了 SDE 、 Fokker-Planck 方程与 Score Matching 的联系。
连续归一化流：将流模型与常微分方程联系起来，提供了生成模型的另一种视角。
反应扩散系统与图神经网络：揭示了 GNN 的过度平滑问题，反应扩散方程提供解决之道。
辛几何与保结构神经网络：让神经网络尊重物理守恒律，实现长时间准确预测。
变分推断的 PDE 理论：统一了变分推断与 MCMC 方法，展示了概率推断的连续时间动力学。

统一的数学框架

所有这些主题都围绕一个核心思想：机器学习问题可以视为偏微分方程的求解问题。

优化问题 → Wasserstein 梯度流
采样问题 → Fokker-Planck 方程
函数学习 → 算子方程
生成模型 → 扩散方程

未来方向

更复杂的 PDE 结构：探索分数阶 PDE 、随机 PDE 等在机器学习中的应用。
数值方法的改进：将经典 PDE 数值方法（有限元、谱方法）应用到机器学习中。
理论分析：建立更严格的收敛性、稳定性理论。
实际应用：将 PDE 视角应用到实际问题中，如科学计算、金融建模等。

结语

偏微分方程与机器学习的交叉领域正在快速发展。通过这一系列文章，我们希望读者能够：

理解数学本质：从 PDE 视角深入理解机器学习的理论基础
掌握实用工具：学会用 PDE 方法解决实际问题
探索前沿方向：了解当前研究热点和未来发展方向

数学的美在于统一性。当我们用偏微分方程的语言重新审视机器学习时，看似不同的方法展现出深刻的联系。这种统一性不仅加深了我们的理解，也为设计新算法提供了强大的工具。

✅ 小白检查点（第 8 篇）

学完这篇文章，建议理解以下核心概念：

核心概念回顾

1. 变分推断（ VI）是什么 - 简单说：用简单分布（如高斯）近似复杂的后验分布 - 生活类比：用圆形近似不规则图形（虽然不完全准确，但计算简单） - 数学：最小化，找到最接近真实分布的简单分布 2. MCMC 是什么 - 简单说：通过随机游走生成服从目标分布的样本 - 生活类比：想知道城市人口分布，随机在街上走，记录遇到的人 - 优势：理论上能准确采样，劣势：慢（需要很多步才能"遍历"整个空间）

3. Fokker-Planck 方程的作用 - 简单说：描述概率密度如何随时间演化的 PDE - 与 SDE 的关系： - SDE：描述单个粒子如何随机运动 - Fokker-Planck：描述大量粒子的密度分布如何演化 - 应用：分析 Langevin 动力学是否收敛到目标分布

4. Langevin 动力学 - 简单说：带热噪声的梯度下降，用于采样 - 公式： - 漂移项：（朝高概率区域走） - 扩散项：（热噪声，防止卡在局部） - 为什么收敛： Fokker-Planck 方程的稳态解正是目标分布 5. 过阻尼 vs 欠阻尼 Langevin - 过阻尼（ 1 阶）： - 类比：在蜂蜜中移动（阻力大，速度立即响应力） - 适用：高维空间，计算简单

欠阻尼（ 2 阶）：引入动量

dX_t = v_t dt, dv_t = -v_t dt + p(X_t) dt + dW_t $$

类比：有惯性的运动（可以"冲过"局部障碍）
适用：多峰分布，能更快穿越低概率区域

6. KL 散度的梯度流解释 - 简单说： VI 可以看成在 Wasserstein 空间中沿 KL 散度下降 - 连续时间 VI： - 物理意义：概率质量从高但低的区域流向高的区域

7. SVGD（ Stein 变分梯度下降） - 简单说：用有限个粒子近似分布，粒子之间相互作用 - 关键： - 每个粒子不是独立采样 - 粒子之间通过核函数相互推斥（防止聚集） - 优势：比 MCMC 快（不需要 burn-in），比 VI 准（用粒子表示，不限制分布族）

8. It ô vs Stratonovich 积分 - It ô积分：标准的随机积分，用于金融、物理 - 特点：噪声与当前状态"独立" - 链式法则需要修正（ It ô引理）

Stratonovich 积分：物理上更自然的随机积分
- 特点：噪声作用在"区间中点"
- 链式法则不需要修正（像普通微积分）

一句话记忆

"变分推断 = 优化问题， MCMC = 采样问题，两者通过 Fokker-Planck 方程统一"

"Langevin 动力学 = 梯度 + 噪声，长时间后收敛到目标分布"

常见误解澄清

误解 1："VI 总是比 MCMC 快" - 澄清：通常是，但不绝对 - VI 优势：快（优化问题），但可能不准（受限于分布族） - MCMC 优势：准（理论保证），但慢（需要大量样本） - 选择：快速近似 → VI；高精度 → MCMC

误解 2："Langevin 动力学就是加了噪声的梯度下降" - 澄清：目标不同！ - 梯度下降：找最优点（最小化目标函数） - Langevin 动力学：采样（生成服从分布的样本） - 关键区别： Langevin 需要噪声来"探索"整个分布，而非收敛到单个点

误解 3："SVGD 只是粒子系统" - 澄清：有深刻的 Stein 理论基础 - Stein 算子： - Stein 恒等式：（特征性质） - SVGD：在 Stein 算子诱导的空间中做梯度下降

误解 4："过阻尼 Langevin 一定比欠阻尼好" - 澄清：取决于分布形状 - 单峰、光滑 → 过阻尼足够（简单快速） - 多峰、复杂 → 欠阻尼更好（惯性帮助跨越势垒） - 实践：先试过阻尼，如果混合慢再用欠阻尼

误解 5："Fokker-Planck 方程只是理论工具" - 澄清：有实际应用！ - 分析采样算法的收敛速度 - 设计新的采样方法（如加速版 Langevin） - 在连续归一化流中计算密度

如果只记住三件事

变分推断的本质：用优化问题近似采样问题，快但可能不够准（受限于分布族 $Missing superscript or subscript argument q_$ ）
Langevin 动力学的核心：（梯度）+ 噪声（探索），长时间后收敛到（由 Fokker-Planck 方程保证）
PDE 统一视角：
- VI → KL 散度的梯度流（ PDE）
- MCMC → Fokker-Planck 方程的稳态
- 两者都是概率密度的动力学系统

✅ 系列总小白检查点（ 8 篇文章）

恭喜你完成了"PDE 与机器学习"系列的学习！让我们用最简单的语言回顾整个系列：

八篇文章的核心思想

变分原理：优化是在"函数空间"中找最优函数，神经网络训练是概率分布的"流动"
PINN：把 PDE 当成损失函数，用神经网络"猜答案"
神经算子：学习函数→函数的映射，一次训练处理所有参数
扩散模型：前向加噪（热扩散），反向去噪（时间倒流）
神经 ODE：深度网络是 ODE 的离散化，伴随方法省内存
反应扩散与 GNN：扩散让节点变相似（过度平滑），反应保持差异
辛几何：让神经网络尊重物理守恒律（能量、动量）
变分推断： VI（优化）和 MCMC（采样）通过 Fokker-Planck 方程统一

最核心的统一思想

机器学习的很多问题，本质上都是在解偏微分方程（ PDE）

训练神经网络 = 解梯度流方程
生成样本 = 解扩散方程
推断分布 = 解 Fokker-Planck 方程
学习物理规律 = 解守恒律方程

为什么 PDE 视角重要？

理论洞察：理解为什么算法工作（收敛性、稳定性）
算法设计：借鉴 PDE 数值方法设计新算法
性能保证：通过 PDE 理论分析预测算法行为

感谢你的耐心学习！希望这个系列让你对机器学习有了更深的数学理解。

参考文献

Langevin Diffusion Variational Inference. arXiv:2208.07743
Variational Inference as Parametric Langevin Dynamics. ICML 2020
Fokker-Planck Transport. arXiv:2410.18993
Stein Variational Gradient Descent: A General Purpose Bayesian Inference Algorithm. arXiv:1608.04471
Blei, D. M., Kucukelbir, A., & McAuliffe, J. D. (2017). Variational Inference: A Review for Statisticians. Journal of the American Statistical Association, 112(518), 859-877.
Ambrosio, L., Gigli, N., & Savar é, G. (2008). Gradient Flows: In Metric Spaces and in the Space of Probability Measures. Birkh ä user.
Villani, C. (2009). Optimal Transport: Old and New. Springer.