LeetCode（四）—— 滑动窗口技巧

滑动窗口是解决数组和字符串问题的一把利器。当你遇到"子数组"、"子串"、"连续"这些关键词时，滑动窗口往往能提供 时间复杂度的优雅解法。这篇文章会从基础概念开始，逐步深入到固定窗口和可变窗口两种模式，并通过多道 LeetCode 经典题目帮你彻底掌握这个技巧。

什么是滑动窗口

滑动窗口（ Sliding Window）是一种双指针技巧的变体，主要用于解决数组或字符串中的连续子区间问题。它维护一个窗口，通过移动窗口的左右边界来遍历所有可能的子区间，同时利用窗口内的信息避免重复计算。

想象一下，你在一列火车上，透过一个固定大小的窗户看外面的风景。随着火车前进，窗户会"滑动"到新的位置，但窗户的大小保持不变。这就是固定窗口大小的情况。另一种情况是，窗户的大小可以变化——可以拉大或缩小窗户，直到看到最合适的风景。这就是可变窗口大小的情况。

在算法中，滑动窗口通常涉及两个指针（ left 和 right）：

• 左指针（ left）：窗口的左边界
• 右指针（ right）：窗口的右边界
• 窗口： left 和 right 之间的区间

通过移动这两个指针，可以：

1. 扩大窗口：移动 right 指针
2. 缩小窗口：移动 left 指针
3. 保持窗口大小：同时移动 left 和 right

滑动窗口的核心思想

滑动窗口本质上是一种双指针技术，通过维护一个"窗口"（即左右两个指针之间的区间）来解决子数组/子串问题。它的核心优势在于：避免重复计算。

思路演进：从暴力到优化

❌ 方法一：暴力枚举（超时）

直觉：对于求"最长/最短子串"问题，最简单的想法是枚举所有可能的子串，检查每个子串是否满足条件。

为什么不行： - 时间复杂度： 或 （枚举起点和终点 + 检查条件） - 问题：大量重复计算——每次移动起点时，前面已经检查过的部分又重新检查一遍

示例（无重复字符的最长子串）：

# 暴力解法示例
def lengthOfLongestSubstring_brute(s: str) -> int:
    n = len(s)
    max_len = 0
    
    # 枚举所有可能的起点
    for i in range(n):
        # 枚举所有可能的终点
        for j in range(i, n):
            # 检查 s[i:j+1] 是否无重复字符
            substring = s[i:j+1]
            if len(substring) == len(set(substring)):
                max_len = max(max_len, j - i + 1)
            else:
                break  # 剪枝：遇到重复就停止
    
    return max_len

复杂度： - 时间： （双重循环）到 （如果不剪枝，每次还要检查整个子串） - 空间： （ set 存储字符）

✅ 方法二：滑动窗口（最优）

优化思路：利用"窗口滑动"避免重复计算。关键洞察是：

1. 窗口扩展：右指针向右移动，尝试扩大窗口
2. 窗口收缩：当窗口内不满足条件时，左指针向右移动，缩小窗口
3. 增量更新：每次只处理新加入/移出的元素，不重新检查整个窗口

为什么有效： - 每个元素最多被访问两次（一次被右指针加入，一次被左指针移出） - 时间复杂度： - 避免了暴力法的重复计算

关键洞察： - 单调性：如果 [left, right] 不满足条件，那么 [left, right+1]、[left, right+2] 等也不会满足（对于某些问题） - 贪心策略：在保证条件的前提下，尽量扩大窗口（求最长），或尽量缩小窗口（求最短）

火车车厢类比

想象你在查看一列火车的车厢：

• 暴力法：每次重新数一遍所有车厢（从头开始检查）
• 滑动窗口：
  • 右边新车厢进入时：只检查新车厢是否符合条件
  • 左边车厢驶离时：只移除最左边的车厢
  • 无需重新检查中间的车厢

可视化示例（无重复字符的最长子串）：

字符串："abcabcbb"
目标：找出最长无重复字符子串

初始状态：
┌─┐
│ a │ b  c  a  b  c  b  b
└─┘
left=0, right=0, 窗口="a", 无重复 ✓

步骤 1： right 向右扩展
┌───────┐
│ a  b  c │ a  b  c  b  b
└───────┘
left=0, right=2, 窗口="abc", 无重复 ✓, max_len=3

步骤 2： right 继续扩展，遇到重复'a'
┌───────────┐
│ a  b  c  a │ b  c  b  b
└───────────┘
left=0, right=3, 窗口="abca", 有重复 ✗

步骤 3： left 收缩，移除重复的'a'
      ┌───────┐
   a │ b  c  a │ b  c  b  b
      └───────┘
left=1, right=3, 窗口="bca", 无重复 ✓

最终： max_len=3（"abc"）

滑动窗口的高效性来源

滑动窗口之所以高效，是因为它利用了问题的两个关键特性：

重复子问题（增量更新）

当我们计算窗口 [left, right] 的信息时，窗口 [left+1, right+1] 的信息可以通过增量更新的方式得到，而不需要重新计算整个窗口。

例子：计算窗口内元素的和

# 暴力法：每次重新计算整个窗口的和 O(n^2)
window_sum = sum(arr[left:right+1])

# 滑动窗口：增量更新 O(1)
window_sum = window_sum - arr[left] + arr[right+1]

单调性（决定窗口移动策略）

在很多问题中，窗口的某些性质（如和、最大值、字符种类数等）会随着窗口的扩大或缩小呈现单调性。例如：

• 窗口越大，和越大（非负数组）
• 窗口越大，包含的字符种类越多
• 窗口越大，最大值不会变小（非严格单调）

利用这些特性，可以用 的时间复杂度解决原本需要 或更高复杂度的问题。

固定窗口大小问题

固定窗口大小的问题相对简单，因为窗口的大小是预先确定的。我们只需要维护一个固定大小的窗口，在数组上滑动，并记录每个窗口的某些属性（如和、最大值、平均值等）。

模板代码

def fixed_window(nums, k):
    """
    固定窗口大小为 k 的模板
    """
    n = len(nums)
    if n < k:
        return []
  
    # 初始化窗口 [0, k-1]
    window_sum = sum(nums[:k])
    result = [window_sum]
  
    # 滑动窗口
    for i in range(k, n):
        # 移除左边界元素，加入右边界元素
        window_sum = window_sum - nums[i - k] + nums[i]
        result.append(window_sum)
  
    return result

例题：子数组最大平均值

LeetCode 643. 子数组最大平均值

给定一个整数数组 nums 和一个整数 k，找出长度为 k 的连续子数组的最大平均值。

示例：

输入: nums = [1,12,-5,-6,50,3], k = 4
输出: 12.75
解释: 最大平均值 (12-5-6+50)/4 = 51/4 = 12.75

思路：

1. 维护一个大小为 k 的窗口
2. 计算每个窗口的平均值
3. 返回最大值

Python 实现：

def findMaxAverage(nums, k):
    n = len(nums)
    # 计算第一个窗口的和
    window_sum = sum(nums[:k])
    max_sum = window_sum
  
    # 滑动窗口
    for i in range(k, n):
        window_sum = window_sum - nums[i - k] + nums[i]
        max_sum = max(max_sum, window_sum)
  
    return max_sum / k

Java 实现：

public double findMaxAverage(int[] nums, int k) {
    int n = nums.length;
    int windowSum = 0;
  
    // 计算第一个窗口的和
    for (int i = 0; i < k; i++) {
        windowSum += nums[i];
    }
  
    int maxSum = windowSum;
  
    // 滑动窗口
    for (int i = k; i < n; i++) {
        windowSum = windowSum - nums[i - k] + nums[i];
        maxSum = Math.max(maxSum, windowSum);
    }
  
    return (double) maxSum / k;
}

时间复杂度：，每个元素最多被访问两次（一次加入窗口，一次移出窗口） 空间复杂度：，只使用了常数额外空间

例题：大小为 K 且平均值大于等于阈值的子数组数目

LeetCode 1343. 大小为 K 且平均值大于等于阈值的子数组数目

给你一个整数数组 arr 和两个整数 k 和 threshold，返回长度为 k 且平均值大于等于 threshold 的子数组数目。

示例：

输入: arr = [2,2,2,2,5,5,5,8], k = 3, threshold = 4
输出: 3
解释: 子数组 [2,5,5],[5,5,5] 和 [5,5,8] 的平均值分别为 4, 5 和 6 。

思路：

1. 维护大小为 k 的窗口
2. 计算每个窗口的和
3. 如果窗口和 >= threshold * k，计数加一

Python 实现：

def numOfSubarrays(arr, k, threshold):
    n = len(arr)
    window_sum = sum(arr[:k])
    count = 1 if window_sum >= k * threshold else 0
  
    for i in range(k, n):
        window_sum = window_sum - arr[i - k] + arr[i]
        if window_sum >= k * threshold:
            count += 1
  
    return count

可变窗口大小问题

可变窗口大小的问题更加灵活，窗口的大小会根据问题的约束条件动态调整。这类问题通常需要找到满足某种条件的最长或最短子数组/子串。

窗口收缩条件详解

窗口收缩（左指针右移）是滑动窗口最关键的部分，决定了算法的正确性。什么时候收缩和收缩到什么程度是两个核心问题。

核心原则：当窗口不满足条件时，必须收缩直到重新满足条件。

收缩时机：三种典型场景

场景一：窗口违反约束（求最长）

特征：窗口内某个指标超过了限制 - 无重复字符：窗口内出现重复字符 - 最多 k 个不同字符：窗口内不同字符数 > k - 和不超过 target：窗口和 > target

收缩策略：移动 left 直到窗口重新满足约束

# 示例：无重复字符的最长子串
while right 指向的字符在窗口中已存在:
    移除 left 指向的字符
    left += 1

为什么这样收缩？因为当前窗口 [left, right] 不满足条件，那么任何包含这个窗口的更大窗口（如 [left, right+1]）也不会满足条件。所以必须缩小左边界。

场景二：窗口满足条件（求最短）

特征：窗口已经满足了目标条件 - 最小覆盖子串：窗口包含了所有目标字符 - 和 >= target：窗口和已经 >= target

收缩策略：尽可能缩小窗口，在保持满足条件的前提下

# 示例：最小覆盖子串
while 窗口仍然包含所有目标字符:
    更新最小长度
    移除 left 指向的字符
    left += 1

为什么这样收缩？因为题目要求最短/最小，所以在满足条件后，要尽可能缩小窗口，找到最小的满足条件的窗口。

场景三：固定窗口大小

特征：窗口大小固定为 k - 大小为 k 的子数组最大和 - 长度为 k 的子串出现次数

收缩策略：每次右指针移动时，左指针也移动（保持窗口大小 = k）

# 示例：大小为 k 的子数组最大和
if right - left + 1 == k:
    更新答案
    left += 1  # 保持窗口大小

收缩条件对比表

问题类型	收缩时机	收缩条件	示例
求最长	窗口违反约束时	while 不满足条件	无重复字符的最长子串
求最短	窗口满足条件时	while 满足条件	最小覆盖子串
固定大小	窗口达到 k 时	if size == k	大小为 k 的子数组最大和

窗口收缩的数学证明

为什么求最长时，遇到违反约束就收缩？

反证法：假设窗口 [left, right] 不满足条件，但存在一个更长的满足条件的窗口 [left, right+k]（ k > 0）。 - 因为 [left, right] 不满足条件，而 [left, right+k] 是 [left, right] 的超集 - 如果条件是"单调递增的"（如元素数量、字符种类数），那么 [left, right+k] 也不会满足条件 - 矛盾！所以不存在这样的窗口

结论：当窗口不满足条件时，必须收缩左边界，不能继续扩大右边界。

为什么求最短时，满足条件后仍要收缩？

贪心思想：当前窗口 [left, right] 满足条件，但可能不是最短的。尝试缩小左边界： - 如果缩小后仍满足条件：说明左边界的元素是"多余的"，可以继续缩小 - 如果缩小后不满足条件：说明当前窗口是以 right 为右边界的最短窗口

结论：在满足条件的前提下，尽可能缩小窗口，才能找到最短的。

两种常见模式

模式一：寻找最长子串/子数组（窗口违反约束时收缩）

这类问题的目标是找到满足条件的最长子串。通常的做法是：

1. 扩展窗口：不断扩大窗口（移动 right）
2. 收缩窗口：当窗口不满足条件时，缩小窗口（移动 left）
3. 更新答案：在窗口满足条件时，更新最大长度

模板代码：

def max_length_template(arr):
    left = 0
    max_len = 0
    # window_state 用于维护窗口的状态（如哈希表、计数器等）
    window_state = {}
    
    for right in range(len(arr)):
        # 将 arr[right] 加入窗口
        update_window_state(arr[right], window_state)
        
        # 收缩窗口：当窗口不满足条件时
        while not is_valid(window_state):
            # 移除 arr[left]
            remove_from_window(arr[left], window_state)
            left += 1
        
        # 更新答案：此时窗口满足条件
        max_len = max(max_len, right - left + 1)
    
    return max_len

关键点： - 收缩条件：while not is_valid(window_state)（窗口不满足条件） - 更新答案：在收缩后（窗口满足条件）

模式二：寻找最短子串/子数组（窗口满足条件时收缩）

这类问题的目标是找到满足条件的最短子串。通常的做法是：

1. 扩展窗口：不断扩大窗口（移动 right），直到满足条件
2. 收缩窗口：一旦满足条件，尝试缩小窗口（移动 left），在保持满足条件的前提下寻找更短的解
3. 更新答案：在窗口满足条件时，更新最小长度

模板代码：

def min_length_template(arr, target):
    left = 0
    min_len = float('inf')  # 初始化为无穷大
    window_state = {}
    
    for right in range(len(arr)):
        # 将 arr[right] 加入窗口
        update_window_state(arr[right], window_state)
        
        # 收缩窗口：当窗口满足条件时
        while is_valid(window_state, target):
            # 更新答案：此时窗口满足条件，尝试更新最小长度
            min_len = min(min_len, right - left + 1)
            
            # 移除 arr[left]，尝试缩小窗口
            remove_from_window(arr[left], window_state)
            left += 1
    
    return min_len if min_len != float('inf') else 0

关键点： - 收缩条件：while is_valid(window_state, target)（窗口满足条件） - 更新答案：在收缩前（窗口满足条件时）

对比：最长 vs 最短

特性	求最长	求最短
收缩时机	窗口不满足条件时	窗口满足条件时
收缩目的	恢复满足条件	寻找更短的满足条件的窗口
更新答案	收缩后（窗口满足条件）	收缩前（窗口满足条件）
初始值	max_len = 0	min_len = inf
典型问题	无重复字符的最长子串	最小覆盖子串

模板代码（通用）

def sliding_window_template(s):
    """
    可变窗口大小的通用模板
    
    适用场景：
    1. 求最长子串/子数组（窗口不满足条件时收缩）
    2. 求最短子串/子数组（窗口满足条件时收缩）
    """
    left = 0
    result = 0  # 或 result = []
  
    # 用于记录窗口状态的变量
    window = {}  # 或 window = []
  
    for right in range(len(s)):
        # 扩大窗口：加入 s[right]
        window[s[right]] = window.get(s[right], 0) + 1
      
        # 判断窗口是否需要收缩
        while window_needs_shrink(window):
            # 缩小窗口：移除 s[left]
            window[s[left]] -= 1
            if window[s[left]] == 0:
                del window[s[left]]
            left += 1
      
        # 更新答案
        result = update_result(result, left, right)
  
    return result

经典题目详解

题目一：无重复字符的最长子串

LeetCode 3. 无重复字符的最长子串

给定一个字符串 s，请你找出其中不含有重复字符的最长子串的长度。

示例：

输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3 。

思路分析：

这是一个典型的"寻找最长子串"问题。需要：

1. 维护一个窗口，窗口内的字符都不重复
2. 用哈希表记录窗口中每个字符的出现次数
3. 当窗口中出现重复字符时，缩小窗口（移动 left），直到没有重复字符
4. 在窗口没有重复字符时，更新最长长度

详细步骤：

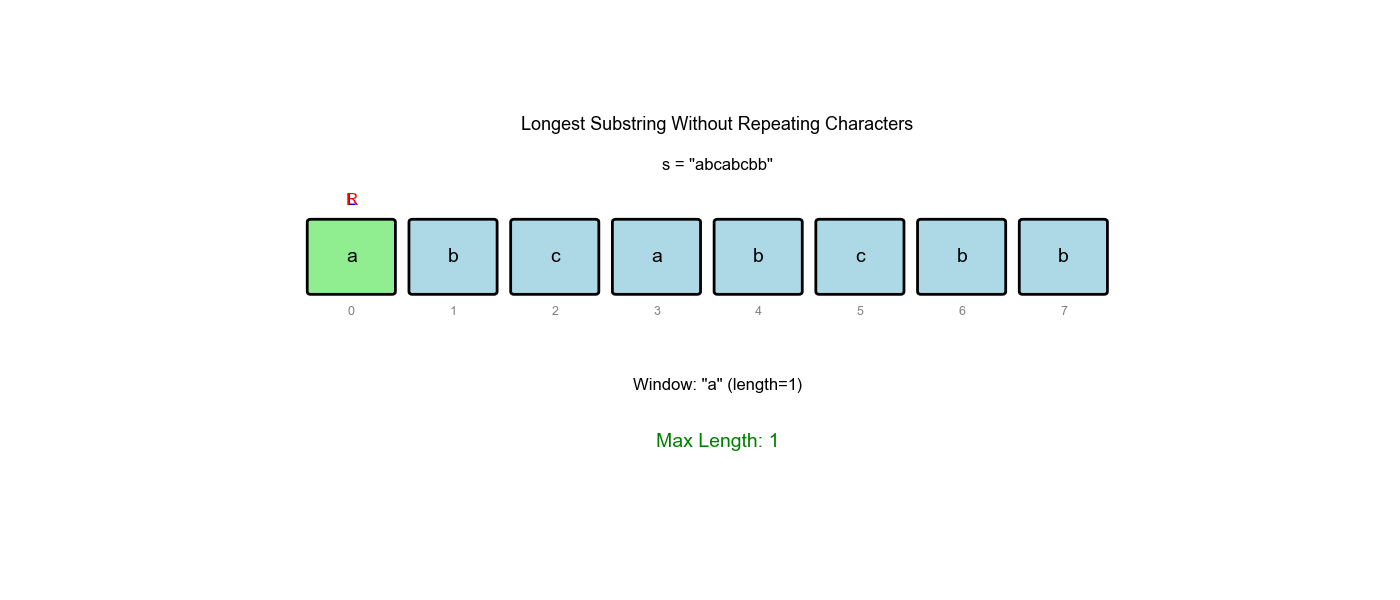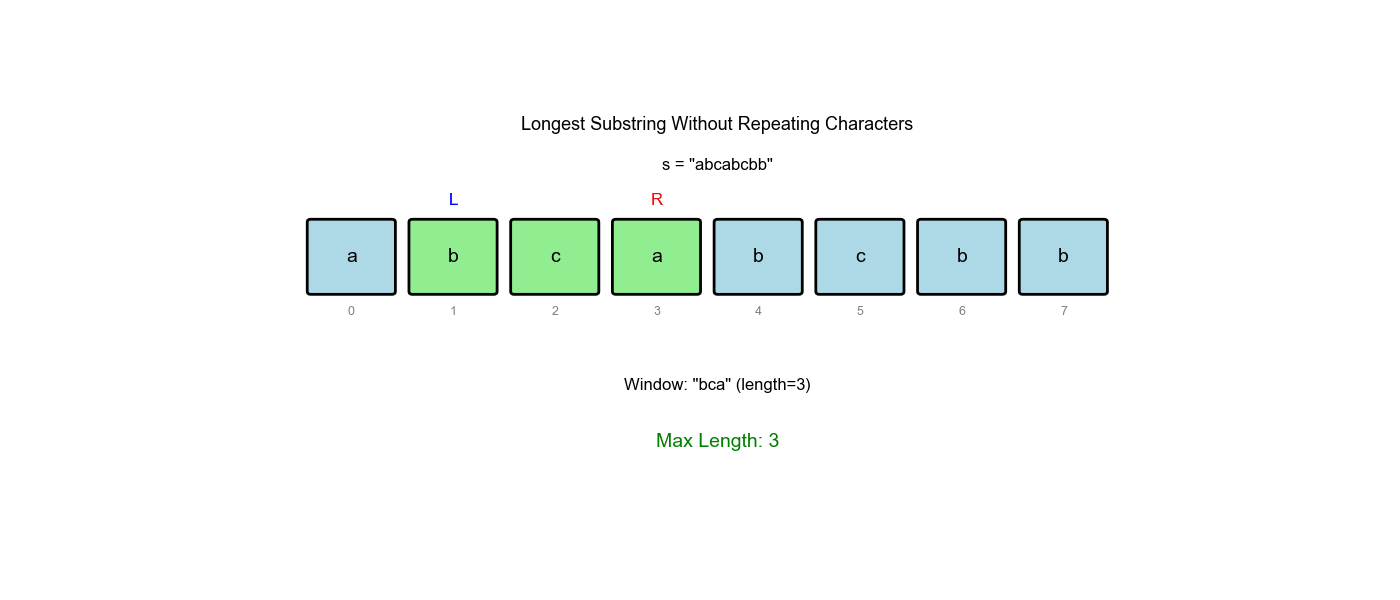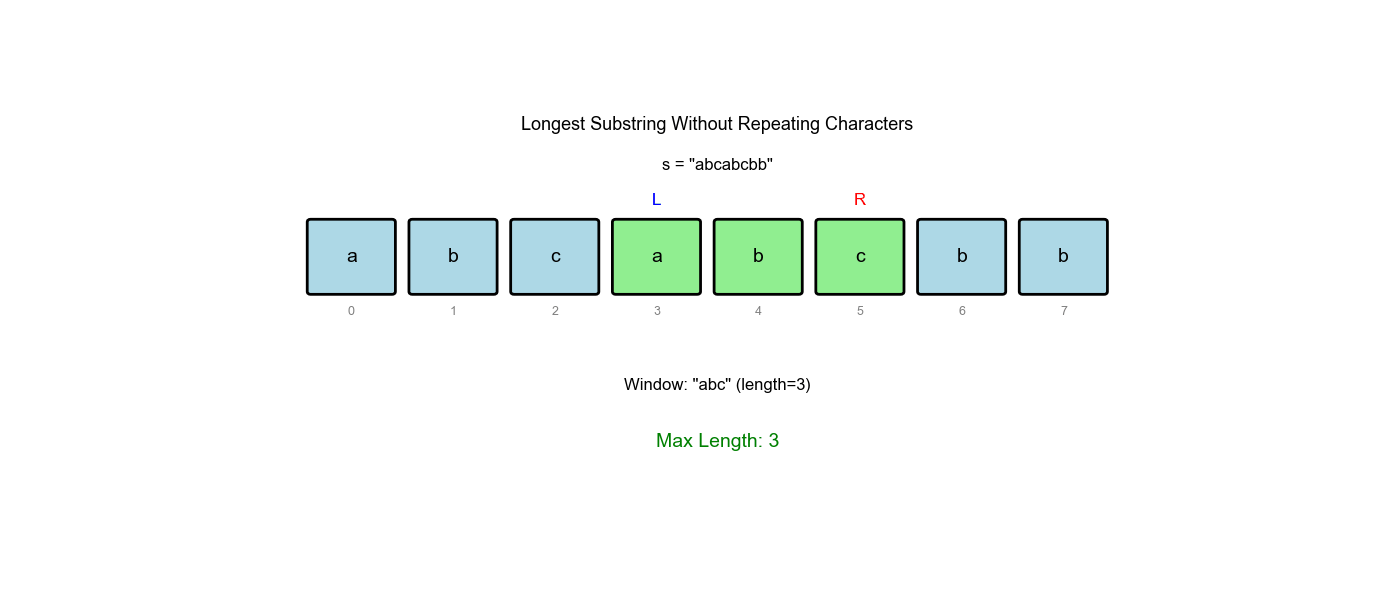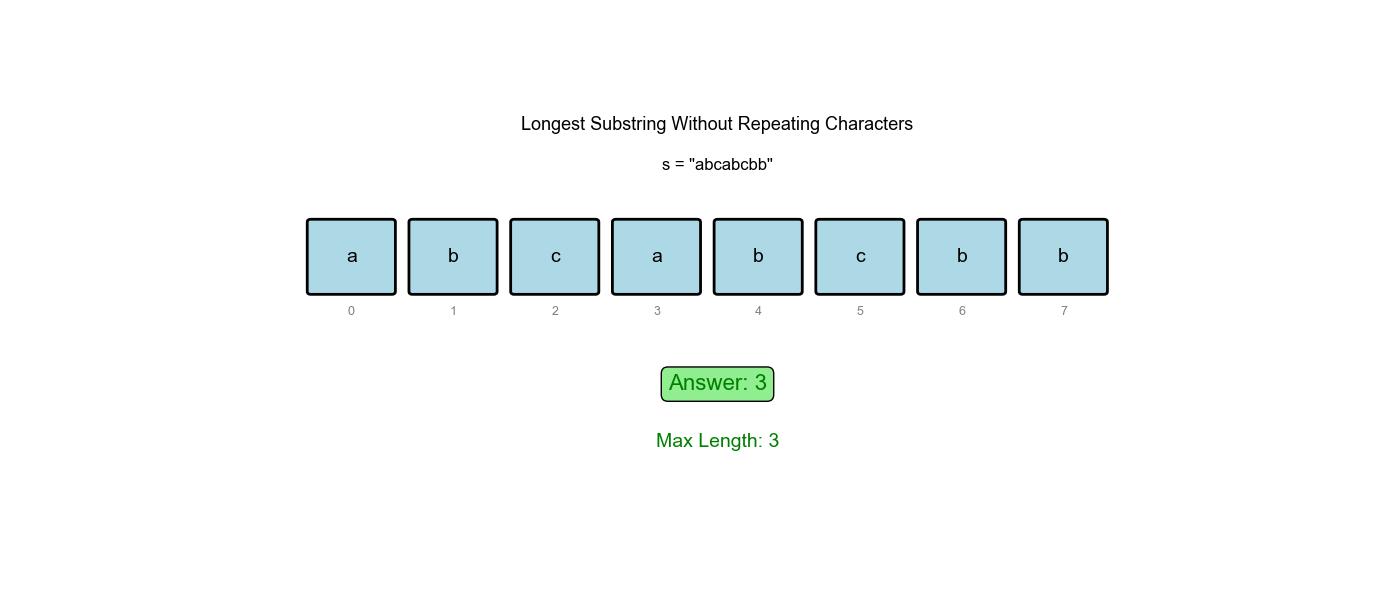
以 s = "abcabcbb" 为例：

1. 初始化：left = 0，right = 0，max_len = 0，char_count = {}

2. right = 0：加入 'a'

   • char_count = {'a': 1}
   • 窗口 [0, 0]："a"，无重复，max_len = 1

3. right = 1：加入 'b'

   • char_count = {'a': 1, 'b': 1}
   • 窗口 [0, 1]："ab"，无重复，max_len = 2

4. right = 2：加入 'c'

   • char_count = {'a': 1, 'b': 1, 'c': 1}
   • 窗口 [0, 2]："abc"，无重复，max_len = 3

5. right = 3：加入 'a'

   • char_count = {'a': 2, 'b': 1, 'c': 1}（出现重复！）
   • 缩小窗口：移动 left，直到 'a' 只出现一次
   • left = 1：移除 s[0] = 'a'，char_count = {'a': 1, 'b': 1, 'c': 1}
   • 窗口 [1, 3]："bca"，无重复，max_len = 3

6. right = 4：加入 'b'

   • char_count = {'a': 1, 'b': 2, 'c': 1}（出现重复！）
   • 缩小窗口：left = 2，移除 s[1] = 'b'
   • 窗口 [2, 4]："cab"，无重复，max_len = 3

7. 继续这个过程...

Python 实现：

def lengthOfLongestSubstring(s):
    """
    找出字符串中无重复字符的最长子串长度
    
    Args:
        s: 输入字符串
    Returns:
        最长无重复字符子串的长度
    
    思路：滑动窗口 + 哈希表
    - 用哈希表记录窗口内每个字符的出现次数
    - 当窗口内出现重复字符（某字符次数 > 1）时，收缩左边界
    - 在窗口满足条件时，更新最大长度
    
    时间复杂度： O(n)，每个字符最多被访问两次
    空间复杂度： O(min(n, m))， m 是字符集大小
    """
    # 边界情况：空字符串
    if not s:
        return 0
  
    left = 0  # 窗口左边界
    max_len = 0  # 记录最长长度
    char_count = {}  # 哈希表：{字符: 出现次数}
  
    # 右指针遍历字符串，扩展窗口
    for right in range(len(s)):
        # 关键步骤 1：将右边界字符加入窗口
        # 为什么用 get？因为字符可能第一次出现，默认为 0
        char_count[s[right]] = char_count.get(s[right], 0) + 1
      
        # 关键步骤 2：收缩窗口（当窗口不满足条件时）
        # 条件： s[right] 的出现次数 > 1，说明窗口内有重复字符
        # 为什么是 while 不是 if？因为可能需要连续移除多个字符
        while char_count[s[right]] > 1:
            # 移除左边界字符
            char_count[s[left]] -= 1
            # 优化：如果字符次数降为 0，从哈希表中删除（节省空间）
            if char_count[s[left]] == 0:
                del char_count[s[left]]
            # 左指针右移
            left += 1
      
        # 关键步骤 3：更新答案（此时窗口满足条件：无重复字符）
        # 窗口大小 = right - left + 1
        max_len = max(max_len, right - left + 1)
  
    return max_len

代码执行过程示例：

输入：s = "abcabcbb"

步骤	right	s[right]	char_count	left	窗口	操作	max_len
初始	-	-	{}	0	""	-	0
1	0	'a'	{'a':1}	0	"a"	加入'a'	1
2	1	'b'	{'a':1,'b':1}	0	"ab"	加入'b'	2
3	2	'c'	{'a':1,'b':1,'c':1}	0	"abc"	加入'c'	3
4	3	'a'	{'a':2,'b':1,'c':1}	0	"abca"	加入'a'，重复！	-
4	3	'a'	{'a':1,'b':1,'c':1}	1	"bca"	移除'a'，不重复	3
5	4	'b'	{'a':1,'b':2,'c':1}	1	"bcab"	加入'b'，重复！	-
5	4	'b'	{'a':1,'b':1,'c':1}	2	"cab"	移除'b'，不重复	3
6	5	'c'	{'a':1,'b':1,'c':2}	2	"cabc"	加入'c'，重复！	-
6	5	'c'	{'a':1,'b':1,'c':1}	3	"abc"	移除'c'，不重复	3
7	6	'b'	{'a':1,'b':2,'c':1}	3	"abcb"	加入'b'，重复！	-
7	6	'b'	{'b':2,'c':1}	4	"bcb"	移除'a'，仍重复	-
7	6	'b'	{'b':1,'c':1}	5	"cb"	移除'b'，不重复	3
8	7	'b'	{'b':2,'c':1}	5	"cbb"	加入'b'，重复！	-
8	7	'b'	{'b':2}	6	"bb"	移除'c'，仍重复	-
8	7	'b'	{'b':1}	7	"b"	移除'b'，不重复	3

为什么这样设计？

1. 一次遍历： right 指针只向右移动，每个字符最多被 right 访问一次
2. 增量更新：每次只处理新加入的字符，不重新检查整个窗口
3. 及时收缩：遇到重复立即收缩左边界，保证窗口始终满足条件
4. 哈希表优化：用哈希表 O(1) 查找字符是否重复，避免遍历窗口

Java 实现：

public int lengthOfLongestSubstring(String s) {
    if (s == null || s.length() == 0) {
        return 0;
    }
  
    int left = 0;
    int maxLen = 0;
    Map<Character, Integer> charCount = new HashMap<>();
  
    for (int right = 0; right < s.length(); right++) {
        char c = s.charAt(right);
        charCount.put(c, charCount.getOrDefault(c, 0) + 1);
      
        // 如果出现重复字符，缩小窗口
        while (charCount.get(c) > 1) {
            char leftChar = s.charAt(left);
            charCount.put(leftChar, charCount.get(leftChar) - 1);
            if (charCount.get(leftChar) == 0) {
                charCount.remove(leftChar);
            }
            left++;
        }
      
        maxLen = Math.max(maxLen, right - left + 1);
    }
  
    return maxLen;
}

复杂度分析

时间复杂度：

推导过程： 1. 外层循环：右指针 right 遍历字符串，执行 次 2. 内层 while 循环：左指针 left 移动，看似嵌套，但关键洞察： - left 只会向右移动，不会回退 - left 最多移动 次（从 0 到 n-1） - 所以内层循环的总执行次数是 ，而不是 3. 哈希表操作：插入/删除/查找都是 $O(1)O(n) + O(n) = O(n)$ 为什么不是 ？

虽然代码中有 for right in range(n) 嵌套 while char_count[s[right]] > 1，但这不是传统的双重循环。关键在于： - 每个字符最多被 left 访问一次，被 right 访问一次 - 所以总操作数是 ，时间复杂度仍是 数值示例： - 字符串长度 100：约 200 次操作（每个字符被访问 2 次） - 字符串长度 1000：约 2000 次操作 - 增长趋势：线性增长，不是 空间复杂度：

推导过程： - 哈希表大小：最多存储窗口内的所有字符 - 最坏情况： - 如果字符串全部不重复：哈希表大小 = （字符串长度） - 但受限于字符集大小 （如 ASCII 是 128， Unicode 常用字符约 65536） - 所以实际大小 = - 最好情况：如果字符串有大量重复，哈希表大小可能远小于 **为什么是 而不是 $ n n m$ - 例如：英文字母字符串，哈希表最多 26 个键，与字符串长度无关

实际例子： - 输入 "abcdefghij...xyz"（ 26 个字母）：哈希表大小 = 26 - 输入 "aaaaaaa..."（ 100 个 'a'）：哈希表大小 = 1 - 输入随机 ASCII 字符串（长度 1000）：哈希表大小 ≤ 128

题目二：最小覆盖子串

LeetCode 76. 最小覆盖子串

给你一个字符串 s、一个字符串 t。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 ""。

示例：

输入: s = "ADOBECODEBANC", t = "ABC"
输出: "BANC"
解释: 最小覆盖子串 "BANC" 包含 'A'、'B' 和 'C'。

思路分析：

这是一个"寻找最短子串"问题。需要：

1. 用哈希表记录 t 中每个字符需要的数量
2. 维护一个窗口，不断扩大窗口直到包含 t 的所有字符
3. 一旦窗口满足条件，尝试缩小窗口，寻找更短的解
4. 记录满足条件的最短窗口

详细步骤：

以 s = "ADOBECODEBANC"，t = "ABC" 为例：

1. 初始化：

   • need = {'A': 1, 'B': 1, 'C': 1}（t 中每个字符需要的数量）
   • window = {}（窗口中每个字符的数量）
   • valid = 0（窗口中满足 need 条件的字符种类数）
   • left = 0，right = 0
   • start = 0，min_len = float('inf')

2. 扩大窗口：

   • right = 0：加入 'A'，window = {'A': 1}，valid = 1（'A' 满足条件）
   • right = 1：加入 'D'，window = {'A': 1, 'D': 1}，valid = 1
   • right = 2：加入 'O'，window = {'A': 1, 'D': 1, 'O': 1}，valid = 1
   • right = 3：加入 'B'，window = {'A': 1, 'B': 1, 'D': 1, 'O': 1}，valid = 2（'B' 满足条件）
   • right = 4：加入 'E'，window = {'A': 1, 'B': 1, 'D': 1, 'E': 1, 'O': 1}，valid = 2
   • right = 5：加入 'C'，window = {'A': 1, 'B': 1, 'C': 1, 'D': 1, 'E': 1, 'O': 1}，valid = 3（所有字符都满足条件！）

3. 缩小窗口（valid == len(need)）：

   • 当前窗口 [0, 5]："ADOBEC"，长度为 6
   • 尝试缩小：left = 0，移除 'A'，但 'A' 是必需的，不能移除
   • 实际上，需要检查移除字符后是否还满足条件
   • 正确的做法：当 window[s[left]] > need.get(s[left], 0) 时，可以移除

4. 继续扩大窗口：

   • right = 6：加入 'O'...
   • 当窗口再次满足条件时，尝试缩小并更新答案

Python 实现：

def minWindow(s, t):
    if not s or not t:
        return ""
  
    # 记录 t 中每个字符需要的数量
    need = {}
    for c in t:
        need[c] = need.get(c, 0) + 1
  
    # 记录窗口中每个字符的数量
    window = {}
    left = 0
    valid = 0  # 窗口中满足 need 条件的字符种类数
    start = 0
    min_len = float('inf')
  
    for right in range(len(s)):
        c = s[right]
        # 扩大窗口
        if c in need:
            window[c] = window.get(c, 0) + 1
            if window[c] == need[c]:
                valid += 1
      
        # 判断窗口是否需要收缩
        while valid == len(need):
            # 更新最小覆盖子串
            if right - left + 1 < min_len:
                start = left
                min_len = right - left + 1
          
            # 缩小窗口
            d = s[left]
            left += 1
            if d in need:
                if window[d] == need[d]:
                    valid -= 1
                window[d] -= 1
  
    return "" if min_len == float('inf') else s[start:start + min_len]

Java 实现：

public String minWindow(String s, String t) {
    if (s == null || t == null || s.length() == 0 || t.length() == 0) {
        return "";
    }
  
    // 记录 t 中每个字符需要的数量
    Map<Character, Integer> need = new HashMap<>();
    for (char c : t.toCharArray()) {
        need.put(c, need.getOrDefault(c, 0) + 1);
    }
  
    // 记录窗口中每个字符的数量
    Map<Character, Integer> window = new HashMap<>();
    int left = 0;
    int valid = 0;  // 窗口中满足 need 条件的字符种类数
    int start = 0;
    int minLen = Integer.MAX_VALUE;
  
    for (int right = 0; right < s.length(); right++) {
        char c = s.charAt(right);
        // 扩大窗口
        if (need.containsKey(c)) {
            window.put(c, window.getOrDefault(c, 0) + 1);
            if (window.get(c).equals(need.get(c))) {
                valid++;
            }
        }
      
        // 判断窗口是否需要收缩
        while (valid == need.size()) {
            // 更新最小覆盖子串
            if (right - left + 1 < minLen) {
                start = left;
                minLen = right - left + 1;
            }
          
            // 缩小窗口
            char d = s.charAt(left);
            left++;
            if (need.containsKey(d)) {
                if (window.get(d).equals(need.get(d))) {
                    valid--;
                }
                window.put(d, window.get(d) - 1);
            }
        }
    }
  
    return minLen == Integer.MAX_VALUE ? "" : s.substring(start, start + minLen);
}

时间复杂度：，其中 和 分别是字符串 s 和 t 的长度 空间复杂度：，用于存储哈希表

题目三：长度最小的子数组

LeetCode 209. 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target，找出该数组中满足其和 ≥ target 的长度最小的连续子数组 [numsl, numsl+1, ..., numsr-1, numsr]，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

输入: target = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的子数组。

思路分析：

这是一个"寻找最短子数组"问题。需要：

1. 维护一个窗口，不断扩大窗口直到窗口和 ≥ target
2. 一旦满足条件，尝试缩小窗口，寻找更短的解
3. 记录满足条件的最短长度

详细步骤：

以 target = 7，nums = [2,3,1,2,4,3] 为例：

1. 初始化：left = 0，right = 0，window_sum = 0，min_len = float('inf')

2. 扩大窗口：

   • right = 0：加入 2，window_sum = 2，窗口 [0, 0]：[2]，和 < 7
   • right = 1：加入 3，window_sum = 5，窗口 [0, 1]：[2,3]，和 < 7
   • right = 2：加入 1，window_sum = 6，窗口 [0, 2]：[2,3,1]，和 < 7
   • right = 3：加入 2，window_sum = 8，窗口 [0, 3]：[2,3,1,2]，和 ≥ 7！

3. 缩小窗口：

   • 当前窗口 [0, 3] 长度为 4，min_len = 4
   • left = 0：移除 2，window_sum = 6，窗口 [1, 3]：[3,1,2]，和 < 7，停止缩小
   • 继续扩大窗口...

4. 继续过程：

   • right = 4：加入 4，window_sum = 10，窗口 [1, 4]：[3,1,2,4]，和 ≥ 7
   • 缩小：left = 1，移除 3，window_sum = 7，窗口 [2, 4]：[1,2,4]，和 ≥ 7
   • 缩小：left = 2，移除 1，window_sum = 6，和 < 7，停止
   • min_len = min(4, 3) = 3

5. 最终：right = 5，加入 3，window_sum = 9，窗口 [2, 5]：[2,4,3]，和 ≥ 7

   • 缩小：left = 2，移除 2，window_sum = 7，窗口 [3, 5]：[4,3]，和 ≥ 7
   • 缩小：left = 3，移除 4，window_sum = 3，和 < 7，停止
   • min_len = min(3, 2) = 2

Python 实现：

def minSubArrayLen(target, nums):
    if not nums:
        return 0
  
    left = 0
    window_sum = 0
    min_len = float('inf')
  
    for right in range(len(nums)):
        # 扩大窗口
        window_sum += nums[right]
      
        # 当窗口和满足条件时，尝试缩小窗口
        while window_sum >= target:
            min_len = min(min_len, right - left + 1)
            window_sum -= nums[left]
            left += 1
  
    return 0 if min_len == float('inf') else min_len

Java 实现：

public int minSubArrayLen(int target, int[] nums) {
    if (nums == null || nums.length == 0) {
        return 0;
    }
  
    int left = 0;
    int windowSum = 0;
    int minLen = Integer.MAX_VALUE;
  
    for (int right = 0; right < nums.length; right++) {
        // 扩大窗口
        windowSum += nums[right];
      
        // 当窗口和满足条件时，尝试缩小窗口
        while (windowSum >= target) {
            minLen = Math.min(minLen, right - left + 1);
            windowSum -= nums[left];
            left++;
        }
    }
  
    return minLen == Integer.MAX_VALUE ? 0 : minLen;
}

时间复杂度：，每个元素最多被访问两次 空间复杂度：

题目四：字符串的排列

LeetCode 567. 字符串的排列

给你两个字符串 s1 和 s2，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true；否则，返回 false。

换句话说，s1 的排列之一是 s2 的子串。

示例：

输入: s1 = "ab" s2 = "eidbaooo"
输出: true
解释: s2 包含 s1 的排列之一 ("ba").

思路分析：

这个问题可以转化为：在 s2 中是否存在一个长度为 len(s1) 的子串，其字符频率与 s1 完全相同。

可以：

1. 用固定大小的窗口（大小为 len(s1)）在 s2 上滑动
2. 对于每个窗口，检查窗口内字符的频率是否与 s1 相同
3. 如果相同，返回 true

Python 实现：

def checkInclusion(s1, s2):
    if len(s1) > len(s2):
        return False
  
    # 记录 s1 中每个字符需要的数量
    need = {}
    for c in s1:
        need[c] = need.get(c, 0) + 1
  
    # 记录窗口中每个字符的数量
    window = {}
    left = 0
  
    # 初始化窗口 [0, len(s1)-1]
    for right in range(len(s1)):
        c = s2[right]
        window[c] = window.get(c, 0) + 1
  
    # 检查第一个窗口
    if window == need:
        return True
  
    # 滑动窗口
    for right in range(len(s1), len(s2)):
        # 加入右边界字符
        c = s2[right]
        window[c] = window.get(c, 0) + 1
      
        # 移除左边界字符
        d = s2[left]
        window[d] -= 1
        if window[d] == 0:
            del window[d]
        left += 1
      
        # 检查窗口
        if window == need:
            return True
  
    return False

优化版本（使用 valid 计数，避免每次比较整个字典）：

def checkInclusion(s1, s2):
    if len(s1) > len(s2):
        return False
  
    need = {}
    for c in s1:
        need[c] = need.get(c, 0) + 1
  
    window = {}
    left = 0
    valid = 0
  
    for right in range(len(s2)):
        c = s2[right]
        # 扩大窗口
        if c in need:
            window[c] = window.get(c, 0) + 1
            if window[c] == need[c]:
                valid += 1
      
        # 如果窗口大小超过 len(s1)，缩小窗口
        if right - left + 1 > len(s1):
            d = s2[left]
            left += 1
            if d in need:
                if window[d] == need[d]:
                    valid -= 1
                window[d] -= 1
      
        # 检查是否满足条件
        if valid == len(need):
            return True
  
    return False

Java 实现：

public boolean checkInclusion(String s1, String s2) {
    if (s1.length() > s2.length()) {
        return false;
    }
  
    Map<Character, Integer> need = new HashMap<>();
    for (char c : s1.toCharArray()) {
        need.put(c, need.getOrDefault(c, 0) + 1);
    }
  
    Map<Character, Integer> window = new HashMap<>();
    int left = 0;
    int valid = 0;
  
    for (int right = 0; right < s2.length(); right++) {
        char c = s2.charAt(right);
        // 扩大窗口
        if (need.containsKey(c)) {
            window.put(c, window.getOrDefault(c, 0) + 1);
            if (window.get(c).equals(need.get(c))) {
                valid++;
            }
        }
      
        // 如果窗口大小超过 len(s1)，缩小窗口
        if (right - left + 1 > s1.length()) {
            char d = s2.charAt(left);
            left++;
            if (need.containsKey(d)) {
                if (window.get(d).equals(need.get(d))) {
                    valid--;
                }
                window.put(d, window.get(d) - 1);
            }
        }
      
        // 检查是否满足条件
        if (valid == need.size()) {
            return true;
        }
    }
  
    return false;
}

时间复杂度：空间复杂度：

题目五：找到字符串中所有字母异位词

LeetCode 438. 找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的字母异位词的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

字母异位词指字母相同，但排列不同的字符串。

示例：

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的字母异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的字母异位词。

思路分析：

这个问题与上一题非常相似，区别在于：

• 上一题只需要判断是否存在，这一题需要找到所有满足条件的起始索引
• 窗口大小固定为 len(p)
• 对于每个满足条件的窗口，记录其起始索引

Python 实现：

def findAnagrams(s, p):
    if len(p) > len(s):
        return []
  
    need = {}
    for c in p:
        need[c] = need.get(c, 0) + 1
  
    window = {}
    left = 0
    valid = 0
    result = []
  
    for right in range(len(s)):
        c = s[right]
        # 扩大窗口
        if c in need:
            window[c] = window.get(c, 0) + 1
            if window[c] == need[c]:
                valid += 1
      
        # 如果窗口大小超过 len(p)，缩小窗口
        if right - left + 1 > len(p):
            d = s[left]
            left += 1
            if d in need:
                if window[d] == need[d]:
                    valid -= 1
                window[d] -= 1
      
        # 检查是否满足条件
        if valid == len(need) and right - left + 1 == len(p):
            result.append(left)
  
    return result

Java 实现：

public List<Integer> findAnagrams(String s, String p) {
    List<Integer> result = new ArrayList<>();
    if (p.length() > s.length()) {
        return result;
    }
  
    Map<Character, Integer> need = new HashMap<>();
    for (char c : p.toCharArray()) {
        need.put(c, need.getOrDefault(c, 0) + 1);
    }
  
    Map<Character, Integer> window = new HashMap<>();
    int left = 0;
    int valid = 0;
  
    for (int right = 0; right < s.length(); right++) {
        char c = s.charAt(right);
        // 扩大窗口
        if (need.containsKey(c)) {
            window.put(c, window.getOrDefault(c, 0) + 1);
            if (window.get(c).equals(need.get(c))) {
                valid++;
            }
        }
      
        // 如果窗口大小超过 len(p)，缩小窗口
        if (right - left + 1 > p.length()) {
            char d = s.charAt(left);
            left++;
            if (need.containsKey(d)) {
                if (window.get(d).equals(need.get(d))) {
                    valid--;
                }
                window.put(d, window.get(d) - 1);
            }
        }
      
        // 检查是否满足条件
        if (valid == need.size() && right - left + 1 == p.length()) {
            result.add(left);
        }
    }
  
    return result;
}

时间复杂度：空间复杂度：

时间复杂度分析

滑动窗口算法的时间复杂度分析有一个通用的方法：

基本分析

对于滑动窗口算法：

• 外层循环：right 指针从 0 移动到 n-1，共 次迭代
• 内层循环：left 指针的移动

虽然有一个 while 循环，但 left 指针只会向前移动，不会后退。因此，在整个算法执行过程中：

• right 指针移动了 次
• left 指针最多移动 次

所以总的时间复杂度是 ，而不是 。

摊还分析（ Amortized Analysis）

可以用摊还分析来更严格地证明：

设 right 移动了 次，left 移动了 次。由于 left 不会超过 right，所以 。

总操作数 = right 移动次数 + left 移动次数 = 因此，每个元素的摊还时间复杂度是 ，总时间复杂度是 。

不同情况的时间复杂度

1. 固定窗口大小：

   • 每个元素被访问两次（一次加入，一次移出）

2. 可变窗口大小（最长子串）：

   • 每个元素最多被访问两次

3. 可变窗口大小（最短子串）：

   • 每个元素最多被访问两次

4. 需要排序或复杂操作：可能更高

   • 例如，如果窗口内需要维护有序结构，可能是

常见陷阱与调试技巧

陷阱一：窗口边界处理错误

问题：窗口的左右边界 [left, right] 是闭区间还是左闭右开区间？

解决方案：

• 统一使用左闭右闭区间 [left, right]
• 窗口长度 = right - left + 1
• 初始化时，left = 0，right = -1（空窗口）或 left = 0，right = 0（包含第一个元素）

示例：

# 错误：窗口长度计算错误
window_len = right - left  # 应该是 right - left + 1

# 正确
window_len = right - left + 1

陷阱二：哈希表更新时机错误

问题：在缩小窗口时，忘记更新哈希表，或者在更新哈希表之前就检查条件。

解决方案：

• 先更新窗口状态（加入/移除元素）
• 再检查窗口是否满足条件
• 最后更新答案

示例：

# 错误：先检查条件，再更新窗口
if window_satisfies_condition():
    update_answer()
    window.remove(s[left])  # 错误：应该在检查之前更新

# 正确：先更新窗口，再检查条件
window.add(s[right])
if window_satisfies_condition():
    update_answer()
window.remove(s[left])

陷阱三： valid 计数更新错误

问题：在使用 valid 计数优化时，更新 valid 的时机不对。

解决方案：

• 当 window[c] == need[c] 时，valid++
• 当 window[c] 从 need[c] 变为 need[c] - 1 时，valid--
• 注意：只有当 window[c] 恰好等于 need[c] 时，才计入 valid

示例：

# 错误：没有检查是否恰好相等
if window[c] >= need[c]:  # 错误：可能重复计数
    valid += 1

# 正确：检查是否恰好相等
if window[c] == need[c]:
    valid += 1

陷阱四：空窗口或边界条件

问题：没有处理空字符串、空数组、窗口大小为 0 等边界情况。

解决方案：

• 在函数开始处检查边界条件
• 确保窗口大小至少为 1（如果需要）

示例：

def sliding_window(s):
    if not s:  # 处理空字符串
        return 0
  
    if len(s) < k:  # 处理窗口大小大于字符串长度的情况
        return []
  
    # ... 主逻辑

调试技巧

1. 打印窗口状态：

def sliding_window(s):
    left = 0
    for right in range(len(s)):
        # 打印当前窗口
        print(f"窗口 [{left}, {right}]: {s[left:right+1]}")
        print(f"窗口状态: {window}")
        # ... 其他逻辑

2. 使用断言检查不变量：

# 检查窗口大小
assert right - left + 1 >= 0, "窗口大小不能为负"

# 检查 valid 计数
assert valid <= len(need), "valid 不能超过 need 的大小"

3. 单步调试：

   • 使用调试器逐步执行
   • 观察 left、right、window、valid 的变化
   • 检查每个步骤是否符合预期

4. 测试用例：

   • 空输入
   • 单个元素
   • 所有元素相同
   • 无解的情况
   • 多个解的情况

❓ Q&A: 滑动窗口常见问题

Q1: 什么时候应该使用滑动窗口？

A: 当你遇到以下关键词时，可以考虑滑动窗口：

• 连续子数组/子串：问题要求找到连续的区间
• 最长/最短：需要找到满足条件的最长或最短区间
• 固定大小：窗口大小固定（如长度为 k 的子数组）
• 包含/不包含：窗口需要包含或不包含某些元素

典型场景：

• 字符串匹配、子串查找
• 数组中的连续子数组问题
• 需要维护窗口内某些统计信息的问题

Q2: 滑动窗口和双指针有什么区别？

A: 滑动窗口是双指针技巧的一种特殊应用：

• 双指针：两个指针可以以任意方式移动（同向、反向、快慢指针等）
• 滑动窗口：两个指针（ left 和 right）维护一个连续的区间，通常 right 先移动， left 后移动

滑动窗口可以看作是一种约束更严格的双指针，专门用于解决连续区间问题。

Q3: 如何判断窗口应该扩大还是缩小？

A: 这取决于问题的目标：

寻找最长子串/子数组：

• 先扩大窗口（移动 right），直到窗口不满足条件
• 然后缩小窗口（移动 left），直到窗口再次满足条件
• 在窗口满足条件时更新答案

寻找最短子串/子数组：

• 先扩大窗口（移动 right），直到窗口满足条件
• 然后缩小窗口（移动 left），尝试找到更短的解
• 在窗口满足条件时更新答案

固定窗口大小：

• 同时移动 left 和 right，保持窗口大小不变

Q4: 为什么滑动窗口的时间复杂度是 O(n) 而不是 O(n ²)？

A: left 指针只会向前移动，不会后退。

虽然有一个 while 循环，但：

• right 指针移动了 次
• left 指针最多移动 次（因为 left <= right）

总操作数 = 每个元素最多被访问两次（一次加入窗口，一次移出窗口），所以时间复杂度是 。

Q5: 如何处理窗口内有重复元素的情况？

A: 这取决于问题的要求：

不允许重复（如"无重复字符的最长子串"）：

• 使用哈希表记录每个元素的出现次数
• 当某个元素出现次数 > 1 时，缩小窗口直到该元素只出现一次

允许重复但有限制（如"最多包含 k 个重复元素"）：

• 使用哈希表记录每个元素的出现次数
• 当某个元素出现次数 > k 时，缩小窗口

完全允许重复：

• 不需要特殊处理，按正常逻辑即可

Q6: valid 计数是什么？为什么要用它？

A: valid 计数用于优化窗口条件的检查。

不使用 valid：

# 每次都要比较整个字典，时间复杂度 O(m)，其中 m 是字符集大小
if window == need:
    # 满足条件

使用 valid：

# 只需要检查 valid == len(need)，时间复杂度 O(1)
if valid == len(need):
    # 满足条件

valid 表示窗口中恰好满足 need 条件的字符种类数。当 valid == len(need) 时，说明窗口中所有需要的字符都满足条件了。

Q7: 滑动窗口可以解决哪些 LeetCode 题目？

A: 以下是一些经典的滑动窗口题目：

固定窗口大小：

• 643. 子数组最大平均值
• 1343. 大小为 K 且平均值大于等于阈值的子数组数目
• 239. 滑动窗口最大值（需要特殊数据结构）

可变窗口大小（最长）：

• 3. 无重复字符的最长子串
• 159. 至多包含两个不同字符的最长子串
• 340. 至多包含 K 个不同字符的最长子串

可变窗口大小（最短）：

• 76. 最小覆盖子串
• 209. 长度最小的子数组
• 713. 乘积小于 K 的子数组

其他：

• 567. 字符串的排列
• 438. 找到字符串中所有字母异位词
• 30. 串联所有单词的子串

Q8: 滑动窗口在字符串和数组问题中有什么区别？

A: 本质上没有区别，都是维护一个连续的区间。主要区别在于：

字符串问题：

• 通常需要处理字符频率、字符匹配等
• 可能需要使用哈希表记录字符出现次数
• 窗口大小可能固定（如找固定长度的子串）或可变

数组问题：

• 通常需要处理数值和、最大值、最小值等
• 可能需要维护窗口内的统计信息（和、积等）
• 窗口大小可能固定或可变

核心思路是一样的：维护窗口状态，通过移动边界来遍历所有可能的子区间。

Q9: 如何优化滑动窗口的空间复杂度？

A: 几种优化方法：

1. 使用数组代替哈希表（如果字符集/数值范围较小）：

# 如果字符都是小写字母，可以用数组代替哈希表
count = [0] * 26
count[ord(c) - ord('a')] += 1

2. 原地更新（如果不需要保留原数组）：

# 直接在原数组上操作，不创建新数组

3. 只记录必要信息：

# 只记录窗口内需要的信息，而不是所有信息
# 例如，只需要记录字符频率，不需要记录字符位置

4. 使用 valid 计数：

# 避免每次比较整个字典，减少空间和时间开销

Q10: 滑动窗口算法有哪些常见的变体？

A: 常见的变体包括：

1. 多指针滑动窗口：

   • 使用三个或更多指针维护多个窗口
   • 例如：同时维护多个不同大小的窗口

2. 滑动窗口 + 数据结构：

   • 窗口内需要维护有序结构（如堆、平衡树）
   • 例如： 239. 滑动窗口最大值（需要维护窗口内的最大值）

3. 滑动窗口 + 前缀和：

   • 结合前缀和优化窗口和的计算
   • 例如： 560. 和为 K 的子数组

4. 滑动窗口 + 动态规划：

   • 窗口状态需要动态规划来维护
   • 例如：一些复杂的字符串匹配问题

5. 滑动窗口 + 二分查找：

   • 窗口大小不确定，需要二分查找最优大小
   • 例如：某些优化问题

变体与扩展问题

变体一：多窗口问题

有些问题需要同时维护多个窗口，或者在不同条件下使用不同的窗口策略。

例题：至多包含两个不同字符的最长子串（ LeetCode 159）

def lengthOfLongestSubstringTwoDistinct(s):
    if len(s) <= 2:
        return len(s)
  
    left = 0
    char_count = {}
    max_len = 0
  
    for right in range(len(s)):
        char_count[s[right]] = char_count.get(s[right], 0) + 1
      
        # 当字符种类超过 2 时，缩小窗口
        while len(char_count) > 2:
            char_count[s[left]] -= 1
            if char_count[s[left]] == 0:
                del char_count[s[left]]
            left += 1
      
        max_len = max(max_len, right - left + 1)
  
    return max_len

关键点：使用 len(char_count) 来判断窗口内字符种类数，而不是用 valid 计数。

变体二：滑动窗口 + 前缀和

当需要快速计算窗口和时，可以结合前缀和优化。

例题：和为 K 的子数组（ LeetCode 560）

虽然这道题通常用哈希表解决，但也可以用滑动窗口的思想理解：维护一个窗口，当窗口和等于 K 时计数。

def subarraySum(nums, k):
    count = 0
    prefix_sum = 0
    sum_map = {0: 1}  # 前缀和为 0 出现 1 次
  
    for num in nums:
        prefix_sum += num
        # 如果存在前缀和 prefix_sum - k，说明存在子数组和为 k
        if prefix_sum - k in sum_map:
            count += sum_map[prefix_sum - k]
        sum_map[prefix_sum] = sum_map.get(prefix_sum, 0) + 1
  
    return count

变体三：滑动窗口 + 双指针

有些问题需要结合双指针技巧，在窗口内进行更复杂的操作。

例题：最小区间（ LeetCode 632）

需要在多个有序数组中找到包含每个数组至少一个元素的最小区间。可以用滑动窗口的思想，配合双指针在多个数组间移动。

扩展问题推荐

1. 困难级别：

   • 30. 串联所有单词的子串：固定窗口大小，但需要处理单词匹配
   • 76. 最小覆盖子串：可变窗口，需要维护字符频率
   • 239. 滑动窗口最大值：固定窗口，需要维护最大值（用单调队列）

2. 中等难度：

   • 159. 至多包含两个不同字符的最长子串
   • 340. 至多包含 K 个不同字符的最长子串
   • 424. 替换后的最长重复字符
   • 713. 乘积小于 K 的子数组

3. 简单级别：

   • 643. 子数组最大平均值
   • 1343. 大小为 K 且平均值大于等于阈值的子数组数目

实战建议

如何快速识别滑动窗口问题

看到以下关键词时，优先考虑滑动窗口：

• 连续子数组/子串：问题明确要求连续区间
• 最长/最短：需要找到满足条件的最长或最短区间
• 固定长度：窗口大小固定（如长度为 k）
• 包含/不包含：窗口需要包含或不包含某些元素
• 和/积/频率：需要维护窗口内的统计信息

解题步骤

1. 确定窗口类型：

   • 固定大小：窗口大小不变，同时移动左右边界
   • 可变大小：先扩大窗口，满足条件后缩小

2. 确定窗口状态：

   • 需要记录什么信息？（字符频率、和、最大值等）
   • 用什么数据结构？（哈希表、数组、变量）

3. 确定收缩条件：

   • 什么时候缩小窗口？
   • 缩小到什么时候停止？

4. 更新答案的时机：

   • 在扩大窗口时更新？
   • 在缩小窗口时更新？
   • 在满足条件时更新？

常见陷阱与避免方法

陷阱一：窗口边界处理

# 错误：窗口长度计算错误
window_len = right - left  # 应该是 right - left + 1

# 正确
window_len = right - left + 1

陷阱二：哈希表更新顺序

# 错误：先检查条件，再更新窗口
if window_satisfies_condition():
    update_answer()
    window.remove(s[left])  # 应该在检查前更新

# 正确：先更新窗口，再检查条件
window.add(s[right])
if window_satisfies_condition():
    update_answer()
window.remove(s[left])

陷阱三： valid 计数错误

# 错误：没有检查是否恰好相等
if window[c] >= need[c]:  # 可能重复计数
    valid += 1

# 正确：检查是否恰好相等
if window[c] == need[c]:
    valid += 1

调试技巧

1. 打印窗口状态：在关键位置打印 left、right、窗口内容、窗口状态
2. 单步调试：使用调试器逐步执行，观察变量变化
3. 测试边界情况：空输入、单个元素、所有元素相同、无解情况
4. 对比暴力解法：先用暴力法验证思路，再优化为滑动窗口

性能优化建议

1. 空间优化：

   • 如果字符集小（如只有小写字母），用数组代替哈希表
   • 如果只需要计数，不需要具体字符，用变量代替哈希表

2. 时间优化：

   • 使用 valid 计数避免每次比较整个字典
   • 提前终止：如果已经找到最优解，可以提前结束

3. 代码优化：

   • 合并相似逻辑，减少重复代码
   • 使用更高效的数据结构（如 collections.defaultdict）

总结

滑动窗口是一种强大的算法技巧，特别适合解决连续子区间问题。掌握滑动窗口的要点：

1. 理解核心思想：维护一个窗口，通过移动边界遍历所有可能的子区间
2. 识别问题模式：固定窗口大小 vs 可变窗口大小，最长 vs 最短
3. 掌握模板代码：理解扩大窗口、缩小窗口、更新答案的时机
4. 注意边界条件：空输入、窗口大小、边界处理
5. 优化技巧：使用 valid 计数、数组代替哈希表等

通过大量练习，你会发现滑动窗口是解决 LeetCode 中很多问题的"万能钥匙"。记住，算法学习是一个循序渐进的过程，多思考、多练习，你一定能掌握这个技巧！