LeetCode（十）—— 栈与队列
Chen Kai BOSS
  2020-03-10 15:30:00 2020-03-10 15:30      8k 字  32 分钟  

栈和队列是两种最基础的数据结构，也是算法面试中的常客。它们看似简单，但实际应用中却变化多端：从括号匹配到单调栈优化，从 BFS 遍历到优先队列，从滑动窗口到双端队列，几乎每个算法题都可能用到它们。掌握好栈和队列，不仅能解决大量 LeetCode 题目，更能深入理解递归、回溯、 BFS 等算法的本质。

本文将从基础概念出发，通过经典题目深入理解栈和队列的应用场景，然后逐步深入到单调栈、优先队列、双端队列等进阶技巧，最后通过 Q&A 解答常见疑问。每个知识点都配有详细的代码实现和复杂度分析，确保你能真正掌握这些数据结构。

栈与队列的基本概念

栈（ Stack）

栈是一种后进先出（ LIFO, Last In First Out）的线性数据结构。想象一下叠盘子：你只能从最上面取盘子，也只能把新盘子放在最上面。

栈有两个核心操作：

  • push：将元素压入栈顶
  • pop：从栈顶弹出元素

此外还有：

  • peek/top：查看栈顶元素（不删除）
  • isEmpty：判断栈是否为空
  • size：获取栈中元素个数

在 Python 中，可以用列表模拟栈：

1
2
3
4
5
stack = []
stack.append(1)  # push
stack.append(2)
top = stack[-1]  # peek
val = stack.pop()  # pop

队列（ Queue）

队列是一种先进先出（ FIFO, First In First Out）的线性数据结构。就像排队买票：先来的人先买到票，后来的人排在队尾。

队列的核心操作：

  • enqueue/offer：将元素加入队尾
  • dequeue/poll：从队首取出元素
  • peek/front：查看队首元素（不删除）
  • isEmpty：判断队列是否为空
  • size：获取队列中元素个数

在 Python 中，使用 collections.deque 实现队列效率更高：

1
2
3
4
5
6
7
from collections import deque

queue = deque()
queue.append(1)  # enqueue
queue.append(2)
front = queue[0]  # peek
val = queue.popleft()  # dequeue

为什么需要栈和队列？

栈和队列虽然简单，但它们能帮助我们：

  1. 管理递归调用：函数调用栈本质上就是栈
  2. 实现回溯算法： DFS 可以用栈模拟
  3. 层次遍历： BFS 必须用队列
  4. 处理匹配问题：括号、标签匹配等
  5. 优化时间复杂度：单调栈可以 O(n) 解决某些问题

栈的经典应用

有效的括号（ LeetCode 20）

题目：给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

有效字符串需满足：

  • 左括号必须用相同类型的右括号闭合
  • 左括号必须以正确的顺序闭合
  • 注意空字符串可被认为是有效字符串

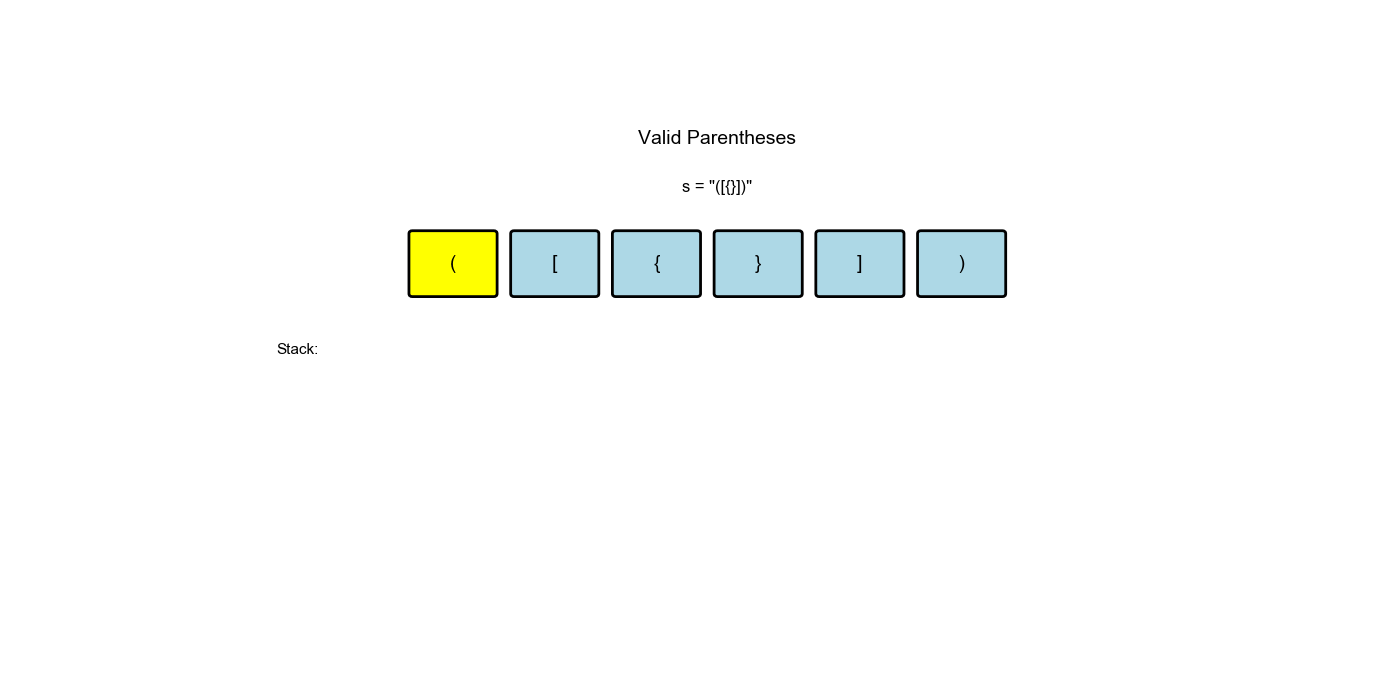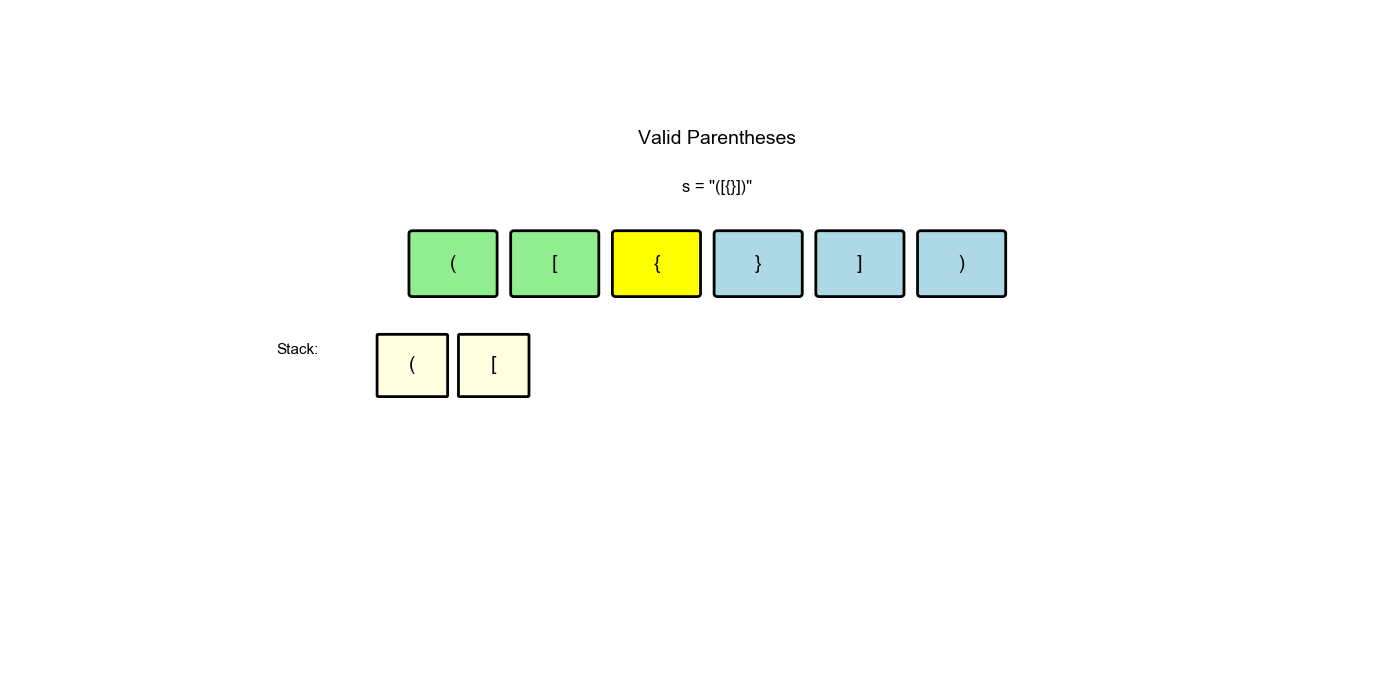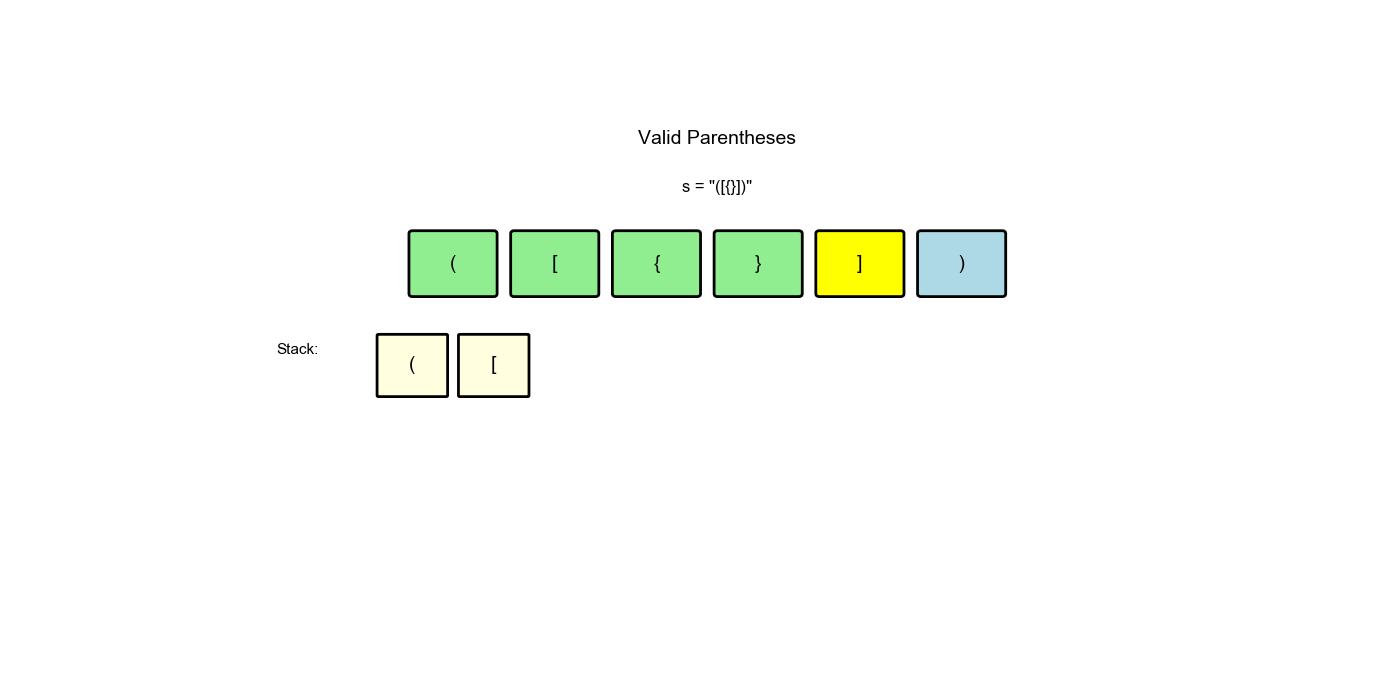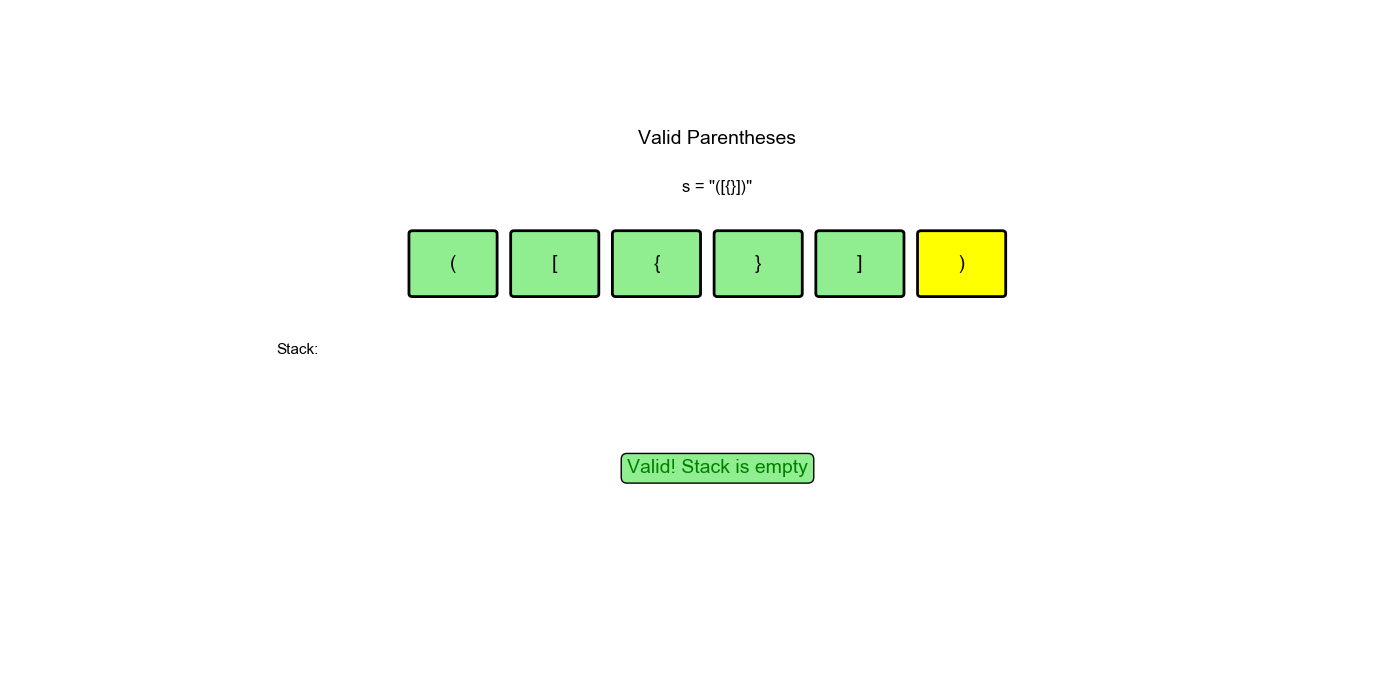
思路：遇到左括号就入栈，遇到右括号就检查栈顶是否匹配。如果匹配就弹出，不匹配或栈为空则无效。

1
2
3
4
5
6
7
8
9
10
11
12
def isValid(s: str) -> bool:
    stack = []
    mapping = {')': '(', '}': '{', ']': '['}
  
    for char in s:
        if char in mapping:  # 右括号
            if not stack or stack.pop() != mapping[char]:
                return False
        else:  # 左括号
            stack.append(char)
  
    return len(stack) == 0

复杂度分析：

  • 时间复杂度：，遍历字符串一次
  • 空间复杂度：，最坏情况下所有字符都是左括号

变式：如果括号可以嵌套多层，或者需要输出最长有效括号子串的长度（ LeetCode 32），思路类似，但需要记录索引。

最小栈（ LeetCode 155）

题目：设计一个支持 push， pop， top 操作，并能在常数时间内检索到最小元素的栈。

思路：如果只用一个栈，获取最小值需要遍历所有元素，时间复杂度是 。可以用两个栈：一个存储所有元素，另一个存储当前最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class MinStack:
    def __init__(self):
        self.stack = []
        self.min_stack = []
  
    def push(self, val: int) -> None:
        self.stack.append(val)
        # 如果 min_stack 为空，或者新值更小，则入栈
        if not self.min_stack or val <= self.min_stack[-1]:
            self.min_stack.append(val)
  
    def pop(self) -> None:
        if self.stack:
            val = self.stack.pop()
            # 如果弹出的是最小值， min_stack 也要弹出
            if self.min_stack and val == self.min_stack[-1]:
                self.min_stack.pop()
  
    def top(self) -> int:
        return self.stack[-1]
  
    def getMin(self) -> int:
        return self.min_stack[-1]

优化：如果允许存储冗余数据，可以简化代码。每次 push 时，如果新值大于当前最小值，仍然把当前最小值再 push 一次到 min_stack：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class MinStack:
    def __init__(self):
        self.stack = []
        self.min_stack = []
  
    def push(self, val: int) -> None:
        self.stack.append(val)
        # 总是 push 当前最小值
        if not self.min_stack:
            self.min_stack.append(val)
        else:
            self.min_stack.append(min(val, self.min_stack[-1]))
  
    def pop(self) -> None:
        self.stack.pop()
        self.min_stack.pop()
  
    def top(self) -> int:
        return self.stack[-1]
  
    def getMin(self) -> int:
        return self.min_stack[-1]

复杂度分析：

  • 所有操作时间复杂度：
  • 空间复杂度：，需要额外的 min_stack

逆波兰表达式求值（ LeetCode 150）

题目：根据逆波兰表示法，求表达式的值。有效的算符包括 +、-、*、/。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

逆波兰表达式（后缀表达式）的特点：

  • 操作符在操作数之后
  • 不需要括号来指定运算顺序
  • 适合用栈来计算

思路：遍历表达式，遇到数字就入栈，遇到运算符就弹出两个数字进行计算，结果再入栈。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def evalRPN(tokens: List[str]) -> int:
    stack = []
  
    for token in tokens:
        if token in ['+', '-', '*', '/']:
            # 注意顺序：先弹出的是右操作数，后弹出的是左操作数
            right = stack.pop()
            left = stack.pop()
          
            if token == '+':
                result = left + right
            elif token == '-':
                result = left - right
            elif token == '*':
                result = left * right
            else:  # '/'
                # 注意：题目要求向零截断，即 truncate toward zero
                result = int(left / right)
          
            stack.append(result)
        else:
            stack.append(int(token))
  
    return stack[0]

注意事项：

  1. 除法运算： Python 的 // 是向下取整，但题目要求向零截断。例如 -7 // 3 = -3，但应该返回 -2。使用 int(left / right) 可以正确处理。
  2. 操作数顺序：减法、除法不满足交换律，要注意左右操作数的顺序。

复杂度分析：

  • 时间复杂度：，遍历一次表达式
  • 空间复杂度：，栈的空间

每日温度（ LeetCode 739）

题目：给定一个整数数组 temperatures，表示每天的温度，返回一个数组 answer，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例：

1
2
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

思路一：暴力法 对于每个位置，向后查找第一个大于它的元素。

1
2
3
4
5
6
7
8
9
10
11
def dailyTemperatures(temperatures: List[int]) -> List[int]:
    n = len(temperatures)
    answer = [0] * n
  
    for i in range(n):
        for j in range(i + 1, n):
            if temperatures[j] > temperatures[i]:
                answer[i] = j - i
                break
  
    return answer

时间复杂度：，空间复杂度：。

思路二：单调栈 维护一个单调递减栈（从栈底到栈顶递减），栈中存储索引。遍历数组：

  • 如果当前温度大于栈顶温度，说明找到了栈顶元素的下一个更高温度，弹出并计算差值
  • 否则将当前索引入栈
1
2
3
4
5
6
7
8
9
10
11
12
13
def dailyTemperatures(temperatures: List[int]) -> List[int]:
    n = len(temperatures)
    answer = [0] * n
    stack = []  # 存储索引
  
    for i in range(n):
        # 当前温度大于栈顶温度
        while stack and temperatures[i] > temperatures[stack[-1]]:
            idx = stack.pop()
            answer[idx] = i - idx
        stack.append(i)
  
    return answer

复杂度分析：

  • 时间复杂度：，每个元素最多入栈和出栈一次
  • 空间复杂度：，栈的空间

为什么单调栈能优化？ 暴力法对每个位置都要向后查找，而单调栈利用了"如果当前元素比栈顶大，那么它可能比栈中其他元素也大"这一性质，避免了重复比较。

单调栈详解

单调栈是栈的一种特殊应用，栈中的元素保持单调性（递增或递减）。它常用于解决"下一个更大/更小元素"、"左边第一个更大/更小元素"等问题。

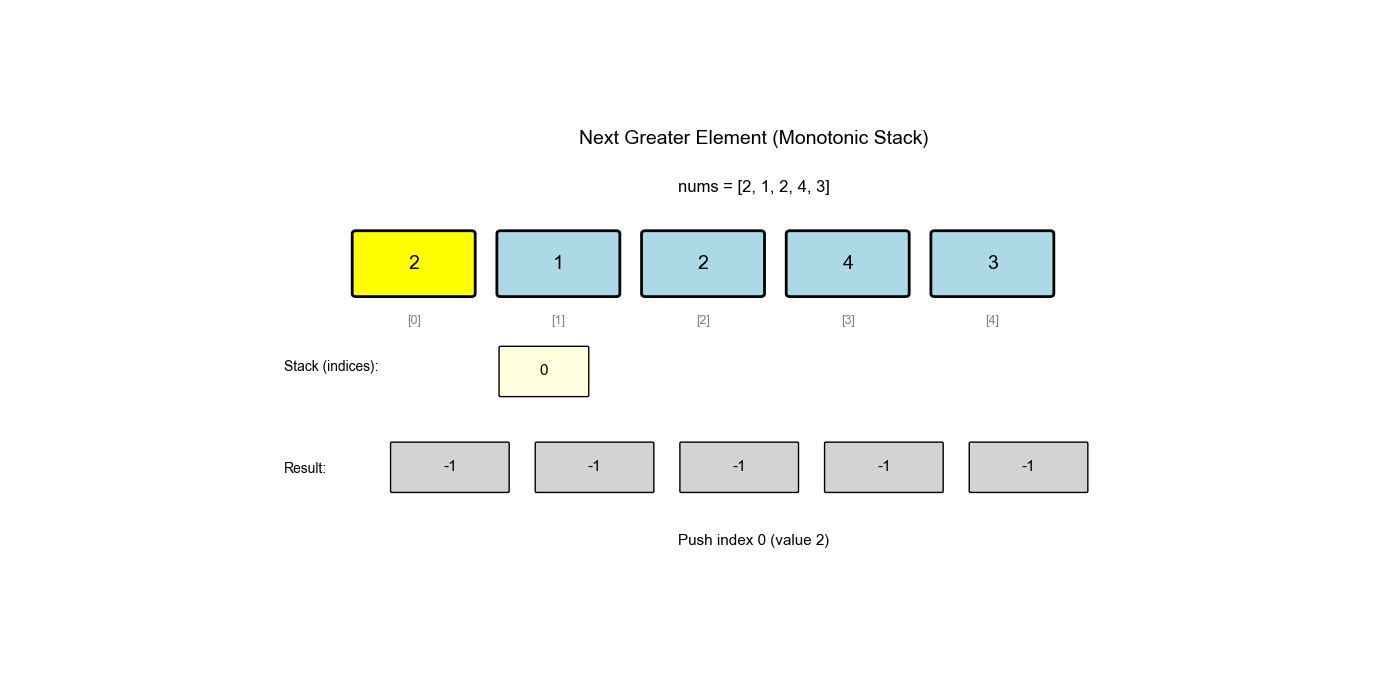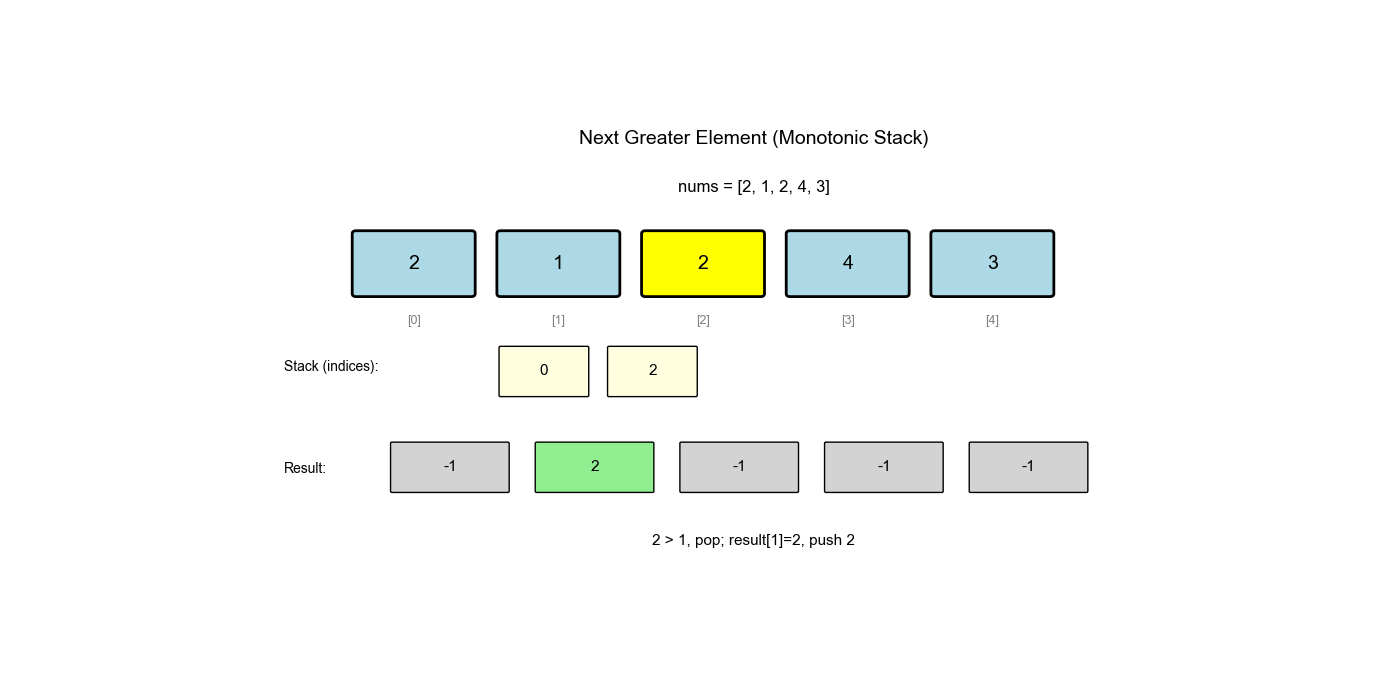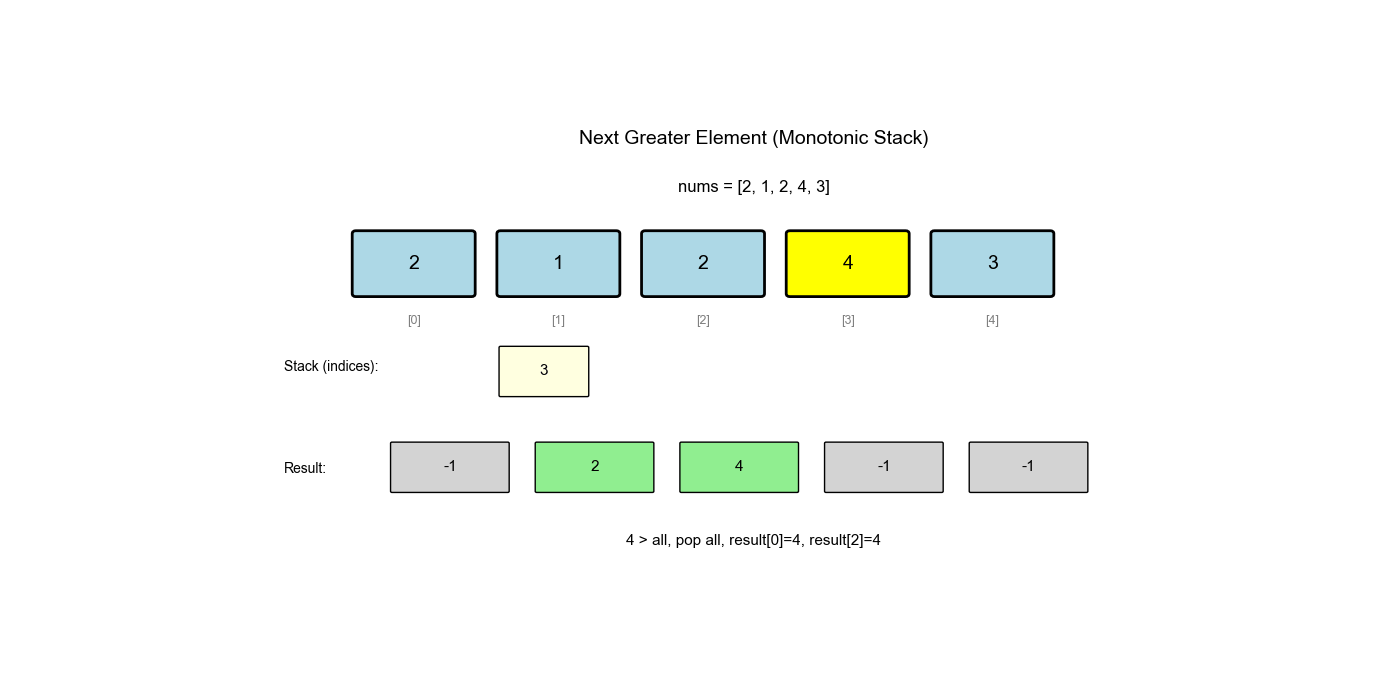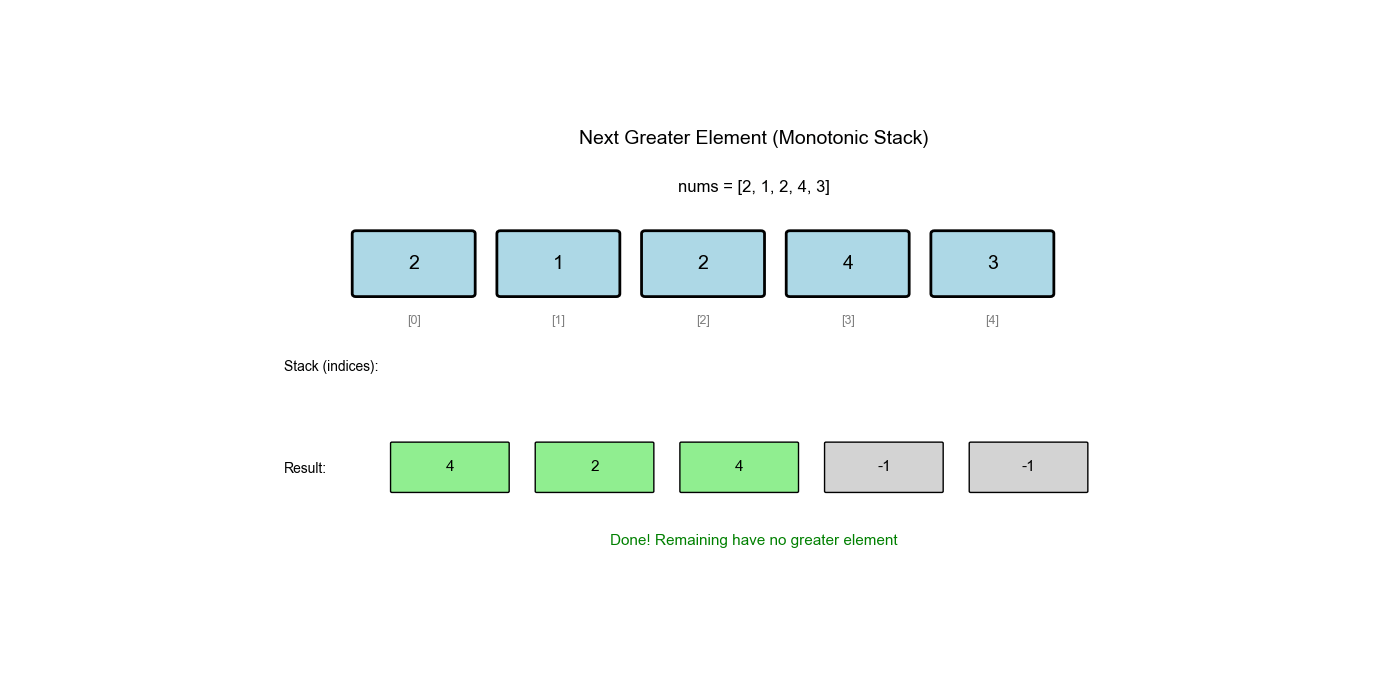
下一个更大元素 I（ LeetCode 496）

题目：nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置右侧的第一个比 x 大的元素。如果不存在，对应位置输出 -1。

思路：先用单调栈找出 nums2 中每个元素的下一个更大元素，存储在哈希表中，然后遍历 nums1 查询。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def nextGreaterElement(nums1: List[int], nums2: List[int]) -> List[int]:
    # 用单调栈找出 nums2 中每个元素的下一个更大元素
    stack = []
    next_greater = {}  # 元素 -> 下一个更大元素
  
    for num in nums2:
        # 当前元素大于栈顶元素
        while stack and num > stack[-1]:
            next_greater[stack.pop()] = num
        stack.append(num)
  
    # 对于栈中剩余元素，它们没有下一个更大元素
    while stack:
        next_greater[stack.pop()] = -1
  
    # 查询 nums1
    return [next_greater.get(num, -1) for num in nums1]

下一个更大元素 II（ LeetCode 503）

题目：给定一个循环数组，输出每个元素的下一个更大元素。如果不存在，则输出 -1。

思路：循环数组可以展开成两倍长度的数组，或者用取模运算模拟循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def nextGreaterElements(nums: List[int]) -> List[int]:
    n = len(nums)
    answer = [-1] * n
    stack = []  # 存储索引
  
    # 遍历两倍长度
    for i in range(2 * n):
        idx = i % n
        while stack and nums[idx] > nums[stack[-1]]:
            answer[stack.pop()] = nums[idx]
        # 只在第一轮遍历时入栈
        if i < n:
            stack.append(idx)
  
    return answer

柱状图中最大的矩形（ LeetCode 84）

题目：给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

思路：对于每个柱子，以它的高度为矩形高度，向左右扩展，找到左右第一个比它矮的柱子，这就是矩形的边界。

使用单调递增栈（从栈底到栈顶递增）：

  • 当当前高度小于栈顶高度时，说明找到了栈顶柱子的右边界
  • 栈中前一个元素就是左边界
  • 计算以栈顶柱子高度为矩形高度的最大面积
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def largestRectangleArea(heights: List[int]) -> int:
    stack = []
    max_area = 0
  
    for i, h in enumerate(heights):
        # 当前高度小于栈顶高度，找到了右边界
        while stack and h < heights[stack[-1]]:
            height = heights[stack.pop()]
            # 左边界：如果栈为空，说明左边没有更矮的，左边界是 -1
            width = i - stack[-1] - 1 if stack else i
            max_area = max(max_area, height * width)
        stack.append(i)
  
    # 处理栈中剩余元素（它们的右边界是数组末尾）
    while stack:
        height = heights[stack.pop()]
        width = len(heights) - stack[-1] - 1 if stack else len(heights)
        max_area = max(max_area, height * width)
  
    return max_area

优化：在数组两端添加高度为 0 的哨兵，简化边界处理：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def largestRectangleArea(heights: List[int]) -> int:
    # 添加哨兵
    heights = [0] + heights + [0]
    stack = [0]  # 先放入左哨兵的索引
    max_area = 0
  
    for i in range(1, len(heights)):
        while heights[i] < heights[stack[-1]]:
            height = heights[stack.pop()]
            width = i - stack[-1] - 1
            max_area = max(max_area, height * width)
        stack.append(i)
  
    return max_area

复杂度分析：

  • 时间复杂度：，每个元素最多入栈和出栈一次
  • 空间复杂度：，栈的空间

接雨水（ LeetCode 42）

题目：给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

思路：使用单调递减栈。当遇到比栈顶高的柱子时，说明形成了一个凹槽，可以接雨水。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def trap(height: List[int]) -> int:
    stack = []
    water = 0
  
    for i, h in enumerate(height):
        while stack and h > height[stack[-1]]:
            bottom = stack.pop()
            if not stack:
                break
            # 左边界、右边界、底边
            left = stack[-1]
            right = i
            # 雨水高度 = min(左边界高度, 右边界高度) - 底边高度
            water_height = min(height[left], height[right]) - height[bottom]
            water_width = right - left - 1
            water += water_height * water_width
        stack.append(i)
  
    return water

复杂度分析：

  • 时间复杂度：
  • 空间复杂度：

队列与 BFS

BFS 的基本思想

广度优先搜索（ BFS）使用队列来实现层次遍历。基本流程：

  1. 将起始节点入队

  2. 当队列不为空时：

    • 取出队首节点
    • 访问该节点
    • 将该节点的所有未访问邻居入队

  3. 重复步骤 2

二叉树的层次遍历（ LeetCode 102）

题目：给你二叉树的根节点 root，返回其节点值的层序遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from collections import deque

def levelOrder(root: TreeNode) -> List[List[int]]:
    if not root:
        return []
  
    result = []
    queue = deque([root])
  
    while queue:
        level_size = len(queue)
        level = []
      
        for _ in range(level_size):
            node = queue.popleft()
            level.append(node.val)
          
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
      
        result.append(level)
  
    return result

关键点：

  • 使用 level_size 记录当前层的节点数，确保每次处理完一层
  • 在遍历当前层时，下一层的节点已经入队

岛屿数量（ LeetCode 200）

题目：给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

思路：遍历网格，遇到 '1' 就用 BFS 标记整个岛屿。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from collections import deque

def numIslands(grid: List[List[str]]) -> int:
    if not grid:
        return 0
  
    m, n = len(grid), len(grid[0])
    directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
    count = 0
  
    def bfs(i, j):
        queue = deque([(i, j)])
        grid[i][j] = '0'  # 标记为已访问
      
        while queue:
            x, y = queue.popleft()
            for dx, dy in directions:
                nx, ny = x + dx, y + dy
                if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] == '1':
                    grid[nx][ny] = '0'
                    queue.append((nx, ny))
  
    for i in range(m):
        for j in range(n):
            if grid[i][j] == '1':
                count += 1
                bfs(i, j)
  
    return count

复杂度分析：

  • 时间复杂度：，每个格子最多访问一次
  • 空间复杂度：，队列的空间，最坏情况下整个网格都是陆地

打开转盘锁（ LeetCode 752）

题目：你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有 10 个数字：'0' 到 '9'。每个拨轮可以自由旋转：例如把 '9' 变为 '0'，'0' 变为 '9'。每次旋转都只能旋转一个拨轮的一个数字。

锁的初始数字为 '0000'，一个代表四个拨轮的数字的字符串。列表 deadends 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，锁将会被永久锁定，无法再被旋转。

给你一个目标数字 target，返回需要的最少旋转次数，如果无论如何不能解锁，返回 -1。

思路： BFS 求最短路径。每个状态有 8 个邻居（ 4 个拨轮，每个可以向上或向下转）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from collections import deque

def openLock(deadends: List[str], target: str) -> int:
    deadends_set = set(deadends)
    if '0000' in deadends_set:
        return -1
  
    queue = deque([('0000', 0)])
    visited = {'0000'}
  
    def get_neighbors(state):
        neighbors = []
        state_list = list(state)
        for i in range(4):
            # 向上转
            temp = state_list[:]
            temp[i] = str((int(temp[i]) + 1) % 10)
            neighbors.append(''.join(temp))
          
            # 向下转
            temp = state_list[:]
            temp[i] = str((int(temp[i]) - 1) % 10)
            neighbors.append(''.join(temp))
      
        return neighbors
  
    while queue:
        state, moves = queue.popleft()
      
        if state == target:
            return moves
      
        for neighbor in get_neighbors(state):
            if neighbor not in visited and neighbor not in deadends_set:
                visited.add(neighbor)
                queue.append((neighbor, moves + 1))
  
    return -1

复杂度分析：

  • 时间复杂度：，最多有 10000 个状态，每个状态有 8 个邻居
  • 空间复杂度：， visited 集合和队列的空间

优先队列（堆）应用

优先队列（ Priority Queue）是一种特殊的队列，每次出队的是优先级最高的元素。在 Python 中，可以使用 heapq 模块实现最小堆。

前 K 个高频元素（ LeetCode 347）

题目：给你一个整数数组 nums 和一个整数 k，请你返回其中出现频率前 k 高的元素。可以按任意顺序返回答案。

思路一：排序 统计频率后排序，时间复杂度 。

思路二：最小堆 维护一个大小为 k 的最小堆，堆顶是频率最小的元素。遍历频率字典，如果堆大小小于 k 或当前频率大于堆顶，则入堆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import heapq
from collections import Counter

def topKFrequent(nums: List[int], k: int) -> List[int]:
    # 统计频率
    counter = Counter(nums)
  
    # 最小堆
    heap = []
  
    for num, freq in counter.items():
        if len(heap) < k:
            heapq.heappush(heap, (freq, num))
        elif freq > heap[0][0]:
            heapq.heapreplace(heap, (freq, num))
  
    return [num for freq, num in heap]

思路三：桶排序 如果频率范围已知，可以用桶排序，时间复杂度 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from collections import Counter

def topKFrequent(nums: List[int], k: int) -> List[int]:
    counter = Counter(nums)
    # 桶：索引是频率，值是数字列表
    buckets = [[] for _ in range(len(nums) + 1)]
  
    for num, freq in counter.items():
        buckets[freq].append(num)
  
    result = []
    # 从高频到低频遍历
    for i in range(len(nums), 0, -1):
        result.extend(buckets[i])
        if len(result) >= k:
            break
  
    return result[:k]

复杂度分析：

  • 堆方法：时间复杂度 ，空间复杂度
  • 桶排序：时间复杂度 ，空间复杂度

合并 K 个升序链表（ LeetCode 23）

题目：给你一个链表数组，每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中，返回合并后的链表。

思路：使用最小堆，每次取出最小的节点，然后将其下一个节点入堆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import heapq

def mergeKLists(lists: List[ListNode]) -> ListNode:
    # 最小堆：存储 (值, 节点索引, 节点)
    heap = []
  
    # 初始化：每个链表的头节点入堆
    for i, node in enumerate(lists):
        if node:
            heapq.heappush(heap, (node.val, i, node))
  
    dummy = ListNode(0)
    current = dummy
  
    while heap:
        val, idx, node = heapq.heappop(heap)
        current.next = node
        current = current.next
      
        # 如果该链表还有下一个节点，入堆
        if node.next:
            heapq.heappush(heap, (node.next.val, idx, node.next))
  
    return dummy.next

复杂度分析：

  • 时间复杂度：，其中 是所有节点数， 是链表数
  • 空间复杂度：，堆的大小

数据流的中位数（ LeetCode 295）

题目：中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

设计一个支持以下两种操作的数据结构：

  • void addNum(int num)：从数据流中添加一个整数到数据结构中
  • double findMedian()：返回目前所有元素的中位数

思路：使用两个堆：一个大顶堆存储较小的一半，一个小顶堆存储较大的一半。保持两个堆的大小差不超过 1 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import heapq

class MedianFinder:
    def __init__(self):
        # 大顶堆：存储较小的一半（ Python 的 heapq 是最小堆，所以用负数）
        self.max_heap = []
        # 小顶堆：存储较大的一半
        self.min_heap = []
  
    def addNum(self, num: int) -> None:
        # 先加入大顶堆
        heapq.heappush(self.max_heap, -num)
      
        # 保证大顶堆的最大值 <= 小顶堆的最小值
        if self.max_heap and self.min_heap and -self.max_heap[0] > self.min_heap[0]:
            val = -heapq.heappop(self.max_heap)
            heapq.heappush(self.min_heap, val)
      
        # 平衡两个堆的大小
        if len(self.max_heap) > len(self.min_heap) + 1:
            val = -heapq.heappop(self.max_heap)
            heapq.heappush(self.min_heap, val)
        elif len(self.min_heap) > len(self.max_heap) + 1:
            val = heapq.heappop(self.min_heap)
            heapq.heappush(self.max_heap, -val)
  
    def findMedian(self) -> float:
        if len(self.max_heap) > len(self.min_heap):
            return -self.max_heap[0]
        elif len(self.min_heap) > len(self.max_heap):
            return self.min_heap[0]
        else:
            return (-self.max_heap[0] + self.min_heap[0]) / 2.0

复杂度分析：

  • addNum：
  • findMedian：
  • 空间复杂度：

双端队列（滑动窗口最大值）

双端队列（ Deque）允许在两端进行插入和删除操作。在 Python 中，collections.deque 提供了高效的双端队列实现。

滑动窗口最大值（ LeetCode 239）

题目：给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。

思路一：暴力法 对每个窗口，遍历找到最大值。时间复杂度 。

思路二：单调队列 维护一个单调递减的双端队列，队首是当前窗口的最大值。队列中存储索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from collections import deque

def maxSlidingWindow(nums: List[int], k: int) -> List[int]:
    dq = deque()  # 存储索引
    result = []
  
    for i in range(len(nums)):
        # 移除窗口外的元素
        while dq and dq[0] <= i - k:
            dq.popleft()
      
        # 移除小于当前元素的元素（它们不可能成为最大值）
        while dq and nums[dq[-1]] < nums[i]:
            dq.pop()
      
        dq.append(i)
      
        # 窗口大小达到 k 时，开始记录结果
        if i >= k - 1:
            result.append(nums[dq[0]])
  
    return result

为什么单调队列有效？

  • 如果新元素大于队列中的某些元素，那么这些元素在后续窗口中也不可能成为最大值（因为新元素更大且更靠后）
  • 因此可以安全地移除它们，保持队列单调递减

复杂度分析：

  • 时间复杂度：，每个元素最多入队和出队一次
  • 空间复杂度：，队列的大小

滑动窗口最小值

类似地，可以求滑动窗口的最小值，只需维护一个单调递增队列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from collections import deque

def minSlidingWindow(nums: List[int], k: int) -> List[int]:
    dq = deque()
    result = []
  
    for i in range(len(nums)):
        while dq and dq[0] <= i - k:
            dq.popleft()
      
        # 移除大于当前元素的元素
        while dq and nums[dq[-1]] > nums[i]:
            dq.pop()
      
        dq.append(i)
      
        if i >= k - 1:
            result.append(nums[dq[0]])
  
    return result

栈实现队列 / 队列实现栈

用栈实现队列（ LeetCode 232）

题目：请你仅使用两个栈实现先入先出队列。

思路：使用两个栈 stack_in 和 stack_out：

  • push：直接压入 stack_in
  • pop：如果 stack_out 为空，将 stack_in 的所有元素弹出并压入 stack_out，然后从 stack_out 弹出
  • peek：同 pop，但不删除元素
  • empty：两个栈都为空
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class MyQueue:
    def __init__(self):
        self.stack_in = []
        self.stack_out = []
  
    def push(self, x: int) -> None:
        self.stack_in.append(x)
  
    def pop(self) -> int:
        self.move()
        return self.stack_out.pop()
  
    def peek(self) -> int:
        self.move()
        return self.stack_out[-1]
  
    def empty(self) -> bool:
        return len(self.stack_in) == 0 and len(self.stack_out) == 0
  
    def move(self):
        # 如果 stack_out 为空，将 stack_in 的元素全部移到 stack_out
        if not self.stack_out:
            while self.stack_in:
                self.stack_out.append(self.stack_in.pop())

复杂度分析：

  • push：
  • pop：均摊 （每个元素最多移动一次）
  • peek：均摊
  • empty：

用队列实现栈（ LeetCode 225）

题目：请你仅使用两个队列实现一个后入先出（ LIFO）的栈。

思路一：两个队列 使用两个队列 queue1 和 queue2：

  • push：直接加入 queue1
  • pop：将 queue1 的前 n-1 个元素移到 queue2，弹出最后一个元素，然后交换 queue1 和 queue2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from collections import deque

class MyStack:
    def __init__(self):
        self.queue1 = deque()
        self.queue2 = deque()
  
    def push(self, x: int) -> None:
        self.queue1.append(x)
  
    def pop(self) -> int:
        while len(self.queue1) > 1:
            self.queue2.append(self.queue1.popleft())
        result = self.queue1.popleft()
        self.queue1, self.queue2 = self.queue2, self.queue1
        return result
  
    def top(self) -> int:
        return self.queue1[-1]
  
    def empty(self) -> bool:
        return len(self.queue1) == 0

思路二：一个队列 只用一个队列，push 时先加入新元素，然后将前面的元素依次出队再入队：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from collections import deque

class MyStack:
    def __init__(self):
        self.queue = deque()
  
    def push(self, x: int) -> None:
        self.queue.append(x)
        # 将前面的元素移到后面
        for _ in range(len(self.queue) - 1):
            self.queue.append(self.queue.popleft())
  
    def pop(self) -> int:
        return self.queue.popleft()
  
    def top(self) -> int:
        return self.queue[0]
  
    def empty(self) -> bool:
        return len(self.queue) == 0

复杂度分析：

  • push：（需要移动 个元素）
  • pop：
  • top：
  • empty：

时间空间复杂度分析

栈操作复杂度

操作 时间复杂度 空间复杂度
push
pop
peek
查找

队列操作复杂度

操作 时间复杂度 空间复杂度
enqueue
dequeue
peek
查找

优先队列（堆）操作复杂度

操作 时间复杂度 空间复杂度
插入
删除最小/最大
查找最小/最大
建堆

双端队列操作复杂度

操作 时间复杂度 空间复杂度
两端插入
两端删除
随机访问

常见算法复杂度总结

  1. 括号匹配： 时间， 空间
  2. 单调栈找下一个更大元素： 时间， 空间
  3. BFS 层次遍历： 时间（ 是节点数， 是边数）， 空间
  4. 滑动窗口最大值（单调队列）： 时间， 空间
  5. 前 K 个高频元素（堆）： 时间， 空间

❓ Q&A: 栈与队列常见问题

Q1: 什么时候用栈，什么时候用队列？

A:

  • 用栈：需要后进先出（ LIFO）的场景

    • 括号匹配、表达式求值
    • 函数调用、递归转迭代
    • 回溯算法（ DFS）
    • 单调栈优化

  • 用队列：需要先进先出（ FIFO）的场景

    • 层次遍历（ BFS）
    • 任务调度
    • 消息队列

Q2: 单调栈为什么能优化时间复杂度？

A: 单调栈利用了"如果当前元素满足某个条件（比如更大），那么它可能对之前未处理的元素也满足这个条件"的性质。通过维护单调性，避免了重复比较，将时间复杂度从 优化到 。

例如，在"下一个更大元素"问题中，如果当前元素比栈顶大，那么它一定比栈中所有比栈顶小的元素都大，因此可以一次性处理多个元素。

Q3: Python 中如何选择 list 和 deque？

A:

  • list：适合栈操作（append 和 pop 都是 ），但不适合队列（pop(0) 是 ）
  • deque：两端操作都是 ，适合队列和双端队列

对于队列，优先使用 deque；对于栈，list 和 deque 都可以，但 list 更常用。

Q4: 如何判断一个题目是否可以用单调栈？

A: 如果题目涉及：

  • "下一个更大/更小元素"
  • "左边第一个更大/更小元素"
  • "区间最值"
  • "满足某种单调性的子数组"

并且暴力解法是 ，可以考虑单调栈优化。

Q5: BFS 和 DFS 的区别是什么？

A:

  • BFS（广度优先搜索）：用队列实现，按层次遍历，适合找最短路径
  • DFS（深度优先搜索）：用栈（递归）实现，一条路走到底再回溯，适合找所有路径

BFS 的空间复杂度通常是 宽度， DFS 的空间复杂度是 深度。

Q6: 优先队列和普通队列的区别？

A:

  • 普通队列：先进先出，按插入顺序出队
  • 优先队列：按优先级出队，优先级高的先出（可以用最小堆或最大堆实现）

优先队列常用于：

  • Top K 问题
  • 合并多个有序序列
  • 任务调度（按优先级）

Q7: 为什么滑动窗口最大值用单调队列而不是优先队列？

A:

  • 优先队列：需要 时间删除窗口外的元素（需要查找），总时间复杂度
  • 单调队列：可以在 时间删除窗口外的元素（队首），总时间复杂度 单调队列通过维护单调性，避免了堆的额外开销。

Q8: 如何用栈实现递归？

A: 递归的本质就是函数调用栈。可以用显式栈模拟：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 递归版本
def dfs(node):
    if not node:
        return
    process(node)
    dfs(node.left)
    dfs(node.right)

# 迭代版本（用栈）
def dfs_iterative(root):
    stack = [root]
    while stack:
        node = stack.pop()
        if not node:
            continue
        process(node)
        stack.append(node.right)  # 注意顺序
        stack.append(node.left)

Q9: 什么时候需要两个栈/队列？

A:

  • 两个栈实现队列：需要将后进先出转换为先进先出
  • 两个队列实现栈：需要将先进先出转换为后进先出
  • 辅助栈：如最小栈问题，需要一个辅助栈记录额外信息

Q10: 如何优化栈/队列的空间复杂度？

A:

  1. 及时清理：处理完的元素及时出栈/出队
  2. 复用空间：如用两个栈实现队列时，可以复用 stack_out 的空间
  3. 延迟计算：如"下一个更大元素"，可以延迟到需要时才计算
  4. 使用索引：如果只需要索引信息，栈/队列中存储索引而不是完整对象

变体与扩展问题

变体一：多栈/多队列问题

有些问题需要同时维护多个栈或队列，或者在不同条件下使用不同的数据结构。

例题：用栈实现队列（ LeetCode 232）

需要两个栈：一个用于入队，一个用于出队。当出队栈为空时，将入队栈的所有元素转移到出队栈。

关键点：

  • move() 操作是均摊 的，因为每个元素最多移动一次
  • 只有在 stack_out 为空时才需要移动

变体二：单调栈的变种

单调栈不仅可以找"下一个更大元素"，还可以解决其他相关问题。

例题：去除重复字母（ LeetCode 316）

使用单调栈的思想，维护一个字典序最小的子序列。当遇到更小的字符且后面还有当前字符时，可以移除当前字符。

关键点：

  • 需要记录每个字符的剩余次数
  • 需要记录字符是否已经在栈中

变体三：优先队列的变种

优先队列不仅可以找 Top K，还可以解决其他优化问题。

例题：合并 K 个升序链表（ LeetCode 23）

使用最小堆，每次取出最小的节点，然后将其下一个节点入堆。

关键点：

  • 堆中需要存储 (值, 索引, 节点) 元组，避免节点无法比较的问题
  • 当某个链表遍历完时，不再将其节点入堆

常见错误与调试技巧

错误一：栈/队列为空时访问

问题：在栈/队列为空时调用 pop() 或 peek()，导致错误。

解决方法：

1
2
3
4
5
6
7
8
9
# 错误
val = stack.pop()  # 如果栈为空会报错

# 正确
if stack:
    val = stack.pop()
else:
    # 处理空栈情况
    pass

错误二：单调栈维护错误

问题：单调栈的单调性维护不当，导致结果错误。

解决方法：

  • 明确是单调递增还是单调递减
  • 明确是严格单调还是非严格单调
  • 检查弹出条件是否正确

错误三： BFS 中忘记标记已访问

问题：在 BFS 中，节点可能被重复加入队列。

解决方法：

1
2
3
4
5
6
7
8
9
10
visited = set()
queue.append(start)
visited.add(start)

while queue:
    node = queue.popleft()
    for neighbor in get_neighbors(node):
        if neighbor not in visited:
            visited.add(neighbor)
            queue.append(neighbor)

错误四：优先队列的比较函数错误

问题：在 Python 中使用 heapq 时，默认是最小堆。如果需要最大堆，需要取负数或使用自定义比较。

解决方法：

1
2
3
4
5
6
# 最小堆（默认）
heapq.heappush(heap, val)

# 最大堆（取负数）
heapq.heappush(heap, -val)
max_val = -heapq.heappop(heap)

调试技巧

  1. 打印栈/队列内容：
1
2
print(f"Stack: {stack}")
print(f"Queue: {list(queue)}")

  1. 跟踪操作序列：记录每次 push/pop 操作，验证逻辑正确性

  2. 使用可视化：对于复杂问题，画出栈/队列的变化过程

  3. 测试边界情况：

    • 空栈/空队列
    • 单个元素
    • 所有元素相同
    • 极端大小

实战建议

如何快速识别栈/队列问题

看到以下关键词时，考虑栈或队列：

  • 匹配问题：括号、标签匹配 → 栈
  • 表达式求值：中缀转后缀、后缀求值 → 栈
  • 层次遍历：树的层次遍历、图的 BFS → 队列
  • 下一个更大/更小：下一个更大元素 → 单调栈
  • 滑动窗口最值：滑动窗口最大值 → 单调队列
  • Top K：前 K 个高频元素 → 优先队列

选择数据结构的决策树

1
2
3
4
5
6
7
8
9
10
11
12
问题类型？
├─ 需要后进先出（ LIFO）→ 栈
│   ├─ 括号匹配 → 栈
│   ├─ 表达式求值 → 栈
│   └─ 单调栈优化 → 栈
├─ 需要先进先出（ FIFO）→ 队列
│   ├─ 层次遍历 → 队列
│   ├─ BFS → 队列
│   └─ 滑动窗口 → 双端队列
└─ 需要优先级 → 优先队列
    ├─ Top K → 堆
    └─ 合并有序序列 → 堆

解题步骤

  1. 识别问题类型：确定需要栈、队列还是其他数据结构
  2. 设计数据结构：确定需要存储什么信息（值、索引、状态等）
  3. 设计算法流程：明确入栈/入队、出栈/出队的时机
  4. 处理边界情况：空栈/空队列、单个元素等
  5. 优化：如果可能，进行时间或空间优化

性能优化建议

  1. 空间优化：

    • 及时清理不需要的元素
    • 使用索引代替完整对象
    • 复用数据结构空间

  2. 时间优化：

    • 使用更高效的数据结构（如 deque 代替 list）
    • 避免不必要的操作
    • 使用单调栈/队列优化查找

  3. 代码优化：

    • 合并相似逻辑
    • 使用更简洁的实现方式

总结

栈和队列是算法中最基础也最重要的数据结构。通过本文的学习，建议掌握：

  1. 基础操作：栈和队列的基本操作和实现
  2. 经典应用：括号匹配、表达式求值、最小栈等
  3. 单调栈：优化"下一个更大/更小元素"类问题
  4. BFS：用队列实现层次遍历和最短路径
  5. 优先队列：解决 Top K 问题和合并问题
  6. 双端队列：滑动窗口最值问题
  7. 相互实现：栈和队列的相互实现技巧

掌握这些知识点后，你就能解决 LeetCode 中大部分涉及栈和队列的题目。记住：多练习，多总结，理解每个数据结构的本质和应用场景，才能在面试中游刃有余。

  • 本文标题：LeetCode（十）—— 栈与队列
  • 本文作者：Chen Kai
  • 创建时间：2020-03-10 15:30:00
  • 本文链接：https://www.chenk.top/LeetCode%EF%BC%88%E5%8D%81%EF%BC%89%E2%80%94%E2%80%94-%E6%A0%88%E4%B8%8E%E9%98%9F%E5%88%97/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
 评论