LeetCode（六）—— 二叉树遍历与构造
Chen Kai BOSS
  2020-02-08 14:30:00 2020-02-08 14:30      6.8k 字  26 分钟  

二叉树是算法面试中的高频考点，从基础的遍历到复杂的构造问题，掌握二叉树的处理技巧是算法能力的重要体现。本文系统梳理二叉树的四种遍历方式（前序、中序、后序、层序），深入探讨递归与迭代两种实现方法，并通过经典构造问题（从前序中序构造、从后序中序构造）帮助读者建立完整的二叉树解题框架。我们还将分析复杂度、常见错误、优化技巧和变体扩展。

系列导航

📚 LeetCode 算法精讲系列（共 10 篇）：

  1. 哈希表（两数之和、最长连续序列、字母异位词分组）
  2. 双指针技巧（对撞指针、快慢指针、滑动窗口）
  3. 链表操作（反转、环检测、合并）
  4. 滑动窗口技巧
  5. 二分查找
  6. → 二叉树遍历与构造（前中后序、层序、构造）← 当前文章
  7. 动态规划入门（一维/二维 DP 、状态转移）
  8. 回溯算法（排列、组合、剪枝）
  9. 贪心算法（区间调度、跳跃游戏）
  10. 栈与队列（括号匹配、单调栈）

二叉树基础回顾

什么是二叉树？

二叉树（ Binary Tree）是每个节点最多有两个子节点的树结构。通常子节点被称为"左子节点"和"右子节点"。

核心特性：

  • 每个节点最多有两个子节点
  • 左子树和右子树是有序的（不能随意交换）
  • 空树也是二叉树

基本结构：

1
2
3
4
5
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

二叉树的分类

完全二叉树：除了最后一层，其他层节点都填满，最后一层从左到右填充。

满二叉树：所有层都完全填满的二叉树。

二叉搜索树（ BST）：对于每个节点，左子树所有节点值 < 节点值 < 右子树所有节点值。

平衡二叉树：左右子树高度差不超过 1 。

LeetCode 144: 二叉树的前序遍历

问题描述

给定一个二叉树的根节点 root，返回它的节点值的前序遍历。

前序遍历顺序：根节点 → 左子树 → 右子树

示例：

  • 输入：root = [1,null,2,3]
  • 输出：[1,2,3]

约束条件：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

问题分析

前序遍历的核心是先访问根节点，再递归处理左子树，最后递归处理右子树。这是最直观的遍历方式，因为总是先看到根节点的值。

应用场景：

  • 打印目录结构（先打印当前目录，再打印子目录）
  • 复制二叉树（先创建根节点，再复制子树）
  • 表达式树求值（先处理运算符，再处理操作数）

解题思路

递归思路：直接按照定义实现——先访问根，再递归左子树，最后递归右子树。

迭代思路：使用栈模拟递归过程。将根节点入栈，然后循环：弹出栈顶节点并访问，先压入右子节点，再压入左子节点（注意顺序，因为栈是后进先出）。

复杂度分析

  • 时间复杂度：，需要访问每个节点一次
  • 空间复杂度：
    • 递归：， 为树的高度（递归栈深度）
    • 迭代：，栈的最大深度为树的高度

递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
from typing import List, Optional

class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """
        前序遍历：根 -> 左 -> 右
        
        算法步骤：
        1. 如果根节点为空，返回空列表
        2. 访问根节点（添加到结果）
        3. 递归遍历左子树
        4. 递归遍历右子树
        
        边界条件：
        - 空树：直接返回 []
        - 单节点树：返回 [val]
        
        变量含义：
        - root: 当前子树的根节点
        - result: 存储遍历结果的列表
        """
        result = []
        
        def preorder(node):
            # 边界条件：空节点直接返回
            if not node:
                return
            
            # 步骤 1：访问根节点
            result.append(node.val)
            
            # 步骤 2：递归遍历左子树
            preorder(node.left)
            
            # 步骤 3：递归遍历右子树
            preorder(node.right)
        
        preorder(root)
        return result

算法原理：

前序遍历遵循"根-左-右"的顺序。递归实现利用了函数调用栈，当访问完左子树后，会自动返回到上一层继续处理右子树。

执行过程示例（树 [1, null, 2, 3]）：

1
2
3
4
5
6
7
8
9
访问节点 1 -> result = [1]
  递归左子树（ null）-> 直接返回
  递归右子树（节点 2）
    访问节点 2 -> result = [1, 2]
      递归左子树（节点 3）
        访问节点 3 -> result = [1, 2, 3]
          递归左子树（ null）
          递归右子树（ null）
      递归右子树（ null）

迭代实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    """
    迭代实现：使用栈模拟递归
    
    算法步骤：
    1. 初始化栈，将根节点入栈
    2. 当栈不为空时循环：
       a. 弹出栈顶节点并访问
       b. 如果右子节点存在，入栈
       c. 如果左子节点存在，入栈
    3. 返回结果
    
    关键技巧：
    - 先压右子节点，再压左子节点（因为栈是 LIFO）
    - 这样弹出时就是"根-左-右"的顺序
    
    边界条件：
    - 空树：栈为空，直接返回 []
    """
    if not root:
        return []
    
    result = []
    stack = [root]  # 初始化栈
    
    while stack:
        # 弹出栈顶节点
        node = stack.pop()
        result.append(node.val)  # 访问根节点
        
        # 先压右子节点，再压左子节点
        # 这样弹出时顺序是：左 -> 右（符合前序遍历）
        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)
    
    return result

为什么先压右后压左：

栈是后进先出（ LIFO）的数据结构。如果我们希望先访问左子树，就需要让左子节点后入栈，这样它就会先出栈。

执行过程示例（树 [1, null, 2, 3]）：

1
2
3
4
5
6
7
8
9
10
11
初始： stack = [1], result = []
迭代 1：弹出 1 -> result = [1]
       压入 2（右）-> stack = [2]
       压入 null（左，跳过）
迭代 2：弹出 2 -> result = [1, 2]
       压入 null（右，跳过）
       压入 3（左）-> stack = [3]
迭代 3：弹出 3 -> result = [1, 2, 3]
       压入 null（右，跳过）
       压入 null（左，跳过）
迭代 4： stack 为空，结束

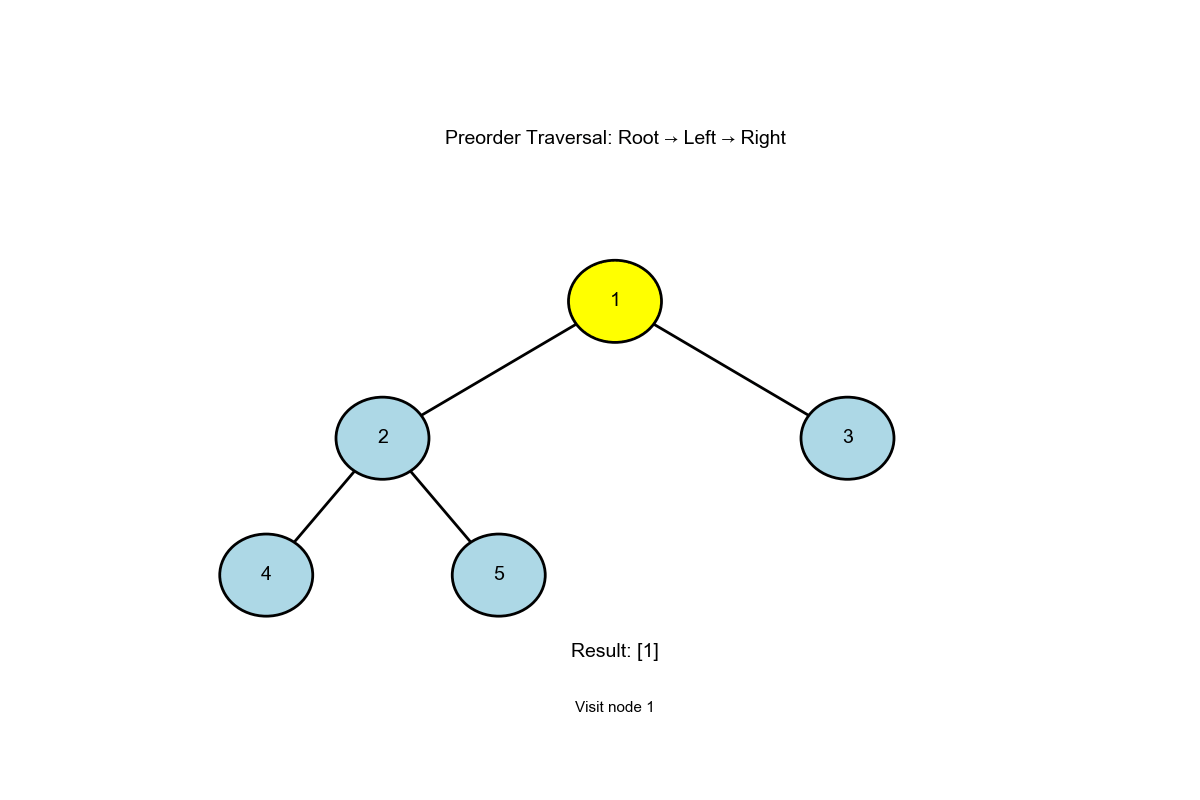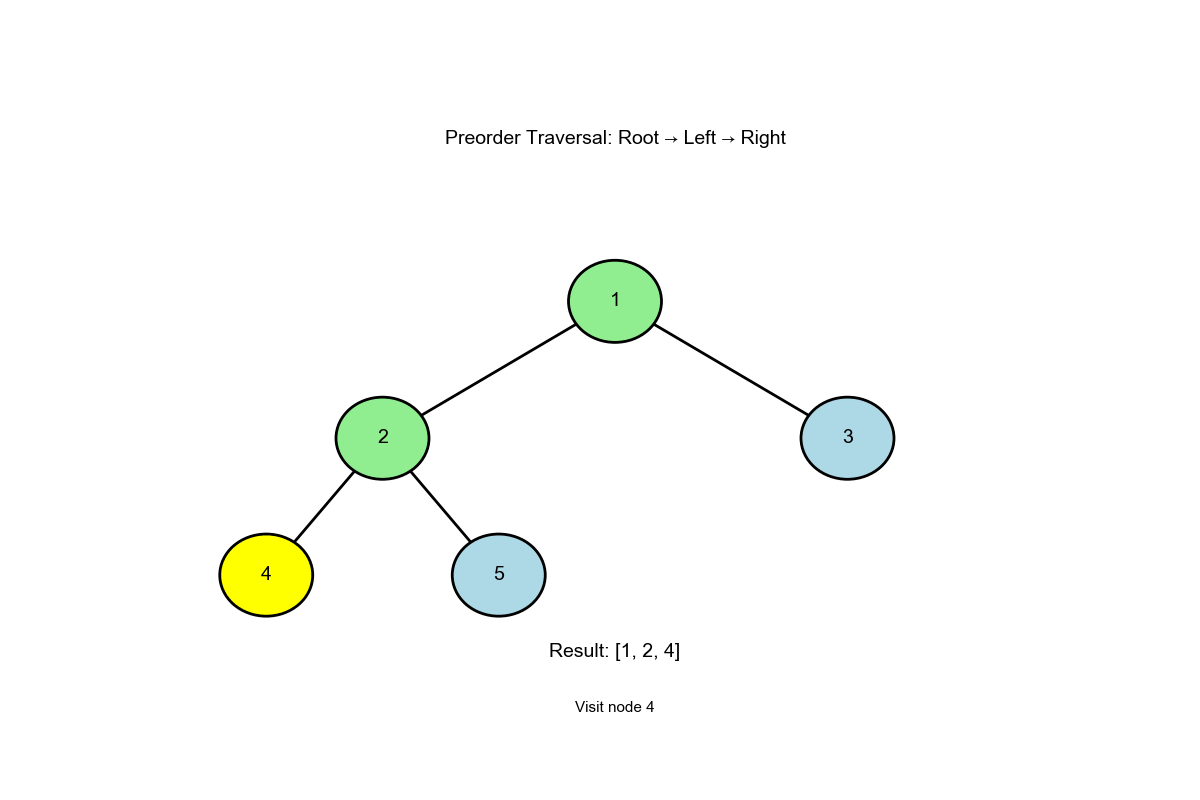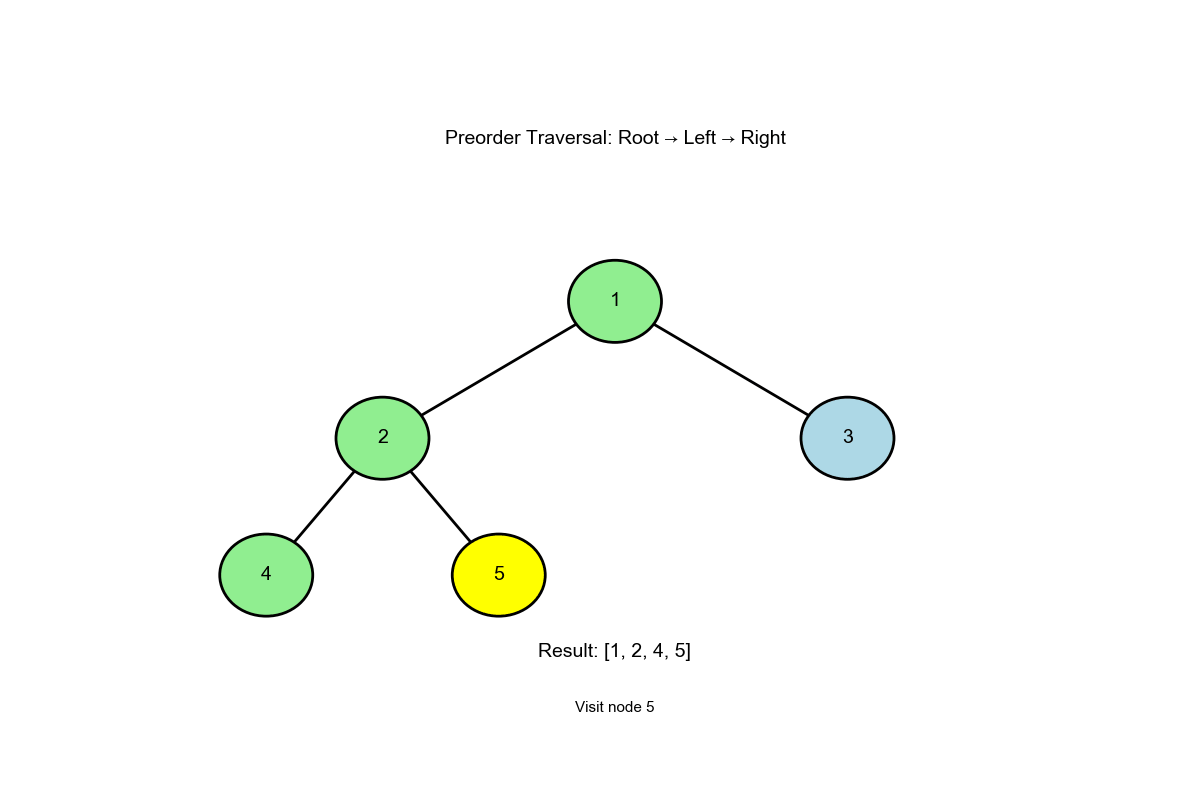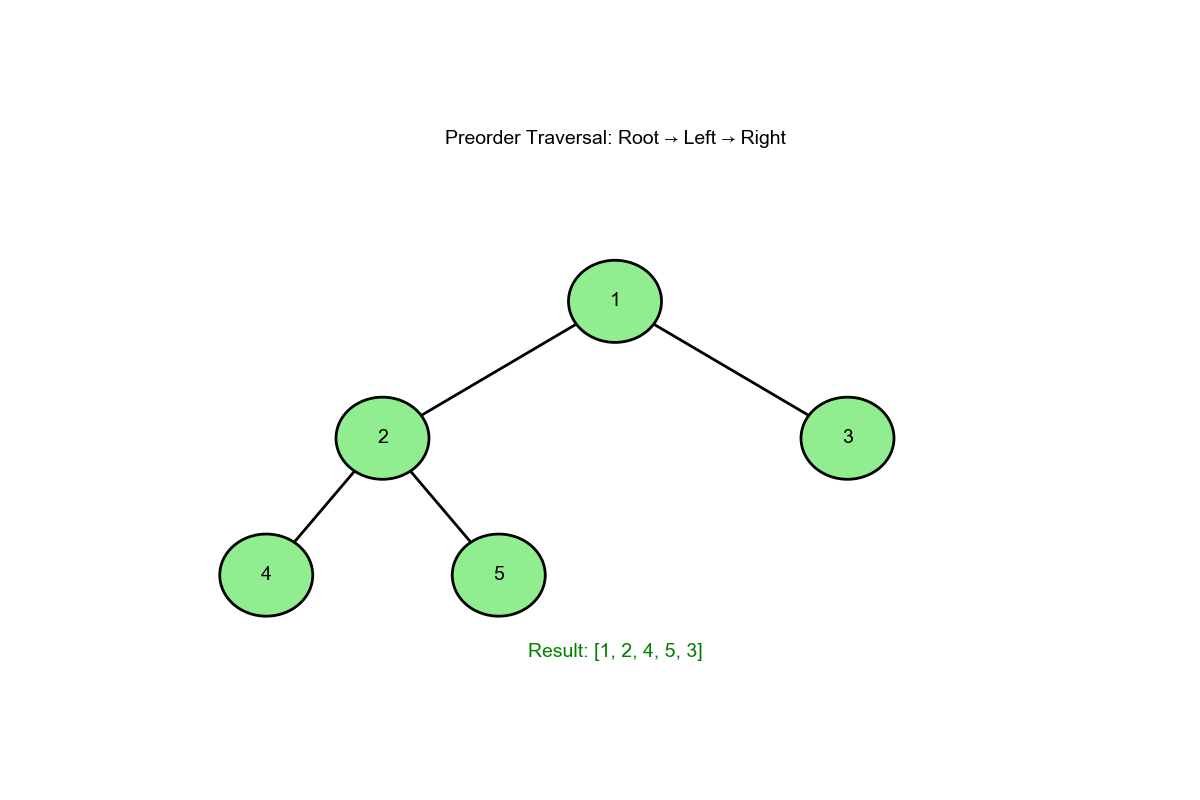
算法过程可视化：下面的动画演示了前序遍历如何按"根-左-右"顺序访问节点：

常见错误

错误一：忘记处理空节点

1
2
3
4
5
6
7
8
9
10
11
12
13
# ❌ 错误
def preorder(node):
    result.append(node.val)  # 如果 node 为 None 会报错
    preorder(node.left)
    preorder(node.right)

# ✅ 正确
def preorder(node):
    if not node:
        return
    result.append(node.val)
    preorder(node.left)
    preorder(node.right)

错误二：迭代实现中压栈顺序错误

1
2
3
4
5
6
7
8
9
10
11
12
# ❌ 错误：先压左后压右
if node.left:
    stack.append(node.left)
if node.right:
    stack.append(node.right)
# 这样会导致先访问右子树，顺序变成"根-右-左"

# ✅ 正确：先压右后压左
if node.right:
    stack.append(node.right)
if node.left:
    stack.append(node.left)

变体扩展

变体一： Morris 前序遍历（空间复杂度 ）

Morris 遍历利用树中的空指针，实现 空间复杂度的遍历：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def preorderTraversal_morris(self, root: Optional[TreeNode]) -> List[int]:
    """
    Morris 前序遍历： O(1)空间复杂度
    
    核心思想：利用叶子节点的空指针，建立临时链接
    当访问完左子树后，通过这个链接回到根节点
    """
    result = []
    current = root
    
    while current:
        if not current.left:
            # 没有左子树，直接访问当前节点
            result.append(current.val)
            current = current.right
        else:
            # 找到左子树的最右节点（前驱节点）
            predecessor = current.left
            while predecessor.right and predecessor.right != current:
                predecessor = predecessor.right
            
            if not predecessor.right:
                # 建立临时链接
                result.append(current.val)  # 访问根节点
                predecessor.right = current
                current = current.left
            else:
                # 临时链接已存在，说明左子树已访问完
                predecessor.right = None  # 恢复树结构
                current = current.right
    
    return result

复杂度分析：

  • 时间复杂度：，每个节点最多访问两次
  • 空间复杂度：，只使用常数额外空间

LeetCode 94: 二叉树的中序遍历

问题描述

给定一个二叉树的根节点 root，返回它的节点值的中序遍历。

中序遍历顺序：左子树 → 根节点 → 右子树

示例：

  • 输入：root = [1,null,2,3]
  • 输出：[1,3,2]

问题分析

中序遍历的特点是先处理左子树，再访问根节点，最后处理右子树。对于二叉搜索树（ BST），中序遍历的结果是有序的。

应用场景：

  • BST 有序输出：中序遍历 BST 得到升序序列
  • 表达式树求值：中序遍历表达式树得到中缀表达式
  • 验证 BST：检查中序遍历结果是否有序

解题思路

递归思路：先递归左子树，再访问根节点，最后递归右子树。

迭代思路：使用栈模拟递归。从根节点开始，一直向左走到底，将路径上的节点都入栈。然后弹出栈顶节点并访问，转向右子树，重复上述过程。

复杂度分析

  • 时间复杂度：
  • 空间复杂度：， 为树的高度

递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    """
    中序遍历：左 -> 根 -> 右
    
    算法步骤：
    1. 递归遍历左子树
    2. 访问根节点
    3. 递归遍历右子树
    """
    result = []
    
    def inorder(node):
        if not node:
            return
        
        inorder(node.left)      # 先处理左子树
        result.append(node.val)  # 再访问根节点
        inorder(node.right)     # 最后处理右子树
    
    inorder(root)
    return result

迭代实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    """
    迭代实现：使用栈模拟递归
    
    算法步骤：
    1. 从根节点开始，一直向左走到底，路径上的节点都入栈
    2. 弹出栈顶节点并访问
    3. 转向右子树，重复步骤 1
    
    关键技巧：
    - 使用 current 指针追踪当前节点
    - 当 current 为 None 且栈为空时，遍历结束
    """
    result = []
    stack = []
    current = root
    
    while current or stack:
        # 一直向左走到底
        while current:
            stack.append(current)
            current = current.left
        
        # 弹出栈顶节点（最左节点）
        current = stack.pop()
        result.append(current.val)  # 访问节点
        
        # 转向右子树
        current = current.right
    
    return result

执行过程示例（树 [1, null, 2, 3]）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
初始： current = 1, stack = [], result = []
迭代 1： current = 1，向左走到底
       入栈 1 -> stack = [1]
       current = null
       弹出 1 -> result = [1]
       current = 2（ 1 的右子节点）
迭代 2： current = 2，向左走到底
       入栈 2 -> stack = [2]
       current = 3（ 2 的左子节点）
       入栈 3 -> stack = [2, 3]
       current = null
       弹出 3 -> result = [1, 3]
       current = null（ 3 的右子节点）
       弹出 2 -> result = [1, 3, 2]
       current = null（ 2 的右子节点）
迭代 3： current = null, stack = []，结束

常见错误

错误：迭代实现中忘记转向右子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# ❌ 错误
while current or stack:
    while current:
        stack.append(current)
        current = current.left
    current = stack.pop()
    result.append(current.val)
    # 忘记： current = current.right
    # 会导致无限循环

# ✅ 正确
while current or stack:
    while current:
        stack.append(current)
        current = current.left
    current = stack.pop()
    result.append(current.val)
    current = current.right  # 必须转向右子树

LeetCode 145: 二叉树的后序遍历

问题描述

给定一个二叉树的根节点 root，返回它的节点值的后序遍历。

后序遍历顺序：左子树 → 右子树 → 根节点

示例：

  • 输入：root = [1,null,2,3]
  • 输出：[3,2,1]

问题分析

后序遍历的特点是先处理左右子树，最后访问根节点。这种顺序在删除树节点时很有用，因为需要先删除子节点才能删除父节点。

应用场景：

  • 删除二叉树：先删除子树，再删除根节点
  • 计算目录大小：先计算子目录大小，再计算总大小
  • 表达式树求值：后序遍历表达式树得到后缀表达式（逆波兰式）

解题思路

递归思路：先递归左子树，再递归右子树，最后访问根节点。

迭代思路：后序遍历的迭代实现较复杂。方法一：使用两个栈，先按"根-右-左"顺序入栈 1，再全部弹出到栈 2，最后依次弹出栈 2 得到"左-右-根"。方法二：使用一个栈，记录每个节点的访问状态（未访问、左子树已访问、右子树已访问）。

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    """
    后序遍历：左 -> 右 -> 根
    
    算法步骤：
    1. 递归遍历左子树
    2. 递归遍历右子树
    3. 访问根节点
    """
    result = []
    
    def postorder(node):
        if not node:
            return
        
        postorder(node.left)     # 先处理左子树
        postorder(node.right)    # 再处理右子树
        result.append(node.val)  # 最后访问根节点
    
    postorder(root)
    return result

迭代实现（双栈法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    """
    迭代实现：使用两个栈
    
    算法步骤：
    1. 使用栈 1 按"根-右-左"顺序遍历
    2. 将栈 1 弹出的节点压入栈 2
    3. 依次弹出栈 2，得到"左-右-根"顺序
    
    关键技巧：
    - 栈 1：根 -> 右 -> 左（前序遍历的镜像）
    - 栈 2：反转后得到 左 -> 右 -> 根（后序遍历）
    """
    if not root:
        return []
    
    stack1 = [root]
    stack2 = []
    
    while stack1:
        node = stack1.pop()
        stack2.append(node)  # 压入栈 2
        
        # 先压左，再压右（这样栈 2 弹出时是右->左，反转后是左->右）
        if node.left:
            stack1.append(node.left)
        if node.right:
            stack1.append(node.right)
    
    # 依次弹出栈 2
    result = []
    while stack2:
        result.append(stack2.pop().val)
    
    return result

为什么双栈法有效：

栈 1 按"根-右-左"顺序遍历（前序遍历的镜像），压入栈 2 后顺序不变。栈 2 弹出时顺序反转，得到"左-右-根"（后序遍历）。

迭代实现（单栈法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
    """
    迭代实现：使用一个栈，记录访问状态
    
    算法步骤：
    1. 使用栈存储(节点, 状态)元组
    2. 状态： 0=未访问， 1=左子树已访问， 2=右子树已访问
    3. 根据状态决定下一步操作
    """
    if not root:
        return []
    
    result = []
    stack = [(root, 0)]  # (节点, 状态)
    
    while stack:
        node, state = stack.pop()
        
        if state == 0:
            # 未访问：先访问左子树
            stack.append((node, 1))  # 标记为左子树已访问
            if node.left:
                stack.append((node.left, 0))
        elif state == 1:
            # 左子树已访问：访问右子树
            stack.append((node, 2))  # 标记为右子树已访问
            if node.right:
                stack.append((node.right, 0))
        else:
            # 右子树已访问：访问根节点
            result.append(node.val)
    
    return result

LeetCode 102: 二叉树的层序遍历

问题描述

给定一个二叉树的根节点 root，返回其节点值的层序遍历（即逐层地，从左到右访问所有节点）。

示例：

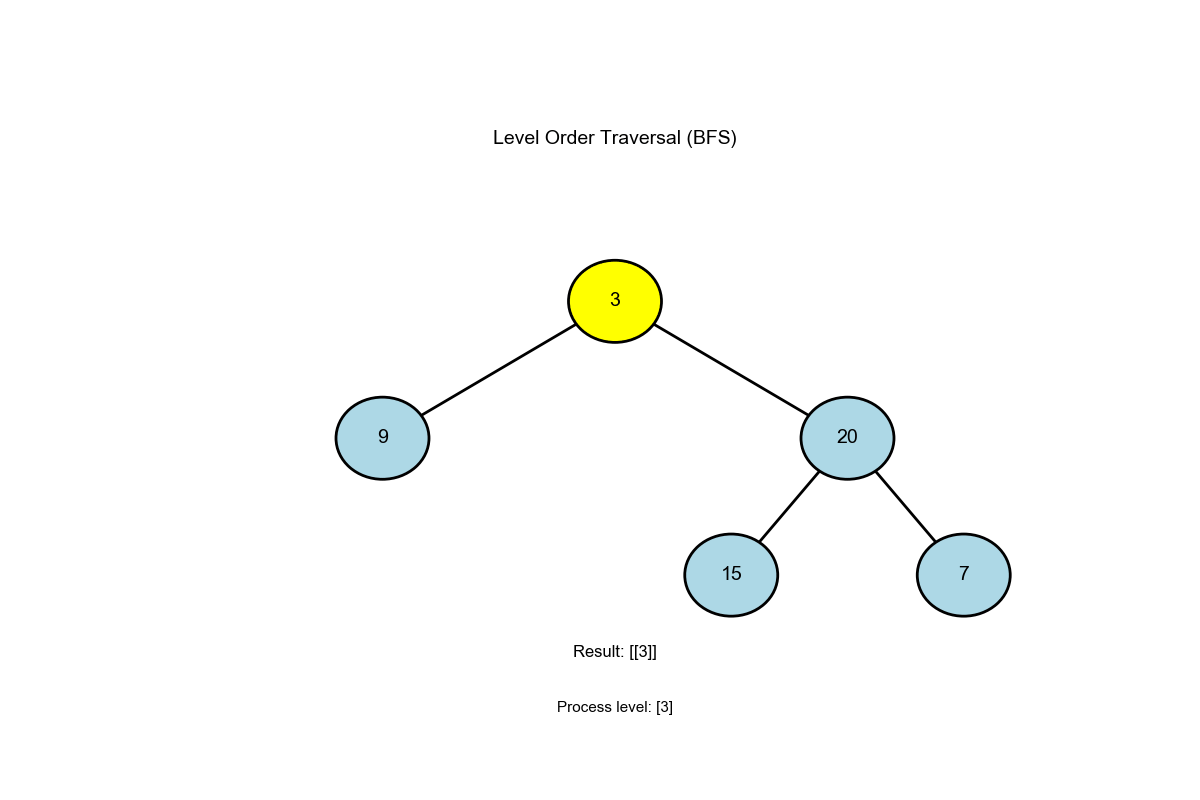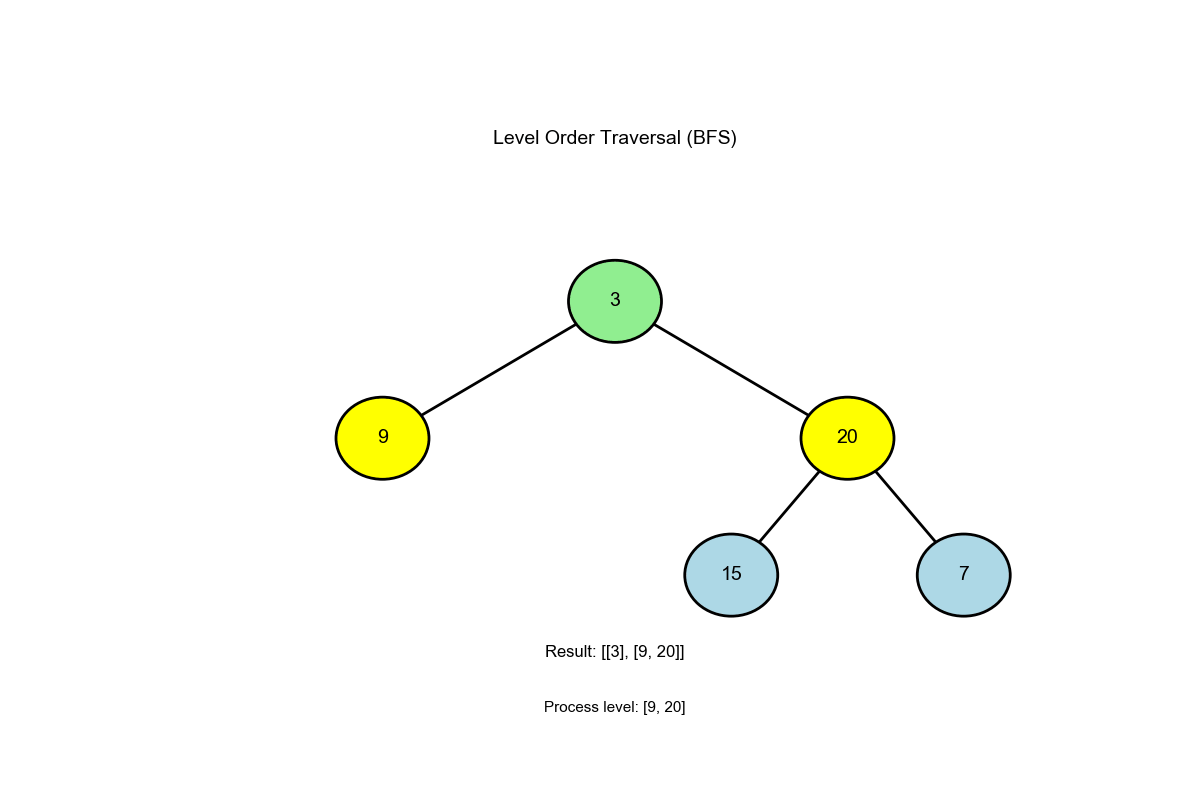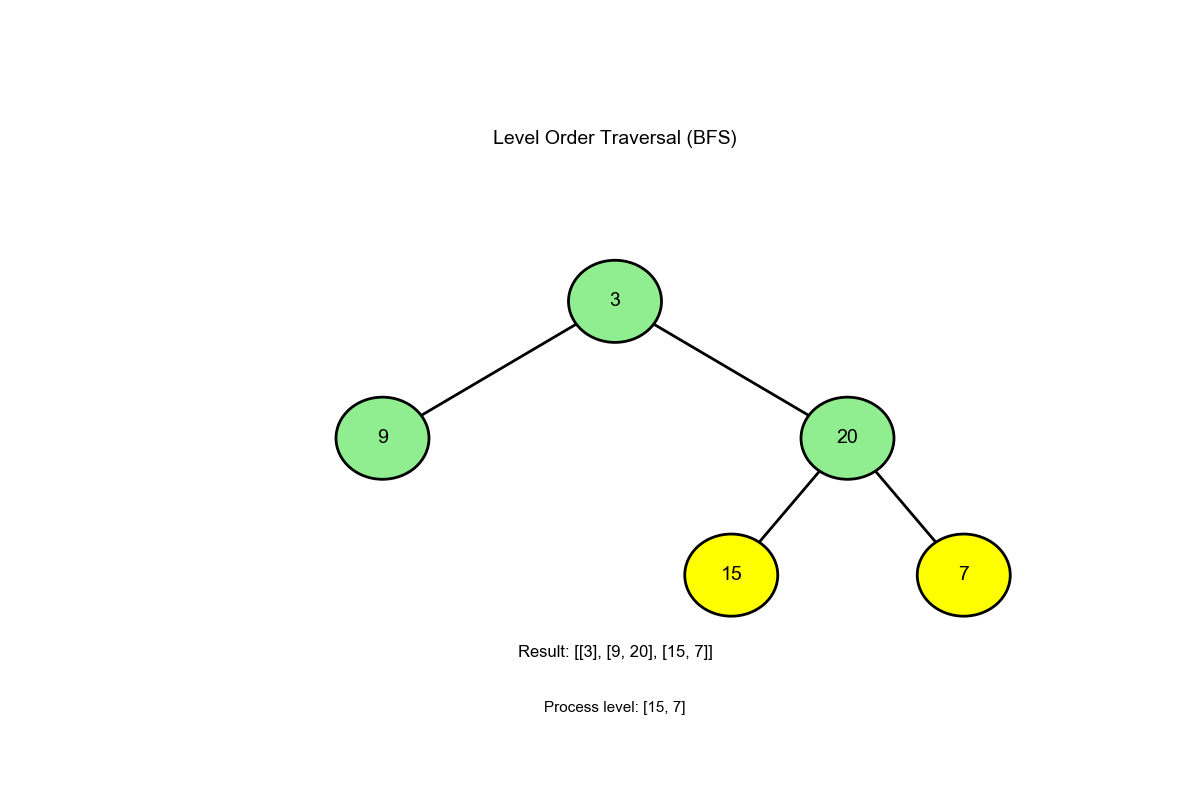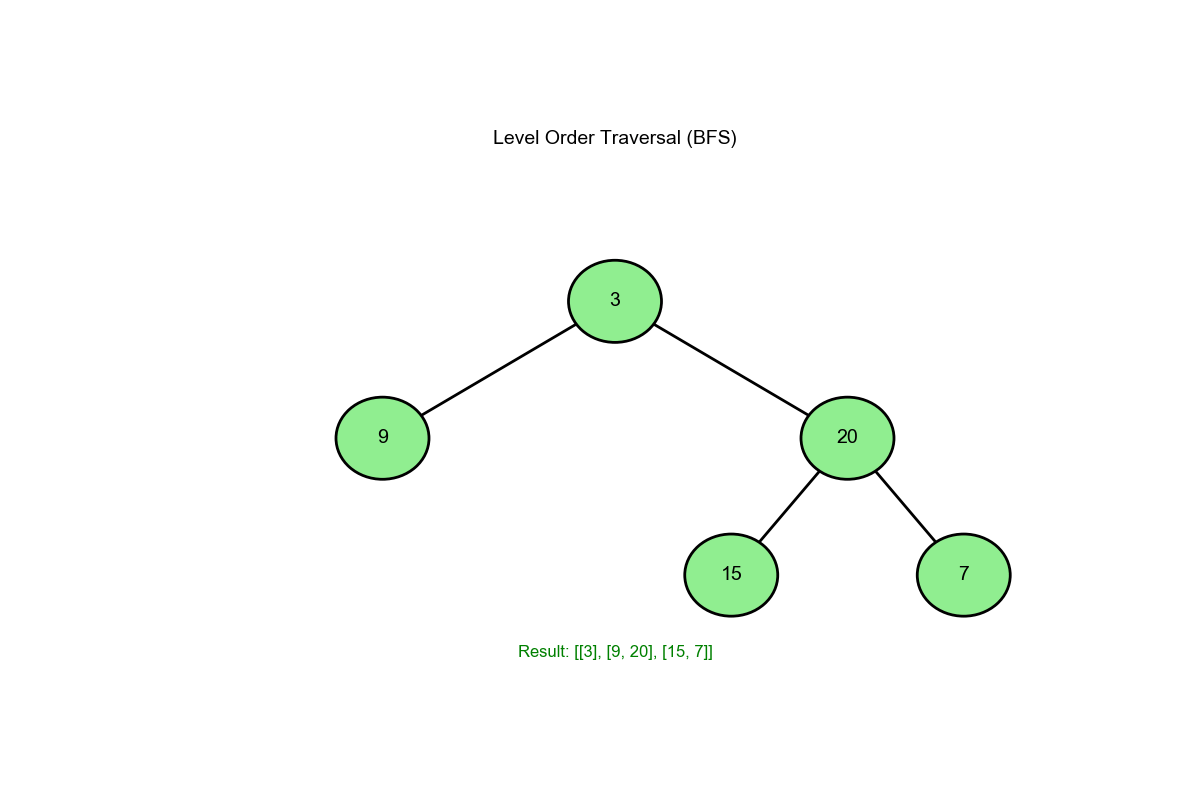
  • 输入：root = [3,9,20,null,null,15,7]
  • 输出：[[3],[9,20],[15,7]]

问题分析

层序遍历（ BFS）按照树的层级从上到下、从左到右访问节点。需要使用队列（ FIFO）来保证访问顺序。

应用场景：

  • 打印二叉树：按层级打印树结构
  • 找最短路径：在树中找从根到叶的最短路径
  • 序列化二叉树：按层级序列化树结构

解题思路

使用队列实现 BFS 。将根节点入队，然后循环：记录当前层的节点数，依次出队这些节点并访问，将它们的子节点入队。

复杂度分析

  • 时间复杂度：，每个节点访问一次
  • 空间复杂度：， 为树的最大宽度（队列的最大长度）

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
from collections import deque

def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
    """
    层序遍历：使用队列实现 BFS
    
    算法步骤：
    1. 将根节点入队
    2. 当队列不为空时循环：
       a. 记录当前层的节点数（队列长度）
       b. 依次出队这些节点，访问并收集到当前层结果
       c. 将出队节点的子节点入队
    3. 返回所有层的结果
    
    关键技巧：
    - 使用 level_size 记录每层节点数，确保分层处理
    - 子节点入队在下一轮循环中处理
    """
    if not root:
        return []
    
    result = []
    queue = deque([root])
    
    while queue:
        level_size = len(queue)  # 当前层的节点数
        level = []  # 当前层的结果
        
        # 处理当前层的所有节点
        for _ in range(level_size):
            node = queue.popleft()
            level.append(node.val)
            
            # 将子节点入队（下一层）
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        
        result.append(level)
    
    return result

执行过程示例（树 [3,9,20,null,null,15,7]）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
初始： queue = [3], result = []
第 1 层： level_size = 1
       出队 3 -> level = [3]
       入队 9, 20 -> queue = [9, 20]
       result = [[3]]
第 2 层： level_size = 2
       出队 9 -> level = [9]
       出队 20 -> level = [9, 20]
       入队 15, 7 -> queue = [15, 7]
       result = [[3], [9, 20]]
第 3 层： level_size = 2
       出队 15 -> level = [15]
       出队 7 -> level = [15, 7]
       无子节点入队
       result = [[3], [9, 20], [15, 7]]
结束： queue 为空

算法过程可视化：下面的动画演示了层序遍历如何逐层访问节点：

常见错误

错误：忘记记录层大小

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# ❌ 错误
while queue:
    node = queue.popleft()
    result.append(node.val)  # 没有分层，所有节点混在一起
    if node.left:
        queue.append(node.left)
    if node.right:
        queue.append(node.right)

# ✅ 正确
while queue:
    level_size = len(queue)  # 必须记录层大小
    level = []
    for _ in range(level_size):
        node = queue.popleft()
        level.append(node.val)
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)
    result.append(level)

LeetCode 105: 从前序与中序遍历序列构造二叉树

问题描述

给定两个整数数组 preorder 和 inorder，其中 preorder 是二叉树的先序遍历，inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例：

  • 输入：preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
  • 输出：[3,9,20,null,null,15,7]

约束条件：

  • preorder 和 inorder 均无重复元素

问题分析

核心洞察：

  1. 前序遍历的第一个元素是根节点
  2. 在中序遍历中找到根节点，左边是左子树，右边是右子树
  3. 递归构造左右子树

关键步骤：

  1. 从前序遍历中取第一个元素作为根节点
  2. 在中序遍历中找到根节点的位置
  3. 根据根节点位置，划分左右子树的范围
  4. 递归构造左子树和右子树

解题思路

使用递归 + 哈希表优化查找。哈希表存储中序遍历中每个值对应的索引，避免每次线性查找。

复杂度分析

  • 时间复杂度：，每个节点访问一次，哈希表查找
  • 空间复杂度：，哈希表 + 递归栈

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
    """
    从前序和中序遍历构造二叉树
    
    算法步骤：
    1. 创建哈希表，存储中序遍历中每个值的索引
    2. 递归函数 build(pre_start, pre_end, in_start, in_end)：
       a. 如果 pre_start > pre_end，返回 None
       b. 取 preorder[pre_start]作为根节点值
       c. 在 inorder 中找到根节点的位置 root_idx
       d. 计算左子树大小： left_size = root_idx - in_start
       e. 递归构造左子树： build(pre_start+1, pre_start+left_size, in_start, root_idx-1)
       f. 递归构造右子树： build(pre_start+left_size+1, pre_end, root_idx+1, in_end)
    
    边界条件：
    - 空数组： pre_start > pre_end
    - 单节点： pre_start == pre_end
    
    优化技巧：
    - 使用哈希表存储 inorder 索引，避免每次线性查找
    """
    # 创建哈希表：值 -> 索引
    inorder_map = {val: idx for idx, val in enumerate(inorder)}
    
    def build(pre_start, pre_end, in_start, in_end):
        # 边界条件：空子树
        if pre_start > pre_end:
            return None
        
        # 根节点值
        root_val = preorder[pre_start]
        root = TreeNode(root_val)
        
        # 在中序遍历中找到根节点位置
        root_idx = inorder_map[root_val]
        
        # 计算左子树大小
        left_size = root_idx - in_start
        
        # 递归构造左子树
        # 前序： pre_start+1 到 pre_start+left_size
        # 中序： in_start 到 root_idx-1
        root.left = build(
            pre_start + 1,
            pre_start + left_size,
            in_start,
            root_idx - 1
        )
        
        # 递归构造右子树
        # 前序： pre_start+left_size+1 到 pre_end
        # 中序： root_idx+1 到 in_end
        root.right = build(
            pre_start + left_size + 1,
            pre_end,
            root_idx + 1,
            in_end
        )
        
        return root
    
    return build(0, len(preorder) - 1, 0, len(inorder) - 1)

索引计算详解：

假设 preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]：

1
2
3
4
5
6
7
8
9
10
根节点： 3（ preorder[0]）
在 inorder 中位置： index=1

左子树：
  - 前序范围：[9]（ preorder[1:1+1]）
  - 中序范围：[9]（ inorder[0:1]）
  
右子树：
  - 前序范围：[20,15,7]（ preorder[2:5]）
  - 中序范围：[15,20,7]（ inorder[2:5]）

算法原理

为什么可以唯一确定二叉树：

前序遍历告诉我们根节点的位置，中序遍历告诉我们左右子树的划分。结合这两个信息，可以唯一确定树的结构。

数学证明：

对于 个节点的树，前序遍历有 种可能，中序遍历也有 种可能。但给定前序和中序，树的结构是唯一的（前提是节点值不重复）。

常见错误

错误一：索引计算错误

1
2
3
4
5
# ❌ 错误：左子树大小计算错误
left_size = root_idx  # 应该是 root_idx - in_start

# ✅ 正确
left_size = root_idx - in_start

错误二：忘记处理边界条件

1
2
3
4
5
6
7
8
9
# ❌ 错误
def build(pre_start, pre_end, in_start, in_end):
    root_val = preorder[pre_start]  # 如果 pre_start > pre_end 会越界
    
# ✅ 正确
def build(pre_start, pre_end, in_start, in_end):
    if pre_start > pre_end:
        return None
    root_val = preorder[pre_start]

LeetCode 106: 从后序与中序遍历序列构造二叉树

问题描述

给定两个整数数组 inorder 和 postorder，其中 inorder 是二叉树的中序遍历，postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

示例：

  • 输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
  • 输出：[3,9,20,null,null,15,7]

问题分析

核心洞察：

  1. 后序遍历的最后一个元素是根节点
  2. 在中序遍历中找到根节点，左边是左子树，右边是右子树
  3. 递归构造左右子树

与从前序构造的区别：根节点在后序遍历的末尾，而不是开头。

解题思路

类似前序+中序的构造方法，但根节点从后序遍历末尾取，右子树范围需要从后往前计算。

复杂度分析

  • 时间复杂度：
  • 空间复杂度：

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
    """
    从后序和中序遍历构造二叉树
    
    算法步骤：
    1. 创建哈希表存储 inorder 索引
    2. 递归函数 build(in_start, in_end, post_start, post_end)：
       a. 如果 post_start > post_end，返回 None
       b. 取 postorder[post_end]作为根节点值
       c. 在 inorder 中找到根节点位置 root_idx
       d. 计算右子树大小： right_size = in_end - root_idx
       e. 递归构造左子树和右子树
    
    关键区别：
    - 根节点在 postorder 末尾（ post_end）
    - 右子树范围从后往前计算
    """
    inorder_map = {val: idx for idx, val in enumerate(inorder)}
    
    def build(in_start, in_end, post_start, post_end):
        if post_start > post_end:
            return None
        
        # 根节点值（后序遍历最后一个）
        root_val = postorder[post_end]
        root = TreeNode(root_val)
        
        # 在中序遍历中找到根节点位置
        root_idx = inorder_map[root_val]
        
        # 计算右子树大小
        right_size = in_end - root_idx
        
        # 递归构造左子树
        # 中序： in_start 到 root_idx-1
        # 后序： post_start 到 post_end-right_size-1
        root.left = build(
            in_start,
            root_idx - 1,
            post_start,
            post_end - right_size - 1
        )
        
        # 递归构造右子树
        # 中序： root_idx+1 到 in_end
        # 后序： post_end-right_size 到 post_end-1
        root.right = build(
            root_idx + 1,
            in_end,
            post_end - right_size,
            post_end - 1
        )
        
        return root
    
    return build(0, len(inorder) - 1, 0, len(postorder) - 1)

遍历方式对比总结

遍历方式 顺序 递归实现难度 迭代实现难度 典型应用
前序遍历 根-左-右 ⭐ ⭐⭐ 复制树、打印目录
中序遍历 左-根-右 ⭐ ⭐⭐ BST 有序输出、验证 BST
后序遍历 左-右-根 ⭐ ⭐⭐⭐ 删除树、计算目录大小
层序遍历 从上到下、从左到右 ⭐⭐ ⭐⭐ 打印树、找最短路径

记忆口诀：

  • 前序：根在前（根-左-右）
  • 中序：根在中（左-根-右）
  • 后序：根在后（左-右-根）
  • 层序：按层来（ BFS）

❓ Q&A：二叉树遍历常见疑问

Q1：为什么中序遍历 BST 得到有序序列？

A： BST 的定义是：对于每个节点，左子树所有节点值 < 节点值 < 右子树所有节点值。

中序遍历的顺序是"左-根-右"，这意味着： 1. 先访问所有小于当前节点的值（左子树） 2. 再访问当前节点 3. 最后访问所有大于当前节点的值（右子树）

因此，中序遍历 BST 自然得到升序序列。

验证：

1
2
# BST: [4,2,6,1,3,5,7]
# 中序遍历：[1,2,3,4,5,6,7] ✅ 有序

Q2：迭代实现和递归实现哪个更好？

A：各有优劣：

维度 递归实现 迭代实现
代码简洁性 ✅ 更简洁 ❌ 更复杂
空间复杂度 ❌ （递归栈） ✅ （显式栈）
栈溢出风险 ❌ 深度大时可能溢出 ✅ 可控制
理解难度 ✅ 直观 ❌ 需要理解栈操作
性能 相当 相当

建议：

  • 面试：优先用递归（简洁），如果面试官要求迭代再改写
  • 生产：深度可控时用递归，深度很大时用迭代
  • 学习：两种都要掌握，理解本质

Q3：如何选择遍历方式？

A：根据问题需求选择：

前序遍历适用于： - 需要先处理根节点再处理子树 - 复制树结构 - 打印目录结构

中序遍历适用于： - BST 相关操作（查找、验证、有序输出） - 表达式树求中缀表达式

后序遍历适用于： - 需要先处理子树再处理根节点 - 删除树节点 - 计算目录大小 - 表达式树求后缀表达式

层序遍历适用于： - 需要按层级处理 - 找最短路径 - 序列化二叉树

Q4： Morris 遍历的优势是什么？

A： Morris 遍历的主要优势是空间复杂度 。

对比：

方法 空间复杂度 时间复杂度 适用场景
递归 一般情况
迭代+栈 一般情况
Morris 空间受限

代价：

  • 代码复杂度高
  • 会修改树结构（临时链接）
  • 不适合多线程环境

建议：除非空间限制严格，否则优先用递归或迭代实现。

Q5：构造二叉树时为什么需要中序遍历？

A：中序遍历提供了左右子树的划分信息。

为什么前序+后序不能唯一确定：

考虑两个不同的树：

1
2
3
树 1：     1         树 2：     1
        /                    \
       2                      2
  • 前序遍历都是：[1, 2]
  • 后序遍历都是：[2, 1]
  • 但树结构不同！

为什么前序+中序可以唯一确定：

  • 前序告诉我们根节点位置
  • 中序告诉我们左右子树划分
  • 结合两者可以唯一确定结构

数学证明：对于 个节点，给定前序和中序，树结构唯一（节点值不重复时）。

Q6：如何处理有重复值的二叉树？

A：有重复值时，构造可能不唯一。

问题：如果 preorder = [1,1,1], inorder = [1,1,1]，无法唯一确定树结构。

解决方案：

  1. 假设约束：题目通常保证节点值唯一
  2. 如果允许重复：需要额外信息（如节点 ID）来区分
  3. 实际应用：通常通过节点引用而非值来区分

Q7：层序遍历的时间复杂度为什么是 ？

A：每个节点恰好入队一次、出队一次。

分析：

  • 入队操作： 次（每个节点一次）
  • 出队操作： 次（每个节点一次）
  • 访问操作： 次（每个节点一次）

总操作数： 空间复杂度：队列最大长度为树的最大宽度 ，通常 $ w n，最坏情况（完全二叉树） w = n/2 $。

🎓 总结：二叉树遍历核心要点

记忆公式：

  • 前序：根 → 左 → 右
  • 中序：左 → 根 → 右
  • 后序：左 → 右 → 根
  • 层序： BFS，按层访问

记忆口诀：

前中后看根位置，层序就是 BFS

构造树需要中序，划分左右靠它来

实战 Checklist：

常见错误避免：

  • ✅ 递归时检查空节点
  • ✅ 迭代时注意压栈顺序
  • ✅ 层序遍历时记录层大小
  • ✅ 构造树时正确计算索引范围

通过系统掌握二叉树的遍历和构造，你就能解决大部分二叉树相关的 LeetCode 问题。记住：递归是基础，迭代是进阶，理解本质是关键！

  • 本文标题：LeetCode（六）—— 二叉树遍历与构造
  • 本文作者：Chen Kai
  • 创建时间：2020-02-08 14:30:00
  • 本文链接：https://www.chenk.top/LeetCode%EF%BC%88%E5%85%AD%EF%BC%89%E2%80%94%E2%80%94-%E4%BA%8C%E5%8F%89%E6%A0%91%E9%81%8D%E5%8E%86%E4%B8%8E%E6%9E%84%E9%80%A0/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
 评论