LeetCode（八）—— 回溯算法
Chen Kai BOSS
  2020-02-23 16:00:00 2020-02-23 16:00      13.7k 字  53 分钟  

回溯算法是解决组合优化问题的经典方法，在 LeetCode 中应用广泛。从全排列到 N 皇后，从子集生成到括号匹配，回溯算法以其清晰的递归结构和强大的搜索能力，成为解决这类问题的首选方案。本文将深入探讨回溯算法的核心思想、实现框架、优化技巧，并通过多个经典例题帮助读者掌握这一重要算法。

什么是回溯算法

回溯算法（ Backtracking）是一种通过探索所有可能的候选解来找出所有解的算法。当探索到某一步时，如果发现这个选择不能得到有效解，就回退一步，重新选择。回溯算法本质上是一种深度优先搜索（ DFS）的特殊形式，区别在于回溯算法会在搜索过程中撤销之前的选择。

回溯算法的核心思想可以用一句话概括：尝试所有可能的选择，如果当前选择不可行，就回退并尝试下一个选择。这种"试错"的过程，就像走迷宫时遇到死胡同就返回上一个路口重新选择路径一样。

回溯算法的历史可以追溯到 19 世纪，但真正系统化是在 20 世纪 50 年代。回溯算法特别适合解决约束满足问题（ Constraint Satisfaction Problems, CSP），这类问题的特点是：

  • 变量之间存在约束关系
  • 需要找到满足所有约束的解
  • 解的数量可能是指数级的

在计算机科学中，回溯算法被广泛应用于人工智能、编译器设计、组合数学等领域。在 LeetCode 中，回溯算法是解决排列、组合、子集等问题的标准方法。

回溯与 DFS 的关系

很多初学者会困惑：回溯算法和深度优先搜索（ DFS）有什么区别？实际上，回溯算法是 DFS 的一种应用形式。

DFS 是一种遍历图或树的算法，它沿着一条路径尽可能深地搜索，直到无法继续，然后回溯到上一个节点继续搜索。 DFS 的核心是遍历，目标是访问所有节点。

回溯算法 在 DFS 的基础上，增加了状态恢复的机制。当我们做出一个选择后，会递归地探索后续的可能性；当递归返回时，需要撤销这个选择，恢复到之前的状态，以便尝试其他选择。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# DFS 遍历树（不需要恢复状态）
def dfs(node):
    if node is None:
        return
    print(node.val)  # 访问节点
    dfs(node.left)
    dfs(node.right)

# 回溯算法（需要恢复状态）
def backtrack(path, choices):
    if 满足结束条件:
        记录结果
        return
    
    for choice in choices:
        path.append(choice)      # 做选择
        backtrack(path, choices) # 递归
        path.pop()               # 撤销选择（关键！）

回溯算法中的 path.pop() 就是状态恢复的关键。没有这一步，算法就无法正确地探索所有可能性。

实际应用场景对比

为了更好地理解两者的区别，我们看一个具体例子：

DFS 遍历二叉树：我们只需要访问每个节点一次，不需要恢复状态，因为每个节点的访问是独立的。

回溯解决全排列：需要尝试所有可能的排列。当我们选择数字 1 后，需要尝试选择 2 和 3；尝试完以 1 开头的所有排列后，需要"撤销"对 1 的选择，尝试选择 2，然后尝试以 2 开头的所有排列。这里的"撤销"就是状态恢复。

回溯算法的搜索树

回溯算法可以看作是在一棵隐式的搜索树上进行 DFS 。树的每个节点代表一个状态，边代表一个选择。当我们到达一个叶子节点时，如果满足条件，就找到了一个解；如果不满足，就回溯到父节点，尝试其他分支。

例如，对于全排列 [1,2,3]，搜索树的第一层有三个分支（选择 1 、 2 或 3），第二层有两个分支（选择剩余的两个数字之一），第三层只有一个分支（选择最后一个数字）。整个搜索树有 个叶子节点，对应 6 个排列。

回溯算法的三要素

理解回溯算法，需要掌握三个核心要素：选择（ Choice）、约束（ Constraint）、目标（ Goal）。

选择（ Choice）

选择是指在当前状态下，可以做出的所有可能决策。例如：

  • 在全排列问题中，选择是"选择哪个数字放在当前位置"
  • 在 N 皇后问题中，选择是"在当前位置放置皇后"
  • 在组合问题中，选择是"是否包含当前元素"

约束（ Constraint）

约束是指限制我们做出选择的条件。只有满足约束条件的选择才是合法的。例如：

  • 全排列中，不能选择已经使用过的数字
  • N 皇后中，不能与已有皇后在同一行、列或对角线上
  • 组合总和问题中，选择的数字之和不能超过目标值

目标（ Goal）

目标是指我们想要达到的终止条件。当满足目标时，我们就找到了一个解。例如：

  • 全排列中，当路径长度等于数组长度时，得到一个排列
  • N 皇后中，当成功放置 N 个皇后时，得到一个解
  • 子集问题中，当遍历完所有元素时，得到一个子集

回溯算法模板

回溯算法有一个通用的模板，掌握这个模板可以解决大部分回溯问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def backtrack(path, choices):
    # 终止条件：找到解或无法继续
    if 满足结束条件:
        结果.append(path[:])  # 注意：需要复制，不能直接 append(path)
        return
    
    # 遍历所有可能的选择
    for choice in choices:
        # 剪枝：跳过不满足约束的选择
        if 不满足约束条件:
            continue
        
        # 做选择
        path.append(choice)
        # 更新选择列表（如果需要）
        # new_choices = 更新后的选择列表
        
        # 递归
        backtrack(path, new_choices)
        
        # 撤销选择（回溯）
        path.pop()

关键点： 1. 结果保存：path[:] 创建了 path 的副本。如果直接 append(path)，由于 path 是引用，后续修改会影响已保存的结果。 2. 状态恢复：path.pop() 必须在递归返回后执行，确保回溯到上一个状态。 3. 剪枝优化：在循环中提前判断约束条件，避免无效递归。

模板的变体

根据问题的不同特点，模板会有一些变体：

变体一：需要返回值的回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def backtrack(path, choices):
    if 满足结束条件:
        return True  # 找到一个解就返回
    
    for choice in choices:
        if 不满足约束条件:
            continue
        
        path.append(choice)
        if backtrack(path, new_choices):  # 如果找到解，立即返回
            return True
        path.pop()
    
    return False  # 所有选择都尝试过，无解

变体二：需要记录路径的回溯

1
2
3
4
5
6
7
8
9
10
11
12
def backtrack(path, choices, result):
    if 满足结束条件:
        result.append(path[:])
        return
    
    for choice in choices:
        if 不满足约束条件:
            continue
        
        path.append(choice)
        backtrack(path, new_choices, result)
        path.pop()

变体三：使用索引而非列表拷贝

1
2
3
4
5
6
7
8
9
10
11
12
def backtrack(index, path):
    if index == len(nums):
        result.append(path[:])
        return
    
    # 选择 1：不包含当前元素
    backtrack(index + 1, path)
    
    # 选择 2：包含当前元素
    path.append(nums[index])
    backtrack(index + 1, path)
    path.pop()

LeetCode 46: 全排列

给定一个不含重复数字的数组 nums，返回其所有可能的全排列。可以按任意顺序返回答案。

示例：

  • 输入：nums = [1,2,3]
  • 输出：[[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]]

约束条件：

  • nums 中的所有整数互不相同
问题分析

全排列问题要求生成数组的所有排列方式。对于 个不同元素，共有 种排列。

核心挑战：

  1. 如何避免重复选择：每个元素在每个排列中只能出现一次
  2. 如何系统地探索所有可能性：需要尝试所有可能的排列组合
  3. 如何高效地回溯：当一条路径无法继续时，需要撤销选择并尝试其他路径

应用场景：

  • 密码破解：尝试所有可能的密码组合
  • 任务调度：安排任务的执行顺序
  • 游戏求解：探索所有可能的游戏状态

解题思路

回溯三要素分析：

  • 选择：当前位置可以选择哪些数字（所有未使用的数字）
  • 约束：不能选择已经使用过的数字（通过 used 数组标记）
  • 目标：路径长度等于数组长度（生成了一个完整排列）

算法流程：

  1. 使用 used 数组标记哪些数字已被使用
  2. 使用 path 列表记录当前路径（部分排列）
  3. 递归函数 backtrack()：
    • 如果 path 长度等于 nums 长度，保存结果并返回
    • 遍历所有数字，如果未使用，则：
      • 标记为已使用
      • 加入 path
      • 递归处理下一位置
      • 回溯：撤销标记和选择

复杂度分析

时间复杂度： - 共有 个排列（叶子节点数） - 每个排列需要 时间复制到结果中 - 总时间复杂度： 空间复杂度： - 递归栈深度：（最多 层递归） - path 数组： - used 数组： - 结果数组：（输出空间，不计入复杂度）

复杂度证明：

对于 个元素的全排列： - 第一层有 个选择 - 第二层有 个选择 - ... - 第 层有 个选择

总排列数： 每个排列需要 时间复制，因此总时间复杂度为 。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
from typing import List

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        """
        生成数组的所有全排列
        
        算法步骤：
        1. 初始化结果列表、路径列表和标记数组
        2. 定义回溯函数 backtrack()：
           a. 终止条件：路径长度等于数组长度，保存结果
           b. 遍历所有数字，跳过已使用的
           c. 做选择：标记使用、加入路径
           d. 递归：处理下一位置
           e. 撤销选择：恢复标记、移除路径
        
        边界条件：
        - 空数组：返回 [[]]
        - 单元素：返回 [[元素]]
        
        优化技巧：
        - 使用 used 数组避免重复选择（ O(1)查找）
        - 使用 path[:]创建副本保存结果（避免引用问题）
        
        变量含义：
        - result: 存储所有排列的结果列表
        - path: 当前正在构建的排列路径
        - used: 布尔数组， used[i]表示 nums[i]是否已使用
        """
        result = []
        path = []
        used = [False] * len(nums)  # 标记哪些数字已使用
        
        def backtrack():
            # 终止条件：路径长度等于数组长度
            if len(path) == len(nums):
                result.append(path[:])  # 创建副本，避免引用问题
                return
            
            # 遍历所有可能的选择
            for i in range(len(nums)):
                # 约束检查：跳过已使用的数字
                if used[i]:
                    continue
                
                # 做选择
                path.append(nums[i])
                used[i] = True
                
                # 递归：处理下一位置
                backtrack()
                
                # 撤销选择（回溯）
                path.pop()
                used[i] = False
        
        backtrack()
        return result

算法原理：

回溯算法通过"尝试-撤销"的方式系统地探索所有可能性：

  1. 尝试：选择一个未使用的数字加入当前路径
  2. 递归：继续构建剩余位置的排列
  3. 撤销：当递归返回时，撤销当前选择，尝试其他可能性

这种"深度优先搜索 + 状态恢复"的模式确保了所有排列都被探索到，且不会遗漏或重复。

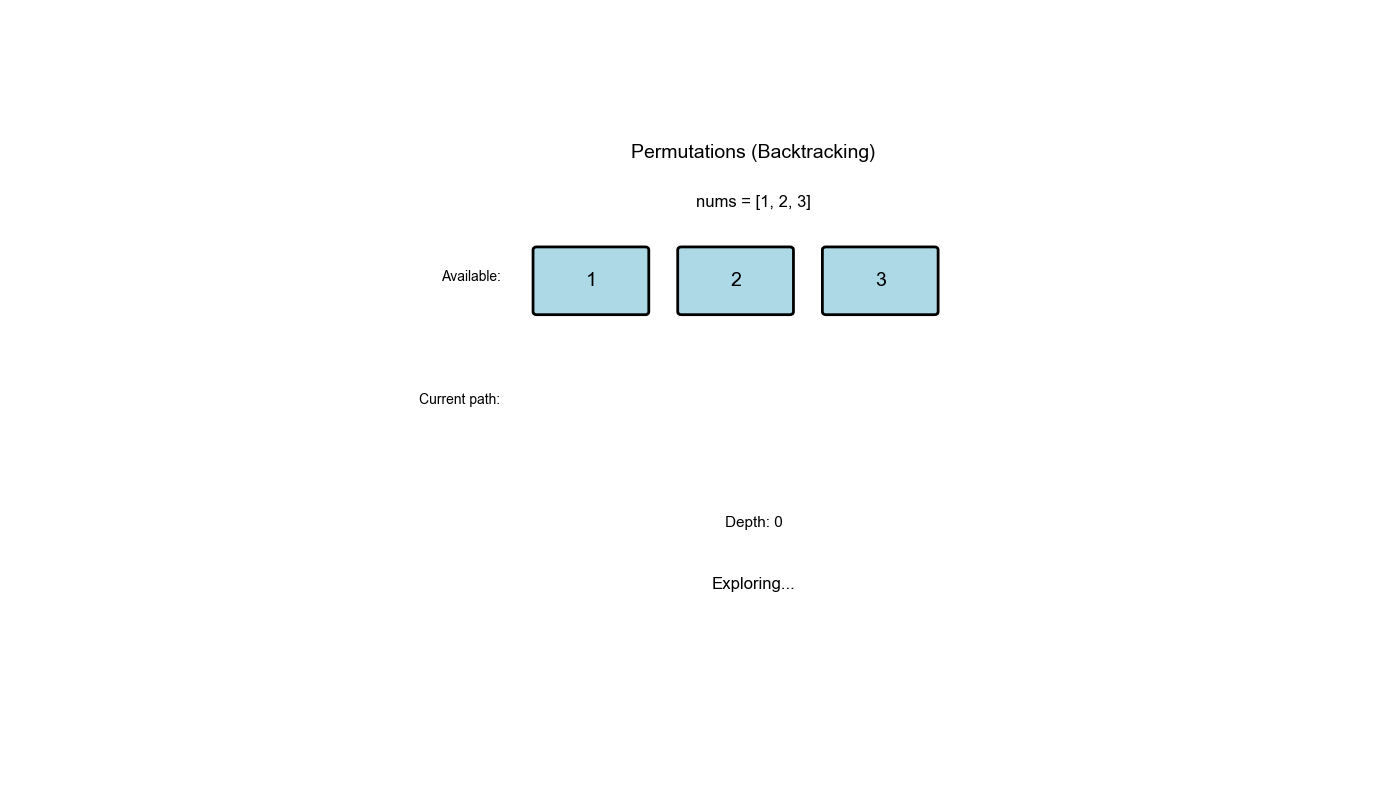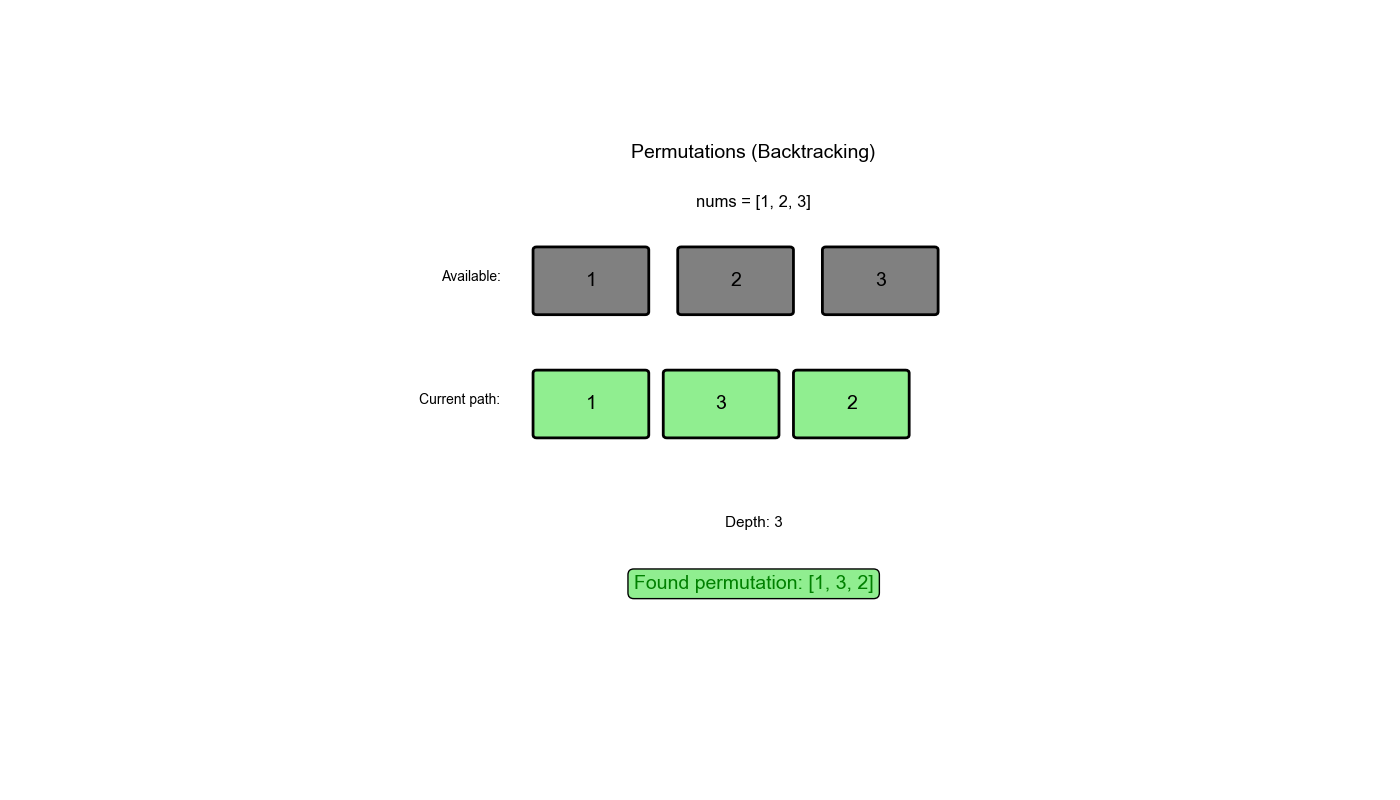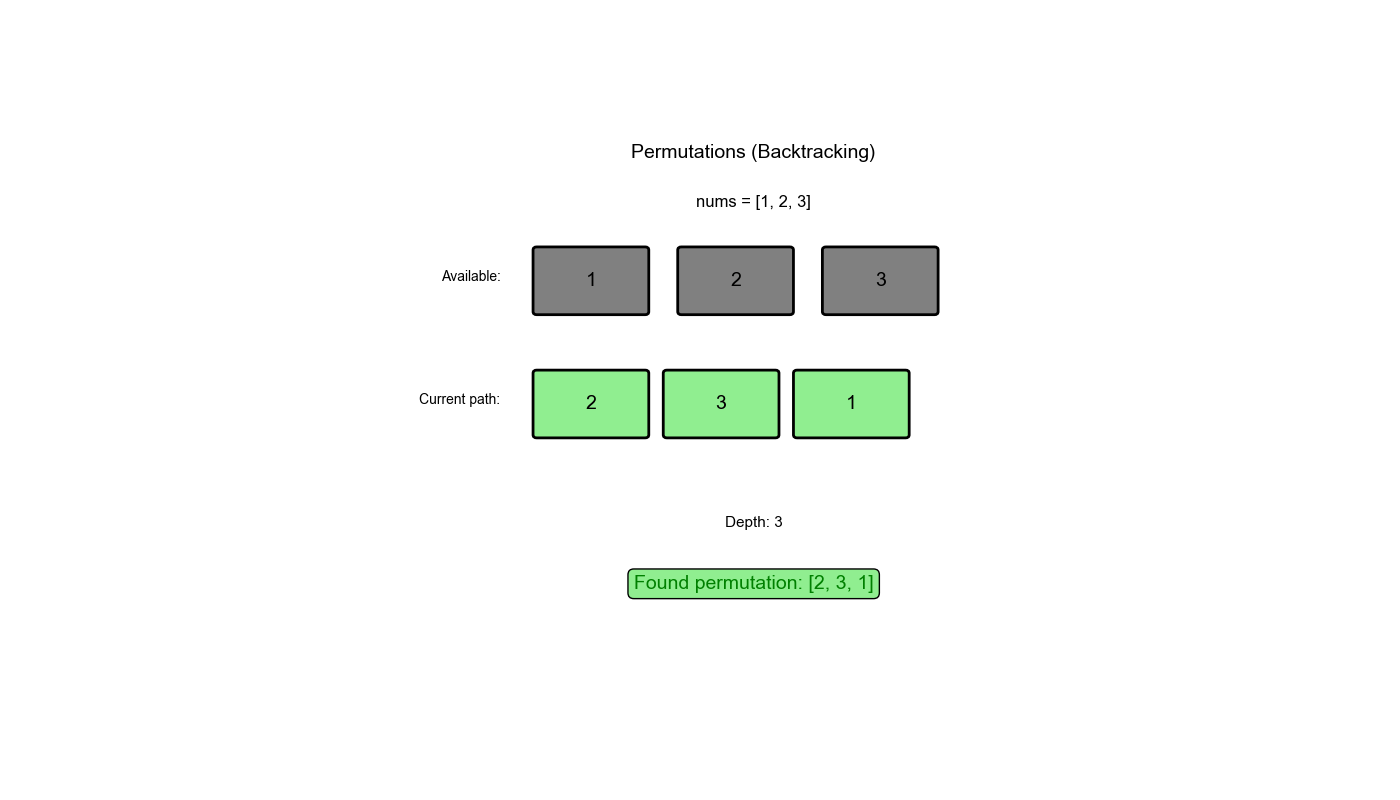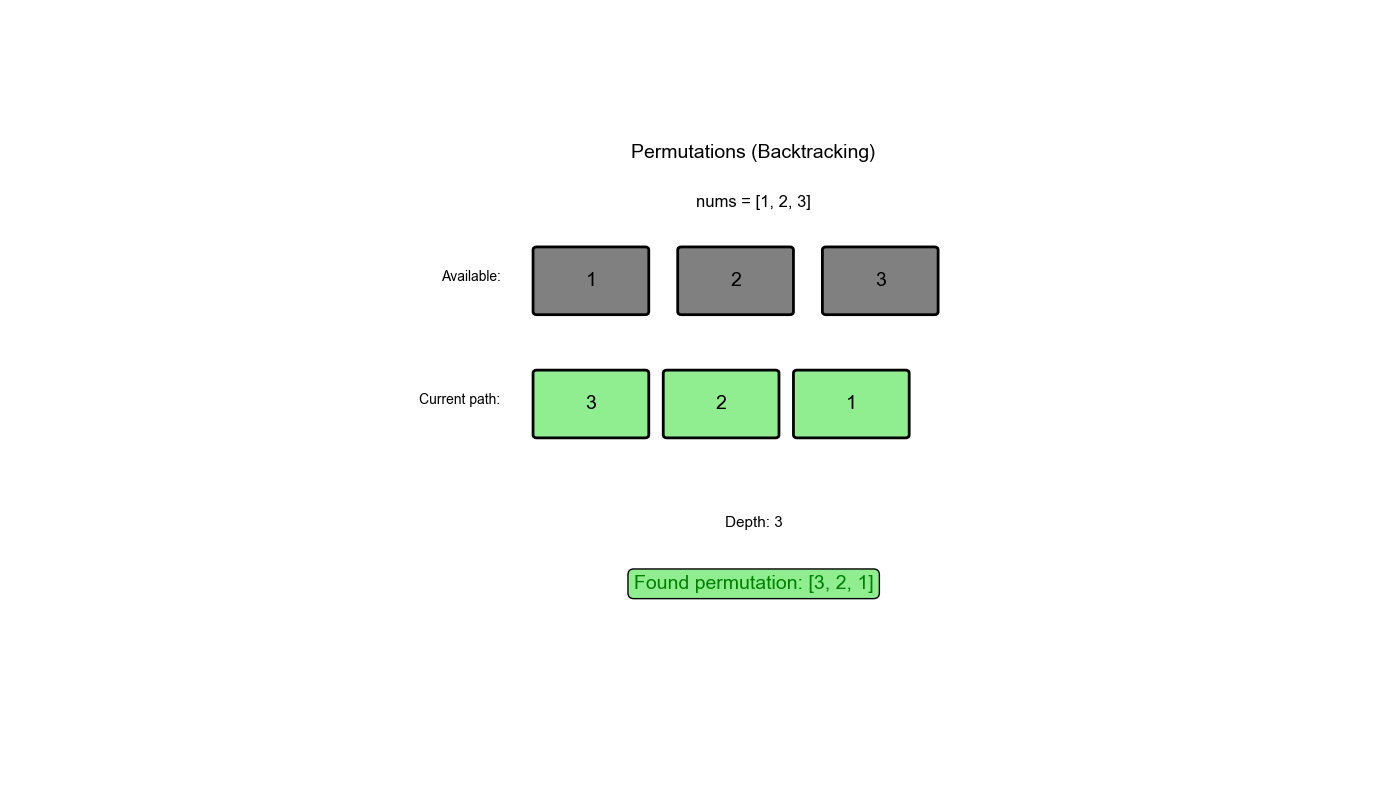
执行过程示例（nums = [1,2,3]）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
初始： path = [], used = [False, False, False]
第 1 层：选择 1
  path = [1], used = [True, False, False]
  第 2 层：选择 2
    path = [1,2], used = [True, True, False]
    第 3 层：选择 3
      path = [1,2,3] → 保存结果 [[1,2,3]]
      回溯： path = [1,2], used = [True, True, False]
    回溯： path = [1], used = [True, False, False]
  第 2 层：选择 3
    path = [1,3], used = [True, False, True]
    第 3 层：选择 2
      path = [1,3,2] → 保存结果 [[1,2,3], [1,3,2]]
      回溯： path = [1,3], used = [True, False, True]
    回溯： path = [1], used = [True, False, False]
  回溯： path = [], used = [False, False, False]
第 1 层：选择 2（继续类似过程）...

常见错误：

错误一：忘记创建路径副本

1
2
3
4
5
# ❌ 错误
result.append(path)  # path 是引用，后续修改会影响已保存的结果

# ✅ 正确
result.append(path[:])  # 创建副本

错误二：忘记撤销选择

1
2
3
4
5
6
7
8
9
10
11
12
13
# ❌ 错误
path.append(nums[i])
used[i] = True
backtrack()
# 忘记： path.pop() 和 used[i] = False
# 导致无法回溯，无法探索其他可能性

# ✅ 正确
path.append(nums[i])
used[i] = True
backtrack()
path.pop()      # 必须撤销
used[i] = False  # 必须恢复状态

错误三：约束检查位置错误

1
2
3
4
5
6
7
8
9
10
11
# ❌ 错误：在递归后检查约束
path.append(nums[i])
backtrack()
if used[i]:  # 太晚了！
    continue

# ✅ 正确：在递归前检查约束
if used[i]:
    continue
path.append(nums[i])
backtrack()

全排列问题的搜索过程

让我们追踪一下 permute([1,2,3]) 的执行过程：

  1. 初始状态：path = [], used = [False, False, False]

  2. 第一层递归：选择 1

    • path = [1], used = [True, False, False]
    • 第二层递归：选择 2
      • path = [1,2], used = [True, True, False]
      • 第三层递归：选择 3
        • path = [1,2,3] → 满足条件，保存结果
        • 回溯：path = [1,2], used = [True, True, False]
      • 回溯：path = [1], used = [True, False, False]
    • 第二层递归：选择 3
      • path = [1,3], used = [True, False, True]
      • 第三层递归：选择 2
        • path = [1,3,2] → 满足条件，保存结果

  3. 回溯到第一层：path = [], used = [False, False, False]

  4. 第一层递归：选择 2（继续类似过程）...

通过这个过程回溯算法系统地探索了所有 种可能性。

全排列 II（包含重复元素）

如果数组包含重复元素，需要去重。有两种方法：

方法一：排序 + 剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def permuteUnique(nums):
    result = []
    path = []
    nums.sort()  # 排序，使相同元素相邻
    used = [False] * len(nums)
    
    def backtrack():
        if len(path) == len(nums):
            result.append(path[:])
            return
        
        for i in range(len(nums)):
            if used[i]:
                continue
            # 剪枝：如果当前数字与前一个相同，且前一个未使用，则跳过
            # 这确保了相同数字的相对顺序，避免重复
            if i > 0 and nums[i] == nums[i-1] and not used[i-1]:
                continue
            
            path.append(nums[i])
            used[i] = True
            backtrack()
            path.pop()
            used[i] = False
    
    backtrack()
    return result

方法二：使用集合去重

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def permuteUnique(nums):
    result = []
    path = []
    used = [False] * len(nums)
    
    def backtrack():
        if len(path) == len(nums):
            result.append(path[:])
            return
        
        seen = set()  # 当前层已使用的数字
        for i in range(len(nums)):
            if used[i] or nums[i] in seen:
                continue
            seen.add(nums[i])
            
            path.append(nums[i])
            used[i] = True
            backtrack()
            path.pop()
            used[i] = False
    
    backtrack()
    return result

LeetCode 39: 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。

示例：

  • 输入：candidates = [2,3,6,7], target = 7
  • 输出：[[2,2,3], [7]]

约束条件：

  • candidates 中的所有元素互不相同

问题分析

组合总和问题要求找到所有和为 target 的组合，且每个数字可以重复使用。

核心挑战：

  1. 如何避免重复组合：[2,3] 和 [3,2] 是同一个组合，需要避免重复
  2. 如何控制搜索空间：当剩余值小于 0 时，需要提前终止
  3. 如何允许重复使用：同一个数字可以在组合中出现多次

关键洞察：

通过限制选择范围（从 start 开始）来避免重复。如果总是从数组开头选择，会产生 [2,3] 和 [3,2] 这样的重复组合。通过只从当前位置及之后选择，确保组合中的数字按数组顺序排列，从而避免重复。

解题思路

回溯三要素分析：

  • 选择：选择哪个数字加入当前组合（从 start 位置开始）
  • 约束：
    • 组合的和不能超过 target（remain >= 0）
    • 只能从当前位置及之后选择（避免重复）
  • 目标：组合的和等于 target（remain == 0）

算法流程：

  1. 定义回溯函数 backtrack(start, remain)：
    • start：当前可以选择的位置起始索引
    • remain：剩余目标和
  2. 终止条件：
    • remain == 0：找到有效组合，保存结果
    • remain < 0：当前路径无效，直接返回
  3. 遍历从 start 开始的所有候选数字：
    • 加入当前路径
    • 递归：backtrack(i, remain - candidates[i])（注意从 i 开始，允许重复）
    • 回溯：移除当前选择

复杂度分析

时间复杂度：，其中 - 最坏情况下，每个位置都有两个选择（选或不选） - 由于可以重复选择，实际搜索空间可能更大 - 通过剪枝可以大幅减少实际搜索节点数

空间复杂度： - 递归栈深度最多为 target（当每次都选择最小数字时） - path 数组长度最多为 target

复杂度证明：

假设最小候选数为 ，则最多需要选择 个数字。每个位置有 个选择，但由于剪枝和重复使用的限制，实际复杂度介于 和 之间，其中 。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
from typing import List

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        """
        找出所有和为 target 的组合（数字可重复使用）
        
        算法步骤：
        1. 定义回溯函数 backtrack(start, remain)：
           a. 终止条件 1： remain == 0，保存结果
           b. 终止条件 2： remain < 0，剪枝返回
           c. 从 start 开始遍历候选数字
           d. 做选择：加入路径
           e. 递归： backtrack(i, remain - candidates[i])（从 i 开始，允许重复）
           f. 撤销选择：移除路径
        
        边界条件：
        - 空数组：返回 []
        - target 为 0：返回 [[]]
        - 所有候选数都大于 target：返回 []
        
        优化技巧：
        - 使用 start 参数避免重复组合（只从当前位置及之后选择）
        - remain < 0 时提前剪枝，减少无效搜索
        - 排序后可以进一步优化（见下方优化版本）
        
        变量含义：
        - result: 存储所有有效组合的结果列表
        - path: 当前正在构建的组合路径
        - start: 当前可以选择的位置起始索引（避免重复）
        - remain: 剩余目标和
        """
        result = []
        path = []
        
        def backtrack(start, remain):
            # 终止条件 1：找到有效组合
            if remain == 0:
                result.append(path[:])  # 保存结果
                return
            
            # 终止条件 2：当前路径无效（剪枝）
            if remain < 0:
                return
            
            # 从 start 开始选择，避免重复组合
            for i in range(start, len(candidates)):
                # 做选择
                path.append(candidates[i])
                
                # 递归：注意从 i 开始（不是 i+1），允许重复使用
                backtrack(i, remain - candidates[i])
                
                # 撤销选择（回溯）
                path.pop()
        
        backtrack(0, target)
        return result

算法原理：

为什么从 start 开始可以避免重复：

假设 candidates = [2,3,6,7]，target = 7：

  • 如果从 0 开始：可能产生 [2,3] 和 [3,2]（重复）
  • 如果从 start 开始：
    • 选择 2 后，start=0，只能选择 2,3,6,7 → 产生 [2,2,3], [2,3] 等
    • 选择 3 后，start=1，只能选择 3,6,7 → 产生 [3,3] 等
    • 不会产生 [3,2]，因为选择 3 时 start=1，不会再选择 2

为什么递归时从 i 开始（不是 i+1）：

因为题目允许重复使用同一个数字。如果从 i+1 开始，每个数字只能使用一次，就变成了"组合总和 II"问题。

常见错误：

错误一：从 0 开始选择导致重复

1
2
3
4
5
6
7
8
# ❌ 错误
for i in range(len(candidates)):  # 总是从 0 开始
    backtrack(i, remain - candidates[i])
# 会产生 [2,3] 和 [3,2] 这样的重复组合

# ✅ 正确
for i in range(start, len(candidates)):  # 从 start 开始
    backtrack(i, remain - candidates[i])

错误二：递归时使用 i+1 导致无法重复使用

1
2
3
4
5
# ❌ 错误
backtrack(i + 1, remain - candidates[i])  # 每个数字只能用一次

# ✅ 正确
backtrack(i, remain - candidates[i])  # 允许重复使用

组合总和问题的优化

可以通过排序和提前终止来优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def combinationSum(candidates, target):
    result = []
    path = []
    candidates.sort()  # 排序，便于剪枝
    
    def backtrack(start, remain):
        if remain == 0:
            result.append(path[:])
            return
        
        for i in range(start, len(candidates)):
            # 剪枝：如果当前数字已经大于剩余值，后续数字更大，直接返回
            if candidates[i] > remain:
                break  # 注意是 break 不是 continue，因为已排序
            
            path.append(candidates[i])
            backtrack(i, remain - candidates[i])
            path.pop()
    
    backtrack(0, target)
    return result

这个优化利用了排序的性质：如果 candidates[i] > remain，那么 candidates[i+1] 及之后的数字都大于 remain，可以直接终止循环。

组合总和 II（每个数字只能使用一次）

如果每个数字只能使用一次，且数组可能包含重复元素：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def combinationSum2(candidates, target):
    result = []
    path = []
    candidates.sort()  # 排序以便去重
    
    def backtrack(start, remain):
        if remain == 0:
            result.append(path[:])
            return
        if remain < 0:
            return
        
        for i in range(start, len(candidates)):
            # 剪枝：跳过重复元素
            if i > start and candidates[i] == candidates[i-1]:
                continue
            
            path.append(candidates[i])
            # 每个数字只能用一次，所以从 i+1 开始
            backtrack(i + 1, remain - candidates[i])
            path.pop()
    
    backtrack(0, target)
    return result

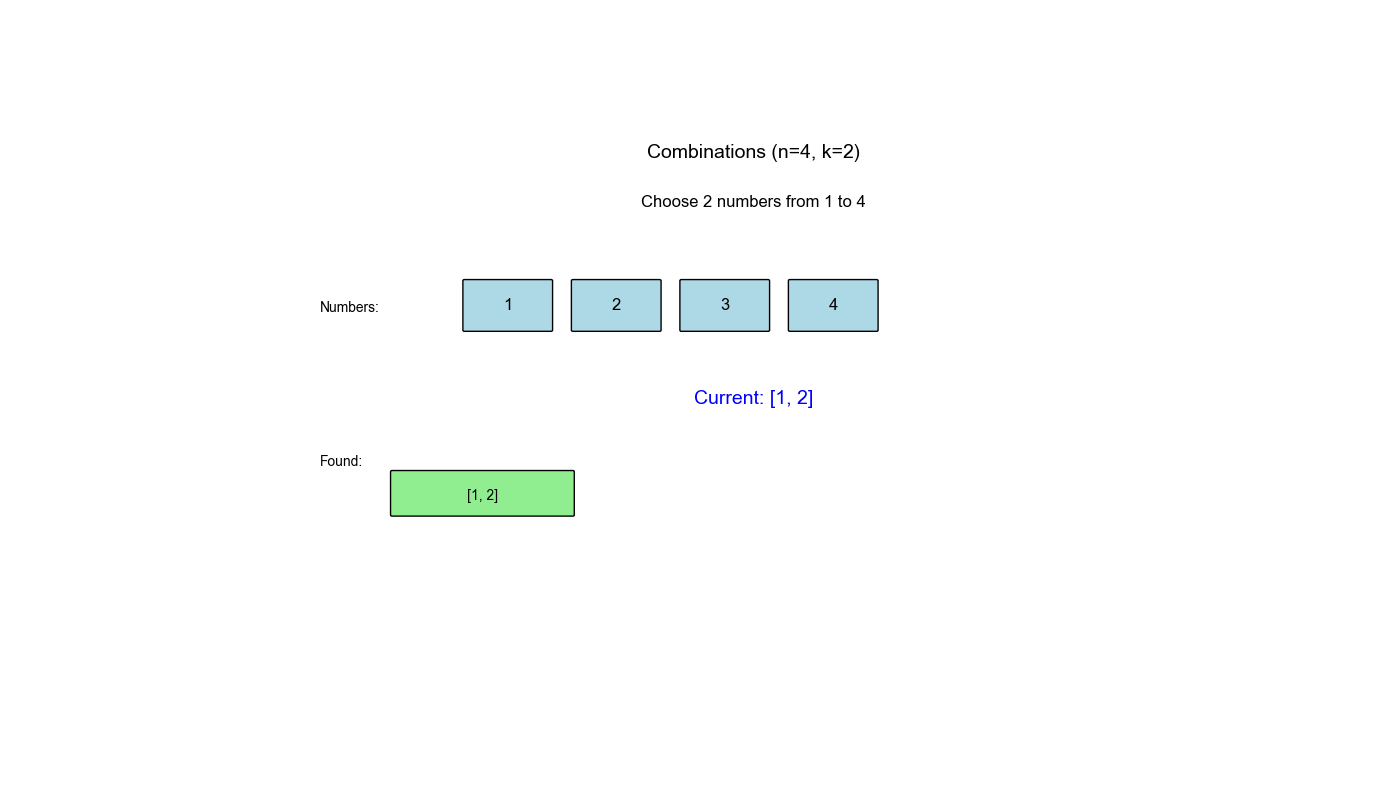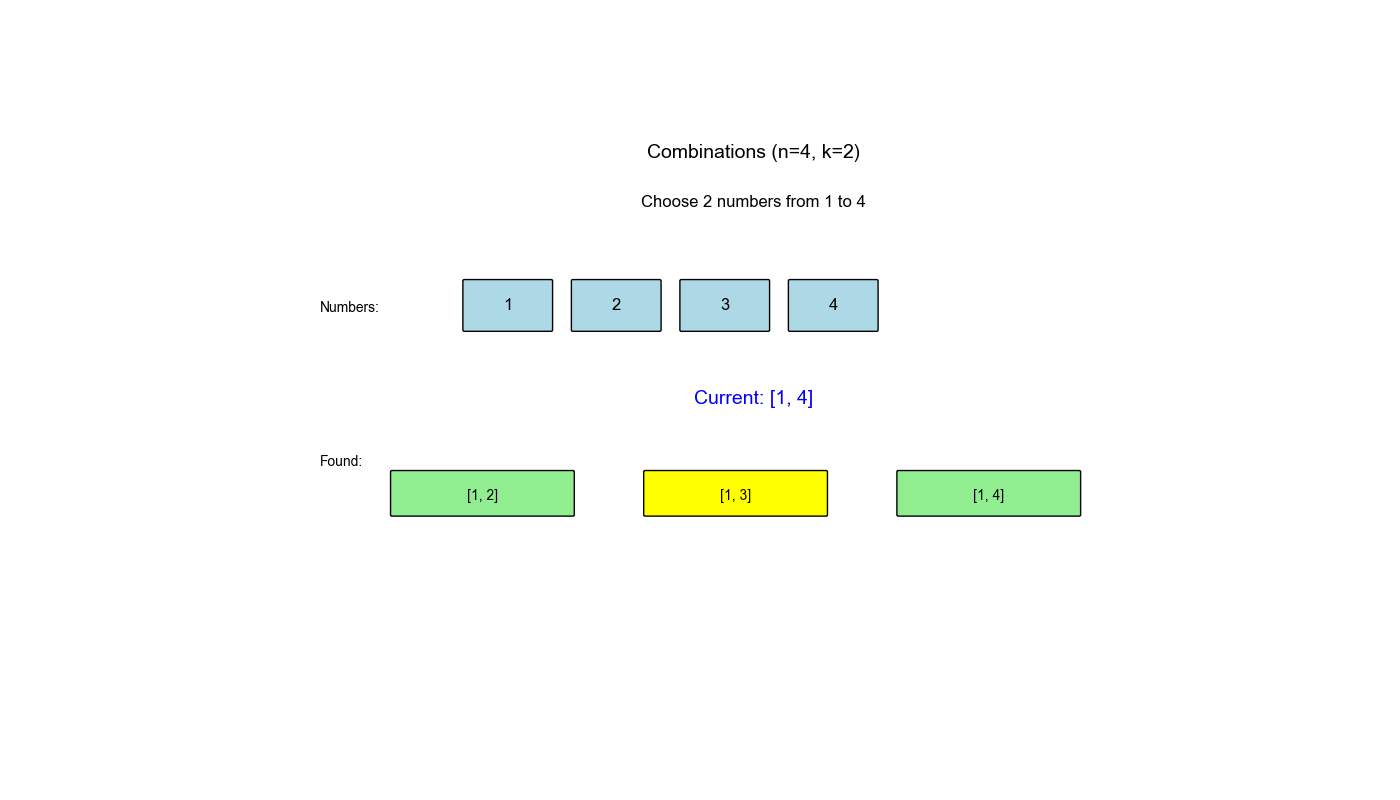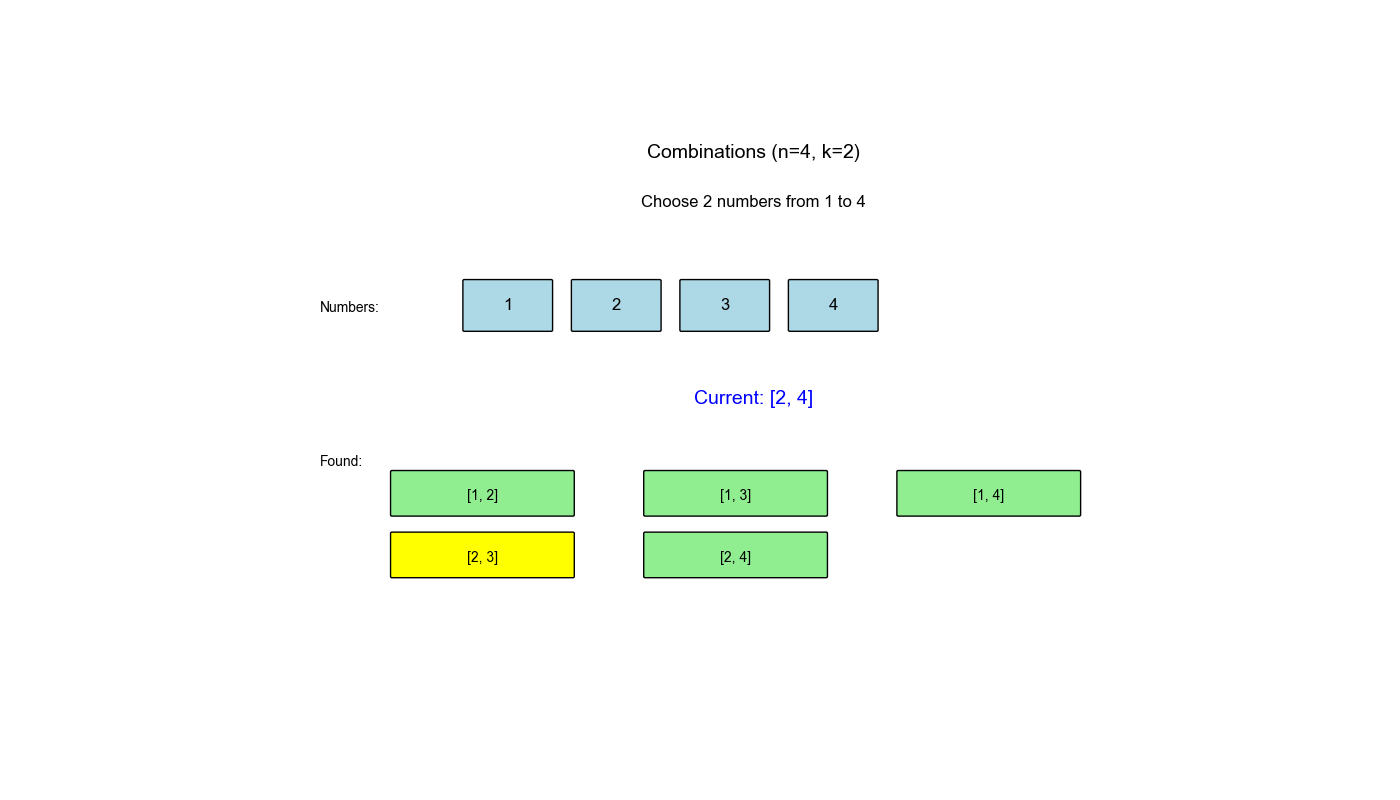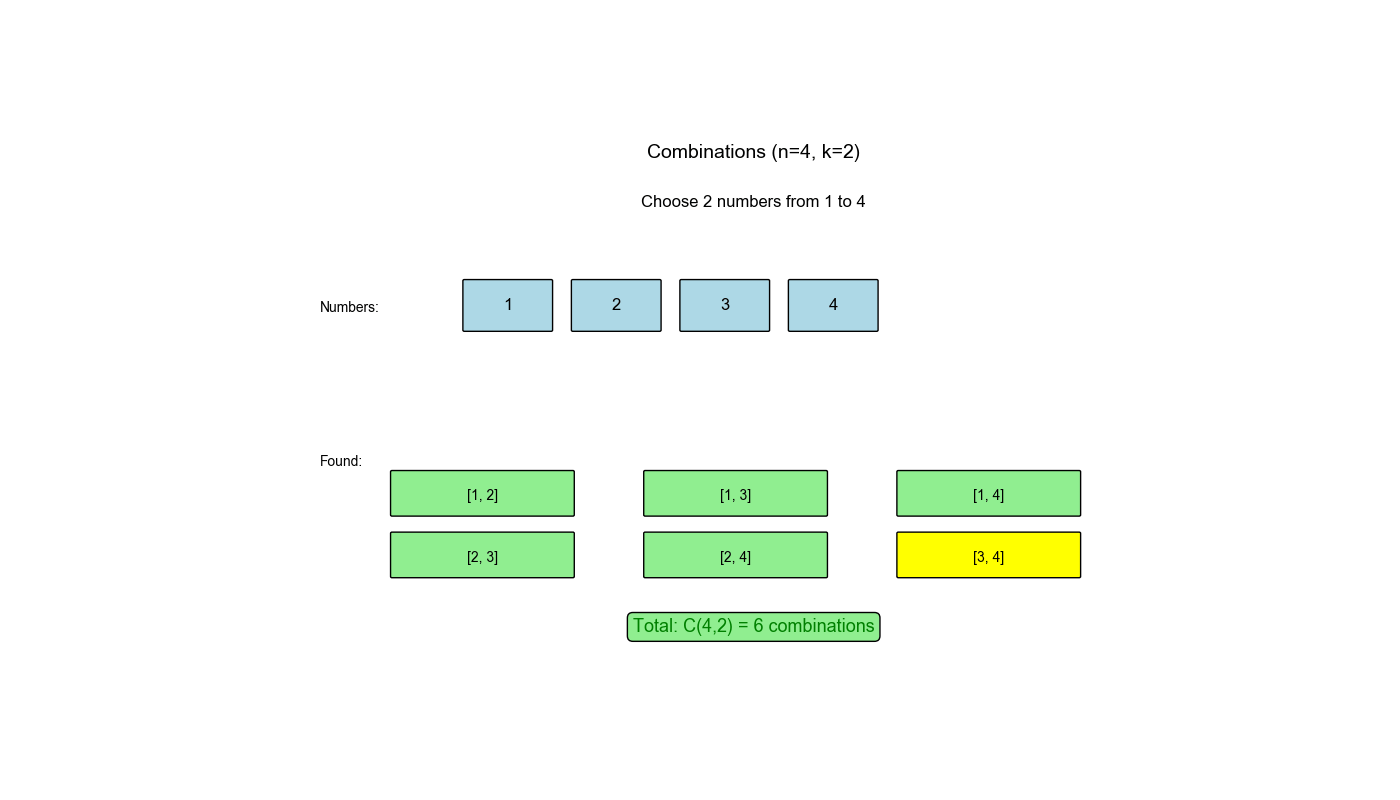
LeetCode 78: 子集

给定一个不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。可以按任意顺序返回解集。

示例：

  • 输入：nums = [1,2,3]
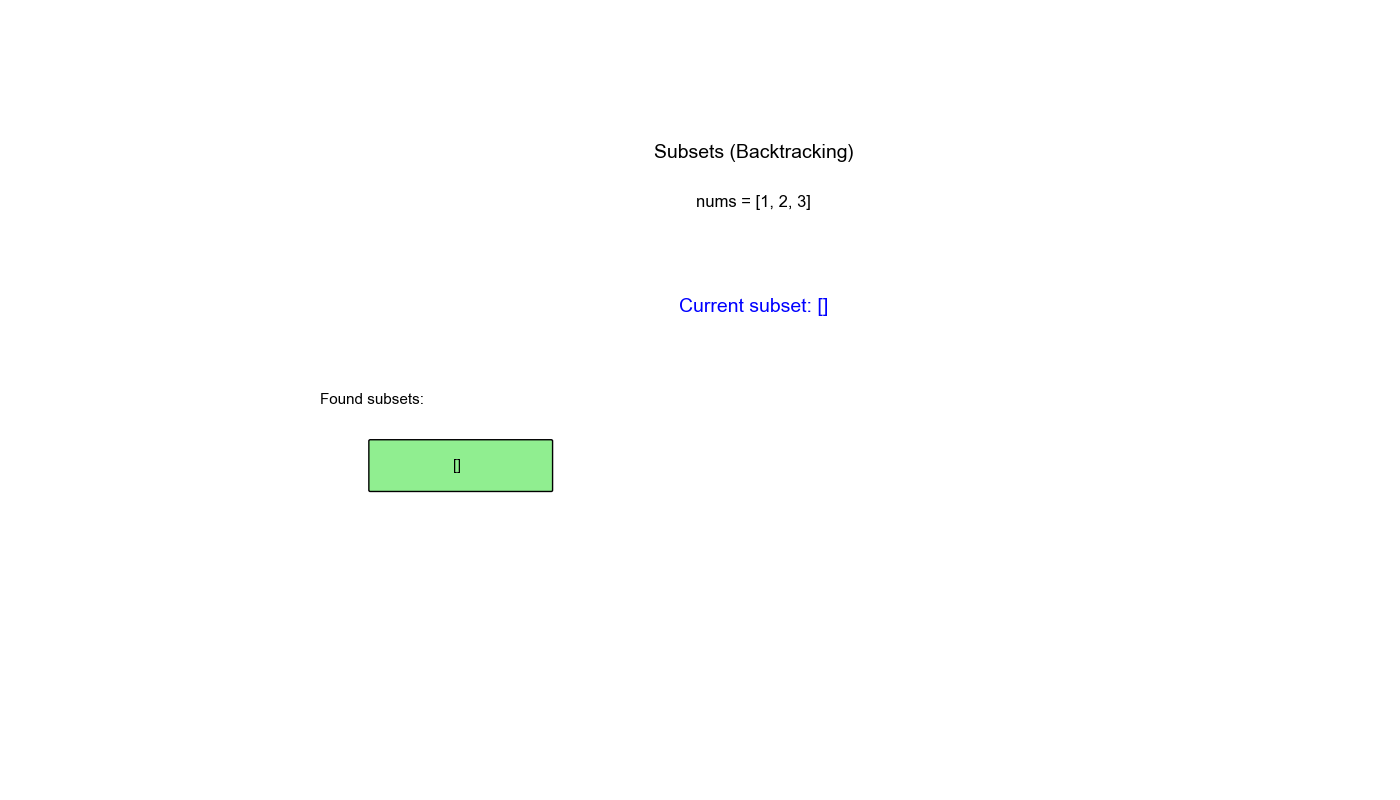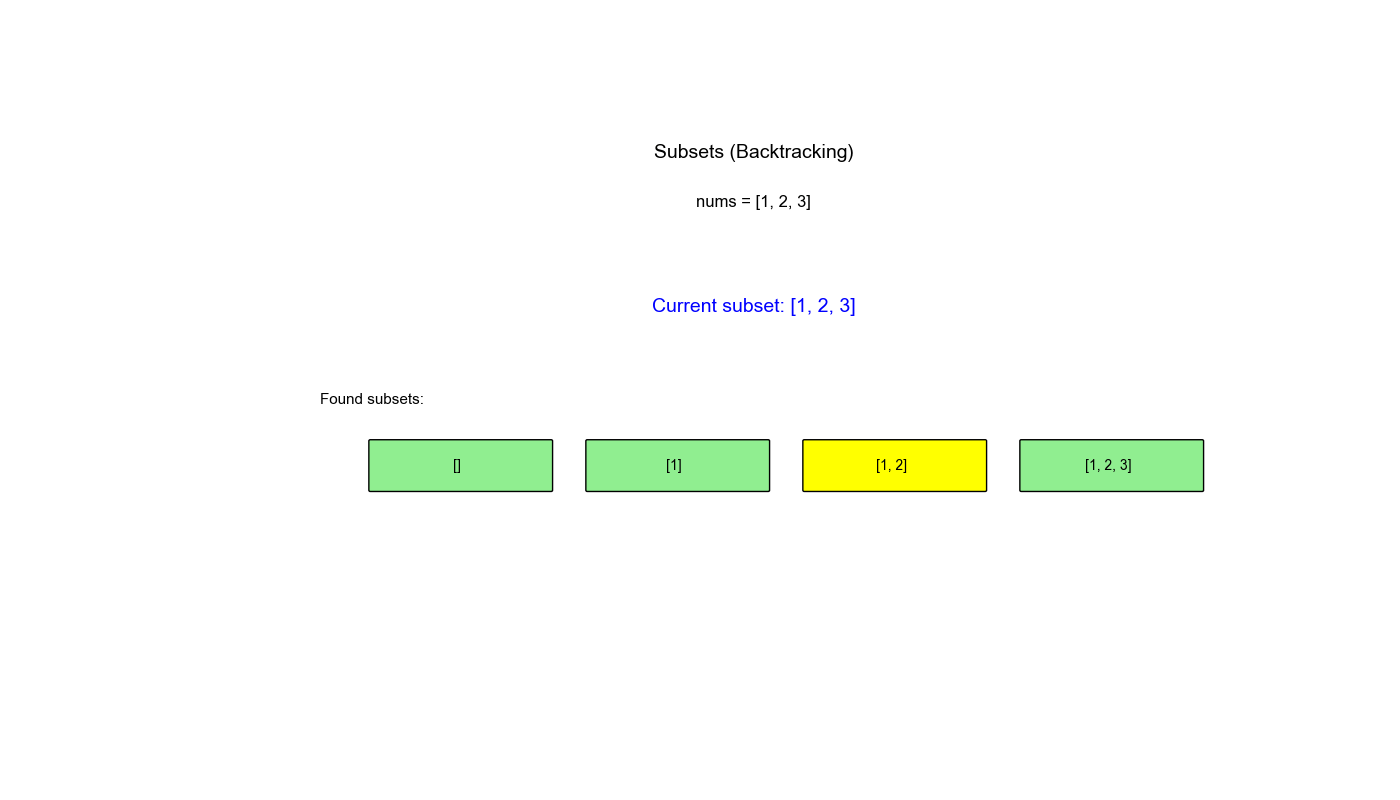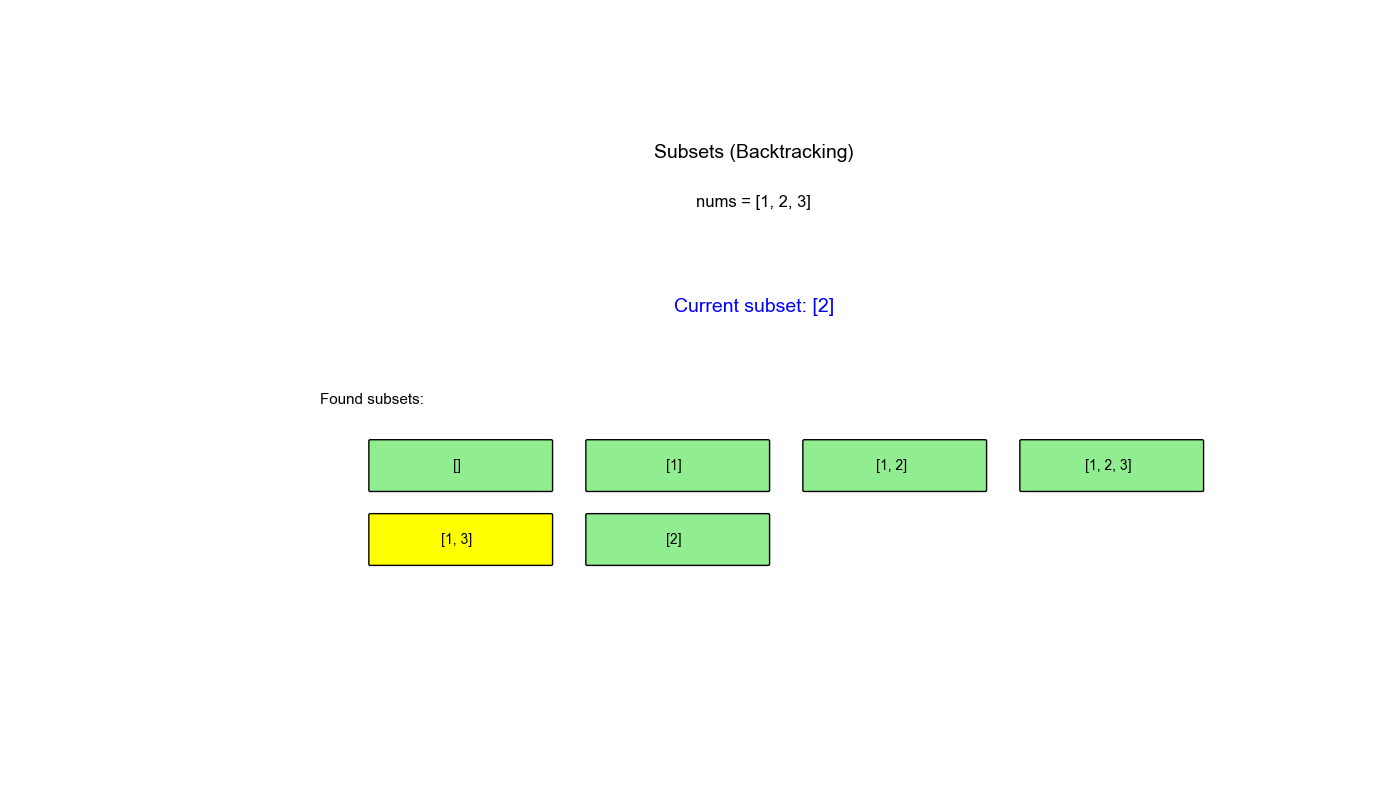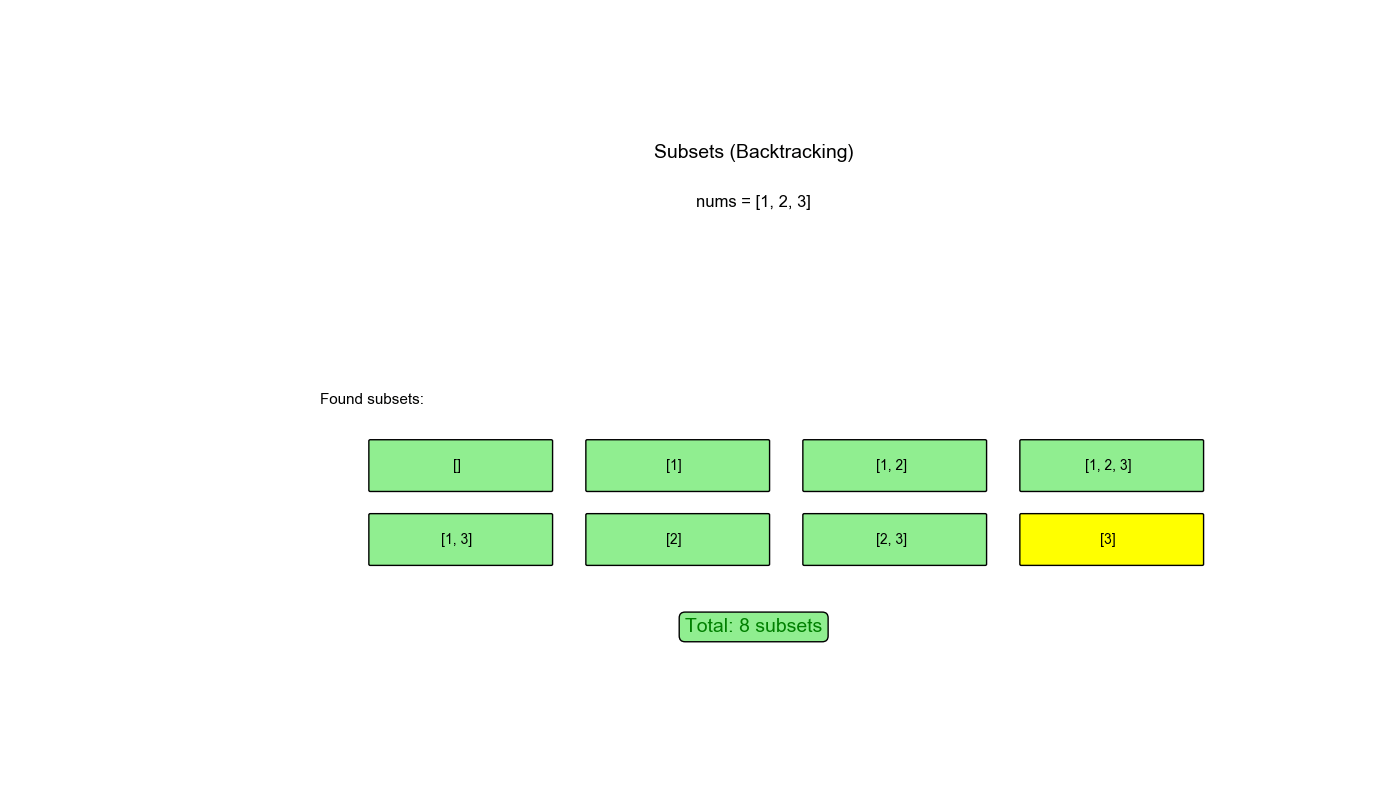
  • 输出：[[], [1], [2], [3], [1,2], [1,3], [2,3], [1,2,3]]

约束条件：

  • nums 中的所有元素互不相同

问题分析

子集问题要求生成数组的所有子集（幂集）。对于 个元素，共有 个子集（包括空集）。

核心特点：

  1. 每个状态都是一个解：与全排列、组合问题不同，子集问题不需要等到满足某个条件才保存结果，而是在每个递归状态都保存当前路径
  2. 如何避免重复：通过 start 参数限制选择范围，确保子集按数组顺序生成
  3. 两种理解方式：
    • 方式一：对每个元素，有两个选择（选或不选）
    • 方式二：逐步添加元素到集合中

解题思路

回溯三要素分析：

  • 选择：是否将当前元素加入子集（从 start 位置开始）
  • 约束：只能从当前位置及之后选择（避免重复）
  • 目标：每个状态都是一个有效子集（无需特定终止条件）

算法流程：

  1. 定义回溯函数 backtrack(start)：
    • 保存当前路径（每个状态都是一个解）
    • 从 start 开始遍历剩余元素
    • 加入当前元素，递归，回溯
  2. 与组合问题的区别：
    • 组合问题：只在满足条件时保存结果
    • 子集问题：每个递归调用开始时都保存结果

复杂度分析

时间复杂度： - 共有 个子集 - 每个子集需要 时间复制到结果中 - 总时间复杂度： 空间复杂度： - 递归栈深度：（最多 层递归） - path 数组： - 结果数组：（输出空间，不计入复杂度）

复杂度证明：

对于 个元素，每个元素有"选"或"不选"两种状态，因此共有 种组合，即 个子集。

方法一：回溯法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from typing import List

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        """
        生成数组的所有子集（幂集）
        
        算法步骤：
        1. 定义回溯函数 backtrack(start)：
           a. 保存当前路径（每个状态都是一个解）
           b. 从 start 开始遍历剩余元素
           c. 做选择：加入路径
           d. 递归： backtrack(i + 1)
           e. 撤销选择：移除路径
        
        边界条件：
        - 空数组：返回 [[]]
        - 单元素：返回 [[], [元素]]
        
        优化技巧：
        - 使用 start 参数避免重复子集
        - 每次递归开始时保存当前状态
        
        变量含义：
        - result: 存储所有子集的结果列表
        - path: 当前正在构建的子集路径
        - start: 当前可以选择的位置起始索引
        """
        result = []
        path = []
        
        def backtrack(start):
            # 每个状态都是一个解（包括空集）
            result.append(path[:])
            
            # 从 start 开始选择，避免重复
            for i in range(start, len(nums)):
                # 做选择
                path.append(nums[i])
                
                # 递归：从 i+1 开始（每个元素只能选一次）
                backtrack(i + 1)
                
                # 撤销选择（回溯）
                path.pop()
        
        backtrack(0)
        return result

算法原理：

为什么每个状态都要保存：

子集问题的本质是"选或不选"的组合。当我们遍历到某个位置时，之前的选择已经形成了一个有效子集。例如：

1
2
3
4
5
6
7
8
9
10
11
12
nums = [1,2,3]
初始： path = [] → 保存 []
选择 1： path = [1] → 保存 [1]
  选择 2： path = [1,2] → 保存 [1,2]
    选择 3： path = [1,2,3] → 保存 [1,2,3]
    回溯： path = [1,2]
  回溯： path = [1]
  选择 3： path = [1,3] → 保存 [1,3]
  回溯： path = [1]
回溯： path = []
选择 2： path = [2] → 保存 [2]
  ...

执行过程示例（nums = [1,2,3]）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
backtrack(0): path=[] → 保存 []
  选择 1: path=[1] → 保存 [1]
    backtrack(1): path=[1]
      选择 2: path=[1,2] → 保存 [1,2]
        backtrack(2): path=[1,2]
          选择 3: path=[1,2,3] → 保存 [1,2,3]
          回溯: path=[1,2]
      回溯: path=[1]
      选择 3: path=[1,3] → 保存 [1,3]
      回溯: path=[1]
  回溯: path=[]
  选择 2: path=[2] → 保存 [2]
    选择 3: path=[2,3] → 保存 [2,3]
  回溯: path=[]
  选择 3: path=[3] → 保存 [3]
结果: [[], [1], [1,2], [1,2,3], [1,3], [2], [2,3], [3]]

常见错误：

错误一：只在叶子节点保存结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# ❌ 错误
def backtrack(start):
    if start == len(nums):  # 只在叶子节点保存
        result.append(path[:])
        return
    for i in range(start, len(nums)):
        path.append(nums[i])
        backtrack(i + 1)
        path.pop()
# 会漏掉很多子集

# ✅ 正确
def backtrack(start):
    result.append(path[:])  # 每个状态都保存
    for i in range(start, len(nums)):
        path.append(nums[i])
        backtrack(i + 1)
        path.pop()

方法二：位运算

对于小规模问题，也可以用位运算：

1
2
3
4
5
6
7
8
9
10
11
def subsets(nums):
    result = []
    n = len(nums)
    # 每个数字对应一个 bit，共 2^n 种组合
    for i in range(1 << n):
        subset = []
        for j in range(n):
            if i & (1 << j):
                subset.append(nums[j])
        result.append(subset)
    return result

时间复杂度：，共有 个子集，每个子集需要 时间复制。

空间复杂度：，递归栈深度为 。

子集问题的另一种理解

子集问题可以理解为：对于每个元素，我们有两个选择：包含或不包含。因此，对于 个元素，共有 种选择方式，对应 个子集。

这种理解方式对应了另一种实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def subsets(nums):
    result = []
    path = []
    
    def backtrack(index):
        # 终止条件：处理完所有元素
        if index == len(nums):
            result.append(path[:])
            return
        
        # 选择 1：不包含当前元素
        backtrack(index + 1)
        
        # 选择 2：包含当前元素
        path.append(nums[index])
        backtrack(index + 1)
        path.pop()
    
    backtrack(0)
    return result

这种实现方式更直观地体现了"每个元素有两个选择"的思想，但两种实现的时间复杂度相同。

子集 II（包含重复元素）

如果数组包含重复元素，需要去重：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def subsetsWithDup(nums):
    result = []
    path = []
    nums.sort()  # 排序以便去重
    
    def backtrack(start):
        result.append(path[:])
        
        for i in range(start, len(nums)):
            # 剪枝：跳过重复元素
            if i > start and nums[i] == nums[i-1]:
                continue
            
            path.append(nums[i])
            backtrack(i + 1)
            path.pop()
    
    backtrack(0)
    return result

LeetCode 51: N 皇后

皇后问题研究的是如何将 个皇后放置在 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n，返回所有不同的 皇后问题的解决方案。

皇后攻击规则：皇后可以攻击与之处在同一行、同一列或同一斜线上的棋子。

示例：

  • 输入：n = 4
  • 输出： 
    1
    2
    [[".Q..","...Q","Q...","..Q."],
     ["..Q.","Q...","...Q",".Q.."]]

约束条件：

问题分析

N 皇后问题是经典的约束满足问题（ CSP），要求在 棋盘上放置 个皇后，使得任意两个皇后不能互相攻击。

核心挑战：

  1. 多重约束：每个皇后不能与其他皇后在同一行、同一列或同一对角线上
  2. 对角线判断：如何高效地判断两个位置是否在同一对角线上
  3. 状态恢复：需要记录和恢复列、对角线的占用状态

关键洞察：

  • 行约束：逐行放置皇后，每行只放一个，自动满足行约束
  • 列约束：使用集合记录已占用的列
  • 对角线约束：
    • 主对角线（左上到右下）：同一对角线上的格子满足 row - col = 常数
    • 副对角线（右上到左下）：同一对角线上的格子满足 row + col = 常数

解题思路

回溯三要素分析：

  • 选择：在当前行选择哪一列放置皇后（ 0 到 n-1）
  • 约束：
    • 该列未被占用
    • 主对角线未被占用（row - col 不在已占用集合中）
    • 副对角线未被占用（row + col 不在已占用集合中）
  • 目标：成功放置 个皇后（row == n）

算法流程：

  1. 使用三个集合分别记录已占用的列、主对角线、副对角线
  2. 定义回溯函数 backtrack(row)：
    • 终止条件：row == n，保存当前棋盘
    • 遍历当前行的所有列
    • 检查约束：列、主对角线、副对角线都未占用
    • 做选择：放置皇后，更新集合
    • 递归处理下一行
    • 撤销选择：移除皇后，恢复集合

复杂度分析

时间复杂度： - 第一行有 种选择 - 第二行最多 种选择（至少有一列被占用） - 第三行最多 种选择 - ... - 总搜索节点数约为 - 实际由于对角线约束，搜索空间更小

空间复杂度： - 递归栈深度： - 棋盘： - 三个集合： 复杂度证明：

虽然理论上第一行有 个选择，第二行有 个选择，总共 种可能，但由于列约束和对角线约束，实际搜索空间远小于 。通过剪枝，复杂度降低到 。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
from typing import List

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        """
        N 皇后问题：在 n × n 棋盘上放置 n 个皇后，使其不互相攻击
        
        算法步骤：
        1. 初始化棋盘和三个集合（列、主对角线、副对角线）
        2. 定义回溯函数 backtrack(row)：
           a. 终止条件： row == n，保存棋盘
           b. 遍历当前行的每一列
           c. 约束检查：列、主对角线、副对角线都未占用
           d. 做选择：放置皇后，更新集合
           e. 递归： backtrack(row + 1)
           f. 撤销选择：移除皇后，恢复集合
        
        边界条件：
        - n=1：返回 [["Q"]]
        - n=2, n=3：无解，返回 []
        
        优化技巧：
        - 使用集合 O(1)判断约束，比遍历检查快
        - 逐行放置，自动满足行约束
        - 对角线公式：主对角线 row-col，副对角线 row+col
        
        变量含义：
        - result: 存储所有有效解的列表
        - board: n × n 棋盘，'Q'表示皇后，'.'表示空格
        - cols: 已占用的列集合
        - diag1: 已占用的主对角线集合（ row - col）
        - diag2: 已占用的副对角线集合（ row + col）
        """
        result = []
        board = [['.'] * n for _ in range(n)]
        cols = set()  # 已占用的列
        diag1 = set()  # 主对角线： row - col
        diag2 = set()  # 副对角线： row + col
        
        def backtrack(row):
            # 终止条件：成功放置 n 个皇后
            if row == n:
                # 转换为题目要求的格式
                result.append([''.join(row) for row in board])
                return
            
            # 尝试在当前行的每一列放置皇后
            for col in range(n):
                # 约束检查
                if col in cols or (row - col) in diag1 or (row + col) in diag2:
                    continue  # 该位置不满足约束，跳过
                
                # 做选择
                board[row][col] = 'Q'
                cols.add(col)
                diag1.add(row - col)
                diag2.add(row + col)
                
                # 递归：处理下一行
                backtrack(row + 1)
                
                # 撤销选择（回溯）
                board[row][col] = '.'
                cols.remove(col)
                diag1.remove(row - col)
                diag2.remove(row + col)
        
        backtrack(0)
        return result

算法原理：

为什么对角线公式有效：

对于棋盘上的位置 ： - 主对角线：从左上到右下，同一对角线上的格子满足 $ r - c = k（常数）例如：(0,0)$, , 都满足 - 例如：, , 都满足 - 副对角线：从右上到左下，同一对角线上的格子满足 $ r + c = k（常数）例如：(0,2)$, , 都满足 - 例如：, , , 都满足 执行过程示例（）：

1
2
3
4
5
6
row=0: 尝试 col=0, 放置皇后， cols={0}, diag1={0}, diag2={0}
  row=1: 尝试 col=0, 冲突（列）
         尝试 col=1, 冲突（主对角线： 1-1=0）
         尝试 col=2, 可行，放置皇后
    row=2: 尝试各列...
    ...

常见错误：

错误一：对角线判断错误

1
2
3
4
5
6
7
# ❌ 错误：直接用 row 和 col 判断
if board[i][col] == 'Q':  # 需要遍历整个列和对角线， O(n)
    continue

# ✅ 正确：使用集合和公式， O(1)
if col in cols or (row - col) in diag1 or (row + col) in diag2:
    continue

错误二：忘记恢复所有状态

1
2
3
4
5
6
7
8
9
10
# ❌ 错误：只恢复部分状态
board[row][col] = '.'
cols.remove(col)
# 忘记： diag1.remove(row - col) 和 diag2.remove(row + col)

# ✅ 正确：恢复所有状态
board[row][col] = '.'
cols.remove(col)
diag1.remove(row - col)
diag2.remove(row + col)

N 皇后问题的优化技巧

优化一：使用位运算

对于小规模的 N 皇后问题，可以使用位运算来加速约束检查：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def solveNQueens(n):
    result = []
    board = [['.'] * n for _ in range(n)]
    
    def backtrack(row, cols, diag1, diag2):
        if row == n:
            result.append([''.join(row) for row in board])
            return
        
        # 计算可用的列
        available = ((1 << n) - 1) & (~(cols | diag1 | diag2))
        
        while available:
            # 获取最低位的 1
            col = available & -available
            col_index = bin(col - 1).count('1')
            
            board[row][col_index] = 'Q'
            backtrack(row + 1, 
                     cols | col, 
                     (diag1 | col) << 1, 
                     (diag2 | col) >> 1)
            board[row][col_index] = '.'
            
            # 移除最低位的 1
            available &= available - 1
    
    backtrack(0, 0, 0, 0)
    return result

优化二：只统计解的个数

如果只需要统计解的个数而不需要具体解，可以进一步优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def totalNQueens(n):
    count = 0
    cols = set()
    diag1 = set()
    diag2 = set()
    
    def backtrack(row):
        nonlocal count
        if row == n:
            count += 1
            return
        
        for col in range(n):
            if col in cols or (row - col) in diag1 or (row + col) in diag2:
                continue
            
            cols.add(col)
            diag1.add(row - col)
            diag2.add(row + col)
            backtrack(row + 1)
            cols.remove(col)
            diag1.remove(row - col)
            diag2.remove(row + col)
    
    backtrack(0)
    return count

这种优化避免了构建和保存棋盘状态，只统计解的个数，空间复杂度更低。

LeetCode 22: 括号生成

数字 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。

示例：

  • 输入：n = 3
  • 输出：["((()))", "(()())", "(())()", "()(())", "()()()"]

约束条件：

问题分析

括号生成问题要求生成所有有效的括号序列。对于 对括号，有效序列的数量等于第 个卡特兰数 。

核心挑战：

  1. 如何保证括号有效：任何时候右括号数量不能超过左括号数量
  2. 如何避免无效搜索：通过约束条件提前剪枝
  3. 如何系统地生成所有可能性：使用回溯探索所有选择

关键洞察：

  • 约束 1：左括号数量不能超过
  • 约束 2：右括号数量不能超过左括号数量（否则无法匹配）
  • 终止条件：生成长度为 的序列

解题思路

回溯三要素分析：

  • 选择：当前位置放置左括号 ( 还是右括号 )
  • 约束：
    • 左括号：left < n（左括号数量未达到上限）
    • 右括号：right < left（右括号数量少于左括号）
  • 目标：生成长度为 的有效括号序列（len(path) == 2n）

算法流程：

  1. 定义回溯函数 backtrack(left, right)：
    • left：已使用的左括号数量
    • right：已使用的右括号数量
  2. 终止条件：len(path) == 2n，保存结果
  3. 尝试两种选择：
    • 如果 left < n，可以放置左括号
    • 如果 right < left，可以放置右括号

复杂度分析

时间复杂度： 这是第 个卡特兰数的渐近复杂度。第 个卡特兰数：

$$

C_n = = $$

空间复杂度： - 递归栈深度： - path 数组： 复杂度证明：

括号序列的数量等于卡特兰数 。对于 $ n=3，C_3 = 5；对于 n=4，C_4 = 14$。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from typing import List

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        """
        生成所有有效的 n 对括号组合
        
        算法步骤：
        1. 定义回溯函数 backtrack(left, right)：
           a. 终止条件： len(path) == 2n，保存结果
           b. 选择 1：如果 left < n，放置左括号'('
           c. 选择 2：如果 right < left，放置右括号')'
           d. 每次选择后递归，然后回溯
        
        边界条件：
        - n=1：返回 ["()"]
        - n=0：返回 [""]（根据约束不会发生）
        
        优化技巧：
        - 通过约束条件提前剪枝，避免生成无效序列
        - 只在 right < left 时放置右括号，保证有效性
        
        变量含义：
        - result: 存储所有有效括号序列的列表
        - path: 当前正在构建的括号序列
        - left: 已使用的左括号数量
        - right: 已使用的右括号数量
        """
        result = []
        path = []
        
        def backtrack(left, right):
            # 终止条件：生成长度为 2n 的序列
            if len(path) == 2 * n:
                result.append(''.join(path))
                return
            
            # 选择 1：放置左括号
            if left < n:
                path.append('(')
                backtrack(left + 1, right)
                path.pop()
            
            # 选择 2：放置右括号（需要满足约束）
            if right < left:
                path.append(')')
                backtrack(left, right + 1)
                path.pop()
        
        backtrack(0, 0)
        return result

算法原理：

为什么 right < left 能保证有效：

括号序列有效的充要条件是： 1. 左右括号数量相等 2. 任何前缀中，左括号数量 ≥ 右括号数量

通过在递归过程中维护 right < left，确保了条件 2 始终满足。终止时 left == right == n，满足条件 1 。

卡特兰数的数学背景：

括号生成问题与卡特兰数密切相关。卡特兰数在组合数学中有很多应用：

  • 对括号的有效序列数
  • 个节点的不同二叉搜索树数量
  • 边形的三角剖分数
  • 在 网格中，从左下角到右上角不越过对角线的路径数

执行过程示例（n = 2）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
backtrack(0,0): path=[]
  选择'(': path=['('], left=1, right=0
    选择'(': path=['(',  '('], left=2, right=0
      选择')': path=['(', '(', ')'], left=2, right=1
        选择')': path=['(', '(', ')', ')'] → 保存 "(())"
        回溯: path=['(', '(', ')']
      回溯: path=['(', '(']
    回溯: path=['(']
    选择')': path=['(', ')'], left=1, right=1
      选择'(': path=['(', ')', '('], left=2, right=1
        选择')': path=['(', ')', '(', ')'] → 保存 "()()"
        回溯: path=['(', ')', '(']
      回溯: path=['(', ')']
    回溯: path=['(']
  回溯: path=[]
结果: ["(())", "()()"]

常见错误：

错误一：没有约束检查

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# ❌ 错误：没有检查 left < n 和 right < left
path.append('(')
backtrack(left + 1, right)
path.pop()
path.append(')')
backtrack(left, right + 1)
path.pop()
# 会生成无效序列如 "))(("

# ✅ 正确
if left < n:
    path.append('(')
    backtrack(left + 1, right)
    path.pop()
if right < left:
    path.append(')')
    backtrack(left, right + 1)
    path.pop()

括号生成问题的数学背景

括号生成问题与卡特兰数（ Catalan Number）密切相关。第 个卡特兰数表示 对括号可以组成的不同有效括号序列的数量。

卡特兰数在组合数学中有很多应用：

  • 对括号的有效序列数
  • 个节点的不同二叉搜索树数量
  • 边形的三角剖分数
  • 在 网格中，从左下角到右上角不越过对角线的路径数

括号生成问题的其他解法

方法一：动态规划

1
2
3
4
5
6
7
8
9
10
11
def generateParenthesis(n):
    if n == 0:
        return ['']
    
    result = []
    for i in range(n):
        for left in generateParenthesis(i):
            for right in generateParenthesis(n - 1 - i):
                result.append('(' + left + ')' + right)
    
    return result

这种方法的思路是：第一个括号内包含 对括号，第一个括号外包含 对括号。

方法二：迭代生成

1
2
3
4
5
6
7
8
9
10
11
12
13
def generateParenthesis(n):
    result = ['']
    for _ in range(2 * n):
        new_result = []
        for s in result:
            left_count = s.count('(')
            right_count = s.count(')')
            if left_count < n:
                new_result.append(s + '(')
            if right_count < left_count:
                new_result.append(s + ')')
        result = new_result
    return result

这种方法逐字符生成，每次添加一个左括号或右括号，保证始终满足约束条件。

剪枝优化技巧

剪枝是回溯算法优化的重要手段，通过提前排除不可能的分支，大幅减少搜索空间。

1. 约束剪枝

在进入递归前检查约束条件，不满足则跳过：

1
2
3
4
for choice in choices:
    if 不满足约束条件:  # 剪枝
        continue
    # 做选择并递归

示例：组合总和问题中，如果剩余值小于 0，直接返回。

2. 重复剪枝

对于包含重复元素的问题，通过排序和跳过相同元素避免重复：

1
2
3
4
nums.sort()
for i in range(start, len(nums)):
    if i > start and nums[i] == nums[i-1]:
        continue  # 跳过重复元素

3. 可行性剪枝

提前判断当前分支是否可能产生解：

1
2
3
# 如果剩余元素不足以构成解，剪枝
if len(path) + (n - i) < target_length:
    return

4. 上下界剪枝

在搜索过程中维护上下界，提前排除不可能的范围：

1
2
3
4
5
6
# 当前和 + 剩余最大和 < target，剪枝
if current_sum + max_remaining_sum < target:
    return
# 当前和 + 剩余最小和 > target，剪枝
if current_sum + min_remaining_sum > target:
    return

5. 对称性剪枝

利用问题的对称性减少搜索：

1
2
3
# 例如：全排列中，如果 nums[i] == nums[j]，且 i < j
# 那么选择 nums[i] 和 nums[j] 的结果是对称的
# 可以只选择其中一个

时间复杂度分析

回溯算法的时间复杂度分析通常比较复杂，因为需要分析所有可能的搜索路径。

一般分析方法

  1. 确定搜索树的大小：有多少个节点？
  2. 确定每个节点的处理时间：生成子节点需要多少时间？
  3. 总时间复杂度 = 节点数 × 每个节点的处理时间

常见复杂度

  • 全排列： - 共有 个叶子节点（排列）
    • 每个排列需要 时间复制
  • 子集： - 共有 个子集
    • 每个子集需要 时间复制
  • 组合： - 共有 个组合
    • 每个组合需要 时间复制
  • N 皇后： - 第一行 种选择，第二行最多 种，以此类推

优化后的复杂度

剪枝可以大幅减少实际搜索的节点数，但最坏情况复杂度通常不变。平均情况下，剪枝可能将复杂度降低一个数量级。

更多经典问题

单词搜索

问题描述：给定一个二维网格和一个单词，找出该单词是否存在于网格中。单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中"相邻"单元格是那些水平相邻或垂直相邻的单元格。

思路：从网格的每个位置开始，使用回溯算法搜索单词。需要标记已访问的单元格，回溯时恢复状态。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def exist(board, word):
    m, n = len(board), len(board[0])
    directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
    
    def backtrack(row, col, index):
        if index == len(word):
            return True
        
        if row < 0 or row >= m or col < 0 or col >= n:
            return False
        
        if board[row][col] != word[index]:
            return False
        
        # 标记为已访问
        temp = board[row][col]
        board[row][col] = '#'
        
        # 尝试四个方向
        for dr, dc in directions:
            if backtrack(row + dr, col + dc, index + 1):
                return True
        
        # 回溯：恢复状态
        board[row][col] = temp
        return False
    
    for i in range(m):
        for j in range(n):
            if backtrack(i, j, 0):
                return True
    
    return False

数独求解

问题描述：编写一个程序，通过已填充的空格来解决数独问题。数独的解法需遵循规则：数字 1-9 在每一行、每一列和每一个 3x3 宫格内只能出现一次。

思路：使用回溯算法，逐个填充空格。对于每个空格，尝试 1-9 的所有可能值，检查是否满足约束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def solveSudoku(board):
    def isValid(row, col, num):
        # 检查行
        for j in range(9):
            if board[row][j] == num:
                return False
        
        # 检查列
        for i in range(9):
            if board[i][col] == num:
                return False
        
        # 检查 3x3 宫格
        start_row, start_col = (row // 3) * 3, (col // 3) * 3
        for i in range(start_row, start_row + 3):
            for j in range(start_col, start_col + 3):
                if board[i][j] == num:
                    return False
        
        return True
    
    def backtrack():
        for i in range(9):
            for j in range(9):
                if board[i][j] == '.':
                    for num in '123456789':
                        if isValid(i, j, num):
                            board[i][j] = num
                            if backtrack():
                                return True
                            board[i][j] = '.'
                    return False
        return True
    
    backtrack()

复原 IP 地址

问题描述：给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

思路：使用回溯算法，将字符串分成四段，每段是 0-255 之间的数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def restoreIpAddresses(s):
    result = []
    path = []
    
    def backtrack(start):
        # 终止条件：分成四段且用完所有字符
        if len(path) == 4:
            if start == len(s):
                result.append('.'.join(path))
            return
        
        # 每段最多 3 位数字
        for end in range(start, min(start + 3, len(s))):
            segment = s[start:end + 1]
            
            # 约束检查
            if len(segment) > 1 and segment[0] == '0':  # 不能有前导 0
                continue
            if int(segment) > 255:
                continue
            
            path.append(segment)
            backtrack(end + 1)
            path.pop()
    
    backtrack(0)
    return result

常见陷阱与注意事项

1. 结果保存时未复制

1
2
3
4
5
# ❌ 错误
result.append(path)  # path 是引用，后续修改会影响已保存的结果

# ✅ 正确
result.append(path[:])  # 创建副本

2. 状态恢复不完整

1
2
3
4
5
6
7
# ❌ 错误：忘记恢复 used 数组
path.pop()
# used[i] = False  # 遗漏！

# ✅ 正确
path.pop()
used[i] = False

3. 剪枝条件错误

1
2
3
4
5
6
7
# ❌ 错误：去重剪枝条件写反
if i > 0 and nums[i] == nums[i-1] and used[i-1]:
    continue  # 应该是 not used[i-1]

# ✅ 正确
if i > 0 and nums[i] == nums[i-1] and not used[i-1]:
    continue

4. 选择列表更新错误

1
2
3
4
5
# ❌ 错误：在组合问题中从 0 开始选择，导致重复
for i in range(len(nums)):  # 应该从 start 开始

# ✅ 正确
for i in range(start, len(nums)):

5. 终止条件遗漏

1
2
3
4
5
6
7
8
9
# ❌ 错误：忘记检查边界条件
if len(path) == len(nums):
    result.append(path[:])
    # return  # 遗漏！

# ✅ 正确
if len(path) == len(nums):
    result.append(path[:])
    return

回溯算法的迭代实现

虽然回溯算法通常用递归实现，但也可以使用迭代方式。迭代实现使用显式栈来模拟递归调用。

全排列的迭代实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def permute_iterative(nums):
    result = []
    stack = [([], [False] * len(nums))]  # (path, used)
    
    while stack:
        path, used = stack.pop()
        
        if len(path) == len(nums):
            result.append(path)
            continue
        
        for i in range(len(nums)):
            if not used[i]:
                new_path = path + [nums[i]]
                new_used = used[:]
                new_used[i] = True
                stack.append((new_path, new_used))
    
    return result

子集的迭代实现

1
2
3
4
5
6
7
8
9
10
11
def subsets_iterative(nums):
    result = [[]]
    
    for num in nums:
        # 对于已有的每个子集，添加当前数字形成新子集
        new_subsets = []
        for subset in result:
            new_subsets.append(subset + [num])
        result.extend(new_subsets)
    
    return result

迭代实现的优势：

  • 避免栈溢出问题
  • 可以更好地控制搜索顺序
  • 在某些情况下可能更高效

迭代实现的劣势：

  • 代码通常更复杂
  • 状态管理更困难
  • 对于复杂问题，递归实现更直观

回溯算法与其他算法的关系

回溯 vs 动态规划

回溯算法和动态规划都用于解决优化问题，但适用场景不同：

  • 回溯算法：需要找出所有解，时间复杂度通常是指数级
  • 动态规划：需要找出最优解，通过记忆化将时间复杂度降低到多项式级

有些问题既可以用回溯也可以用动态规划，选择取决于需求：

  • 如果需要所有解：用回溯
  • 如果只需要最优解：用动态规划

回溯 vs 贪心算法

回溯算法和贪心算法都通过做选择来解决问题：

  • 回溯算法：系统地尝试所有选择，如果当前选择不可行就回溯
  • 贪心算法：每次选择当前看起来最优的选择，不回溯

贪心算法通常更快，但只能保证局部最优，不一定得到全局最优解。回溯算法虽然慢，但可以保证找到所有解或全局最优解。

回溯 vs 分支限界

回溯算法和分支限界（ Branch and Bound）都是搜索算法：

  • 回溯算法：深度优先搜索，找到解后继续搜索其他解
  • 分支限界：广度优先或最佳优先搜索，使用界限函数剪枝

分支限界通常用于优化问题，通过界限函数提前排除不可能产生最优解的分支。

实战技巧总结

  1. 先画搜索树：在编码前画出问题的搜索树，理解选择、约束和目标。

  2. 使用模板：掌握回溯模板，大部分问题都可以套用。

  3. 注意去重：对于包含重复元素的问题，排序 + 剪枝是常用方法。

  4. 合理剪枝：根据问题特点设计剪枝策略，可以大幅提升效率。

  5. 状态管理：使用合适的数据结构（集合、数组）管理状态，提高约束检查效率。

  6. 边界处理：仔细处理边界条件，避免数组越界或无限递归。

  7. 调试技巧：在关键位置打印 path 和选择列表，理解搜索过程。

❓ Q&A: 回溯算法常见问题

Q1: 回溯算法和 DFS 有什么区别？

A: 回溯算法是 DFS 的一种应用形式。 DFS 专注于遍历所有节点，而回溯算法在 DFS 的基础上增加了状态恢复机制。回溯算法在递归返回时会撤销之前的选择，恢复到上一个状态，以便尝试其他可能性。没有状态恢复的 DFS 无法解决需要探索所有可能组合的问题。

Q2: 为什么回溯算法中要用 path[:] 而不是 path？

A: path 是一个列表引用，如果直接 append(path)，保存的是同一个引用。当后续修改 path 时（如 path.pop()），已保存的结果也会被修改。path[:] 创建了 path 的浅拷贝，保存的是独立的副本，后续修改不会影响已保存的结果。

Q3: 如何判断一个问题是否适合用回溯算法？

A: 适合用回溯算法的问题通常具有以下特征： 1. 需要找出所有可能的解（而不是单一最优解） 2. 解可以表示为一系列选择 3. 选择之间有约束关系 4. 可以通过试错的方式探索所有可能性

典型问题包括：排列、组合、子集、 N 皇后、数独、括号生成等。

Q4: 回溯算法的时间复杂度如何分析？

A: 回溯算法的时间复杂度通常是指数级的。分析方法： 1. 确定搜索树的节点数（通常是 或 ） 2. 确定每个节点的处理时间（通常是 或 ） 3. 总复杂度 = 节点数 × 每个节点的处理时间

例如，全排列问题有 个叶子节点，每个节点需要 时间，总复杂度为 。

Q5: 如何优化回溯算法的性能？

A: 主要优化方法： 1. 剪枝：提前排除不可能的分支 2. 排序：对输入排序，便于去重和剪枝 3. 记忆化：对于重叠子问题，使用记忆化避免重复计算 4. 约束传播：利用约束关系提前缩小搜索空间 5. 启发式搜索：优先探索更可能产生解的分支

Q6: 去重剪枝中 used[i-1] 的判断逻辑是什么？

A: 在包含重复元素的排列/组合问题中，排序后相同元素会相邻。去重策略是：如果当前元素与前一个元素相同，且前一个元素未被使用，则跳过当前元素。

这是因为：如果前一个相同元素未被使用，说明我们在同一层已经尝试过选择它，当前选择会产生重复结果。如果前一个元素已被使用，说明我们在上一层选择了它，当前选择是合法的（因为位置不同）。

Q7: 组合问题中为什么要从 start 开始选择？

A: 组合问题要求结果中元素的顺序不重要（[1,2] 和 [2,1] 是同一个组合）。如果从 0 开始选择，会产生重复。例如选择 2 后再选择 1，和选择 1 后再选择 2 是重复的。

从 start 开始选择保证了我们总是按照数组的顺序选择元素，避免了重复组合。每次递归时，start 递增，确保不会选择之前的元素。

Q8: 回溯算法会栈溢出吗？

A: 可能会。回溯算法使用递归实现，递归深度等于问题的规模。对于大规模问题（如 的全排列），递归深度可能很大，导致栈溢出。

解决方法： 1. 迭代实现：使用显式栈模拟递归 2. 限制深度：对于超大规模问题，考虑其他算法 3. 尾递归优化：某些语言支持尾递归优化（但 Python 不支持）

Q9: 如何将回溯算法改为迭代实现？

A: 使用显式栈模拟递归过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def backtrack_iterative():
    stack = [(初始状态)]
    result = []
    
    while stack:
        state = stack.pop()
        if 满足结束条件:
            result.append(state)
            continue
        
        for choice in choices:
            if 满足约束:
                new_state = 更新状态(state, choice)
                stack.append(new_state)
    
    return result

迭代实现的优势是避免了栈溢出，但代码通常更复杂，状态管理也更困难。

Q10: 回溯算法可以解决动态规划问题吗？

A: 理论上可以，但不推荐。回溯算法会探索所有可能的路径，时间复杂度通常是指数级的。动态规划通过记忆化和状态转移，将时间复杂度降低到多项式级别。

例如， 0-1 背包问题可以用回溯解决（），但用动态规划可以优化到 。只有在需要找出所有解（而不是最优解）时，回溯算法才有优势。

Q11: 如何调试回溯算法？

A: 调试回溯算法的几个技巧：

  1. 打印路径和状态：在关键位置打印 path、used 等状态变量
  2. 使用调试器：设置断点，单步执行，观察状态变化
  3. 可视化搜索树：画出问题的搜索树，理解算法的执行流程
  4. 小规模测试：先用小规模数据测试，验证逻辑正确性
  5. 对比结果：与已知正确答案对比，找出差异

Q12: 回溯算法的时间复杂度总是指数级的吗？

A: 不一定。虽然回溯算法在最坏情况下通常是指数级复杂度，但通过有效的剪枝，实际运行时间可能远小于理论最坏情况。

例如， N 皇后问题的理论复杂度是 ，但由于约束条件的存在，实际搜索的节点数远小于 。对于 ，理论上有 种可能，但实际只需要搜索约 2000 个节点就能找到所有解。

Q13: 如何选择回溯算法的数据结构？

A: 选择合适的数据结构可以提升效率：

  • 路径存储：使用列表 list，支持高效的 append 和 pop
  • 已访问标记：使用集合 set 或布尔数组，根据操作频率选择
  • 约束检查：使用集合可以 时间检查，比列表更高效
  • 去重：使用集合去重，或排序后使用剪枝

例如，在全排列问题中，如果频繁检查数字是否已使用，用集合比列表更高效。

Q14: 回溯算法可以并行化吗？

A: 可以，但需要谨慎设计。回溯算法的并行化主要有两种方式：

  1. 任务级并行：将搜索树的不同分支分配给不同线程/进程
  2. 数据级并行：并行处理同一层的多个选择

并行化的挑战：

  • 负载均衡：不同分支的搜索时间可能差异很大
  • 共享状态：需要同步访问共享的结果集
  • 开销：线程/进程创建和通信的开销可能抵消并行化的收益

对于大规模问题，并行化可以显著提升性能，但需要仔细设计以避免竞争条件和性能瓶颈。

总结

回溯算法是解决组合优化问题的强大工具。掌握回溯算法的要点：

  1. 理解三要素：选择、约束、目标
  2. 掌握模板：熟练运用回溯模板解决各类问题
  3. 学会剪枝：通过合理的剪枝大幅提升效率
  4. 注意细节：状态恢复、结果复制、去重处理等

通过大量练习，回溯算法会成为你解决 LeetCode 问题的得力助手。记住：回溯算法的本质是"试错"，通过系统地探索所有可能性，最终找到所有解。

  • 本文标题：LeetCode（八）—— 回溯算法
  • 本文作者：Chen Kai
  • 创建时间：2020-02-23 16:00:00
  • 本文链接：https://www.chenk.top/LeetCode%EF%BC%88%E5%85%AB%EF%BC%89%E2%80%94%E2%80%94-%E5%9B%9E%E6%BA%AF%E7%AE%97%E6%B3%95/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
 评论