LeetCode（五）—— 二分查找

二分查找是算法学习中的经典话题，也是 LeetCode 中高频出现的题型。看似简单的“折半查找”，在实际应用中却有不少细节需要处理：边界条件、循环终止、索引更新……这些细节往往决定了代码的正确性。本文将从原理出发，系统梳理二分查找的核心思想、模板实现和常见题型，帮助你在 LeetCode 中游刃有余。

二分查找的核心思想

二分查找（ Binary Search）是一种在有序数组中查找特定元素的算法。它的核心思想可以用一句话概括：通过比较中间元素与目标值，每次将搜索范围缩小一半。

为什么需要有序数组？

二分查找之所以高效，是因为它利用了数组的有序性。假设我们在一个长度为的有序数组中查找目标值：

暴力查找：最坏情况下需要遍历整个数组，时间复杂度为
二分查找：每次比较后可以排除一半的元素，时间复杂度为

当时，暴力查找最多需要次比较，而二分查找最多只需要次（因为）。当增大到时，这个差距会更加明显。

算法流程

二分查找的基本流程如下：

初始化：设置左右边界 left 和 right
循环条件：当 left <= right（或 left < right）时继续
计算中点：mid = (left + right) / 2 或 mid = left + (right - left) / 2
比较判断：
- 如果 nums[mid] == target，找到目标，返回 mid
- 如果 nums[mid] < target，目标在右半部分，更新 left = mid + 1
- 如果 nums[mid] > target，目标在左半部分，更新 right = mid - 1
未找到：循环结束后仍未找到，返回 -1

时间复杂度分析

二分查找的时间复杂度是，空间复杂度是。

时间复杂度推导：

设数组长度为，每次查找后剩余元素数量为：

第 1 次：
第 2 次：
第 3 次：
...
第次：

当剩余元素数量为 1 时，查找结束：

n = 2^{k-1} $$

k = _2 n + 1 $$

因此，最坏情况下需要次比较，时间复杂度为。

边界处理：左闭右开 vs 左闭右闭

二分查找的实现有两种常见的区间定义方式：左闭右开 [left, right) 和 左闭右闭 [left, right]。选择不同的区间定义会影响循环条件、索引更新和边界处理。

左闭右闭区间 `[left, right]`

在这种定义下，left 和 right 都指向有效的数组索引，区间包含两端。

特点：

初始值：left = 0, right = n - 1
循环条件：left <= right（因为 left == right 时区间仍有效）
索引更新：left = mid + 1, right = mid - 1

代码模板：

def binary_search(nums, target):
    left, right = 0, len(nums) - 1  # 左闭右闭
  
    while left <= right:  # 注意是 <=
        mid = left + (right - left) // 2
      
        if nums[mid] == target:
            return mid
        elif nums[mid] < target:
            left = mid + 1  # 目标在右半部分
        else:
            right = mid - 1  # 目标在左半部分
  
    return -1  # 未找到

示例：在 [1, 2, 3, 4, 5] 中查找 3

初始：left=0, right=4，区间 [0, 4] 包含 5 个元素
mid=2, nums[2]=3，找到目标

左闭右开区间 `[left, right)`

在这种定义下，left 指向有效索引，right 指向“边界外”，区间不包含右端点。

特点：

初始值：left = 0, right = n（注意 right 是数组长度）
循环条件：left < right（因为 left == right 时区间为空）
索引更新：left = mid + 1, right = mid（注意 right 不 -1）

代码模板：

def binary_search(nums, target):
    left, right = 0, len(nums)  # 左闭右开
  
    while left < right:  # 注意是 <
        mid = left + (right - left) // 2
      
        if nums[mid] == target:
            return mid
        elif nums[mid] < target:
            left = mid + 1  # 目标在右半部分
        else:
            right = mid  # 注意不 -1，因为 right 是开区间
  
    return -1  # 未找到

示例：在 [1, 2, 3, 4, 5] 中查找 3

初始：left=0, right=5，区间 [0, 5) 包含 5 个元素
mid=2, nums[2]=3，找到目标

两种方式的对比

特性	左闭右闭 `[left, right]`	左闭右开 `[left, right)`
初始 `right`	`len(nums) - 1`	`len(nums)`
循环条件	`left <= right`	`left < right`
`right` 更新	`right = mid - 1`	`right = mid`
区间含义	包含两端	不包含右端
适用场景	传统二分查找	边界查找、插入位置

选择建议：

左闭右闭：更直观，适合基础二分查找
左闭右开：在处理边界问题时更方便，如“查找插入位置”

防止整数溢出

计算中点时，推荐使用 mid = left + (right - left) // 2 而不是 mid = (left + right) // 2。

原因：当 left 和 right 都很大时，left + right 可能超出整数范围导致溢出。而 left + (right - left) // 2 等价于 (left + right) // 2，但避免了溢出风险。

二分查找模板

根据不同的应用场景，二分查找可以分为三种模板：基础版、左边界查找和右边界查找。

模板一：基础二分查找

适用场景：查找目标值在数组中的位置（假设数组中存在且唯一）。

def binary_search(nums, target):
    """
    基础二分查找：查找目标值的位置
    返回：目标值的索引，不存在返回 -1
    """
    left, right = 0, len(nums) - 1
  
    while left <= right:
        mid = left + (right - left) // 2
      
        if nums[mid] == target:
            return mid
        elif nums[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
  
    return -1

模板二：查找左边界

适用场景：查找目标值的第一个出现位置（数组中可能有重复元素）。

关键点：

当 nums[mid] == target 时，不立即返回，而是继续向左查找
循环结束后，left 指向第一个大于等于 target 的位置

def find_left_boundary(nums, target):
    """
    查找左边界：返回目标值的第一个出现位置
    返回：第一个出现位置的索引，不存在返回 -1
    """
    left, right = 0, len(nums) - 1
  
    while left <= right:
        mid = left + (right - left) // 2
      
        if nums[mid] < target:
            left = mid + 1
        else:  # nums[mid] >= target
            right = mid - 1  # 继续向左查找
  
    # 检查 left 是否越界，以及 nums[left] 是否等于 target
    if left >= len(nums) or nums[left] != target:
        return -1
  
    return left

使用左闭右开区间的版本（更简洁）：

def find_left_boundary(nums, target):
    """
    查找左边界（左闭右开版本）
    """
    left, right = 0, len(nums)
  
    while left < right:
        mid = left + (right - left) // 2
      
        if nums[mid] < target:
            left = mid + 1
        else:  # nums[mid] >= target
            right = mid  # 注意： right = mid，不 -1
  
    # left 指向第一个大于等于 target 的位置
    if left == len(nums) or nums[left] != target:
        return -1
  
    return left

模板三：查找右边界

适用场景：查找目标值的最后一个出现位置（数组中可能有重复元素）。

关键点：

当 nums[mid] == target 时，不立即返回，而是继续向右查找
循环结束后，right 指向最后一个小于等于 target 的位置

def find_right_boundary(nums, target):
    """
    查找右边界：返回目标值的最后一个出现位置
    返回：最后一个出现位置的索引，不存在返回 -1
    """
    left, right = 0, len(nums) - 1
  
    while left <= right:
        mid = left + (right - left) // 2
      
        if nums[mid] > target:
            right = mid - 1
        else:  # nums[mid] <= target
            left = mid + 1  # 继续向右查找
  
    # 检查 right 是否越界，以及 nums[right] 是否等于 target
    if right < 0 or nums[right] != target:
        return -1
  
    return right

使用左闭右开区间的版本：

def find_right_boundary(nums, target):
    """
    查找右边界（左闭右开版本）
    """
    left, right = 0, len(nums)
  
    while left < right:
        mid = left + (right - left) // 2
      
        if nums[mid] > target:
            right = mid
        else:  # nums[mid] <= target
            left = mid + 1
  
    # right - 1 指向最后一个小于等于 target 的位置
    if right == 0 or nums[right - 1] != target:
        return -1
  
    return right - 1

模板选择指南

场景	使用的模板
查找唯一目标值	模板一：基础二分查找
查找第一个出现位置	模板二：查找左边界
查找最后一个出现位置	模板三：查找右边界
查找插入位置	模板二：查找左边界（返回 `left`）

经典 LeetCode 题目

题目一： 704. 二分查找

题目描述：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例：

1
2
3

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

分析：这是最基础的二分查找问题，直接使用模板一即可。

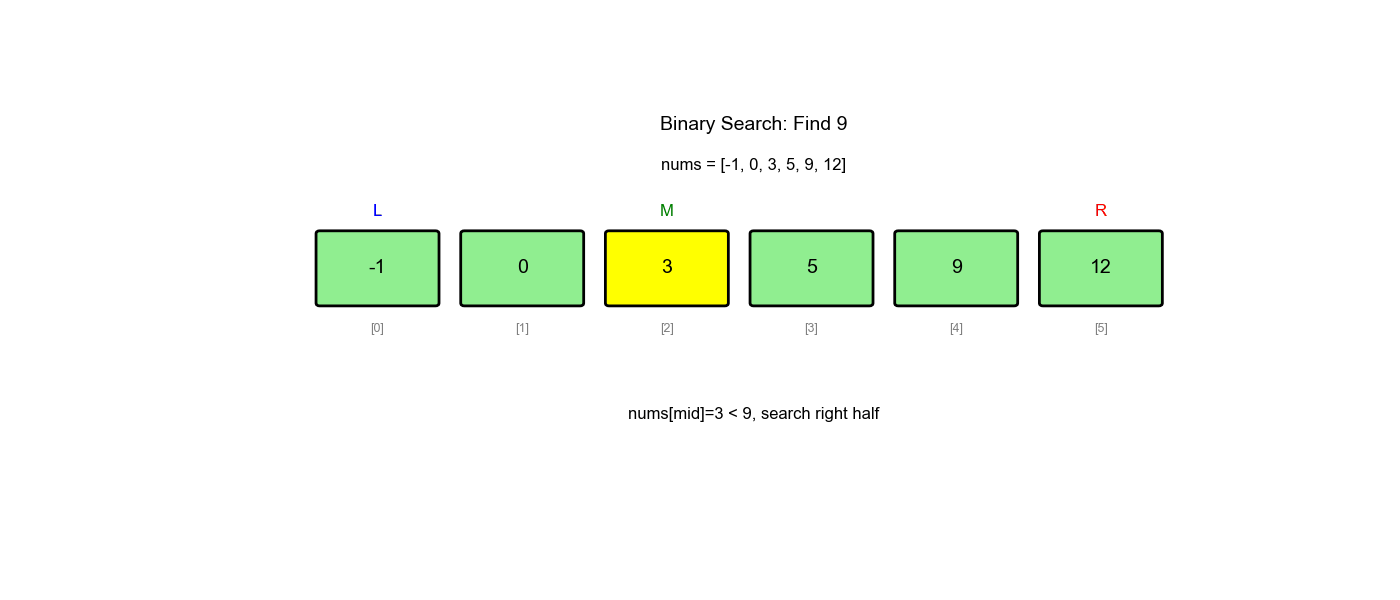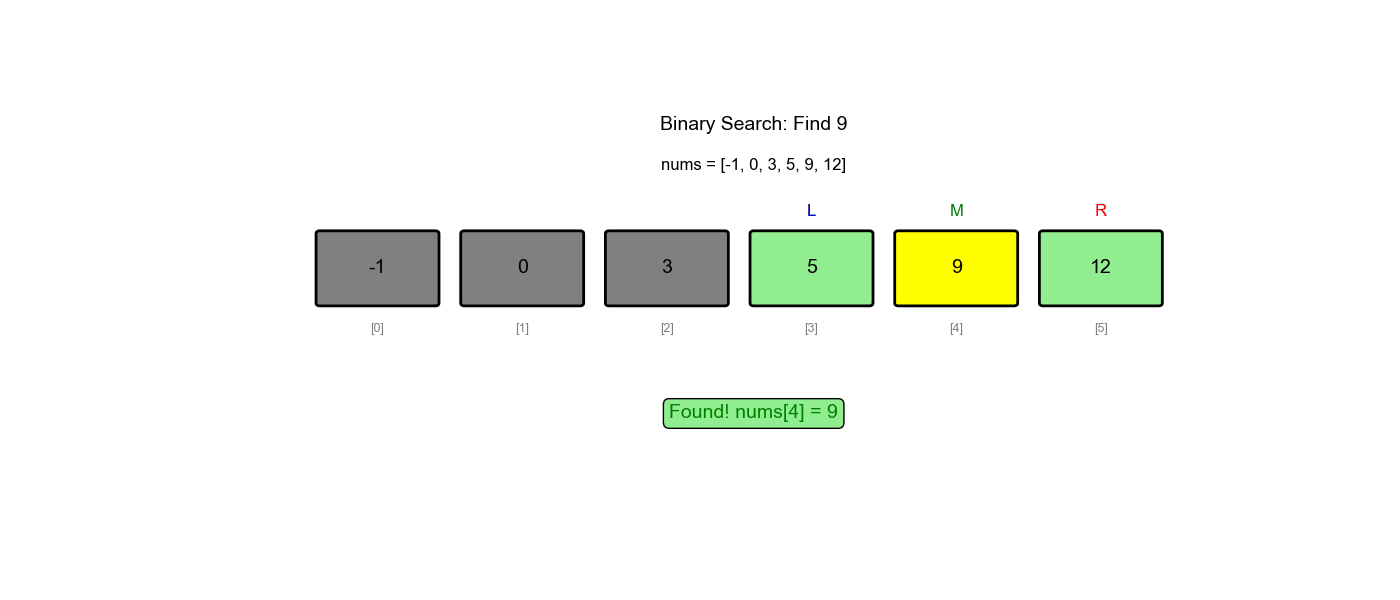
代码实现：

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
      
        while left <= right:
            mid = left + (right - left) // 2
          
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
      
        return -1

时间复杂度：空间复杂度：

题目二： 35. 搜索插入位置

题目描述：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

示例：

输入: nums = [1,3,5,6], target = 5
输出: 2

输入: nums = [1,3,5,6], target = 2
输出: 1

分析：这道题本质上是查找第一个大于等于目标值的位置，可以使用查找左边界的模板。

思路：

如果目标值存在，返回其索引
如果目标值不存在，返回它应该插入的位置（即第一个大于它的元素的位置）

代码实现：

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums)
      
        while left < right:
            mid = left + (right - left) // 2
          
            if nums[mid] < target:
                left = mid + 1
            else:
                right = mid
      
        return left

解释：

当 nums[mid] < target 时，目标值在右半部分，left = mid + 1
当 nums[mid] >= target 时，mid 可能是答案，但需要继续向左查找，right = mid
循环结束后，left 指向第一个大于等于 target 的位置，这正是我们要找的插入位置

时间复杂度：空间复杂度：

题目三： 33. 搜索旋转排序数组

题目描述：整数数组 nums 按升序排列，数组中的值互不相同。在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转。例如，[0,1,2,4,5,6,7] 在下标 3 处旋转后变为 [4,5,6,7,0,1,2]。给你旋转后的数组 nums 和一个整数 target，如果 nums 中存在这个目标值 target，则返回它的下标，否则返回 -1。

示例：

1 2	输入: nums = [4,5,6,7,0,1,2], target = 0 输出: 4

分析：虽然数组被旋转了，但它仍然具有部分有序性。可以通过判断 nums[mid] 与 nums[left] 的关系来确定哪一半是有序的。

思路：

计算中点 mid
判断 nums[left] 到 nums[mid] 是否有序：
- 如果 nums[left] <= nums[mid]，说明左半部分有序
  - 如果 target 在 [nums[left], nums[mid]] 范围内，在左半部分查找
  - 否则在右半部分查找
- 否则右半部分有序
  - 如果 target 在 [nums[mid], nums[right]] 范围内，在右半部分查找
  - 否则在左半部分查找

代码实现：

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
      
        while left <= right:
            mid = left + (right - left) // 2
          
            if nums[mid] == target:
                return mid
          
            # 判断左半部分是否有序
            if nums[left] <= nums[mid]:
                # 左半部分有序
                if nums[left] <= target < nums[mid]:
                    # target 在左半部分
                    right = mid - 1
                else:
                    # target 在右半部分
                    left = mid + 1
            else:
                # 右半部分有序
                if nums[mid] < target <= nums[right]:
                    # target 在右半部分
                    left = mid + 1
                else:
                    # target 在左半部分
                    right = mid - 1
      
        return -1

关键点：

nums[left] <= nums[mid] 判断左半部分是否有序（注意是 <=，因为 left == mid 时只有一个元素，也算有序）
在有序部分判断 target 是否在范围内时，要注意边界条件

时间复杂度：空间复杂度：

题目四： 162. 寻找峰值

题目描述：峰值元素是指其值严格大于左右相邻值的元素。给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。可以假设 nums[-1] = nums[n] = -\infty。

示例：

1
2
3

输入: nums = [1,2,3,1]
输出: 2
解释: 3 是峰值元素，你的函数应该返回其索引 2 。

分析：只要沿着上升的方向走，一定能找到峰值。

思路：

如果 nums[mid] < nums[mid + 1]，说明右边有更大的值，峰值在右半部分
否则，峰值在左半部分（包括 mid 本身）

代码实现：

class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        left, right = 0, len(nums) - 1
      
        while left < right:
            mid = left + (right - left) // 2
          
            if nums[mid] < nums[mid + 1]:
                # 右边有更大的值，峰值在右半部分
                left = mid + 1
            else:
                # 峰值在左半部分（包括 mid）
                right = mid
      
        return left

解释：

使用 left < right 而不是 left <= right，因为需要比较 nums[mid] 和 nums[mid + 1]，要确保 mid + 1 不越界
当 nums[mid] < nums[mid + 1] 时，说明右边有上升趋势，峰值一定在右边
否则，峰值在左边（可能是 mid 本身）

时间复杂度：空间复杂度：

题目五： 74. 搜索二维矩阵

题目描述：编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列
每行的第一个整数大于前一行的最后一个整数

示例：

1 2	输入: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出: true

分析：这个二维矩阵可以看作一个一维有序数组。可以：

先确定目标值在哪一行（通过比较每行的第一个元素）
再在该行中进行二分查找

方法一：两次二分查找

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
      
        # 第一步：确定在哪一行
        row_left, row_right = 0, m - 1
        while row_left <= row_right:
            row_mid = row_left + (row_right - row_left) // 2
            if matrix[row_mid][0] == target:
                return True
            elif matrix[row_mid][0] < target:
                row_left = row_mid + 1
            else:
                row_right = row_mid - 1
      
        # row_right 指向目标值所在的行（如果存在）
        if row_right < 0:
            return False
      
        # 第二步：在该行中查找
        target_row = row_right
        col_left, col_right = 0, n - 1
        while col_left <= col_right:
            col_mid = col_left + (col_right - col_left) // 2
            if matrix[target_row][col_mid] == target:
                return True
            elif matrix[target_row][col_mid] < target:
                col_left = col_mid + 1
            else:
                col_right = col_mid - 1
      
        return False

方法二：一次二分查找（将二维矩阵视为一维数组）

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        left, right = 0, m * n - 1
      
        while left <= right:
            mid = left + (right - left) // 2
            # 将一维索引转换为二维坐标
            row = mid // n
            col = mid % n
          
            if matrix[row][col] == target:
                return True
            elif matrix[row][col] < target:
                left = mid + 1
            else:
                right = mid - 1
      
        return False

方法二的优势：只需要一次二分查找，代码更简洁。

时间复杂度：空间复杂度：

二分答案技巧

二分答案（ Binary Search on Answer）是一种常见的解题技巧，适用于在答案范围内进行二分查找的问题。这类问题的特点是：

答案在一个确定的范围内
对于某个答案值，可以判断它是“太大”还是“太小”
答案具有单调性

适用场景

最小化最大值：如“将数组分成 k 个子数组，使得最大子数组和最小”
最大化最小值：如“在数组中放置 k 个元素，使得最小间距最大”
判定性问题：如“是否存在某种方案满足条件”

解题模板

def binary_search_answer():
    # 1. 确定答案的范围
    left, right = min_answer, max_answer
  
    # 2. 二分查找答案
    while left < right:  # 或 left <= right，取决于问题
        mid = left + (right - left) // 2
      
        # 3. 判断 mid 是否满足条件
        if check(mid):
            # mid 满足条件，尝试更小的答案（或更大的，取决于问题）
            right = mid  # 或 left = mid + 1
        else:
            # mid 不满足条件，需要更大的答案（或更小的）
            left = mid + 1  # 或 right = mid - 1
  
    return left  # 或 right，取决于问题

经典例题： 875. 爱吃香蕉的珂珂

题目描述：珂珂喜欢吃香蕉。这里有 n 堆香蕉，第 i 堆有 piles[i] 根香蕉。警卫已经离开了，将在 h 小时后回来。珂珂可以决定她吃香蕉的速度 k（单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 k 根。如果这堆香蕉少于 k 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。返回她可以在 h 小时内吃掉所有香蕉的最小速度 k。

示例：

1 2	输入: piles = [3,6,7,11], h = 8 输出: 4

分析：

答案范围：最小速度是，最大速度是（因为速度再大也没有意义）
判断函数：给定速度 k，计算吃完所有香蕉需要的时间，判断是否
单调性：速度越大，所需时间越少；我们要找最小的满足条件的速度

代码实现：

class Solution:
    def minEatingSpeed(self, piles: List[int], h: int) -> int:
        left, right = 1, max(piles)
      
        while left < right:
            mid = left + (right - left) // 2
          
            # 计算以速度 mid 吃完所有香蕉需要的时间
            time = sum((pile + mid - 1) // mid for pile in piles)
          
            if time <= h:
                # 时间满足要求，尝试更小的速度
                right = mid
            else:
                # 时间不够，需要更大的速度
                left = mid + 1
      
        return left

关键点：

(pile + mid - 1) // mid 是向上取整的技巧，等价于
使用 left < right 和 right = mid，确保找到最小的满足条件的值

时间复杂度：，其中是数组长度 空间复杂度：

常见错误与调试

错误一：死循环

原因：循环条件或索引更新不当，导致 left 和 right 无法收敛。

示例：

# 错误示例
while left < right:
    mid = left + (right - left) // 2
    if nums[mid] < target:
        left = mid  # 错误：应该是 left = mid + 1
    else:
        right = mid

修复：确保每次循环都能缩小搜索范围。

错误二：索引越界

原因：在访问 nums[mid] 或 nums[left]、nums[right] 时没有检查边界。

示例：

# 错误示例
def find_left_boundary(nums, target):
    left, right = 0, len(nums) - 1
    while left <= right:
        # ...
    return left  # 错误：没有检查 left 是否越界

修复：在返回前检查索引是否在有效范围内。

错误三：整数溢出

原因：使用 (left + right) // 2 计算中点，当 left 和 right 很大时可能溢出。

修复：使用 left + (right - left) // 2。

错误四：边界条件处理不当

原因：没有正确处理目标值不存在、数组为空、目标值在边界外等情况。

调试技巧：

打印中间状态：

while left <= right:
    mid = left + (right - left) // 2
    print(f"left={left}, right={right}, mid={mid}, nums[mid]={nums[mid]}")
    # ...

测试边界情况：
- 空数组
- 只有一个元素
- 目标值在数组最左/最右
- 目标值不存在且小于最小值/大于最大值
使用断言：

1 2	assert 0 <= left < len(nums), f"left={left} out of range" assert 0 <= right < len(nums), f"right={right} out of range"

❓ Q&A: 二分查找常见问题

Q1: 什么时候使用 `left <= right`，什么时候使用 `left < right`？

left <= right：适用于左闭右闭区间 [left, right]。当 left == right 时，区间仍包含一个元素，需要继续查找。
left < right：适用于左闭右开区间 [left, right)。当 left == right 时，区间为空，查找结束。

选择哪种方式主要看你的区间定义。如果使用左闭右闭，就用 <=；如果使用左闭右开，就用 <。

Q2: 为什么查找左边界时，`nums[mid] == target` 不直接返回？

A: 因为我们要找的是第一个出现的位置。如果直接返回，可能返回的是中间某个位置，而不是最左边的。正确的做法是继续向左查找，直到找到最左边的位置。

例如，在 [1, 2, 2, 2, 3] 中查找 2：

如果 mid=2 时直接返回，得到索引 2
但第一个 2 的索引是 1，所以应该继续向左查找

Q3: 二分查找一定比线性查找快吗？

A: 不一定。二分查找的时间复杂度是，线性查找是。但是：

预处理成本：二分查找要求数组有序，如果数组无序，需要先排序（）。例如，如果只需要查找一次，排序的成本可能超过直接线性查找的成本。
数据量小：当数据量很小时（如），线性查找可能更快，因为常数因子更小。实际测试表明，当时，线性查找通常更快。
缓存友好性：线性查找对 CPU 缓存更友好，访问连续内存。二分查找的跳跃访问可能导致缓存未命中，影响性能。

实际例子：

场景一：数组已有序，需要查找 1000 次 → 二分查找更优（预处理一次，后续查找都是）
场景二：数组无序，只查找 1 次 → 线性查找更优（避免排序的成本）
场景三：数组很小（）→ 线性查找可能更快（常数因子更小）

因此，如果数组已经有序或需要多次查找，二分查找更优；如果只查找一次且数组无序，线性查找可能更合适。

Q4: 如何处理有重复元素的数组？

A: 使用查找左边界或右边界的模板：

查找第一个出现位置：使用查找左边界的模板
查找最后一个出现位置：使用查找右边界的模板
查找所有出现位置：先找左边界，再找右边界，然后返回 [left_boundary, right_boundary]

Q5: 二分查找可以用于链表吗？

A: 理论上可以，但不推荐。因为：

链表不支持随机访问，访问 mid 节点需要时间
总时间复杂度会变成，不如直接遍历

如果一定要用，可以先遍历一次链表，将节点指针存入数组，然后在数组中进行二分查找。

Q6: 如何判断一个问题是否可以用二分查找？

A: 满足以下条件之一即可：

有序性：数组（或答案范围）具有单调性
可判定性：对于某个值，可以判断它是“太大”还是“太小”
范围性：答案在一个确定的范围内

例如：

有序数组查找 → 满足条件 1
旋转数组查找 → 满足条件 1（部分有序）
二分答案问题 → 满足条件 2 和 3

Q7: `mid = (left + right) // 2` 和 `mid = left + (right - left) // 2` 有什么区别？

A: 在 Python 中，两者在大多数情况下等价。但在其他语言（如 C++、 Java）中：

(left + right) // 2 可能在 left + right 很大时溢出
left + (right - left) // 2 避免了溢出风险

建议：统一使用 left + (right - left) // 2，这样代码更安全、可移植。

Q8: 二分查找的变种有哪些？

A: 常见的变种包括：

查找插入位置： 35. 搜索插入位置
查找边界： 34. 在排序数组中查找元素的第一个和最后一个位置
旋转数组查找： 33. 搜索旋转排序数组、 81. 搜索旋转排序数组 II
二维二分： 74. 搜索二维矩阵、 240. 搜索二维矩阵 II
二分答案： 875. 爱吃香蕉的珂珂、 410. 分割数组的最大值
峰值查找： 162. 寻找峰值

Q9: 如何记忆二分查找的模板？

A: 建议：

理解原理：理解为什么这样写，而不是死记硬背
固定一种写法：选择一种区间定义（推荐左闭右开），然后一直用这种写法
多练习：通过刷题加深理解，形成肌肉记忆
画图辅助：遇到边界问题时，画图帮助理解

Q10: 二分查找在实际开发中的应用场景？

数据库索引： B+ 树索引使用二分查找定位数据页。例如， MySQL 的 InnoDB 引擎在查找索引时，会从根节点开始，通过二分查找快速定位到目标数据所在的叶子节点。
系统调用：如 Linux 内核中的 bsearch() 函数，用于在有序数组中快速查找。许多系统库函数内部都使用二分查找优化性能。
游戏开发：在有序数据中查找（如排行榜、装备属性）。例如，在排行榜系统中，需要根据分数快速定位玩家的排名，二分查找可以高效完成这个任务。
算法优化：将的查找优化为。例如，在动态规划问题中，如果状态转移需要查找，可以用二分查找将时间复杂度从优化到。
数值计算：求解方程的根、优化问题等。例如，使用二分法求解的根，当函数单调时，二分查找可以快速收敛到解。

变体与扩展问题

变体一：在旋转数组中查找

旋转数组虽然整体无序，但至少有一半是有序的，可以利用这个性质进行二分查找。

关键技巧：

判断哪一半是有序的：nums[left] <= nums[mid] 说明左半部分有序
在有序部分判断目标是否在范围内
如果不在有序部分，在无序部分继续查找

扩展题目：

1. 搜索旋转排序数组（无重复）
1. 搜索旋转排序数组 II（有重复，需要特殊处理）
1. 寻找旋转排序数组中的最小值
1. 寻找旋转排序数组中的最小值 II（有重复）

变体二：二维二分查找

二维矩阵也可以进行二分查找，通过将二维索引转换为一维索引。

转换公式：

一维索引 idx → 二维坐标：row = idx // n，col = idx % n
二维坐标 (row, col) → 一维索引：idx = row * n + col

扩展题目：

1. 搜索二维矩阵（每行第一个数大于上一行最后一个数）
1. 搜索二维矩阵 II（每行每列都递增，更复杂）

变体三：二分答案

当答案在一个范围内，且可以判断某个值是否满足条件时，可以用二分查找在答案范围内搜索。

解题步骤：

确定答案的范围 [left, right]
写判断函数 check(mid)：判断 mid 是否满足条件
根据判断结果缩小搜索范围
返回最优答案

经典题目：

1. 爱吃香蕉的珂珂
1. 分割数组的最大值
1. 在 D 天内送达包裹的能力
1. 制作 m 束花所需的最少天数

变体四：查找峰值

即使数组不完全有序，只要满足某些性质（如单峰、双峰），也可以用二分查找。

关键思想：沿着上升的方向走，一定能找到峰值。

扩展题目：

1. 寻找峰值
1. 山脉数组的峰顶索引

常见错误与调试技巧

错误一：死循环

原因：循环条件与边界更新不匹配。

错误示例：

# 错误：使用 left < right 但 right = mid - 1
while left < right:
    mid = left + (right - left) // 2
    if nums[mid] < target:
        left = mid + 1
    else:
        right = mid - 1  # 可能导致死循环

修复方法：

如果使用 left <= right，用 right = mid - 1
如果使用 left < right，用 right = mid

错误二：索引越界

原因：返回前没有检查索引是否在有效范围内。

错误示例：

def find_left_boundary(nums, target):
    left, right = 0, len(nums) - 1
    while left <= right:
        # ...
    return left  # 错误：没有检查 left 是否越界

修复方法：

# 检查索引是否越界
if left >= len(nums) or nums[left] != target:
    return -1
return left

错误三：整数溢出

原因：使用 (left + right) // 2 计算中点。

修复方法：统一使用 left + (right - left) // 2

错误四：边界条件处理不当

常见边界情况：

空数组：len(nums) == 0
单个元素：len(nums) == 1
目标值在数组最左/最右
目标值不存在且小于最小值/大于最大值
数组中有重复元素

调试技巧：

打印中间状态：

while left <= right:
    mid = left + (right - left) // 2
    print(f"left={left}, right={right}, mid={mid}, nums[mid]={nums[mid]}")
    # ...

使用断言：

1 2	assert 0 <= left < len(nums), f"left={left} out of range" assert 0 <= right < len(nums), f"right={right} out of range"

测试用例：
- []（空数组）
- [1]（单个元素）
- [1, 2, 3]， target = 1（在边界）
- [1, 2, 3]， target = 0（不存在且小于最小值）
- [1, 2, 2, 2, 3]， target = 2（有重复）

实战建议

如何快速识别二分查找问题

看到以下特征时，考虑二分查找：

有序数组：数组已经排序（或可以排序）
查找目标：需要找到某个值、位置、或满足条件的值
时间复杂度要求：要求时间复杂度
答案范围：答案在一个确定的范围内（二分答案）

选择模板的决策树

问题要求什么？
├─ 查找唯一目标值 → 使用标准模板
├─ 查找第一个出现位置 → 使用左边界模板
├─ 查找最后一个出现位置 → 使用右边界模板
└─ 查找插入位置 → 使用左边界模板（返回 left）

解题步骤

确定搜索空间：是在数组中搜索，还是在答案范围内搜索？
选择模板：根据问题要求选择合适的模板
确定循环条件：left <= right 还是 left < right？
写判断逻辑：如何根据 nums[mid] 和 target 的关系更新边界？
处理边界情况：空数组、单个元素、目标不存在等
验证答案：检查返回值的正确性

性能优化建议

提前终止：如果找到目标值，可以立即返回
减少比较次数：合并相似的条件判断
空间优化：如果只需要索引，不需要存储完整数组

与其他算法的结合

二分查找 + 滑动窗口：窗口大小不确定时，用二分查找确定最优大小
二分查找 + 动态规划： DP 状态转移需要查找时，用二分优化
二分查找 + 贪心：贪心策略需要验证时，用二分查找答案

总结

二分查找是一种高效且实用的算法，掌握它需要：

理解核心思想：利用有序性，每次排除一半元素
掌握边界处理：理解左闭右开和左闭右闭的区别
熟练使用模板：基础查找、左边界、右边界三种模板
灵活应用：能够识别可以使用二分查找的问题，包括二分答案类问题
注意细节：防止溢出、处理边界条件、避免死循环

通过系统学习和大量练习，你一定能在 LeetCode 中游刃有余地解决二分查找相关的问题。记住：理解原理比记忆模板更重要，只有真正理解了，才能灵活应对各种变种题目。

二分查找在面试中的应用

二分查找是技术面试中的高频考点，不仅考察算法实现能力，还考察对边界条件的处理和对问题本质的理解。掌握以下要点，能帮助你在面试中脱颖而出。

面试官常问的问题类型

基础实现类：直接要求实现二分查找
- 考察点：边界处理、溢出防护、代码规范性
- 示例： LeetCode 704（二分查找）
边界查找类：查找第一个或最后一个出现位置
- 考察点：理解左边界和右边界的区别，处理重复元素
- 示例： LeetCode 34（在排序数组中查找元素的第一个和最后一个位置）
变种问题类：旋转数组、二维矩阵、峰值查找
- 考察点：能否识别可以使用二分查找的场景，灵活应用模板
- 示例： LeetCode 33（搜索旋转排序数组）、 LeetCode 162（寻找峰值）
二分答案类：在答案范围内进行二分查找
- 考察点：能否识别问题的单调性，设计判断函数
- 示例： LeetCode 875（爱吃香蕉的珂珂）、 LeetCode 410（分割数组的最大值）

面试中的常见陷阱

边界条件处理：面试官可能会故意给出边界测试用例
- 空数组：[]
- 单个元素：[1]
- 目标值在边界：[1, 2, 3]， target = 1 或 3
- 目标值不存在：[1, 2, 3]， target = 0 或 4
整数溢出：如果使用 (left + right) // 2，面试官可能会问为什么不用 left + (right - left) // 2
死循环问题：循环条件和边界更新不匹配，导致死循环

面试答题技巧

先确认理解：在开始编码前，先和面试官确认问题的理解，包括：
- 数组是否有序？
- 是否有重复元素？
- 返回值的要求（索引、布尔值、插入位置等）？
说明思路：编码前先说明你的思路，包括：
- 选择哪个模板（标准、左边界、右边界）
- 为什么选择这个模板
- 如何处理边界情况
边写边解释：编码时解释关键步骤，特别是：
- 为什么选择这个循环条件（left <= right vs left < right）
- 为什么这样更新边界（right = mid - 1 vs right = mid）
- 如何防止溢出
测试用例：编码完成后，主动提出测试用例：
- 正常情况：目标值存在
- 边界情况：目标值在边界、不存在、数组为空
- 特殊情况：有重复元素
复杂度分析：主动分析时间和空间复杂度，展示你的算法分析能力

常见面试问题示例

问题：在一个有序数组中查找目标值的第一个出现位置，如果不存在则返回 -1 。

回答思路：

这是典型的左边界查找问题，应该使用左边界模板
使用左闭右开区间 [left, right)，循环条件 left < right
当 nums[mid] >= target 时，right = mid（保留 mid，因为可能是答案）
循环结束后，left 指向第一个大于等于 target 的位置
需要检查 left 是否越界，以及 nums[left] 是否等于 target

代码实现：

def find_first_occurrence(nums, target):
    left, right = 0, len(nums)
  
    while left < right:
        mid = left + (right - left) // 2
      
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid
  
    if left == len(nums) or nums[left] != target:
        return -1
  
    return left

复杂度分析：

时间复杂度：，每次循环排除一半元素
空间复杂度：，只使用了常数个变量

通过这样的回答，既展示了你的代码能力，又体现了你对算法原理的深入理解，这正是面试官希望看到的。

二分查找的核心思想

为什么需要有序数组？

算法流程

时间复杂度分析

边界处理：左闭右开 vs 左闭右闭

左闭右闭区间 [left, right]

左闭右开区间 [left, right)

两种方式的对比

防止整数溢出

二分查找模板

模板一：基础二分查找

模板二：查找左边界

模板三：查找右边界

模板选择指南

经典 LeetCode 题目

题目一： 704. 二分查找

题目二： 35. 搜索插入位置

题目三： 33. 搜索旋转排序数组

题目四： 162. 寻找峰值

题目五： 74. 搜索二维矩阵

二分答案技巧

适用场景

解题模板

经典例题： 875. 爱吃香蕉的珂珂

更多二分答案题目

常见错误与调试

错误一：死循环

错误二：索引越界

错误三：整数溢出

错误四：边界条件处理不当

❓ Q&A: 二分查找常见问题

Q1: 什么时候使用 left <= right，什么时候使用 left < right？

Q2: 为什么查找左边界时，nums[mid] == target 不直接返回？

Q3: 二分查找一定比线性查找快吗？

Q4: 如何处理有重复元素的数组？

Q5: 二分查找可以用于链表吗？

Q6: 如何判断一个问题是否可以用二分查找？

Q7: mid = (left + right) // 2 和 mid = left + (right - left) // 2 有什么区别？

Q8: 二分查找的变种有哪些？

Q9: 如何记忆二分查找的模板？

Q10: 二分查找在实际开发中的应用场景？

变体与扩展问题

变体一：在旋转数组中查找

变体二：二维二分查找

变体三：二分答案

变体四：查找峰值

常见错误与调试技巧

错误一：死循环

错误二：索引越界

错误三：整数溢出

错误四：边界条件处理不当

实战建议

如何快速识别二分查找问题

选择模板的决策树

解题步骤

性能优化建议

与其他算法的结合

总结

二分查找在面试中的应用

面试官常问的问题类型

面试中的常见陷阱

面试答题技巧

常见面试问题示例

左闭右闭区间 `[left, right]`

左闭右开区间 `[left, right)`

Q1: 什么时候使用 `left <= right`，什么时候使用 `left < right`？

Q2: 为什么查找左边界时，`nums[mid] == target` 不直接返回？

Q7: `mid = (left + right) // 2` 和 `mid = left + (right - left) // 2` 有什么区别？