LeetCode（二）—— 双指针技巧

Chen Kai BOSS

2020-01-11 14:00:00 2020-01-11 14:00

算法与数据结构

15.8k 字 60 分钟

双指针是算法面试中最优雅的技巧之一：通过巧妙地维护两个指针之间的位置关系，可以将暴力复杂度降低到，同时保持的空间开销。本文系统性地介绍三种核心模式——对撞指针（从两端向中间收敛）、快慢指针（速度差检测环）和滑动窗口（动态子数组维护）——通过六个经典问题构建完整的双指针思维体系。我们还将深入分析何时选择双指针而非哈希表、如何避免边界错误，以及面试沟通技巧。

系列导航

📚 LeetCode 算法精讲系列（共 10 篇）：

哈希表（两数之和、最长连续序列、字母异位词分组）
→ 双指针技巧（对撞指针、快慢指针、滑动窗口）← 当前文章
链表操作（反转、环检测、合并）
二叉树遍历与递归（中序/前序/后序、最近公共祖先）
动态规划入门（一维/二维 DP 、状态转移）
回溯算法（排列、组合、剪枝）
二分查找进阶（整数/实数二分、答案二分）
栈与队列（单调栈、优先队列、双端队列）
图算法（ BFS/DFS 、拓扑排序、并查集）
贪心与位运算（贪心策略、位操作技巧）

双指针核心概念

为什么需要双指针？

场景：在已排序数组中找到两个数，它们的和等于目标值。

暴力解法：两个嵌套循环枚举所有数对 → 双指针优化：

左指针指向最小值
右指针指向最大值
如果和太小，左指针右移（增加和）
如果和太大，右指针左移（减少和）
复杂度降低到

三种核心模式

模式	指针关系	典型场景	示例问题
对撞指针	从两端向中间移动	排序数组、回文检查	两数之和 II 、盛最多水的容器
快慢指针	以不同速度移动	链表环检测、找中点	环形链表、快乐数
滑动窗口	维护固定/动态区间	子数组/子串问题	无重复字符的最长子串、最小窗口子串

模式一：对撞指针

核心特征

左指针从开头开始
右指针从末尾开始
指针收敛，相互靠近直到相遇
通常用于已排序数组或需要考虑两端的问题

现实类比

想象你在书店，有固定预算买两本书：

你从最便宜的书架开始
你的朋友从最昂贵的书架开始
如果总价太便宜，你向昂贵书籍移动
如果总价太昂贵，朋友向便宜书籍移动
最终你们在恰好符合预算的书架相遇

LeetCode 11: 盛最多水的容器

问题分析

核心难点：如何在时间内找到面积最大的容器，而不是暴力检查所有个可能的容器对。容器的面积由宽度和高度共同决定，宽度是两线之间的距离，高度是较短的那条线。

解题思路：使用对撞指针（从两端向中间收敛）。关键洞察是贪心策略：总是移动较短的那一边。因为面积由较短边决定，移动较长边只会减少宽度而不会增加高度，面积必然减小；而移动较短边虽然宽度也减少，但可能遇到更高的边，面积可能增大。这种策略保证了不会错过最优解。

复杂度分析：

时间复杂度： - 每个元素最多访问一次
空间复杂度： - 仅使用两个指针

关键洞察：贪心策略的正确性基于反证法：如果最优解是，我们的算法会通过移动较短边逐步接近它，不会跳过最优解。

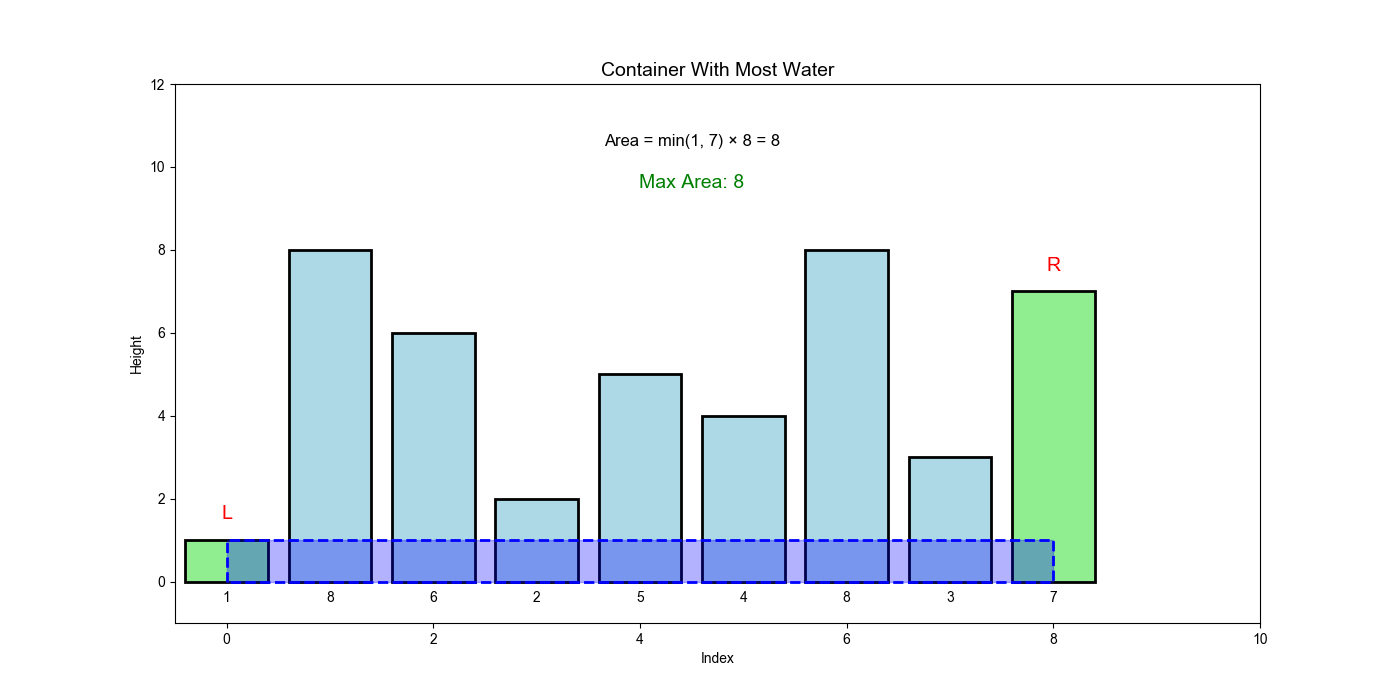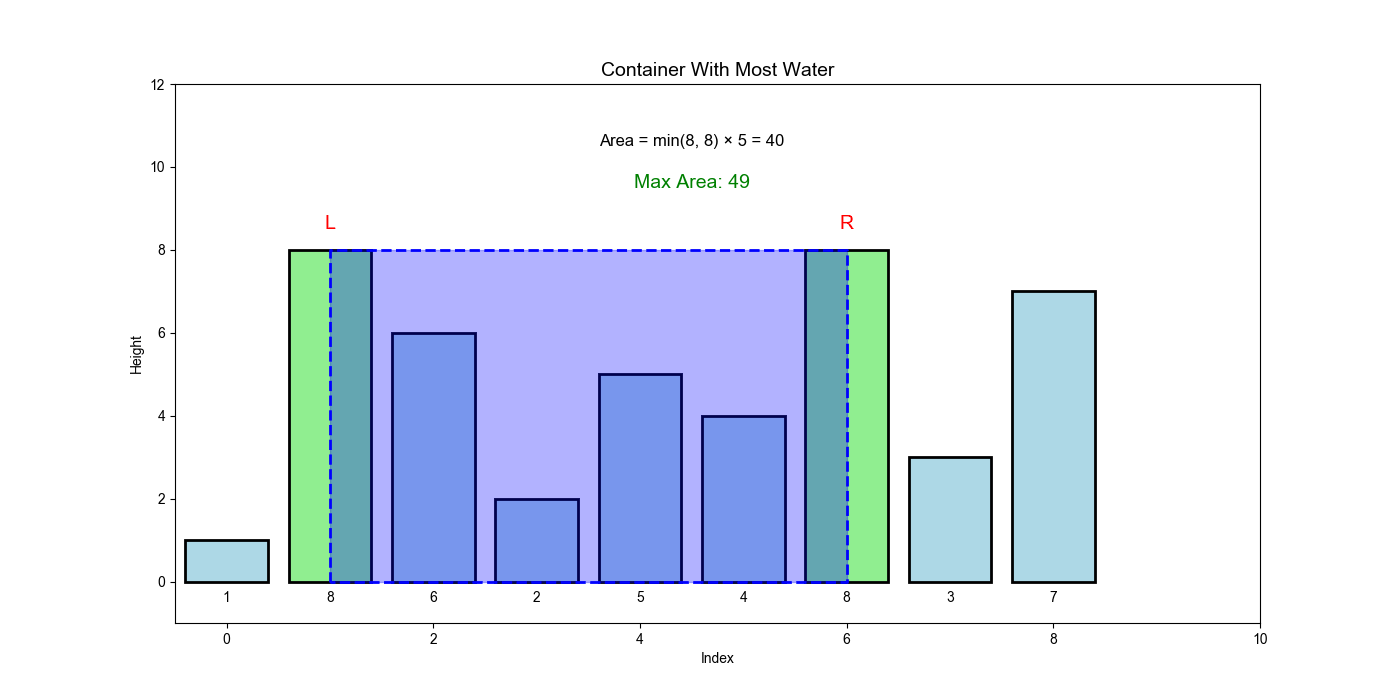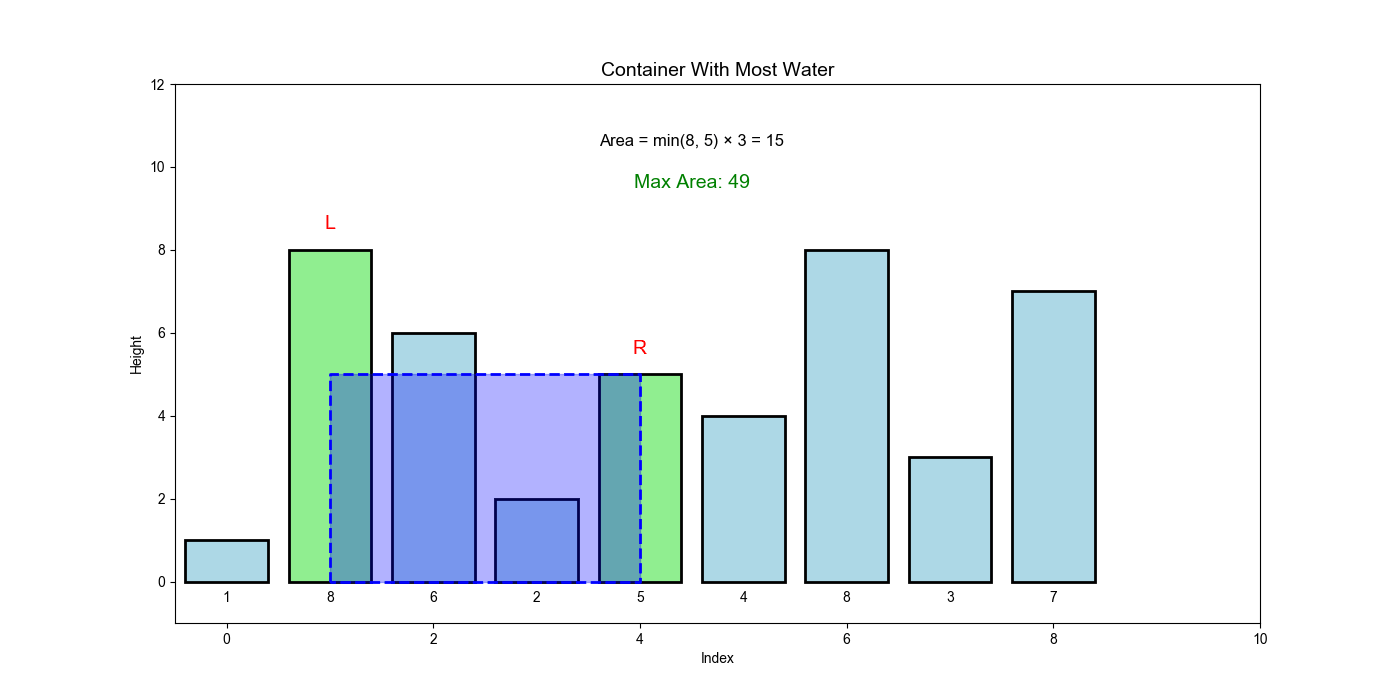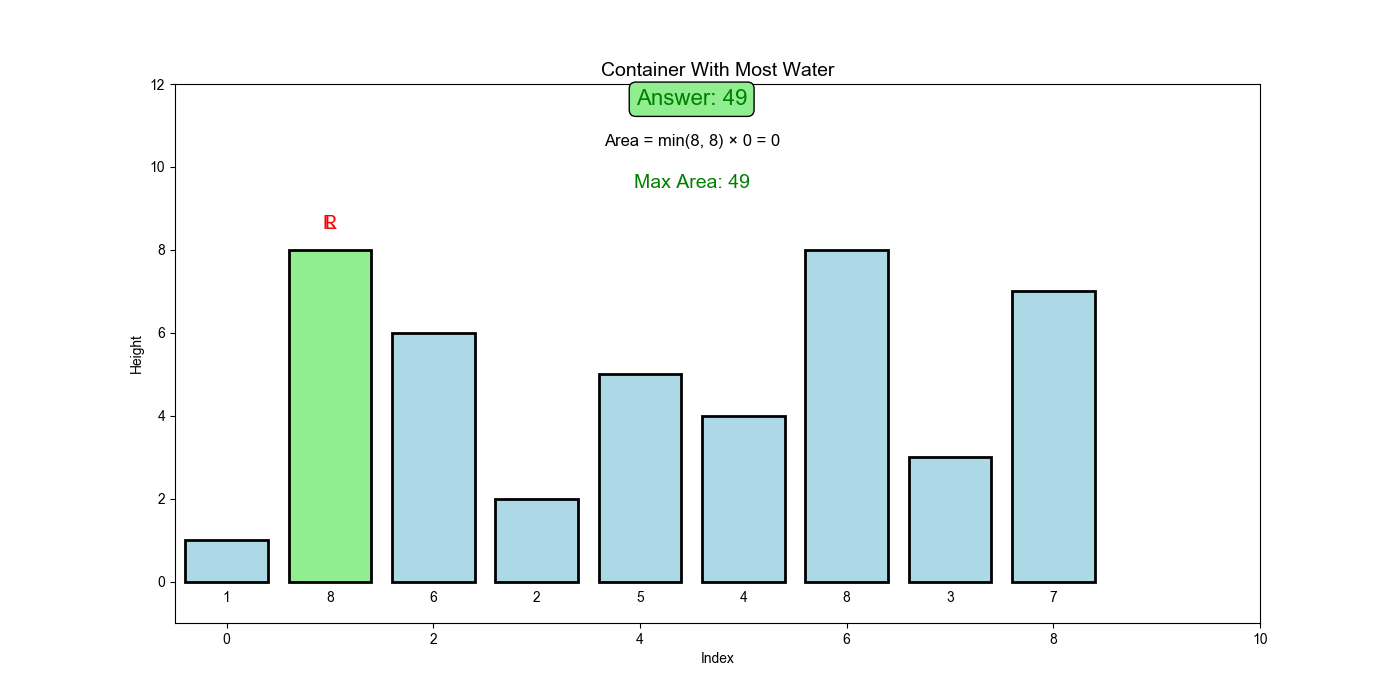
问题描述

给定个非负整数，其中每个代表坐标平面上的一个点。绘制条垂直线，使得线的两个端点位于和。找到两条线，它们与 x 轴一起形成一个容器，能够容纳最多的水。

示例：

输入：height = [1,8,6,2,5,4,8,3,7]
输出：49
解释：位于和的线形成容器，面积 = 约束条件：

核心洞察

面积公式： $面积$ 贪心策略：

从两端开始（最大宽度）
总是移动较短的一边（因为高度由较短的线决定）
移动较长的一边只能减少面积（宽度减少，高度不会增加）

Python 实现

def maxArea(height):
    # 初始化双指针：从两端开始（最大宽度）
    left, right = 0, len(height) - 1
    max_area = 0  # 记录最大面积
  
    # 对撞指针：向中间收敛
    while left < right:
        # 计算当前容器的面积
        # 宽度 = 两线之间的距离
        width = right - left
        # 高度 = 较短的那条线（水会从短边溢出）
        current_height = min(height[left], height[right])
        # 面积 = 宽度 × 高度
        current_area = width * current_height
        # 更新最大面积
        max_area = max(max_area, current_area)
    
        # 关键贪心策略：总是移动较短的那一边
        # 原因：移动较长边只会减少宽度，高度不会增加，面积必然减小
        # 移动较短边虽然宽度减少，但可能遇到更高的边，面积可能增大
        if height[left] < height[right]:
            left += 1   # 左指针右移
        else:
            right -= 1  # 右指针左移
  
    return max_area

Java 实现

class Solution {
    public int maxArea(int[] height) {
        int left = 0, right = height.length - 1;
        int maxArea = 0;
    
        while (left < right) {
            int width = right - left;
            int currentHeight = Math.min(height[left], height[right]);
            int currentArea = width * currentHeight;
            maxArea = Math.max(maxArea, currentArea);
        
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
    
        return maxArea;
    }
}

复杂度分析

时间复杂度：，每个元素最多访问一次
空间复杂度：，仅使用两个指针

深入解读

算法原理：为什么贪心策略是正确的？

核心思想：面积公式是 $面积$ ，其中 $ w = - $。当我们移动指针时：移动较长边：$ w$减少，但不会增加（因为高度由较短边决定），所以面积必然减小 - 移动较短边：$ w $减少，但可能遇到更高的边，$ (h_l, h_r)$可能增加，面积可能增大

因此，只有移动较短边才有找到更大面积的可能。

时间复杂度证明：为什么是 O(n)？

指针移动：left 只能右移，right 只能左移
总移动次数：最多次（两指针相遇时停止）
每次迭代：操作（计算面积、比较、移动指针）
总时间：

空间优化：有没有更省空间的方法？

这个问题已经是空间最优的： - 双指针：空间 - 无法进一步优化：必须存储当前最大面积和两个指针位置

对比其他方法： - 暴力法：空间，但时间 - 动态规划：不适用（无重叠子问题）

常见错误分析

错误类型	错误代码	问题	正确做法
移动较长边	`if height[left] > height[right]: left += 1`	错过最优解	移动较短边
同时移动两边	`left += 1; right -= 1`	可能跳过最优解	只移动一边
忘记更新最大面积	只计算不存储	无法返回答案	`max_area = max(max_area, current_area)`

变体扩展

盛最多水的容器（三维）：扩展到三维空间
接雨水：类似问题，但计算方式不同
最大矩形面积：使用单调栈解决

为什么这个贪心策略是正确的？

反证法证明：假设最优解是，其中 - 如果我们从开始并向移动： - 如果，我们移动左指针 - 所有面积，其中都被考虑 - 关键：移动较短指针是可能找到更大面积的唯一方法 - 移动较长指针必须导致更小的面积（宽度减少，高度不能增加）

数学证明

设 $ h_l = [] $，$ h_r = [] $，假设$ h_l < h_r$。

当前面积：，其中 如果我们移动右指针（错误移动）：

新宽度：（更小）
新高度：（不能超过较短边）
新面积： 如果我们移动左指针（正确移动）：
新宽度：
新高度：可能大于
新面积：，可能更大

结论：只有移动较短指针才有改进的潜力。

常见陷阱

陷阱一：尝试所有数对

# ❌ 暴力 O(n ²)
for i in range(n):
    for j in range(i+1, n):
        area = min(height[i], height[j]) * (j - i)

为什么慢：计算所有个数对

陷阱二：移动较长指针

1
2
3

# ❌ 错误策略
if height[left] > height[right]:
    left += 1

为什么错误：错过潜在的最优解

陷阱三：先排序

问题：排序会破坏原始位置关系，但宽度计算依赖于索引

LeetCode 15: 三数之和

问题分析

核心难点：这道题的关键挑战在于如何高效地找到所有不重复的三元组，避免的暴力枚举。问题要求返回所有解且不能重复，这增加了去重的复杂性。

解题思路：将三数之和转化为两数之和。首先排序数组（允许，因为问题不需要返回索引），然后固定第一个数，对剩余部分使用对撞指针找到两个数，它们的和等于 -nums[i]。关键技巧是三层去重：第一个数、第二个数（左指针）、第三个数（右指针）都需要跳过重复值，确保结果唯一。

复杂度分析： - 时间复杂度： - 排序 + 外层循环 × 内层双指针 - 空间复杂度：到 - 排序栈空间

关键洞察：排序后可以使用双指针，将查找两个数的复杂度从降低到。去重是关键，必须在三个位置都正确处理。

问题描述

给你一个整数数组 nums，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足且 nums[i] + nums[j] + nums[k] = 0。请你返回所有和为 0 且不重复的三元组。

示例：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

约束条件：

核心洞察

转换为两数之和：

排序数组（允许，因为问题不需要索引）
固定第一个数 nums[i]
在剩余部分使用对撞指针找到两个数，它们的和等于 -nums[i]
跳过重复以确保唯一三元组

Python 实现

def threeSum(nums):
    # 排序数组：允许使用双指针， O(n log n)
    # 注意：排序会改变元素位置，但问题不需要返回索引
    nums.sort()  # O(n log n)
    result = []
    n = len(nums)
  
    # 固定第一个数，对剩余部分使用双指针
    for i in range(n - 2):
        # 去重：跳过重复的第一个数
        # 如果当前数和前一个数相同，跳过以避免重复三元组
        if i > 0 and nums[i] == nums[i-1]:
            continue
    
        # 早期终止优化：如果最小数 > 0，所有后续数都是正数
        # 三个正数不可能和为 0，直接退出
        if nums[i] > 0:
            break
    
        # 对剩余两个数使用对撞指针
        left, right = i + 1, n - 1
        # 目标值 = -nums[i]，因为 nums[i] + nums[left] + nums[right] = 0
        target = -nums[i]
    
        while left < right:
            current_sum = nums[left] + nums[right]
        
            if current_sum == target:
                # 找到一组解，添加到结果
                result.append([nums[i], nums[left], nums[right]])
            
                # 关键：跳过重复的第二个数和第三个数
                # 必须在这里跳过，避免重复三元组
                while left < right and nums[left] == nums[left+1]:
                    left += 1  # 跳过所有重复的左指针值
                while left < right and nums[right] == nums[right-1]:
                    right -= 1  # 跳过所有重复的右指针值
            
                # 移动指针继续寻找下一组解
                left += 1
                right -= 1
            elif current_sum < target:
                # 和太小，左指针右移（增加和）
                left += 1
            else:
                # 和太大，右指针左移（减少和）
                right -= 1
  
    return result

复杂度分析

时间复杂度： - 排序： - 外层循环： - 内层双指针： - 总计：
空间复杂度：到（排序栈空间）

深入解读

算法原理：为什么这个算法能 work？

核心思想：将三数之和问题转化为两数之和。固定第一个数 nums[i] 后，问题变成：在 nums[i+1:] 中找到两个数，它们的和等于 -nums[i]。排序后可以使用对撞指针高效解决。

去重策略：必须在三个位置去重： 1. 第一个数：if i > 0 and nums[i] == nums[i-1]: continue 2. 第二个数：找到解后，跳过所有重复的 nums[left] 3. 第三个数：找到解后，跳过所有重复的 nums[right]

为什么需要三层去重： - 如果只去重第一个数：[-1,-1,0,1] 可能产生 [-1,0,1] 两次 - 如果不去重第二、三个数：[-2,0,0,2] 可能产生 [-2,0,2] 两次

时间复杂度证明：为什么是 O(n ²)？

排序：
外层循环：固定第一个数，次迭代
内层双指针：每次迭代最多次操作
总时间： 优化效果：相比暴力法，优化到，提升显著。

空间优化：有没有更省空间的方法？

方法一：原地排序 - 使用原地排序算法：栈空间 - 已经是最优

方法二：不排序（哈希表） - 使用哈希表存储两数之和：时间，空间 - 时间相同但空间更大，不推荐

权衡：当前方法在时间和空间上都是最优的。

常见错误分析

错误类型	错误代码	问题	正确做法
去重位置错误	在 `if` 前跳过重复	可能跳过有效解	找到解后再跳过
忘记移动指针	找到解后不移动	无限循环	`left += 1; right -= 1`
早期终止条件错误	`if nums[i] >= 0`	可能错过负数解	`if nums[i] > 0`

变体扩展

四数之和：添加另一个外层循环，固定两个数
最接近的三数之和：找和最接近目标值的三元组
三数之和（ BST）：在二叉搜索树中查找

去重策略详解

去重点一：第一个数

1 2	if i > 0 and nums[i] == nums[i-1]: continue

示例：nums = [-1, -1, 0, 1, 2]

在，处理 nums[0] = -1
在，跳过（因为 nums[1] = nums[0] = -1）

去重点二和三：第二个和第三个数

while left < right and nums[left] == nums[left+1]:
    left += 1
while left < right and nums[right] == nums[right-1]:
    right -= 1

示例：nums = [-4, -1, -1, 0, 1, 2]，固定 nums[0] = -4

找到解 [-4, -1, 5] 后
left 跳过所有重复的 -1
right 跳过所有重复的 5（如果有）

优化技术

优化一：早期终止

1 2	if nums[i] > 0: break

原因：数组已排序，如果最小数 > 0，所有后续数都是正数，不可能和为 0

优化二：最大值剪枝

1 2	if nums[i] + nums[i+1] + nums[i+2] > 0: break

原因：当前三个最小数已经和 > 0，没有继续的必要

优化三：最小值剪枝

1 2	if nums[i] + nums[n-2] + nums[n-1] < 0: continue

原因：当前数与两个最大数的和仍然 < 0，跳过此次迭代

扩展：四数之和、 k 数之和

四数之和：添加另一个外层循环，固定两个数然后对剩余两个数使用双指针。时间复杂度： k 数之和（通用化）：

def kSum(nums, target, k):
    def helper(start, k, target):
        if k == 2:
            # 双指针基本情况
            left, right = start, len(nums) - 1
            while left < right:
                s = nums[left] + nums[right]
                if s < target:
                    left += 1
                elif s > target:
                    right -= 1
                else:
                    result.append(path + [nums[left], nums[right]])
                    left += 1
                    right -= 1
                    while left < right and nums[left] == nums[left-1]:
                        left += 1
        else:
            # 递归情况
            for i in range(start, len(nums) - k + 1):
                if i > start and nums[i] == nums[i-1]:
                    continue
                path.append(nums[i])
                helper(i + 1, k - 1, target - nums[i])
                path.pop()
  
    nums.sort()
    result = []
    path = []
    helper(0, k, target)
    return result

模式二：快慢指针

核心特征

快指针每次迭代移动多步（通常 2 步）
慢指针每次迭代移动较少步（通常 1 步）
用于环检测、找中点、特定位置

现实类比

两个跑步者在圆形跑道上：

快跑者： 2 米/秒
慢跑者： 1 米/秒
如果跑道是圆形的，快跑者最终会追上慢跑者
如果跑道有终点，快跑者会先到达终点

LeetCode 141: 环形链表

问题分析

核心难点：如何在空间内检测链表是否有环。使用哈希集合存储访问过的节点需要空间，不符合进阶要求。

解题思路：使用快慢指针（ Floyd 环检测算法，又称"龟兔赛跑"）。慢指针每次移动 1 步，快指针每次移动 2 步。如果链表有环，快指针最终会追上慢指针（在环内相遇）；如果没有环，快指针会先到达链表末尾（None）。这个算法的正确性基于数学原理：如果存在环，快指针和慢指针的速度差会保证它们最终相遇。

复杂度分析： - 时间复杂度： - 无环时快指针需要步到达末尾；有环时快指针在 $ n $次迭代内追上慢指针空间复杂度：$ O(1)$ - 仅使用两个指针

关键洞察：快慢指针的速度差（ 2:1）保证了在有环的情况下，快指针会"追上"慢指针。这是经典的"追及问题"在链表中的应用。

问题描述

给你一个链表的头节点 head，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。

进阶：你能用空间解决吗？

示例：

输入：head = [3,2,0,-4]，尾节点连接到索引 1 的节点
输出：true

核心洞察： Floyd 环检测算法

龟兔赛跑：

慢指针（乌龟）每次迭代移动 1 步
快指针（兔子）每次迭代移动 2 步
如果存在环，快指针最终会追上慢指针
如果没有环，快指针会到达链表末尾

Python 实现

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def hasCycle(head):
    # 边界情况：空链表或单节点链表不可能有环
    if not head or not head.next:
        return False
  
    # 初始化快慢指针
    # 慢指针：每次移动 1 步
    slow = head
    # 快指针：每次移动 2 步（从 head.next 开始，确保初始位置不同）
    fast = head.next
  
    # 循环直到两指针相遇或快指针到达末尾
    while slow != fast:
        # 检查快指针是否到达末尾（无环的情况）
        # 需要检查 fast 和 fast.next，因为 fast 移动 2 步
        if not fast or not fast.next:
            return False  # 无环
        
        # 移动指针
        slow = slow.next        # 慢指针移动 1 步
        fast = fast.next.next   # 快指针移动 2 步
  
    # 如果循环退出是因为 slow == fast，说明有环
    return True

替代实现（都从头开始）

def hasCycle_v2(head):
    slow = fast = head
  
    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next
        if slow == fast:
            return True
  
    return False

复杂度分析

时间复杂度： - 无环：快指针需要步到达末尾
- 有环：快指针在次迭代内追上慢指针
空间复杂度：，仅使用两个指针

算法过程可视化：下面的动画演示了快慢指针如何检测环的完整过程：

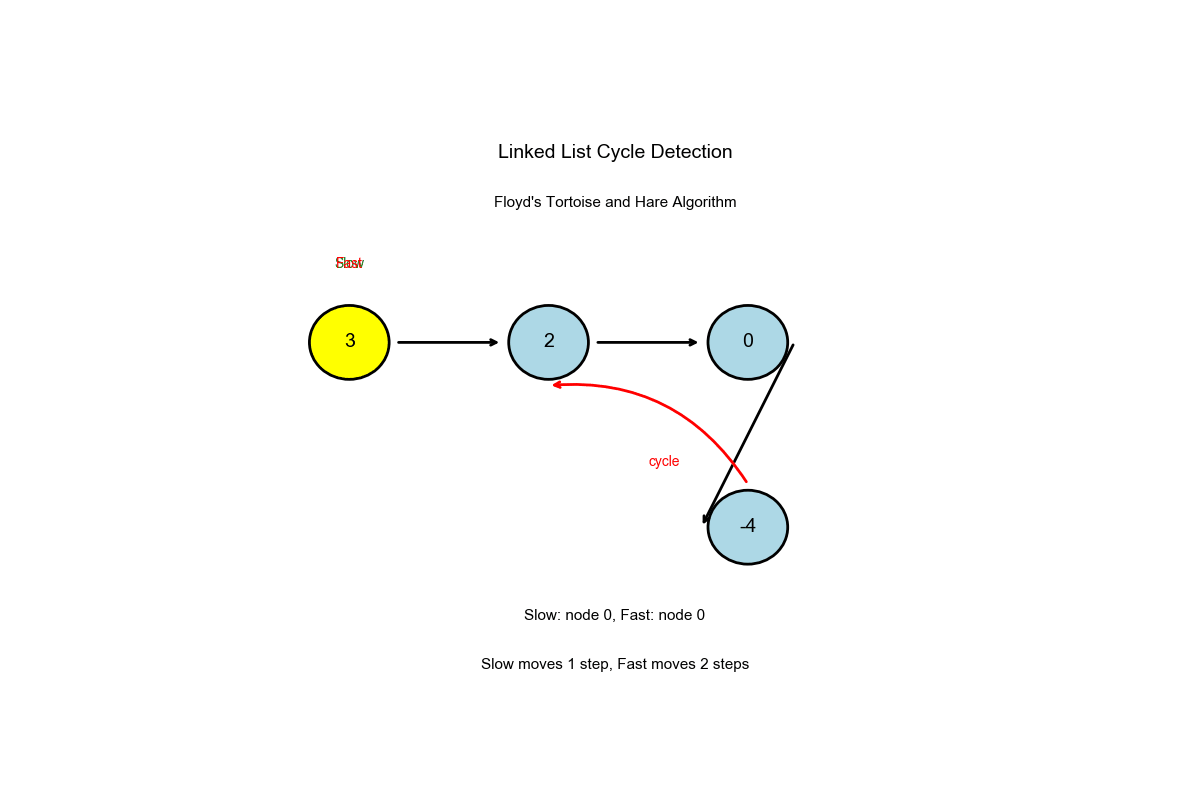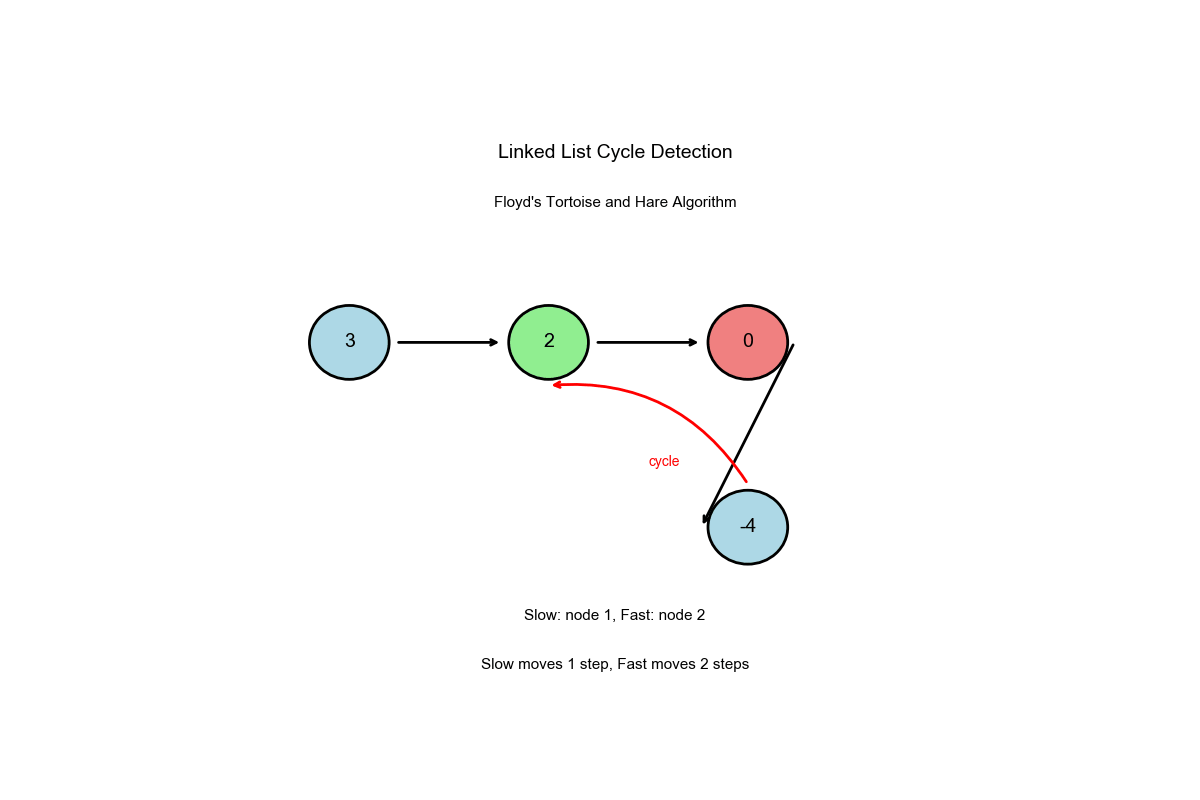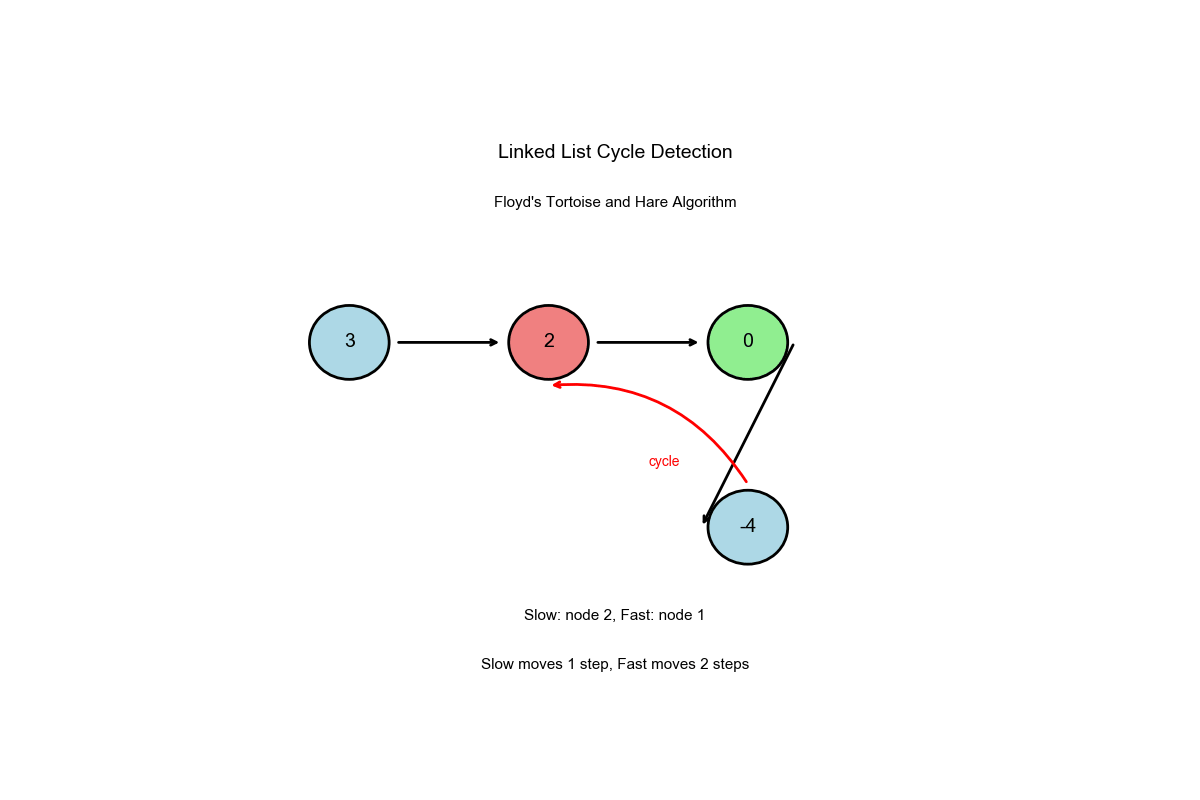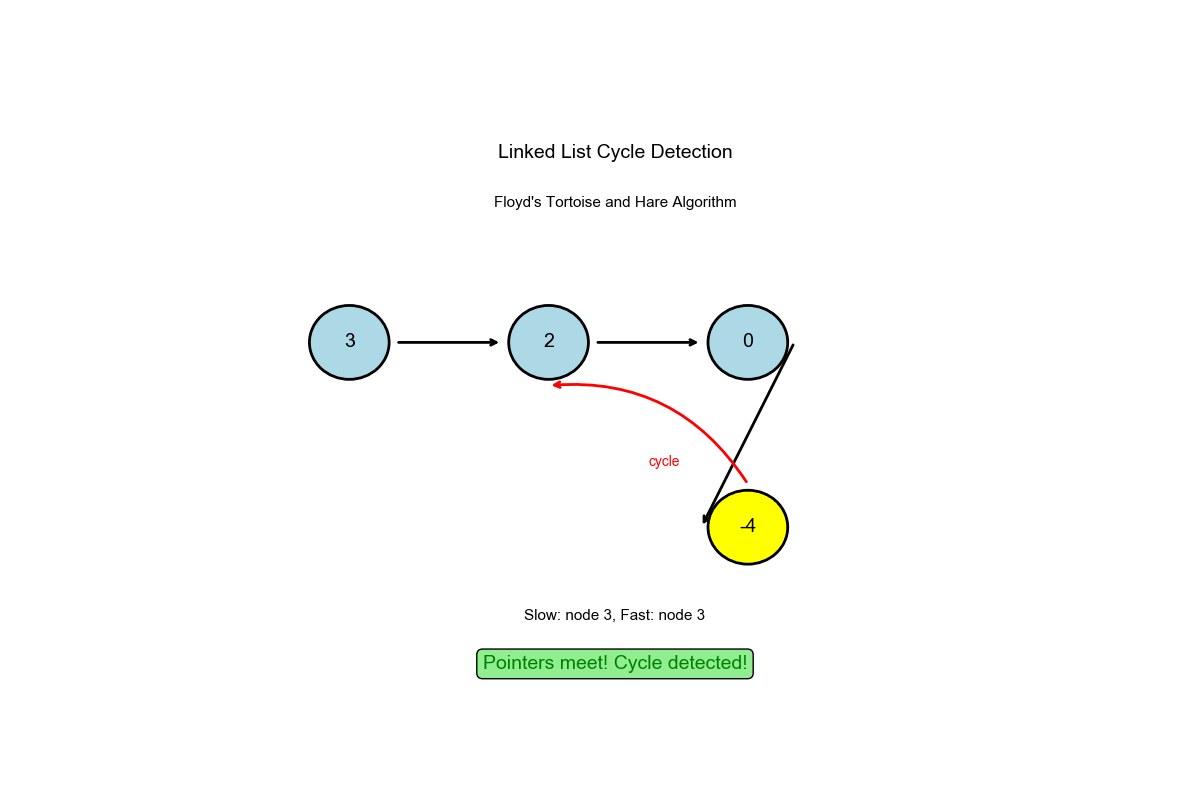
深入解读

算法原理：为什么快指针总是能追上慢指针？

数学证明：假设环长度为，慢指针进入环后移动了步。快指针落后慢指针步（）。 - 每次迭代，快指针缩小差距 1 步（快指针移动 2 步，慢指针移动 1 步） - 距离从变为 - 最多次迭代后，距离变为 0（它们相遇）

可视化：想象时钟指针——分针（快）最终会追上时针（慢）。

时间复杂度证明：为什么是 O(n)？

无环情况： - 快指针移动速度是慢指针的 2 倍 - 快指针需要 $ n/2 $步到达末尾时间复杂度：$ O(n)$ 有环情况： - 设环长度为，链表长度为 - 慢指针最多移动步进入环 - 进入环后，快指针最多需要步追上慢指针 - 总时间：（因为）

空间优化：有没有更省空间的方法？

这个问题已经是空间最优的： - 快慢指针：空间 - 哈希集合方法：空间（存储访问过的节点） - 无法进一步优化：必须跟踪指针位置

对比： | 方法 | 时间 | 空间 | 优势 | |------|------|------|------| | 快慢指针 | | | 空间最优 | | 哈希集合 | | | 代码更简单 |

常见错误分析

错误类型	错误代码	问题	正确做法
初始位置相同	`slow = fast = head`	初始就相等，可能误判	错开初始位置
忘记检查 fast.next	`if not fast`	可能访问 `None.next`	`if not fast or not fast.next`
移动顺序错误	先移动再检查	可能越界	先检查再移动

变体扩展

环形链表 II：找到环的入口节点
快乐数：使用快慢指针检测循环
链表中间节点：快指针到达末尾时，慢指针在中点

为什么快指针总是能追上慢指针？

数学证明：

假设环长度为，慢指针进入环后移动了步。快指针落后慢指针步（）。

每次迭代，快指针缩小差距 1 步
距离从变为
最多次迭代后，距离变为 0（它们相遇）

可视化：想象时钟指针——分针（快）最终会追上时针（慢）。

进阶：找到环的入口点

问题：返回环开始的节点。

算法：

使用快慢指针找到相遇点
将一个指针移回头部
两个指针以相同速度移动，它们会在环入口相遇

def detectCycle(head):
    if not head or not head.next:
        return None
  
    # 阶段一：检测环
    slow = fast = head
    has_cycle = False
  
    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next
        if slow == fast:
            has_cycle = True
            break
  
    if not has_cycle:
        return None
  
    # 阶段二：找到入口点
    slow = head
    while slow != fast:
        slow = slow.next
        fast = fast.next
  
    return slow

为什么这样可行？

设：

从头部到环入口的距离：
从环入口到相遇点的距离：
从相遇点回到环入口的距离：当它们相遇时：
慢指针移动了：
快指针移动了：因为快指针是慢指针的 2 倍：

a = c $$

所以从头部和相遇点开始，以相同速度移动，它们会在入口相遇！

LeetCode 202: 快乐数

问题描述

编写一个算法来判断一个数是不是"快乐数"。

一个"快乐数"定义为：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和，然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1 。如果可以变为 1，那么这个数就是快乐数。

示例：

输入：n = 19
输出：true
解释：
- - - -

核心洞察

关键观察：如果不是快乐数，数字会进入循环。

转换为环检测：

使用快慢指针检测环
如果快指针到达 1，它是快乐数
如果快指针和慢指针相遇（不在 1），它不是快乐数

Python 实现

def getNext(n):
    """计算数字各位的平方和"""
    total = 0
    while n > 0:
        digit = n % 10
        total += digit ** 2
        n //= 10
    return total

def isHappy(n):
    slow = n
    fast = getNext(n)
  
    while fast != 1 and slow != fast:
        slow = getNext(slow)          # 慢指针移动 1 步
        fast = getNext(getNext(fast))  # 快指针移动 2 步
  
    return fast == 1

复杂度分析

时间复杂度： - 每次操作大致减少数字大小（位数减少）
- 最坏情况进入循环，循环长度有界
空间复杂度：

算法过程可视化：下面的动画展示了快慢指针如何检测数字序列中的循环：

为什么不使用哈希集合？

哈希集合方法：

def isHappy_hash(n):
    seen = set()
    while n != 1 and n not in seen:
        seen.add(n)
        n = getNext(n)
    return n == 1

对比：

方法	时间复杂度	空间复杂度	优势
哈希集合			代码更简单
快慢指针			最优空间

面试提示：先提及哈希集合，然后提供快慢指针作为空间优化。

模式三：滑动窗口

核心特征

维护一个可变长度或固定长度的窗口
左指针和右指针定义窗口边界
动态调整窗口大小以满足条件

现实类比

阅读一本长书以找到包含所有关键情节点的最短连续章节：

右指针：不断向前翻页，扩大范围
左指针：一旦满足条件，从开头缩小
最终找到满足条件的最短章节序列

LeetCode 3: 无重复字符的最长子串

问题分析

核心难点：如何在时间内找到最长无重复字符的子串，而不是暴力检查所有个可能的子串。子串必须是连续的，这提示可以使用滑动窗口技术。

解题思路：使用滑动窗口（双指针）+ 哈希集合。右指针不断扩展窗口，将新字符加入集合；如果发现重复字符，左指针缩小窗口（从集合中移除字符）直到无重复。关键优化是使用哈希映射存储字符的最近索引，这样可以直接跳到重复字符之后，而不是逐个移动左指针。

复杂度分析： - 时间复杂度： - 每个字符最多访问两次（一次被右指针，一次被左指针） - 空间复杂度： - 是字符集大小（例如， ASCII 是 128）

关键洞察：滑动窗口的本质是维护一个满足条件的连续区间。当条件被违反时，通过移动左指针恢复条件；当条件满足时，通过移动右指针扩展区间。

问题描述

给定一个字符串 s，请你找出其中不含有重复字符的最长子串的长度。

示例：

输入：s = "abcabcbb"
输出：3
解释：最长子串是 "abc"

约束条件：

s 由英文字母、数字、符号和空格组成

核心洞察

滑动窗口 + 哈希集合：

使用哈希集合跟踪当前窗口中的字符
右指针扩大窗口，添加新字符
如果发现重复，左指针缩小窗口直到无重复
在整个过程中跟踪最大窗口长度

Python 实现

def lengthOfLongestSubstring(s):
    # 使用集合跟踪当前窗口中的字符（实现 O(1) 查找）
    char_set = set()
    left = 0  # 左指针：窗口左边界
    max_length = 0  # 记录最长子串长度
  
    # 右指针：不断扩展窗口
    for right in range(len(s)):
        # 如果右指针指向的字符已经在窗口中（重复）
        # 需要缩小左边界直到无重复
        while s[right] in char_set:
            # 从集合中移除左指针指向的字符
            char_set.remove(s[left])
            # 左指针右移，缩小窗口
            left += 1
    
        # 将当前字符添加到集合（窗口）
        char_set.add(s[right])
    
        # 更新最大长度
        # right - left + 1 是当前窗口的长度
        max_length = max(max_length, right - left + 1)
  
    return max_length

复杂度分析

时间复杂度： - 每个字符最多访问两次（一次被右指针，一次被左指针）
空间复杂度： - 是字符集大小（例如， ASCII 是 128）

深入解读

算法原理：为什么滑动窗口能 work？

核心思想：维护一个不包含重复字符的窗口 [left, right]。当窗口满足条件时，扩展右边界；当条件被违反（出现重复）时，收缩左边界直到条件恢复。

为什么每个字符最多访问两次： - 右指针访问：每个字符被右指针访问一次（扩展窗口） - 左指针访问：每个字符被左指针访问一次（收缩窗口） - 总操作数：

时间复杂度证明：为什么是 O(n)？

虽然代码中有嵌套的 while 循环，但： - 左指针单调递增：left 只能向右移动，不会回退 - 总移动次数：左指针最多移动 $ n $次右指针移动：$ n $次总时间：$ O(n)$ 关键：内层 while 循环不会重置 left 到 0，而是从当前位置继续移动。

空间优化：使用哈希映射直接跳转

优化版本：使用哈希映射存储字符的最近索引，可以直接跳到重复字符之后：

def lengthOfLongestSubstring_optimized(s):
    char_index = {}  # 字符 → 最近索引
    left = 0
    max_length = 0
  
    for right in range(len(s)):
        if s[right] in char_index:
            # 直接跳到重复字符之后
            # max() 防止左指针回退
            left = max(left, char_index[s[right]] + 1)
    
        char_index[s[right]] = right
        max_length = max(max_length, right - left + 1)
  
    return max_length

为什么需要 max(left, ...)：防止左指针回退。例如 s = "abba"： - 在 right = 3，遇到第二个 'a' - char_index['a'] = 0，但 left 已经在 2（由于第二个 'b'） - 需要 left = max(2, 1) = 2 避免回退

常见错误分析

错误类型	错误代码	问题	正确做法
使用列表而非集合	`char_list = []`	查找是	使用 `set()`
忘记更新最大长度	只扩展不记录	无法返回答案	`max_length = max(...)`
左指针回退	`left = char_index[c] + 1`	可能回退	`left = max(left, ...)`

变体扩展

最长重复字符替换：允许替换 k 个字符
最小窗口子串：找到包含目标字符串所有字符的最小子串
字符串的排列：检查是否包含目标字符串的排列

逐步示例

输入：s = "abcabcbb"

步骤	`right`	`s[right]`	`char_set`	窗口	`max_length`	操作
0	0	`'a'`	`{'a'}`	`"a"`	1	添加 `'a'`
1	1	`'b'`	`{'a','b'}`	`"ab"`	2	添加 `'b'`
2	2	`'c'`	`{'a','b','c'}`	`"abc"`	3	添加 `'c'`
3	3	`'a'`	`{'b','c'}`	`"bca"`	3	删除 `'a'`，添加 `'a'`
4	4	`'b'`	`{'c','a'}`	`"cab"`	3	删除 `'b'`，添加 `'b'`
5	5	`'c'`	`{'a','b'}`	`"abc"`	3	删除 `'c'`，添加 `'c'`
6	6	`'b'`	`{'a','c'}`	`"cb"`	3	删除 `'a'`，`'b'`，添加 `'b'`
7	7	`'b'`	`{'c'}`	`"b"`	3	删除 `'a'`，`'b'`，添加 `'b'`

输出：3

优化：带索引的哈希映射

进一步优化：不是逐个删除字符，而是直接跳到重复位置之后。

def lengthOfLongestSubstring_optimized(s):
    char_index = {}  # 字符 → 最近索引
    left = 0
    max_length = 0
  
    for right in range(len(s)):
        if s[right] in char_index:
            # 跳到重复位置之后
            left = max(left, char_index[s[right]] + 1)
    
        char_index[s[right]] = right
        max_length = max(max_length, right - left + 1)
  
    return max_length

为什么 max(left, ...)？

防止左指针向后移动。示例：s = "abba"

在 right = 3，遇到第二个 'a'
char_index['a'] = 0，天真地会设置 left = 1
但 left 可能已经在 2（由于第二个 'b'）
所以需要 left = max(left, 1) 以避免回退

LeetCode 76: 最小窗口子串

问题分析

核心难点：这道题的关键挑战在于如何在时间内找到包含目标字符串所有字符的最小子串。需要同时满足"包含所有字符"和"最小长度"两个条件，这要求精确控制窗口的扩展和收缩。

解题思路：使用滑动窗口 + 频率统计。使用哈希映射统计 t 中每个字符的频率作为目标，维护当前窗口的字符频率。关键技巧是使用 formed 变量跟踪窗口中满足目标频率的字符数量，只有当 formed == required 时才尝试缩小窗口。这样确保窗口始终包含所有必需字符，同时通过收缩找到最小窗口。

复杂度分析： - 时间复杂度： - $ m = $，$ n = $，每个字符最多访问两次空间复杂度：$ O(m + n)$ - 哈希映射存储字符频率

关键洞察：滑动窗口的收缩条件不是"窗口大小"，而是"是否包含所有必需字符"。只有当窗口满足条件时，才尝试收缩以优化长度。

问题描述

给你一个字符串 s、一个字符串 t。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 ""。

示例：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

约束条件：

s 和 t 由英文字母组成
进阶：时间复杂度

核心洞察

滑动窗口 + 频率统计：

使用哈希映射统计 t 中每个字符的频率
扩大右边界，将字符添加到窗口
当窗口包含所有必需字符时，缩小左边界以找到最小值
跟踪最小窗口的起始位置和长度

Python 实现

from collections import Counter, defaultdict

def minWindow(s, t):
    # 边界情况处理
    if not s or not t:
        return ""
  
    # 统计 t 中每个字符的频率（目标频率）
    target_count = Counter(t)
    # required：需要满足频率要求的唯一字符数量
    # 例如 t="AAB"，需要满足 'A':2, 'B':1， required=2
    required = len(target_count)  # 需要的唯一字符数
  
    # 当前窗口中的字符频率统计
    window_count = defaultdict(int)
    # formed：窗口中已经满足目标频率的字符数量
    # 当 formed == required 时，窗口包含所有必需字符
    formed = 0  # 窗口中具有所需频率的唯一字符数
  
    left = 0  # 左指针：窗口左边界
    min_len = float('inf')  # 最小窗口长度
    min_left = 0  # 最小窗口的起始位置
  
    # 右指针：不断扩展窗口
    for right in range(len(s)):
        char = s[right]
        # 将右指针指向的字符加入窗口
        window_count[char] += 1
    
        # 检查当前字符是否满足目标频率要求
        # 只有当频率恰好等于目标频率时， formed 才增加
        # 如果频率超过目标， formed 不增加（已经满足）
        if char in target_count and window_count[char] == target_count[char]:
            formed += 1
    
        # 当窗口包含所有必需字符时，尝试缩小窗口
        # 使用 while 而不是 if，因为可能可以多次缩小
        while left <= right and formed == required:
            # 更新最小窗口（如果当前窗口更小）
            if right - left + 1 < min_len:
                min_len = right - left + 1
                min_left = left  # 记录起始位置
        
            # 移除左指针指向的字符（缩小窗口）
            char = s[left]
            window_count[char] -= 1
            
            # 如果移除后，该字符的频率低于目标频率
            # formed 减 1，窗口不再满足条件
            if char in target_count and window_count[char] < target_count[char]:
                formed -= 1
        
            # 左指针右移，缩小窗口
            left += 1
  
    # 如果找到了最小窗口，返回子串；否则返回空字符串
    return "" if min_len == float('inf') else s[min_left:min_left + min_len]

复杂度分析

时间复杂度： - ， - 每个字符最多访问两次
空间复杂度： - 哈希映射存储字符频率

深入解读

算法原理：为什么这个算法能 work？

核心思想：维护一个包含所有必需字符的窗口。使用 formed 变量跟踪窗口中满足目标频率的字符数量，只有当 formed == required 时，窗口才包含所有必需字符。

为什么使用 formed 而不是直接比较频率映射： - 直接比较两个频率映射需要时间（是字符集大小） - 使用 formed 计数器，每次更新是 - 总时间从优化到 收缩条件：只有当 formed == required 时才收缩，确保窗口始终包含所有必需字符。

时间复杂度证明：为什么是 O(m+n)？

构建目标频率映射：遍历 t，
主循环：遍历 s，
内层 while：虽然嵌套，但每个字符最多被左指针访问一次
总时间：关键：左指针单调递增，不会回退，保证了线性时间复杂度。

算法过程可视化：下面的动画演示了滑动窗口如何动态调整大小以找到最小覆盖子串：

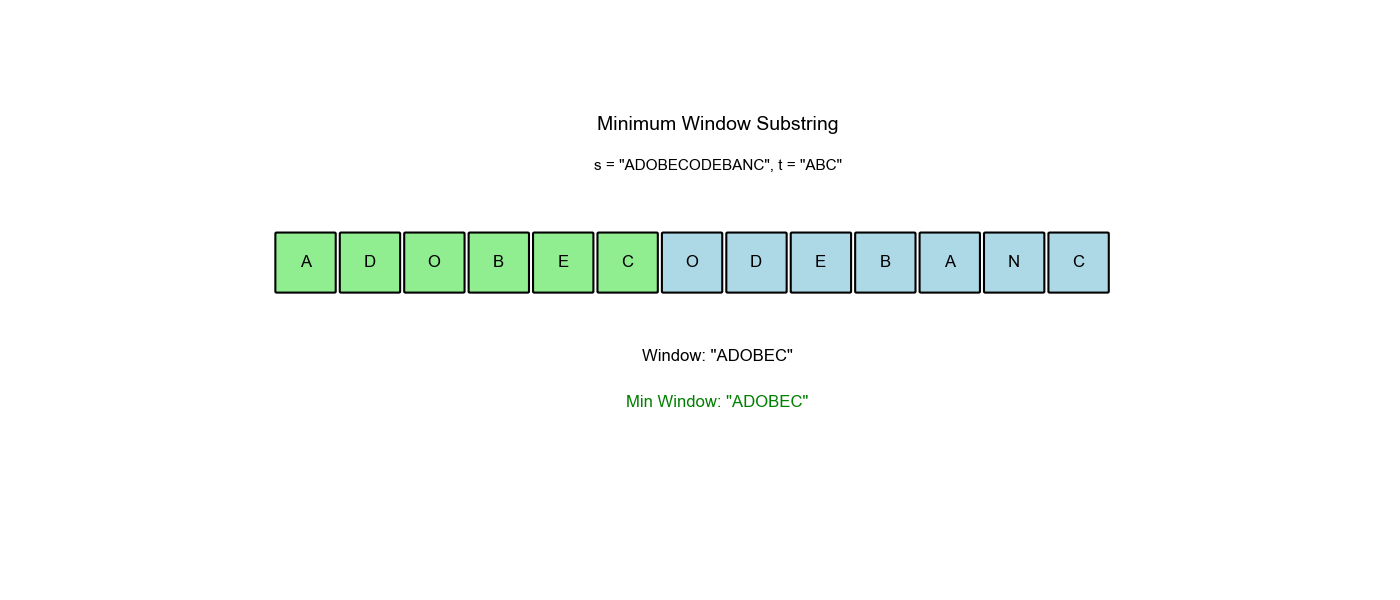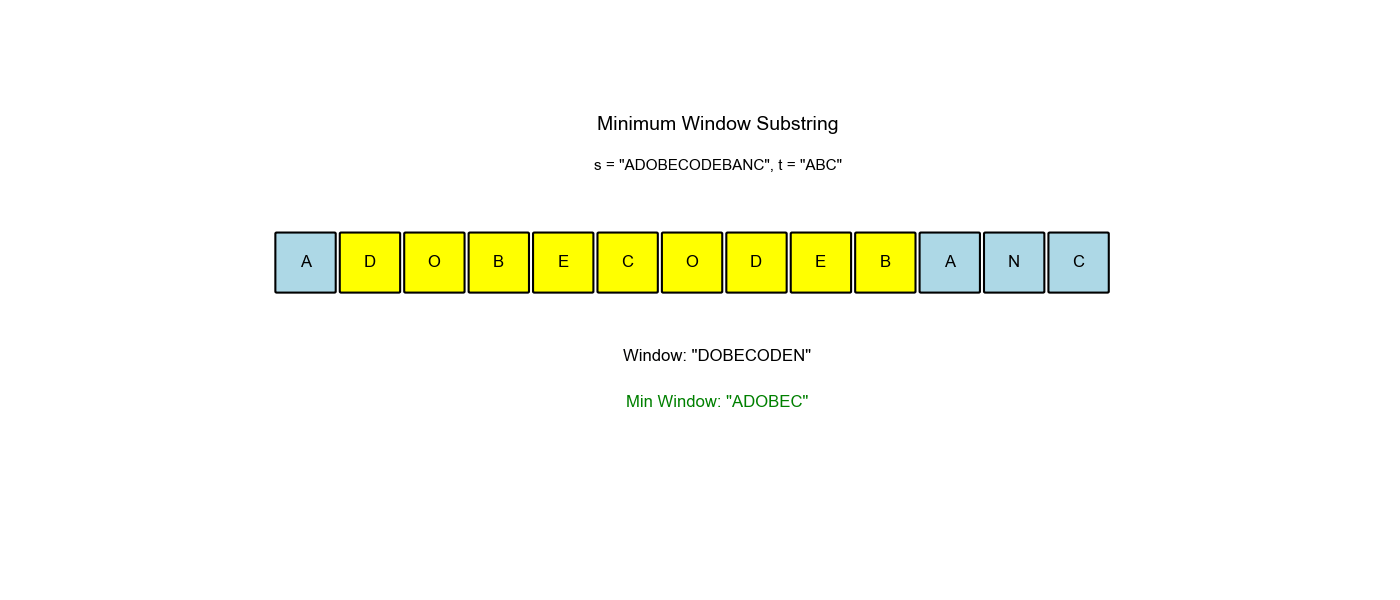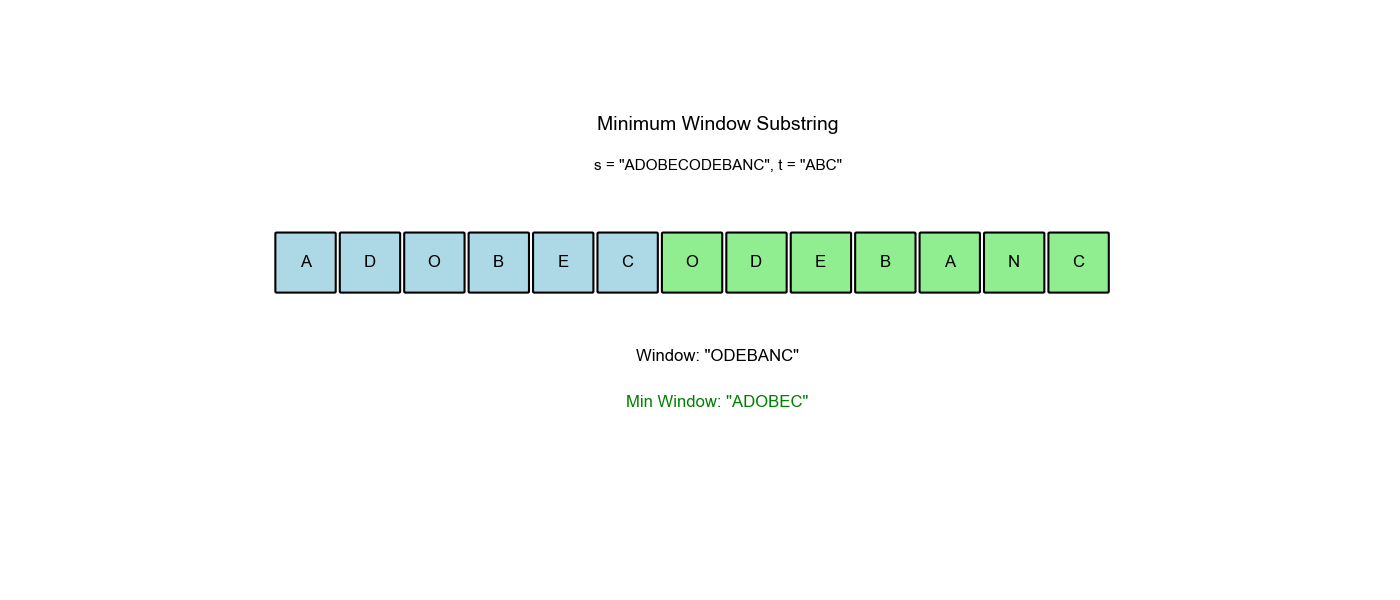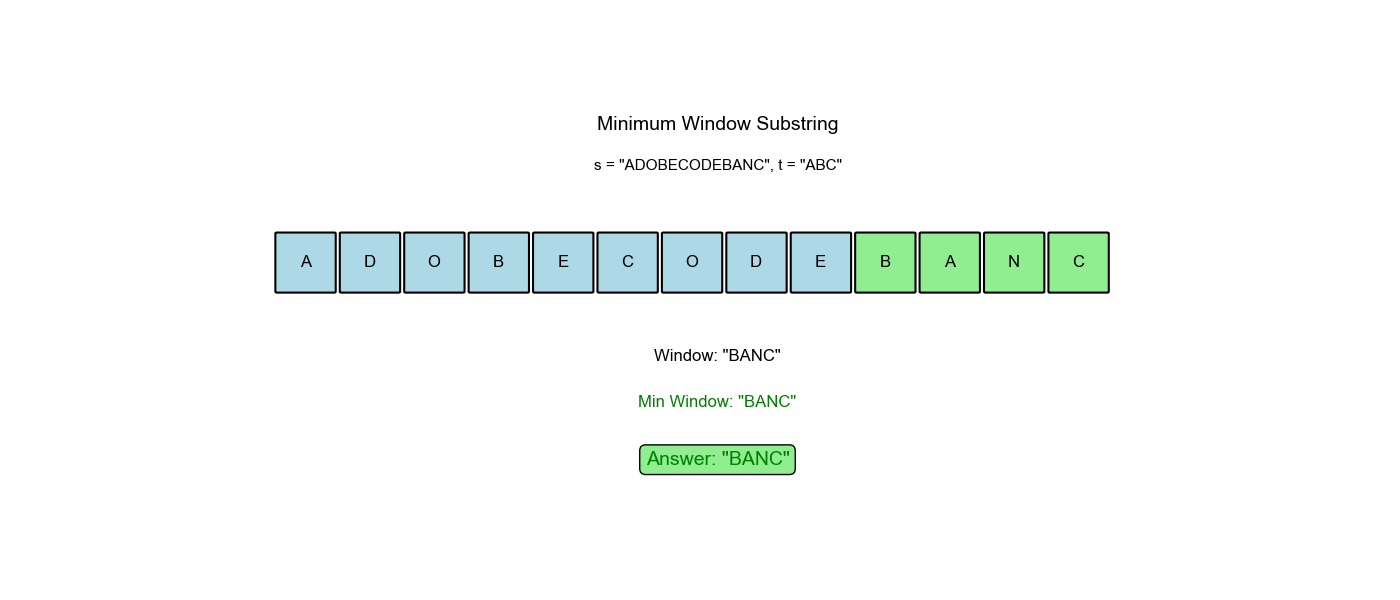
空间优化：有没有更省空间的方法？

方法一：使用数组代替字典（仅适用于小字符集） 对于小写英文字母（ 26 个），可以使用数组：

target_count = [0] * 26
for c in t:
    target_count[ord(c) - ord('a')] += 1
# 空间： O(1) 而不是 O(n)

方法二：复用变量 - 可以复用 char 变量，但空间节省微乎其微

权衡：对于一般字符集，使用 Counter 和 defaultdict 是合理的。

常见错误分析

错误类型	错误代码	问题	正确做法
formed 更新错误	`if char in target_count: formed += 1`	频率可能超过目标	检查 `==` 而非 `>=`
使用 if 而非 while	`if formed == required: left += 1`	只缩小一次，可能不是最小	使用 `while` 持续缩小
忘记记录起始位置	只记录长度	无法返回子串	同时记录 `min_left`

变体扩展

字符串的排列：找到包含目标字符串排列的最短子串
找到字符串中所有字母异位词：找到所有满足条件的子串起始位置
最小窗口子序列：子序列而非子串（更复杂）

关键实现细节

细节一：何时递增 `formed`

# ❌ 错误：仅检查存在
if char in target_count:
    formed += 1

# ✅ 正确：检查频率匹配
if char in target_count and window_count[char] == target_count[char]:
    formed += 1

细节二：缩小条件

# ❌ 错误：仅缩小一次
if formed == required:
    left += 1

# ✅ 正确：在条件满足时持续缩小
while left <= right and formed == required:
    # ...
    left += 1

细节三：更新最小值

# 跟踪起始位置和长度
min_len = right - left + 1
min_left = left

# 最终答案
s[min_left:min_left + min_len]

双指针 vs 哈希表：何时选择？

对比表

维度	双指针	哈希表
时间复杂度	或
空间复杂度
适用场景	排序数组、链表、子数组	未排序数组、频率统计
代码复杂度	更多边界条件	相对简单
需要排序	通常是	否

选择指南

优先使用双指针当

数组已排序或可以排序
需要原地操作（空间）
问题涉及连续子数组/子串
需要找到特定元素对（不仅仅是存在检查）

优先使用哈希表当

数组未排序且不能排序（需要保留索引）
需要快速查找值是否存在
频率统计问题
空间不是限制因素

混合方法

某些问题受益于结合两种技术：

示例：滑动窗口（双指针）+ 哈希表（频率统计）

最小窗口子串
字符串的排列
找到字符串中所有字母异位词

面试沟通技巧

模板一：识别双指针机会

"我注意到这个问题涉及排序数组/子数组/配对，这提示使用双指针。我将使用左右/快慢指针，采用[特定移动策略]来优化暴力解法。"

模板二：解释移动逻辑

"当条件 A 成立时，我移动左指针以缩小窗口/减少值；当条件 B 成立时，我移动右指针以扩大窗口/增加值。这确保每个元素最多访问常数次，实现复杂度。"

模板三：处理边界情况

"我需要检查几个边界情况：空数组、单个元素、所有元素相同。对于边界条件，我将确保指针不越界并正确处理它们相遇时的逻辑。"

模板四：优化解释

"暴力解法是；双指针优化到。虽然排序增加复杂度到，但对于大数据集这仍然是显著改进。空间复杂度是（不包括排序栈空间），优于哈希表的。"

常见错误与调试清单

错误一：指针越界

# ❌ 可能越界
while left < len(nums) and right < len(nums):
    # ...
    right += 1

# ✅ 检查 right + 1
while left < right and right + 1 < len(nums):

错误二：无限循环

# ❌ 忘记移动指针
while left < right:
    if condition:
        # 处理逻辑
        pass  # 没有指针移动！

# ✅ 确保每个分支都移动指针
while left < right:
    if condition:
        left += 1
    else:
        right -= 1

错误三：边界条件处理

# ❌ 指针相遇时处理不当
while left < right:
    # ...

# ✅ 根据问题决定 < 或 <=
while left <= right:  # 允许指针重叠
    # ...

调试清单

✅ 编码前：

确定模式（对撞/快慢/滑动窗口）
澄清每个指针的初始位置
定义移动和终止条件
考虑边界情况（空、单个元素、全部相同）

✅ 编码后：

用小示例手动模拟每一步
每次迭代打印指针位置和窗口内容
测试空输入、单个元素、边界值
检查指针相遇时的处理
验证复杂度符合预期

练习题目（ 10 道推荐）

对撞指针

两数之和 II - 输入有序数组（ LeetCode 167）简单
盛最多水的容器（ LeetCode 11）← 已覆盖中等
三数之和（ LeetCode 15）← 已覆盖中等

快慢指针

环形链表（ LeetCode 141）← 已覆盖简单
环形链表 II（ LeetCode 142）中等
快乐数（ LeetCode 202）← 已覆盖简单

滑动窗口

无重复字符的最长子串（ LeetCode 3）← 已覆盖中等
最小窗口子串（ LeetCode 76）← 已覆盖困难
长度最小的子数组（ LeetCode 209）中等
字符串的排列（ LeetCode 567）中等

总结：一页纸掌握双指针

三种模式快速参考

模式	记忆口诀	典型问题
对撞指针	从两端挤压，调整和/差	盛水容器、三数之和
快慢指针	速度差，检测环	链表环、快乐数
滑动窗口	扩大右缩小左，动态区间	最长子串、最小窗口

何时使用？

看到这些关键词时考虑双指针：

"排序数组"
"连续子数组/子串"
"配对/三元组"
"链表环/中点"
"空间"

常见陷阱

指针越界：总是检查 right + 1 < len
无限循环：每个分支必须移动指针
边界混淆：< vs <=，取决于问题
重复元素：排序后跳过重复

面试黄金短语

"这个问题的暴力解法是，但我注意到[排序/子数组/配对]特征，这提示[对撞/快慢/滑动窗口]双指针可以优化到，空间复杂度为。这是时间和空间的最佳平衡。"

记忆口诀

对撞挤压调整和差，快慢追赶检测环，滑动窗口扩大缩小寻找区间，双指针巧妙节省空间！

下一步是什么？

在LeetCode（三）链表操作中，我们将深入探讨：

反转链表：迭代 vs 递归
合并列表：应用归并排序思维
列表排序：时间空间
快慢指针进阶：找中点、倒数第 k 个

思考题：如何在空间中对链表执行归并排序？下一部分见答案！

❓ Q&A：双指针常见问题

Q1：快慢指针 vs 对撞指针——什么时候使用每种？

答案：选择取决于问题结构和你要实现的目标。

快慢指针（不同速度）：

使用时机：处理链表、环检测、找中点，或需要跟踪相对位置的问题
关键洞察：速度差产生"追赶"效果，自然检测环或找到特定位置
示例：环形链表 - 快指针移动 2 步，慢指针移动 1 步。如果有环，快指针最终会追上慢指针。

# 快慢模式
slow = fast = head
while fast and fast.next:
    slow = slow.next      # 移动 1 步
    fast = fast.next.next # 移动 2 步
    if slow == fast:
        return True  # 检测到环

对撞指针（两端指针）：

使用时机：处理排序数组、找数对/三元组，或可以基于两端做决策的问题
关键洞察：从两端开始允许你通过每次比较消除一半搜索空间
示例：两数之和 II - 如果和太小，左指针右移；如果太大，右指针左移。

# 对撞模式
left, right = 0, len(nums) - 1
while left < right:
    if nums[left] + nums[right] == target:
        return [left, right]
    elif nums[left] + nums[right] < target:
        left += 1  # 需要更大的和
    else:
        right -= 1  # 需要更小的和

决策树：

链表问题 → 快慢指针
排序数组 + 数对/三元组 → 对撞指针
需要找中点 → 快慢指针
需要优化和/差 → 对撞指针

复杂度：两者都实现时间和空间，但快慢指针对链表更直观，而对撞指针对数组更自然。

Q2：滑动窗口 vs 双指针——有什么区别？

答案：滑动窗口实际上是双指针的专门形式，针对连续子数组/子串问题进行了优化。

双指针（通用）：

指针可以独立移动或收敛
用于：配对、环检测、找特定位置
移动：通常基于比较移动（例如，和太小/太大）

滑动窗口：

维护指针之间的连续区间
用于：有约束的子数组/子串问题
移动：右指针扩大窗口，满足条件时左指针缩小
关键特征：窗口大小可以是固定的或可变的

可视化对比：

双指针（对撞）：
[1, 2, 3, 4, 5, 6]
 ↑              ↑
left          right
（向中心收敛）

滑动窗口：
[1, 2, 3, 4, 5, 6]
 ↑  ↑
left right
（窗口向右扩大，向左缩小）

何时使用滑动窗口：

关键词："子数组"、"子串"、"连续"、"窗口"
需要跟踪范围内的元素
问题要求满足条件的最小/最大长度

示例：无重复字符的最长子串

滑动窗口：维护唯一字符窗口
不是对撞指针：我们不是从两端收敛
不是快慢指针：两个指针都向前移动，只是速度不同

复杂度：滑动窗口通常实现时间，因为每个元素最多访问两次（每个指针一次）。

Q3：如何避免双指针算法中的无限循环？

答案：确保每个代码路径都移动至少一个指针，并且终止条件总是可达的。

常见原因：

忘记指针移动：

# ❌ 差：无限循环风险
while left < right:
    if nums[left] + nums[right] == target:
        # 找到解，但忘记移动指针！
        pass

# ✅ 好：总是移动指针
while left < right:
    if nums[left] + nums[right] == target:
        result.append([left, right])
        left += 1      # 必须移动！
        right -= 1     # 必须移动！
    elif nums[left] + nums[right] < target:
        left += 1
    else:
        right -= 1

终止条件永远不满足：

# ❌ 差：条件可能永远不为假
while True:
    if some_condition:
        break  # 但如果条件永远不为真怎么办？

# ✅ 好：显式终止
while left < right:  # 指针相遇时自然终止
    # ... 保证 left 或 right 移动的逻辑

指针移动方向错误：

# ❌ 差：指针相互靠近但逻辑阻止相遇
while left < right:
    if condition:
        left += 1
    else:
        left += 1  # 两个分支都移动同一指针！

# ✅ 好：至少一个指针总是向另一个移动
while left < right:
    if condition:
        left += 1   # 向右移动
    else:
        right -= 1  # 向左移动

调试清单：

✅ 每个 if/elif/else 分支移动至少一个指针
✅ 终止条件（left < right 或 left <= right）最终会为假
✅ 指针移动方向正确（收敛，不发散）
✅ 没有跳过指针更新的早期返回

捕获无限循环的测试用例：

空数组：[]
单个元素：[1]
所有元素相同：[2, 2, 2, 2]
指针立即相遇的边缘情况

Q4：双指针问题中的常见边界情况有哪些？

答案：边界情况通常涉及边界条件和特殊输入模式。总是系统地测试这些。

关键边界情况：

空数组：

def twoSum(nums, target):
    if not nums:  # ✅ 首先检查！
        return []
    left, right = 0, len(nums) - 1
    # ... 其余逻辑

单个元素：

# 对于对撞指针： left == right 立即
# 对于快慢指针： fast.next 可能立即为 None
def hasCycle(head):
    if not head or not head.next:  # ✅ 单节点不能有环
        return False

所有元素相同：

# 示例： nums = [2, 2, 2, 2], target = 4
# 需要正确处理重复
while left < right:
    if nums[left] + nums[right] == target:
        result.append([left, right])
        # ✅ 跳过重复
        while left < right and nums[left] == nums[left+1]:
            left += 1
        while left < right and nums[right] == nums[right-1]:
            right -= 1
        left += 1
        right -= 1

指针在边界相遇：

# 如果解在索引 [0, 1] 或 [n-2, n-1] 怎么办？
# 确保循环处理第一个和最后一个元素
while left < right:  # ✅ 允许 left=0, right=1
    # ... 逻辑

无有效解：

# 示例：排序数组，但没有数对和为 target
# 应该返回空结果，不崩溃
def twoSum(nums, target):
    left, right = 0, len(nums) - 1
    while left < right:
        # ... 逻辑
    return []  # ✅ 未找到解

有重复的数组（三数之和/四数之和）：

# 必须在三个级别跳过重复：
# 1. 第一个数
if i > 0 and nums[i] == nums[i-1]:
    continue
# 2. 第二个数（左指针）
while left < right and nums[left] == nums[left+1]:
    left += 1
# 3. 第三个数（右指针）
while left < right and nums[right] == nums[right-1]:
    right -= 1

边界情况测试模板：

test_cases = [
    [],                    # 空
    [1],                   # 单个元素
    [1, 1],                # 两个相同
    [1, 1, 1, 1],          # 全部相同
    [1, 2, 3, 4, 5],       # 正常情况
    [1, 2],                # 最小大小
    [1] * 10000,           # 大输入，全部相同
]

面试提示：总是在编码前提及边界情况："我需要处理空数组、单个元素和重复元素。让我先编码主要逻辑，然后添加这些检查。"

Q5：链表中的双指针 vs 数组中的双指针——关键区别？

答案：根本区别是随机访问 vs 顺序访问，这影响指针如何移动以及可能执行的操作。

数组（随机访问）：

可以跳转到任何索引：nums[i], nums[j]
指针是索引：left = 0, right = len(nums) - 1
可以向后移动：right -= 1
可以计算距离：right - left
典型模式：对撞指针、滑动窗口

# 数组：容易双向移动
left, right = 0, len(nums) - 1
while left < right:
    # 可以直接访问 nums[left] 和 nums[right]
    if nums[left] + nums[right] == target:
        return [left, right]
    left += 1   # 向前移动
    right -= 1  # 向后移动

链表（顺序访问）：

必须从头遍历：node = node.next
指针是节点引用：slow = head, fast = head
只能向前移动：node = node.next（单链表中没有 node.prev）
不容易计算距离（需要遍历）
典型模式：快慢指针、环检测

# 链表：只能向前移动
slow = fast = head
while fast and fast.next:
    slow = slow.next      # 必须跟随 .next
    fast = fast.next.next # 不能跳转到任意位置
    if slow == fast:
        return True

关键区别表：

方面	数组	链表
访问模式	随机（ O(1)）	顺序（ O(n)）
指针类型	整数索引	节点引用
移动	双向	仅向前（单链表）
距离计算	`right - left`	必须遍历
常见模式	对撞指针	快慢指针
边界检查	`left < len(nums)`	`node is not None`

数组更好时：

需要比较两端的元素
问题需要排序（数组更容易排序）
需要计算距离或索引

链表更好时：

问题涉及环（快慢自然检测）
需要找中点而不知道长度
动态大小（插入/删除）

混合方法示例：某些问题首先将链表转换为数组：

# 转换为数组，然后使用对撞指针
def isPalindrome(head):
    values = []
    while head:
        values.append(head.val)
        head = head.next
    # 现在使用数组双指针
    left, right = 0, len(values) - 1
    while left < right:
        if values[left] != values[right]:
            return False
        left += 1
        right -= 1
    return True

复杂度权衡：转换为数组使用额外空间，但使双指针逻辑更简单。有时为了代码清晰性值得这样做。

Q6：什么是三指针技术？

答案：三指针扩展双指针逻辑以处理三路分区或需要三个同时引用的问题。

常见用例：

荷兰国旗问题（三路分区）：

# 用三种颜色排序数组： 0（红）、 1（白）、 2（蓝）
def sortColors(nums):
    # 三个指针：
    # left: 0 的边界（ left 之前都是 0）
    # right: 2 的边界（ right 之后都是 2）
    # curr: 当前正在处理的元素
    left = curr = 0
    right = len(nums) - 1
  
    while curr <= right:
        if nums[curr] == 0:
            nums[left], nums[curr] = nums[curr], nums[left]
            left += 1
            curr += 1
        elif nums[curr] == 2:
            nums[curr], nums[right] = nums[right], nums[curr]
            right -= 1
            # 不要递增 curr！需要检查交换的元素
        else:  # nums[curr] == 1
            curr += 1

可视化：

初始：[2, 0, 2, 1, 1, 0]
      ↑  ↑           ↑
     left curr      right

之后：[0, 0, 1, 1, 2, 2]
          ↑  ↑
        left right
        （ curr 完成）

分区数组（基于枢轴）：

# 分区使得元素 < 枢轴在左，= 枢轴在中，> 枢轴在右
def partition(nums, pivot):
    left = curr = 0
    right = len(nums) - 1
  
    while curr <= right:
        if nums[curr] < pivot:
            nums[left], nums[curr] = nums[curr], nums[left]
            left += 1
            curr += 1
        elif nums[curr] > pivot:
            nums[curr], nums[right] = nums[right], nums[curr]
            right -= 1
        else:
            curr += 1

四数之和问题（嵌套双指针）：

# 固定两个数，然后对剩余两个使用双指针
def fourSum(nums, target):
    nums.sort()
    result = []
    n = len(nums)
  
    for i in range(n - 3):  # 第一个指针
        for j in range(i + 1, n - 2):  # 第二个指针
            left = j + 1    # 第三个指针
            right = n - 1   # 第四个指针
        
            while left < right:
                total = nums[i] + nums[j] + nums[left] + nums[right]
                if total == target:
                    result.append([nums[i], nums[j], nums[left], nums[right]])
                    # 跳过重复...
                elif total < target:
                    left += 1
                else:
                    right -= 1

关键洞察：三指针通常维护三个区域：

区域 1：已处理并正确放置的元素（left 之前）
区域 2：正在处理的元素（left 到 curr）
区域 3：已处理并正确放置的元素（right 之后）

复杂度：仍然是时间，空间——只是需要管理更多指针。

何时使用：

问题需要三路分区
需要同时跟踪三个边界
扩展双指针逻辑以处理三个元素（如三数之和 → 四数之和）

Q7：带排序的双指针——权衡是什么？

答案：排序使双指针技术成为可能，但增加了预处理成本。权衡通常值得空间优化。

权衡分析：

不排序（哈希表方法）：

# 两数之和 - 未排序数组
def twoSum(nums, target):
    seen = {}
    for i, num in enumerate(nums):
        complement = target - num
        if complement in seen:
            return [seen[complement], i]
        seen[num] = i

时间：
空间：用于哈希表
保留：原始索引

带排序（双指针）：

# 两数之和 II - 排序数组
def twoSum(nums, target):
    nums.sort()  # O(n log n)
    left, right = 0, len(nums) - 1
    while left < right:
        current_sum = nums[left] + nums[right]
        if current_sum == target:
            return [left, right]  # 但这些是排序后的新索引！
        elif current_sum < target:
            left += 1
        else:
            right -= 1

时间：用于排序 + 用于双指针 =
空间：额外（不包括排序栈空间）
丢失：原始索引（除非存储它们）

排序值得时：

✅ 使用排序 + 双指针当：

问题要求值，不是索引（如三数之和、四数之和）
空间受限（ vs 重要）
问题需要多次查询（排序一次，查询多次）
需要找到所有数对/三元组（哈希表变得复杂）

❌ 避免排序当：

问题需要原始索引（两数之和原始）
数组已排序（直接使用双指针！）
单次查询且空间不是问题（哈希表更简单）

混合方法（两全其美）：

# 排序前存储原始索引
def twoSumWithIndices(nums, target):
    indexed = [(nums[i], i) for i in range(len(nums))]
    indexed.sort(key=lambda x: x[0])  # 按值排序
  
    left, right = 0, len(indexed) - 1
    while left < right:
        current_sum = indexed[left][0] + indexed[right][0]
        if current_sum == target:
            return [indexed[left][1], indexed[right][1]]  # 原始索引！
        elif current_sum < target:
            left += 1
        else:
            right -= 1

时间：
空间：用于存储索引
好处：获得双指针效率 + 保留索引

复杂度对比：

方法	时间	空间	保留索引
哈希表			✅ 是
排序 + 双指针			❌ 否
排序 + 存储索引			✅ 是

面试沟通：

"我可以用哈希表在时间和空间中解决这个问题，这对时间是最优的。或者，我可以先排序然后使用双指针实现时间但空间。由于这个问题要求值而不是索引，我将选择排序 + 双指针以优化空间。"

Q8：如何用双指针优化空间复杂度？

答案：双指针通过使用仅指针变量而不是辅助数据结构自然实现空间。关键是避免哈希表、数组或递归栈。

空间优化技术：

用双指针替换哈希表：

# ❌ 哈希表： O(n) 空间
def hasDuplicate(nums):
    seen = set()  # O(n) 空间
    for num in nums:
        if num in seen:
            return True
        seen.add(num)
    return False

# ✅ 双指针（如果排序）： O(1) 空间
def hasDuplicate(nums):
    nums.sort()  # 原地， O(log n) 栈空间
    for i in range(len(nums) - 1):
        if nums[i] == nums[i+1]:  # 相邻比较
            return True
    return False

原地数组修改：

# 原地删除重复
def removeDuplicates(nums):
    if not nums:
        return 0
  
    # 双指针：写指针和读指针
    write = 0  # 写入下一个唯一元素的位置
    for read in range(1, len(nums)):
        if nums[read] != nums[write]:
            write += 1
            nums[write] = nums[read]  # 原地修改
    return write + 1

空间：（仅两个整数指针）
替代：创建新数组 → 空间

避免递归栈：

# ❌ 递归： O(n) 栈空间
def reverseList(head):
    if not head or not head.next:
        return head
    new_head = reverseList(head.next)  # 递归栈
    head.next.next = head
    head.next = None
    return new_head

# ✅ 迭代双指针： O(1) 空间
def reverseList(head):
    prev = None
    curr = head
    while curr:
        next_temp = curr.next
        curr.next = prev
        prev = curr
        curr = next_temp
    return prev

无哈希表的滑动窗口（可能时）：

# 对于有限字符集的问题，使用数组而不是哈希映射
def lengthOfLongestSubstring(s):
    # ASCII 有 128 个字符，所以 array[128] 是 O(1) 空间
    # vs 哈希映射是 O(min(n, 128)) 但有过载
    char_count = [0] * 128  # 固定大小， O(1) 空间
    left = 0
    max_len = 0
  
    for right in range(len(s)):
        char_count[ord(s[right])] += 1
    
        # 如果有重复，缩小窗口
        while char_count[ord(s[right])] > 1:
            char_count[ord(s[left])] -= 1
            left += 1
    
        max_len = max(max_len, right - left + 1)
  
    return max_len

空间复杂度分解：

技术	空间复杂度	备注
双指针（基本）		仅指针变量
双指针 + 排序		递归排序栈空间
双指针 + 哈希表		破坏空间优化
滑动窗口 + 数组		= 字符集大小（通常常数）
滑动窗口 + 哈希映射		= 字符集大小

空间重要时：

内存受限环境（嵌入式系统）
大数据集，其中额外空间不可行
面试优化（显示对权衡的理解）
问题陈述要求的原地算法

权衡意识：有时空间有代价：

排序要求：增加时间预处理
代码复杂度：双指针可能比哈希表更棘手
索引保留：可能丢失原始位置

面试提示：总是提及两种方法：

"我可以用哈希表在时间和空间中解决这个问题，或者排序后使用双指针实现时间但空间。给定约束[提及哪个]，我将选择[方法]。"

Q9：双指针问题的面试沟通技巧

答案：有效沟通展示问题解决过程和权衡意识。清晰地构建你的解释。

模板一：问题识别：

"我注意到这个问题涉及[排序数组 / 子数组 / 环检测]，这提示双指针可以优化暴力解法。让我思考哪种模式最适合..."

模板二：模式选择：

"给定[数组已排序 / 需要连续子数组 / 我们处理链表]，我将使用[对撞指针 / 滑动窗口 / 快慢指针]，因为[特定原因]。"

模板三：算法解释：

"我将维护两个指针：[left/right 或 slow/fast]。[left/slow] 指针将[特定移动]，[right/fast] 指针将[特定移动]。当[条件]时，我将[操作]，这确保[不变量/保持正确性]。"

模板四：复杂度分析：

"时间复杂度是，因为每个元素最多访问[一次/两次]。空间复杂度是，因为我们只使用[数字]个指针变量，相比哈希表方法需要空间。"

模板五：边界情况：

"编码前，我应该处理：[1] 空输入，[2] 单个元素，[3] 所有元素相同，[4] 无有效解。让我先编码主要逻辑，然后添加这些检查。"

模板六：优化讨论：

"暴力解法将是，通过检查所有数对。双指针通过[消除一半搜索空间 / 每个元素访问一次]将其减少到。虽然需要先排序（），但对于大输入这仍然优于。"

常用短语：

"我将使用贪心方法，其中..."
"这维护不变量，即..."
"每次迭代消除[部分]剩余可能性..."
"关键洞察是可以基于[比较]进行[决策]..."

面试官想听到的：

✅ 良好沟通：

解释为什么你选择双指针
提及替代方案（哈希表、暴力）
讨论权衡（时间 vs 空间）
主动识别边界情况
逐步说明示例

❌ 差沟通：

直接跳到代码而不解释
不提及替代方案
忽略边界情况直到被问
无法解释为什么算法正确
不分析复杂度

完整解释示例：

"这是一个经典的双指针问题。暴力解法将检查所有数对，时间复杂度。由于数组已排序，我可以使用从两端开始的对撞指针。如果和太小，我移动左指针向右以增加它。如果太大，我移动右指针向左以减少它。这通过每次比较消除一半剩余数对，给出时间。空间是，因为我们只使用两个指针。要考虑的边界情况：空数组、单个元素和无有效解。让我编码这个..."

肢体语言提示：

大声思考：不要沉默编码
画图：可视化指针移动
询问澄清问题："我应该处理重复吗？" "你想要索引还是值？"
用示例测试：手动遍历小输入

避免的红旗：

❌ "我将只使用双指针"（太模糊）
❌ 不解释就编码（面试官无法跟随）
❌ 忽略后续问题
❌ 不测试边界情况

Q10：如何调试双指针算法？

答案：系统调试涉及手动追踪、打印语句和系统测试用例。大多数错误来自边界条件或指针移动逻辑。

调试策略：

手动逐步追踪：

# 示例：两数之和
nums = [2, 7, 11, 15], target = 9

# 追踪每次迭代：
# 迭代 1： left=0, right=3
#   nums[0] + nums[3] = 2 + 15 = 17 > 9
#   → 移动 right： right = 2
# 迭代 2： left=0, right=2
#   nums[0] + nums[2] = 2 + 11 = 13 > 9
#   → 移动 right： right = 1
# 迭代 3： left=0, right=1
#   nums[0] + nums[1] = 2 + 7 = 9 == target
#   → 返回 [0, 1] ✓

添加打印语句：

def twoSum(nums, target):
    left, right = 0, len(nums) - 1
    while left < right:
        current_sum = nums[left] + nums[right]
        print(f"left={left}, right={right}, sum={current_sum}")  # 调试
    
        if current_sum == target:
            return [left, right]
        elif current_sum < target:
            left += 1
            print(f"Moving left to {left}")  # 调试
        else:
            right -= 1
            print(f"Moving right to {right}")  # 调试

检查不变量：

# 什么应该总是为真？
def maxArea(height):
    left, right = 0, len(height) - 1
    max_area = 0
  
    while left < right:
        # 不变量： left < right（检查这个！）
        assert left < right, f"Invariant violated: left={left}, right={right}"
    
        width = right - left
        current_area = min(height[left], height[right]) * width
        max_area = max(max_area, current_area)
    
        if height[left] < height[right]:
            left += 1
        else:
            right -= 1
  
    return max_area

系统测试边界情况：

def test_twoSum():
    test_cases = [
        ([], 5, []),                    # 空
        ([1], 1, []),                   # 单个元素
        ([1, 2], 3, [0, 1]),            # 两个元素
        ([1, 1, 1], 2, [0, 1]),         # 全部相同
        ([1, 2, 3, 4], 10, []),         # 无解
        ([1, 2, 3, 4], 7, [2, 3]),      # 正常情况
    ]
  
    for nums, target, expected in test_cases:
        result = twoSum(nums, target)
        assert result == expected, f"Failed: {nums}, target={target}"
        print(f"✓ Passed: {nums}")

常见错误和修复：

错误一：差一错误：

# ❌ 差：可能跳过最后一个元素
for i in range(len(nums) - 1):
    if nums[i] + nums[i+1] == target:
        return [i, i+1]

# ✅ 好：检查边界
for i in range(len(nums)):
    if i + 1 < len(nums) and nums[i] + nums[i+1] == target:
        return [i, i+1]

错误二：指针不移动：

# ❌ 差：无限循环
while left < right:
    if nums[left] + nums[right] == target:
        # 忘记移动指针！
        pass

# ✅ 好：总是移动
while left < right:
    if nums[left] + nums[right] == target:
        return [left, right]
    elif nums[left] + nums[right] < target:
        left += 1
    else:
        right -= 1

错误三：错误比较：

# ❌ 差：移动错误指针
if nums[left] + nums[right] < target:
    right -= 1  # 错误！应该移动 left

# ✅ 好：移动增加和的指针
if nums[left] + nums[right] < target:
    left += 1  # 增加和

调试清单：

每次迭代打印指针值
检查终止条件最终会为假
验证指针移动方向正确
测试空输入、单个元素、边界情况
手动追踪小示例
访问前检查数组边界
验证不变量在整个循环中保持

面试调试提示：

不要恐慌：错误是正常的，展示调试过程
解释你的思考："我认为问题可能是..."
增量测试：一次添加一个测试用例
使用示例：遍历具体输入
检查假设："我假设数组已排序，这是正确的吗？"

双指针不是花哨的技巧——它是对数据结构属性的深入理解。掌握它，你将在线性时间内解决许多看似复杂的问题！

本文标题：LeetCode（二）—— 双指针技巧
本文作者：Chen Kai
创建时间：2020-01-11 14:00:00
本文链接：https://www.chenk.top/LeetCode%EF%BC%88%E4%BA%8C%EF%BC%89%E2%80%94%E2%80%94-%E5%8F%8C%E6%8C%87%E9%92%88%E6%8A%80%E5%B7%A7/
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！