贪心算法（ Greedy Algorithm）是一种在每一步选择中都采取当前状态下最优选择的算法思想。虽然看似简单，但贪心算法的难点在于证明"局部最优能导致全局最优"。本文系统梳理贪心算法的核心思想、适用场景，通过区间调度、跳跃游戏、加油站等经典问题，帮助读者建立完整的贪心算法解题框架。

系列导航

📚 LeetCode 算法精讲系列（共 10 篇）：

哈希表（两数之和、最长连续序列、字母异位词分组）
双指针技巧（对撞指针、快慢指针、滑动窗口）
链表操作（反转、环检测、合并）
滑动窗口技巧
二分查找
二叉树遍历与构造（前中后序、层序、构造）
动态规划入门（一维/二维 DP 、状态转移）
回溯算法（排列、组合、剪枝）
→ 贪心算法（区间调度、跳跃游戏）← 当前文章
栈与队列（括号匹配、单调栈）

什么是贪心算法？

核心思想

贪心算法（ Greedy Algorithm）是一种在每一步选择中都采取当前状态下最优选择的算法思想。贪心算法不会考虑整体最优，只关注局部最优，期望通过局部最优选择达到全局最优。

贪心算法的特点：

局部最优性：每一步都做出当前看来最好的选择
不可撤销性：一旦做出选择，就不再改变（不同于回溯）
简单高效：通常时间复杂度较低（或）
需要证明：局部最优是否能导致全局最优需要严格证明

贪心 vs 动态规划 vs 回溯：

特性	贪心算法	动态规划	回溯算法
决策方式	局部最优	全局最优	尝试所有可能
时间复杂度	或	或更高	或
适用场景	满足贪心选择性质	最优子结构+重叠子问题	搜索所有解
可撤销性	不可撤销	不可撤销	可撤销

贪心算法的两个关键性质

1. 贪心选择性质（ Greedy Choice Property）

问题的全局最优解可以通过一系列局部最优选择（贪心选择）来达到。换句话说，可以做出一个看起来最优的选择，然后求解剩余子问题。

示例：活动选择问题 - 问题：给定一组活动，每个活动有开始时间和结束时间，选择最多的不冲突活动 - 贪心策略：每次选择结束时间最早的活动 - 证明：选择结束时间最早的活动后，留给后续活动的时间最多

2. 最优子结构（ Optimal Substructure）

问题的最优解包含其子问题的最优解。做出贪心选择后，原问题简化为一个规模更小的相似子问题。

贪心算法的设计步骤

理解问题：明确目标（最大化/最小化什么）和约束条件
确定贪心策略：找到每一步的"局部最优"选择标准
证明正确性：证明局部最优能导致全局最优（反证法、交换论证）
实现算法：通常需要排序等预处理
分析复杂度：通常是或（排序）

常见的贪心策略

按结束时间排序：区间调度问题
按开始时间排序：会议室分配问题
按价值密度排序：背包问题（分数背包）
按长度排序：拼接字符串问题
按差值排序：任务分配问题
局部调整：跳跃游戏、加油站

LeetCode 435: 无重叠区间（区间调度）

给定一个区间的集合 intervals，其中 intervals[i] = [starti, endi]。返回需要移除区间的最小数量，使剩余区间互不重叠。

示例：

输入：intervals = [[1,2],[2,3],[3,4],[1,3]]
输出：1（移除 [1,3]，剩余 [[1,2],[2,3],[3,4]] 互不重叠）

约束条件：

问题分析

无重叠区间问题的本质是区间调度问题：在一组区间中，选择最多的互不重叠区间。移除区间的最小数量 = 总区间数 - 最多不重叠区间数。

核心挑战：

如何判断区间重叠：区间和重叠当且仅当且 2. 如何选择保留哪些区间：需要找到一个贪心策略
如何证明贪心策略的正确性：证明局部最优能导致全局最优

关键洞察：

贪心策略：按照区间的结束时间排序，每次选择结束时间最早且与已选区间不重叠的区间。

为什么按结束时间排序： - 选择结束时间最早的区间，能为后续区间留出最多的空间 - 结束越早，后面能容纳的区间越多 - 这是经典的"活动选择问题"（ Activity Selection Problem）

解题思路

算法流程：

排序：按区间的结束时间升序排序
初始化：选择第一个区间（结束时间最早），记录当前区间的结束时间
遍历：从第二个区间开始
- 如果当前区间的开始时间 ≥ 上一个选中区间的结束时间：不重叠，选择当前区间
- 否则：重叠，跳过当前区间（即需要移除）
返回：总区间数 - 选中的区间数 = 需要移除的区间数

贪心策略的正确性证明：

使用交换论证（ Exchange Argument）：

假设存在最优解，其中第一个选择的区间不是结束时间最早的区间，而是另一个区间（）。

将中的替换为，得到新解
因为，所以与其他区间的兼容性至少和一样好
仍然是最优解，且第一个区间是结束时间最早的
因此，总是选择结束时间最早的区间不会影响最优性

复杂度分析

时间复杂度： - 排序： - 遍历： - 总时间复杂度： 空间复杂度： - 排序的空间复杂度（取决于排序算法） - Python 的 sort() 是 Timsort，空间复杂度 - 如果使用原地排序（如快排），空间复杂度（递归栈）

复杂度证明：

排序是瓶颈，决定了总时间复杂度为。

代码实现：

from typing import List

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        """
        计算需要移除的最小区间数，使剩余区间不重叠
        
        算法步骤：
        1. 按结束时间升序排序区间
        2. 初始化：选择第一个区间，记录结束时间
        3. 遍历剩余区间：
           a. 如果当前区间开始时间 >= 上一个结束时间：不重叠，选择
           b. 否则：重叠，跳过（计数+1）
        4. 返回跳过的区间数
        
        边界条件：
        - 空数组：返回 0
        - 单区间：返回 0（无需移除）
        
        优化技巧：
        - 按结束时间排序，贪心选择结束最早的区间
        - 只需记录上一个选中区间的结束时间，无需存储所有
        
        变量含义：
        - intervals: 输入的区间列表
        - count: 保留的区间数量
        - last_end: 上一个选中区间的结束时间
        """
        if not intervals:
            return 0
        
        # 关键：按结束时间升序排序
        intervals.sort(key=lambda x: x[1])
        
        count = 1  # 至少保留第一个区间
        last_end = intervals[0][1]  # 第一个区间的结束时间
        
        # 从第二个区间开始遍历
        for i in range(1, len(intervals)):
            # 如果当前区间不与上一个重叠
            if intervals[i][0] >= last_end:
                count += 1  # 选择当前区间
                last_end = intervals[i][1]  # 更新结束时间
            # 否则重叠，跳过当前区间（不选）
        
        # 需要移除的区间数 = 总数 - 保留的数量
        return len(intervals) - count

算法原理：

为什么按结束时间排序是最优的：

考虑两个重叠的区间和，其中：

1
2
3

A: [----]
B: [----------]
    ↑ 重叠部分

如果选择： - 结束得早，后面有更多空间容纳其他区间 - 例如：[0,2], [1,5], [3,6]，选 [0,2] 后还能选 [3,6]

如果选择： - 结束得晚，占用更多时间 - 例如：[0,2], [1,5], [3,6]，选 [1,5] 后无法选 [3,6]

因此，选择结束时间早的区间总是更优。

执行过程示例（intervals = [[1,2],[2,3],[3,4],[1,3]]）：

排序后：[[1,2], [2,3], [1,3], [3,4]]  # 按结束时间排序

初始： count=1, last_end=2  # 选择 [1,2]
i=1: [2,3], start=2 >= last_end=2 ✅ 不重叠
     count=2, last_end=3  # 选择 [2,3]
i=2: [1,3], start=1 < last_end=3 ❌ 重叠，跳过
i=3: [3,4], start=3 >= last_end=3 ✅ 不重叠
     count=3, last_end=4  # 选择 [3,4]

保留 3 个区间，移除 4-3=1 个区间

常见错误：

错误一：按开始时间排序

# ❌ 错误：按开始时间排序
intervals.sort(key=lambda x: x[0])
# 反例：[[1,10],[2,3],[4,5]]
# 按开始时间排序后选 [1,10]，无法选 [2,3] 和 [4,5]
# 但最优解是移除 [1,10]，保留 [2,3] 和 [4,5]

# ✅ 正确：按结束时间排序
intervals.sort(key=lambda x: x[1])

错误二：重叠判断错误

# ❌ 错误：使用 > 判断不重叠
if intervals[i][0] > last_end:  # 会漏掉 [1,2] 和 [2,3] 的情况

# ✅ 正确：使用 >= 判断不重叠
if intervals[i][0] >= last_end:  # [1,2] 和 [2,3] 不重叠

变体扩展：

变体一：最多不重叠区间数

LeetCode 452：直接返回保留的区间数（不需要减法）

def findMinArrowShots(self, points: List[List[int]]) -> int:
    """返回最多不重叠区间数（需要的最少箭数）"""
    if not points:
        return 0
    points.sort(key=lambda x: x[1])
    count = 1
    last_end = points[0][1]
    for i in range(1, len(points)):
        if points[i][0] > last_end:  # 注意：用 > 不是 >=（因为边界重叠也算重叠）
            count += 1
            last_end = points[i][1]
    return count

LeetCode 55: 跳跃游戏

给定一个非负整数数组 nums，你最初位于数组的第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标。

示例：

输入：nums = [2,3,1,1,4]
输出：true（跳 1 步到下标 1，再跳 3 步到最后）
输入：nums = [3,2,1,0,4]
输出：false（无法越过下标 3 的 0）

约束条件：

问题分析

跳跃游戏的核心是判断能否到达终点。需要维护一个"能够到达的最远位置"。

核心挑战：

0 的陷阱：如果在某个位置跳跃距离为 0，可能无法前进
最远距离的维护：如何高效地更新和判断最远可达位置
遍历策略：是否需要遍历所有位置

关键洞察：

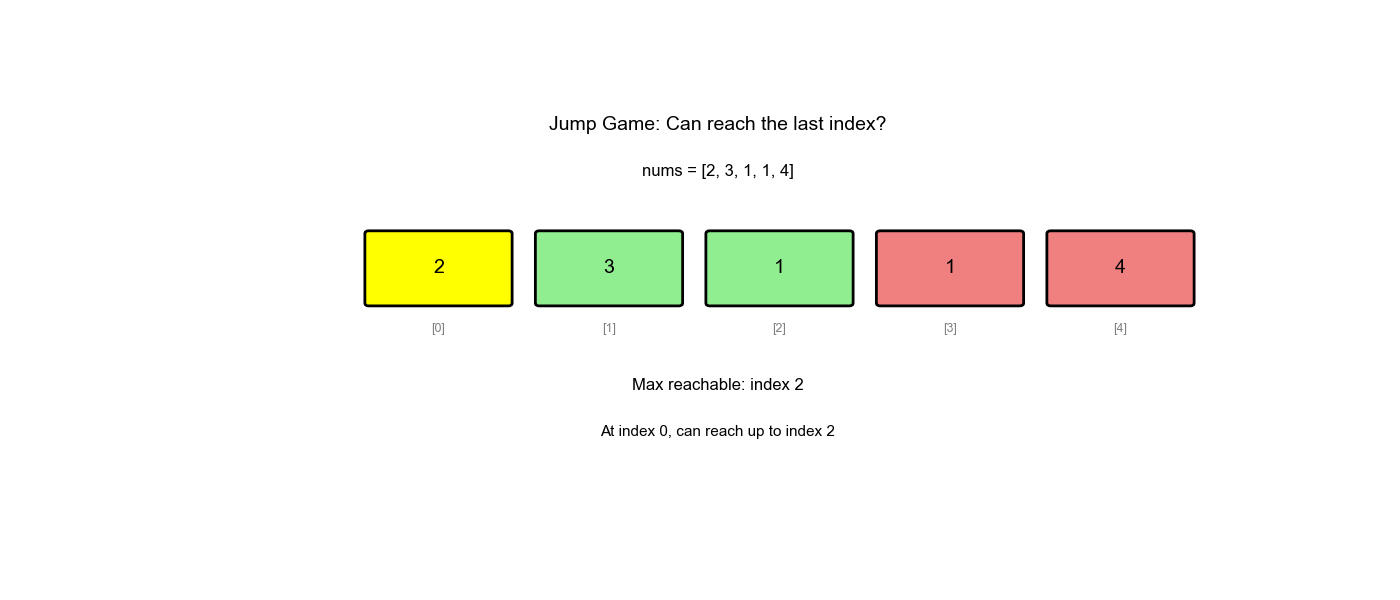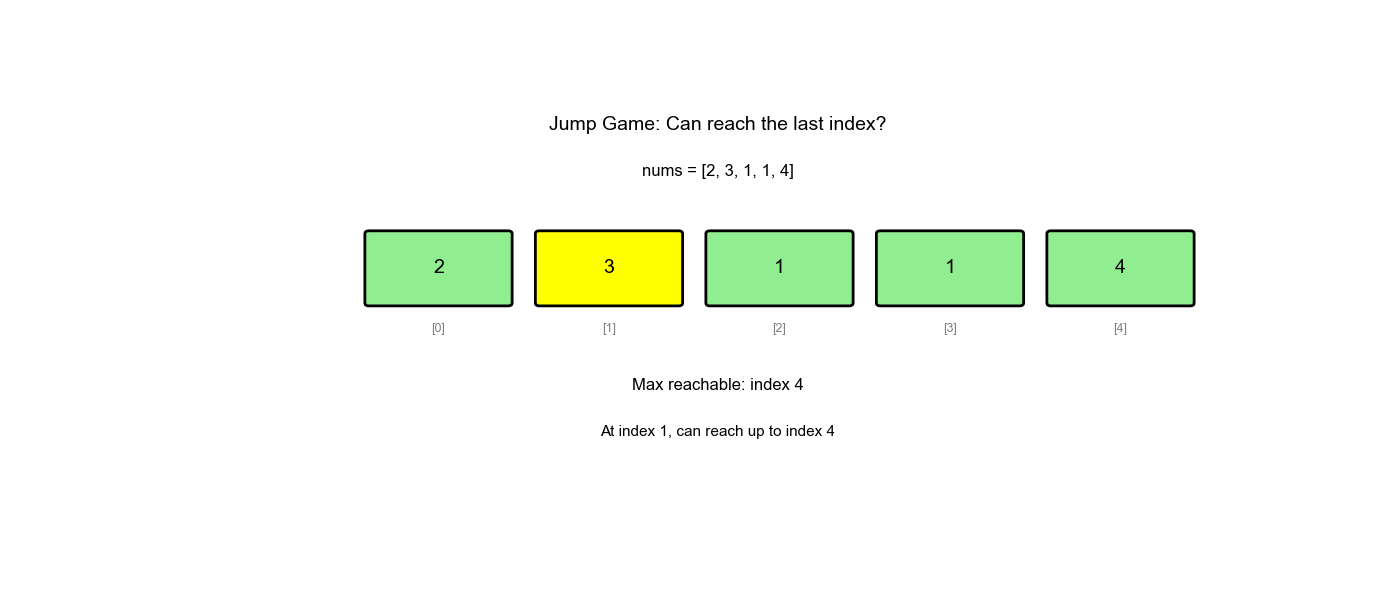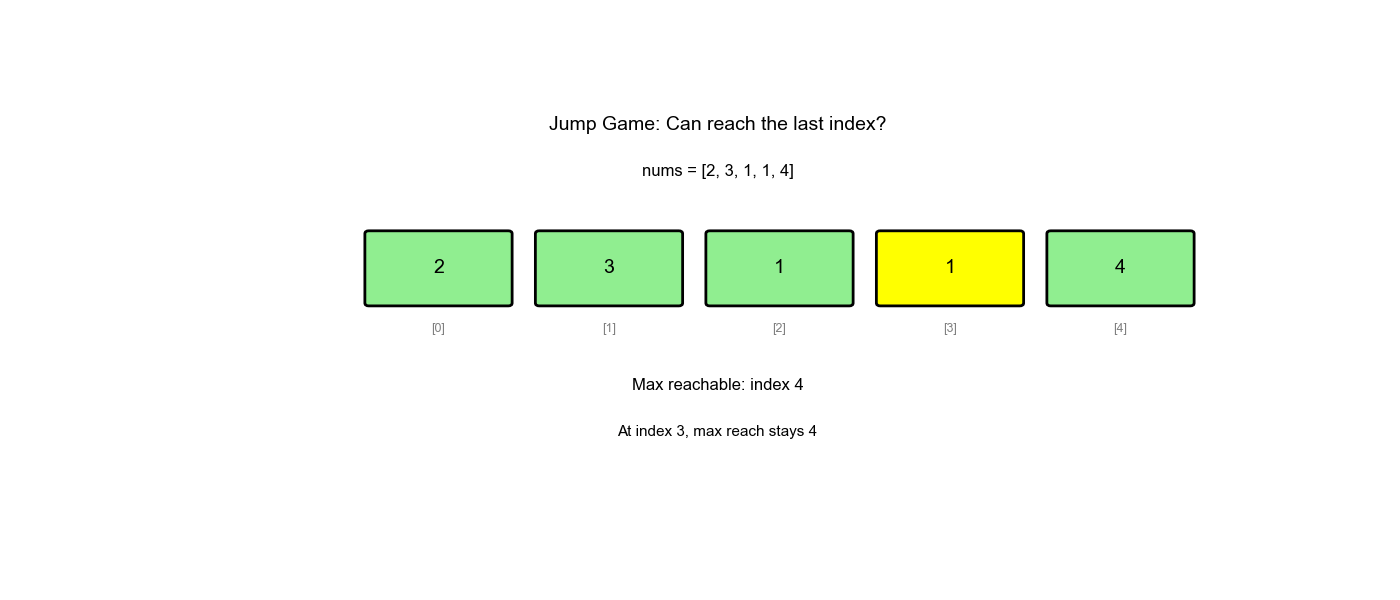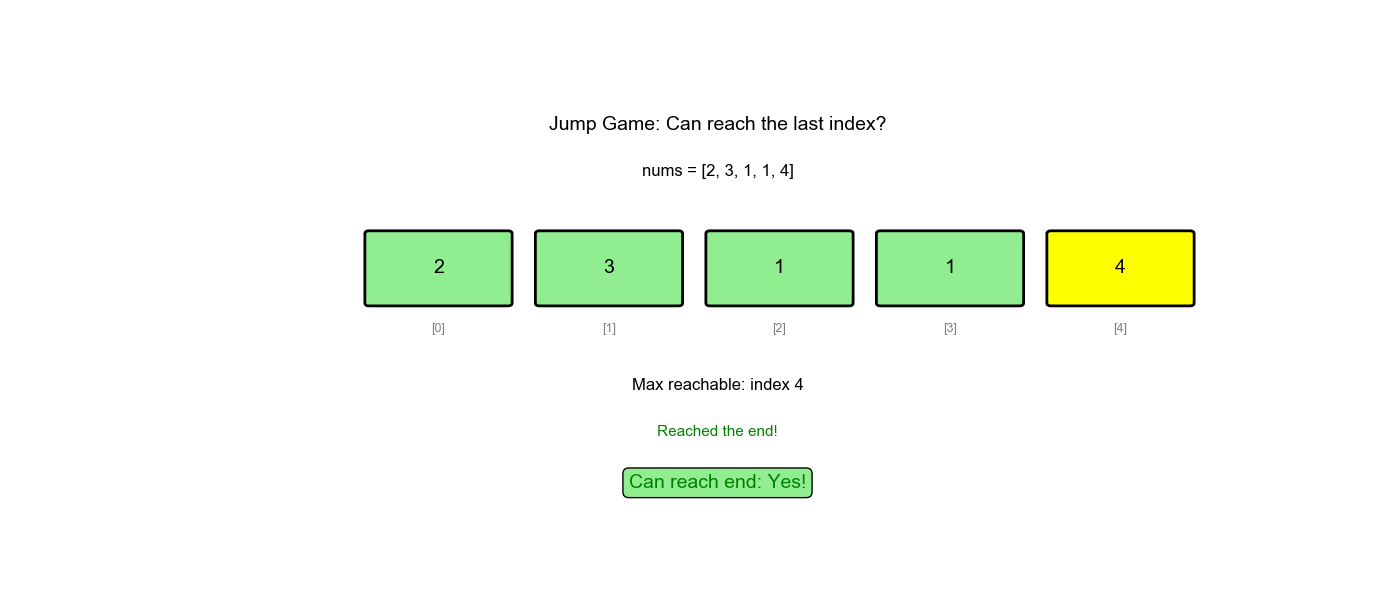
贪心策略：维护一个变量 max_reach 表示当前能到达的最远位置。遍历数组，不断更新 max_reach，如果当前位置超过了 max_reach，说明无法到达。

为什么贪心可行： - 我们不需要知道具体怎么跳，只需要知道"能不能到" - 只要当前位置可达，就更新从该位置能跳到的最远位置 - 如果最远位置 ≥ 数组末尾，说明可达

解题思路

算法流程：

初始化：max_reach = 0（从第 0 个位置开始，最远能到 0）
遍历：对于每个位置（从 0 到 n-1）
- 如果：说明无法到达位置，返回 false
- 更新：max_reach = max(max_reach, i + nums[i])（从位置能跳到的最远位置）
- 如果 max_reach >= n-1：已经能到达终点，返回 true
返回：true（遍历完成，说明所有位置都可达）

为什么是贪心：

我们不关心具体的跳跃路径，只关心"能到达的最远位置"。每一步都尽可能扩大可达范围，这是局部最优策略，也能保证全局最优（要么到达终点，要么无法到达）。

复杂度分析

时间复杂度： - 只需遍历数组一次 - 每个位置只访问一次，每次操作 空间复杂度： - 只使用常数个变量（max_reach）

复杂度证明：

遍历数组一次，每次更新 max_reach 只需要时间，因此总时间复杂度为。

代码实现：

from typing import List

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        """
        判断是否能跳到最后一个位置
        
        算法步骤：
        1. 初始化 max_reach=0（当前能到达的最远位置）
        2. 遍历数组每个位置 i：
           a. 如果 i > max_reach：无法到达位置 i，返回 false
           b. 更新 max_reach = max(max_reach, i + nums[i])
           c. 如果 max_reach >= n-1：已能到达终点，返回 true
        3. 遍历完成，返回 true
        
        边界条件：
        - 单元素：返回 true（已在终点）
        - 第一个元素为 0： max_reach=0，无法前进，返回 false（除非数组长度为 1）
        
        优化技巧：
        - 贪心：只维护最远可达位置，无需记录路径
        - 提前返回：一旦 max_reach >= n-1，立即返回
        
        变量含义：
        - max_reach: 当前能够到达的最远位置索引
        - i: 当前位置索引
        - nums[i]: 从位置 i 能跳跃的最大距离
        """
        max_reach = 0  # 当前能到达的最远位置
        n = len(nums)
        
        for i in range(n):
            # 如果当前位置超出可达范围，无法到达
            if i > max_reach:
                return False
            
            # 更新最远可达位置
            # i + nums[i] 表示从位置 i 能跳到的最远位置
            max_reach = max(max_reach, i + nums[i])
            
            # 提前返回：如果已经能到达终点
            if max_reach >= n - 1:
                return True
        
        return True  # 遍历完成，所有位置都可达

算法原理：

为什么更新 max_reach = max(max_reach, i + nums[i]) 是正确的：

i 是当前位置
nums[i] 是从当前位置能跳的最大距离
i + nums[i] 是从当前位置能到达的最远位置
max(max_reach, i + nums[i]) 确保 max_reach 始终是"到目前为止能到达的最远位置"

执行过程示例（nums = [2,3,1,1,4]）：

初始： max_reach = 0

i=0: nums[0]=2, max_reach = max(0, 0+2) = 2  # 从位置 0 能跳到位置 2
i=1: nums[1]=3, max_reach = max(2, 1+3) = 4  # 从位置 1 能跳到位置 4 ✅ 已达终点
返回 true

执行过程示例（nums = [3,2,1,0,4]）：

初始： max_reach = 0

i=0: nums[0]=3, max_reach = max(0, 0+3) = 3  # 从位置 0 能跳到位置 3
i=1: nums[1]=2, max_reach = max(3, 1+2) = 3  # 从位置 1 能跳到位置 3，未更新
i=2: nums[2]=1, max_reach = max(3, 2+1) = 3  # 从位置 2 能跳到位置 3，未更新
i=3: nums[3]=0, max_reach = max(3, 3+0) = 3  # 从位置 3 能跳到位置 3，未更新
i=4: i=4 > max_reach=3  # 位置 4 超出可达范围 ❌
返回 false

常见错误：

错误一：没有检查当前位置是否可达

# ❌ 错误：直接更新 max_reach，没有检查 i 是否可达
for i in range(n):
    max_reach = max(max_reach, i + nums[i])  # 如果 i 不可达，这样更新是错误的

# ✅ 正确：先检查 i 是否可达
for i in range(n):
    if i > max_reach:
        return False  # i 不可达
    max_reach = max(max_reach, i + nums[i])

错误二：提前返回条件错误

# ❌ 错误：检查 max_reach == n-1
if max_reach == n - 1:
    return True  # 如果 max_reach > n-1 也应该返回 true

# ✅ 正确：检查 max_reach >= n-1
if max_reach >= n - 1:
    return True

变体扩展：

变体一：跳跃游戏 II（最少跳跃次数）

LeetCode 45：给定数组 nums，保证一定能到达最后一个位置，返回到达最后一个位置的最少跳跃次数。

思路：使用贪心 + 双指针

def jump(self, nums: List[int]) -> int:
    """
    返回跳到最后一个位置的最少跳跃次数
    
    贪心策略：
    - 在当前能到达的范围内，选择能跳得最远的位置作为下一跳
    - 使用双指针维护当前跳跃范围
    """
    jumps = 0  # 跳跃次数
    current_end = 0  # 当前跳跃能到达的最远位置
    farthest = 0  # 下一跳能到达的最远位置
    
    for i in range(len(nums) - 1):  # 不需要遍历最后一个位置
        # 更新下一跳能到达的最远位置
        farthest = max(farthest, i + nums[i])
        
        # 到达当前跳跃的边界
        if i == current_end:
            jumps += 1  # 必须跳一次
            current_end = farthest  # 更新边界
            
            # 提前返回：已经能到达终点
            if current_end >= len(nums) - 1:
                break
    
    return jumps

示例（nums = [2,3,1,1,4]）：

初始： jumps=0, current_end=0, farthest=0

i=0: farthest = max(0, 0+2) = 2
     i == current_end， jumps=1, current_end=2
i=1: farthest = max(2, 1+3) = 4
i=2: farthest = max(4, 2+1) = 4
     i == current_end， jumps=2, current_end=4
     current_end >= n-1， break

返回 jumps=2

LeetCode 134: 加油站

在一条环路上有个加油站，其中第个加油站有汽油 gas[i] 升。你有一辆油箱容量无限的汽车，从第个加油站开往第个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。给定两个整数数组 gas 和 cost，如果可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。如果存在解，则保证它是唯一的。

示例：

输入：gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出：3（从加油站 3 出发：油量 3 →到 4 油量 2 →到 0 油量 0 →到 1 油量 1 →到 2 油量 2 →到 3 油量 3）

约束条件：

问题分析

加油站问题的核心是判断从哪个加油站出发能完成一圈。

核心挑战：

环形结构：需要考虑从任意位置出发绕一圈
无解的判断：何时确定无解
起点的选择：如何快速找到正确的起点

关键洞察：

贪心策略： 1. 如果总油量 < 总消耗，一定无解 2. 如果总油量 ≥ 总消耗，一定有解（且解唯一） 3. 从某个起点出发，如果在中途某个位置油量不足，说明起点到该位置之间的所有站点都不能作为起点（因为从起点到该位置的累计油量一直在下降） 4. 因此，将起点设置为下一个加油站，继续尝试

为什么贪心可行： - 如果从出发，无法到达 $ j $（$ i < j $），那么从$ i $到$ j $之间的任何加油站出发也无法到达$ j $证明：如果从$ k $（$ i < k < j $）出发能到达$ j $，那么从$ i $出发到$ k $时油量，从$ k $继续也能到达$ j$，矛盾

解题思路

算法流程：

判断无解：如果 sum(gas) < sum(cost)，返回 -1
初始化：start = 0（起始加油站），total_tank = 0（当前油量），current_tank = 0（从 start 出发的累计油量）
遍历：对于每个加油站 - 计算净油量：current_tank += gas[i] - cost[i]
- 如果 current_tank < 0：无法从 start 到达，将 start 设为，重置 current_tank = 0
返回：start

复杂度分析

时间复杂度： - 只需遍历数组一次或两次（判断总和 + 遍历）

空间复杂度： - 只使用常数个变量

代码实现：

from typing import List

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        """
        判断从哪个加油站出发能绕一圈，返回起始加油站索引
        
        算法步骤：
        1. 判断无解： sum(gas) < sum(cost)，返回-1
        2. 初始化： start=0, total_tank=0, current_tank=0
        3. 遍历每个加油站 i：
           a. 计算净油量： gas[i] - cost[i]
           b. 累加到 total_tank 和 current_tank
           c. 如果 current_tank < 0：起点设为 i+1，重置 current_tank
        4. 返回 start
        
        边界条件：
        - 单加油站：检查 gas[0] >= cost[0]
        - 总油量不足：返回-1
        
        优化技巧：
        - 贪心：如果从 i 无法到达 j，则 i 到 j 之间的任何站点都不能作为起点
        - 一次遍历：同时计算总油量和寻找起点
        
        变量含义：
        - start: 起始加油站索引
        - total_tank: 总油量 - 总消耗
        - current_tank: 从 start 出发的累计油量
        """
        n = len(gas)
        total_tank = 0  # 总油量 - 总消耗
        current_tank = 0  # 从 start 出发的累计油量
        start = 0  # 起始加油站
        
        for i in range(n):
            total_tank += gas[i] - cost[i]
            current_tank += gas[i] - cost[i]
            
            # 如果当前油量不足，无法从 start 到达 i+1
            if current_tank < 0:
                start = i + 1  # 起点设为下一个加油站
                current_tank = 0  # 重置油量
        
        # 如果总油量不足，无解
        return start if total_tank >= 0 else -1

算法原理：

为什么如果总油量够就一定有解：

假设总油量 ≥ 总消耗，即。

如果从某个起点出发，在位置油量不足，说明从到的累计油量 < 0 。

根据贪心策略，我们将起点设为。由于总油量 ≥ 0，从出发一定能补偿之前的亏损，最终完成一圈。

常见错误：

错误一：暴力尝试每个起点

# ❌ 错误：时间复杂度 O(n^2)
for start in range(n):
    tank = 0
    for i in range(n):
        tank += gas[(start + i) % n] - cost[(start + i) % n]
        if tank < 0:
            break
    if tank >= 0:
        return start

# ✅ 正确：贪心算法 O(n)

总结

核心要点

贪心算法的本质：在每一步选择中都采取当前状态下最优的选择，期望通过局部最优达到全局最优
贪心算法的难点：证明局部最优能导致全局最优（需要数学证明）
常见贪心策略：
- 排序：按某种属性排序后贪心选择
- 维护最优值：动态更新和维护最优值（如最远距离）
- 局部调整：根据当前状态做出最优调整

解题清单

区间调度类：

✅ 无重叠区间（按结束时间排序）
✅ 用最少数量的箭引爆气球（区间重叠）
会议室问题（区间调度）

跳跃游戏类：

✅ 跳跃游戏（判断能否到达）
✅ 跳跃游戏 II（最少跳跃次数）

加油站类：

✅ 加油站（环形数组）
分发糖果（局部调整）

其他经典问题：

买卖股票的最佳时机 II（多次交易）
分发饼干（排序贪心）
摆动序列（局部调整）

常见错误

错误的贪心策略：没有正确选择贪心标准（如按开始时间排序而不是结束时间）
忘记证明正确性：贪心算法需要证明局部最优能导致全局最优
边界条件处理：没有处理空数组、单元素等边界情况
提前返回条件：没有在满足条件时提前返回，导致效率降低

学习建议

理解贪心的适用场景：不是所有问题都能用贪心，需要满足贪心选择性质和最优子结构
学会证明正确性：使用反证法、交换论证等方法证明贪心策略的正确性
对比动态规划：有些问题既可以用贪心也可以用 DP，理解两者的区别和适用场景
积累常见模式：区间调度、跳跃问题、分配问题等都有固定的贪心模式

常见问题 Q&A

Q1：如何判断一个问题是否可以用贪心算法？

A1：满足以下条件时可以考虑贪心： 1. 问题可以分解为子问题 2. 局部最优选择能导致全局最优（需要证明） 3. 问题具有最优子结构 4. 通常求最大值/最小值/计数问题

Q2：贪心算法和动态规划有什么区别？

A2： - 贪心：每一步做出当前最优选择，不可撤销，通常或 - 动态规划：考虑所有可能的选择，找出全局最优，通常或更高 - 适用性：贪心需要严格证明正确性， DP 适用范围更广

Q3：为什么区间调度要按结束时间排序而不是开始时间？

A3：按结束时间排序能为后续区间留出最多空间。选择结束早的区间，后面能容纳的区间越多。按开始时间排序可能选择一个很长的区间，导致后续无法选择更多区间。

Q4：跳跃游戏为什么只需要维护最远距离？

A4：我们只关心"能否到达"，不关心"如何到达"。只要当前位置可达，就更新从该位置能跳到的最远位置。如果最远位置 ≥ 终点，说明可达。

Q5：加油站问题为什么如果总油量够就一定有解？

A5：如果总油量 ≥ 总消耗，说明整体是有盈余的。如果从某个起点出发在中途油量不足，说明起点到该位置的累计油量 < 0（有亏损）。将起点设为下一个加油站，由于总油量 ≥ 0，后续的盈余一定能补偿之前的亏损，最终完成一圈。

Q6：贪心算法一定需要排序吗？

A6：不一定。有些贪心问题需要排序（如区间调度），有些不需要（如跳跃游戏、加油站）。关键是找到合适的贪心策略。

Q7：如何证明贪心算法的正确性？

A7：常用方法： 1. 反证法：假设存在更优解，推导出矛盾 2. 交换论证：证明将非贪心选择替换为贪心选择不会变差 3. 归纳法：证明每一步贪心选择后问题规模缩小，且保持最优性

Q8：贪心算法的时间复杂度一般是多少？

A8： - 不需要排序：（如跳跃游戏、加油站） - 需要排序：（如区间调度） - 通常比动态规划（或更高）和回溯（或）快得多

希望通过本文，你对贪心算法有了深入的理解。继续练习，逐步建立贪心算法的直觉和解题框架！🎯