LeetCode（三）—— 链表操作

链表是技术面试的基石，测试你操作指针、处理边界情况和优化空间使用的能力。与数组不同，链表提供 的插入和删除，但需要 进行访问。它们自然支持动态增长，但缺乏随机访问能力。本综合指南通过五个经典问题——反转链表（迭代和递归）、合并两个有序链表、检测环入口点、找到相交节点和删除倒数第 n 个节点——构建完整的链表掌握工具包。我们将深入探讨迭代与递归之间的权衡、虚拟节点的威力，以及如何在 空间中解决复杂操作。

系列导航

📚 LeetCode 算法精讲系列（共 10 篇）：

1. 哈希表完全指南
2. 双指针技巧
3. → 链表操作（反转、环检测、合并、相交、删除）← 当前文章
4. 二叉树遍历与递归
5. 动态规划基础
6. 回溯算法
7. 二分查找进阶
8. 栈与队列
9. 图算法
10. 贪心与位运算

---

链表基础回顾

链表 vs 数组

特性	数组	链表
访问
插入/删除（已知位置）	（需要移位）
内存	连续	非连续
缓存局部性	✅ 高	❌ 低
动态增长	⚠️ 需要重新分配	✅ 自然支持

链表节点定义

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

链表的思维模型

将链表想象成一列火车：

• 节点：每节车厢
• 指针：连接车厢的耦合器
• 头节点：机车
• 尾节点：最后一节车厢（next = None）

操作直觉：

• 反转：让火车倒着运行
• 合并：按顺序合并两列火车
• 检测环：检查火车是否形成环路
• 删除节点：移除一节车厢并重新连接其余部分

---

LeetCode 206: 反转链表

问题分析

核心难点：如何在一次遍历中反转所有指针方向，而不使用额外的 空间存储节点。链表只能顺序访问，无法像数组那样随机访问，这增加了操作的复杂性。

解题思路：使用三指针技术（迭代）或递归。迭代方法维护三个指针：prev（前一个节点）、curr（当前节点）、next_node（下一个节点）。在遍历过程中，将 curr.next 指向 prev，然后三个指针向前移动。递归方法先递归反转剩余部分，然后调整当前节点的指针。两种方法都能在 时间内完成，但迭代方法空间复杂度为 ，递归方法为 。

复杂度分析： - 时间复杂度： - 需要遍历链表一次 - 空间复杂度： - 迭代： - 仅使用常数额外指针 - 递归： - 递归栈深度

关键洞察：反转链表的本质是改变每个节点的 next 指针方向。关键是在修改指针之前保存下一个节点的引用，避免丢失后续节点。

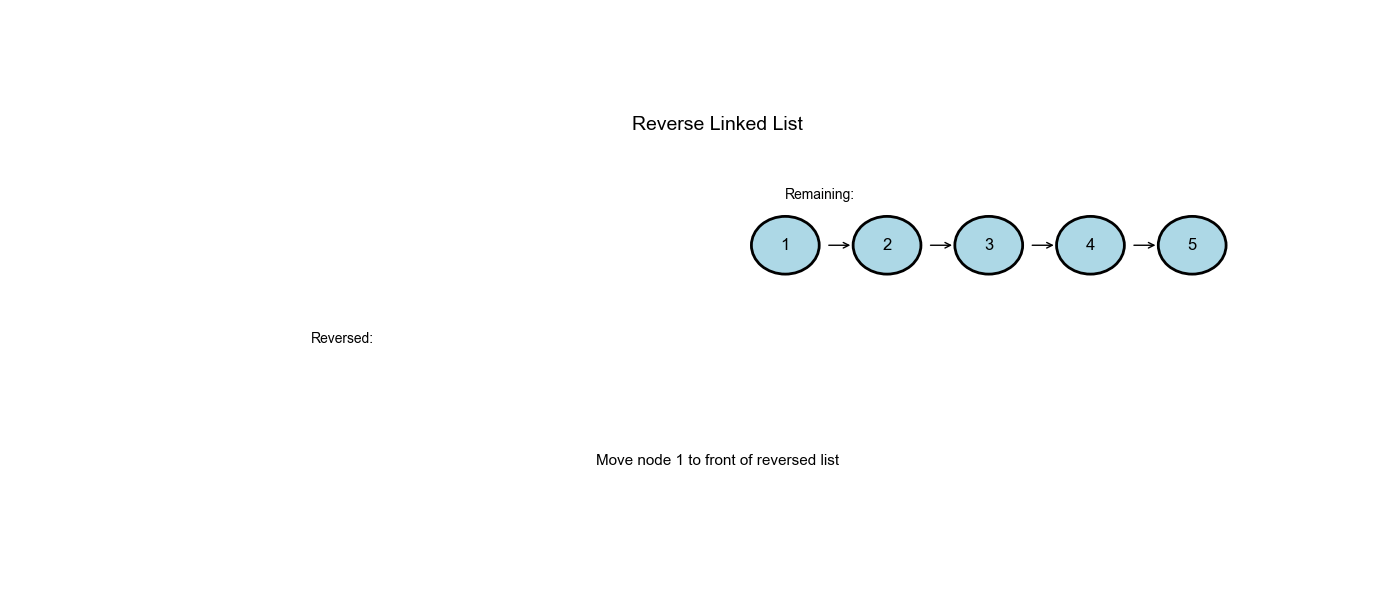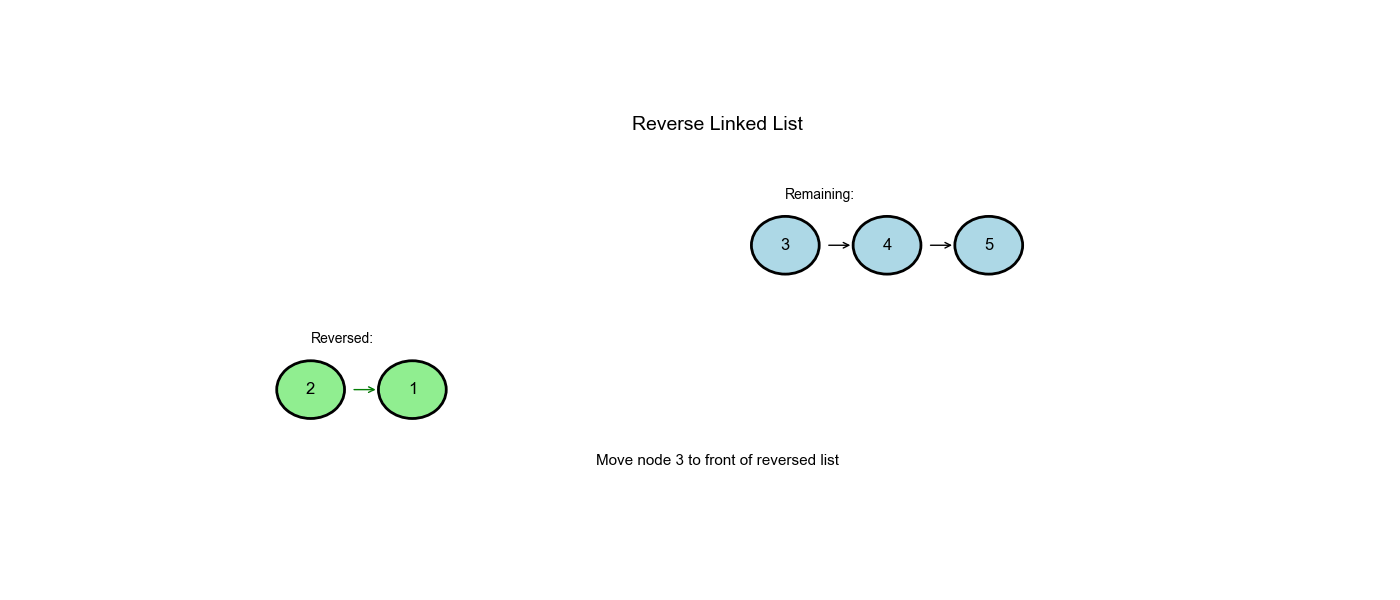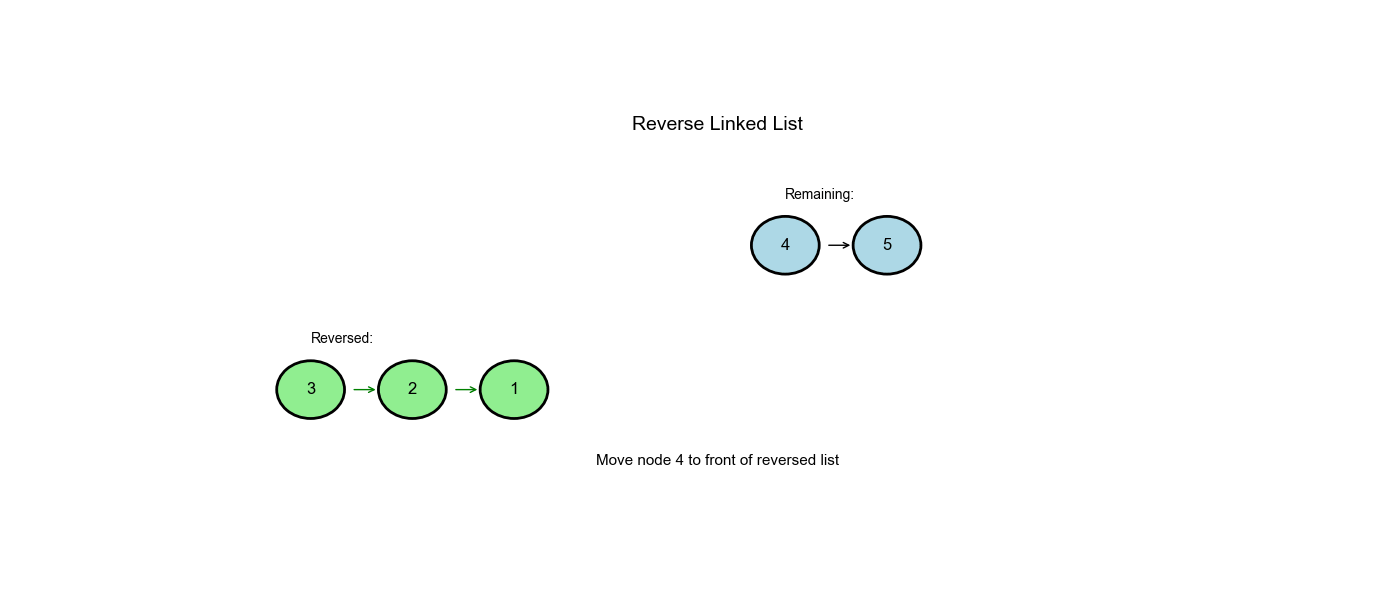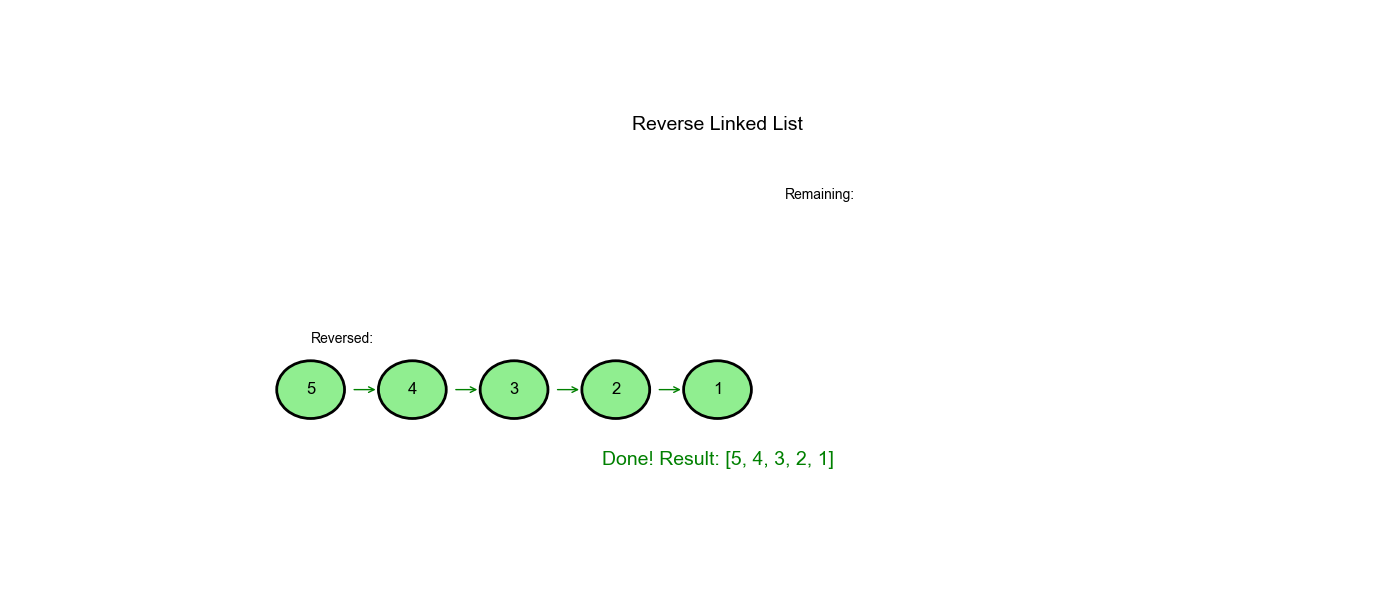
问题描述

给你单链表的头节点 head，请你反转链表，并返回反转后的链表。

示例：

• 输入：head = [1,2,3,4,5]
• 输出：[5,4,3,2,1]

约束条件：

• 链表中节点的数目范围是
• 进阶：可以用迭代或递归两种方法解决这个问题吗？

方法一：迭代（三指针技术）

核心思想

维护三个指针：

• prev：前一个节点
• curr：当前节点
• next_node：下一个节点（临时存储）

步骤：

1. 初始化 prev = None，curr = head

2. 遍历链表，每次迭代：

   • 将 curr.next 保存到 next_node
   • 反转指针：curr.next = prev
   • 移动指针：prev = curr，curr = next_node

3. 返回 prev（新头节点）

Python 实现

def reverseList(head):
    """
    使用三指针迭代反转链表。
  
    时间复杂度： O(n) - 单次遍历链表
    空间复杂度： O(1) - 仅使用常数额外空间
    """
    # prev: 前一个节点，初始为 None（新链表的尾节点）
    prev = None
    # curr: 当前正在处理的节点，从头节点开始
    curr = head
  
    # 遍历链表，直到处理完所有节点
    while curr:
        # 关键步骤 1：在修改指针之前保存下一个节点
        # 如果不保存，修改 curr.next 后会丢失后续节点
        next_node = curr.next
      
        # 关键步骤 2：反转指针
        # 将当前节点的 next 指向前一个节点（ prev）
        # 这样就反转了当前节点与前一个节点的连接
        curr.next = prev
      
        # 关键步骤 3：向前移动两个指针
        # prev 移动到当前节点（成为下一个节点的"前一个"）
        prev = curr
        # curr 移动到下一个节点（继续处理）
        curr = next_node
  
    # 循环结束时， prev 指向原链表的尾节点，即新链表的头节点
    # curr 为 None（已处理完所有节点）
    return prev

复杂度分析

• 时间复杂度：，单次遍历
• 空间复杂度：，仅使用常数额外指针

逐步解析

输入：1 → 2 → 3 → None

步骤	prev	curr	next_node	操作	链表状态
初始	None	1	-	-	1 → 2 → 3 → None
1	None	1	2	保存 2	-
1	None	1	2	1.next = None	None ← 1 2 → 3 → None
1	1	2	2	移动指针	-
2	1	2	3	保存 3	-
2	1	2	3	2.next = 1	None ← 1 ← 2 3 → None
2	2	3	3	移动指针	-
3	2	3	None	保存 None	-
3	2	3	None	3.next = 2	None ← 1 ← 2 ← 3
3	3	None	-	循环结束	-
返回	3	-	-	-	3 → 2 → 1 → None

常见错误与边界情况

错误一：丢失下一个引用

# ❌ 错误：我们丢失了对 curr.next 的引用
curr.next = prev
prev = curr
curr = curr.next  # 这现在是 prev，不是原始的下一个！

错误二：不处理空链表

# ❌ 错误：如果 head 是 None，我们错误地返回 None
def reverseList(head):
    prev = None
    curr = head
    while curr:  # 这正确处理 None，但要明确
        # ...

边界情况：

• 空链表（head = None）：返回 None ✅
• 单节点（head = [1]）：返回 [1] ✅
• 两节点（head = [1,2]）：返回 [2,1] ✅

面试技巧

面试官看重的：

1. 指针操作：你能安全地移动指针而不丢失引用吗？
2. 边界情况处理：你检查空/单节点链表吗？
3. 空间优化：你能用 空间完成吗？

后续问题：

• "你能递归地反转吗？"
• "如果链表有环怎么办？"
• "你能只反转链表的一部分吗？"

---

方法二：递归

核心思想

递归定义：反转链表 = 反转剩余部分 + 调整当前节点的指针

基本情况：空链表或单节点，原样返回

递归步骤：

1. 递归反转 head.next 并得到新头节点 new_head
2. 使 head.next.next 指向 head（反转指针）
3. 断开 head.next（防止环）
4. 返回 new_head

Python 实现

def reverseList_recursive(head):
    """
    递归反转链表。
  
    关键洞察：先反转剩余部分，
    然后调整当前节点的指针。
  
    时间复杂度： O(n) - 每个节点访问一次
    空间复杂度： O(n) - 递归栈深度
    """
    # 基本情况：空链表或单节点
    if not head or not head.next:
        return head
  
    # 递归反转剩余链表
    # new_head 将是原始尾节点，现在是新头节点
    new_head = reverseList_recursive(head.next)
  
    # 此时， head.next 是反转子链表的最后一个节点
    # 需要让它指回 head
    head.next.next = head
  
    # 断开原始链接以防止环
    head.next = None
  
    return new_head

复杂度分析

• 时间复杂度：，每个节点访问一次
• 空间复杂度：，递归栈深度

递归过程可视化

输入：1 → 2 → 3 → None

reverseList(1)
    reverseList(2)
        reverseList(3)
            reverseList(None)  # 基本情况，返回 None
        # 现在在节点 3：
        # 3.next = None，所以我们返回 3
        # 执行： 2.next.next = 2 → 3.next = 2
        # 断开： 2.next = None
        # 返回 3（ new_head）
    # 现在在节点 2：
    # 执行： 1.next.next = 1 → 2.next = 1
    # 断开： 1.next = None
    # 返回 3（ new_head）
# 最终： 3 → 2 → 1 → None

最终结果：3 → 2 → 1 → None

理解递归的魔法

递归方法向后工作：

1. 它首先到达尾节点
2. 然后，随着递归展开，它逐个反转指针
3. 递归的每一层处理一个节点的反转

为什么 head.next.next = head？

• 反转从 head.next 开始的子链表后，原本在 head.next 的节点现在是反转子链表的尾节点
• 我们希望这个尾节点指回 head
• head.next.next 访问原本在 head.next 的节点，我们让它指向 head

---

迭代 vs 递归对比

方法	时间	空间	优点	缺点
迭代			空间最优，更容易理解	代码稍长
递归			简洁，优雅	栈空间开销，潜在栈溢出

面试策略：从迭代开始（更实用），然后提及递归作为替代方法。

---

LeetCode 21: 合并两个有序链表

问题分析

核心难点：如何高效地合并两个有序链表，同时处理边界情况（空链表、一个链表先耗尽等）。需要维护结果链表的构建过程，确保节点按升序连接。

解题思路：使用虚拟节点（ dummy node）技术简化边界处理。虚拟节点作为结果链表的前驱，避免处理"第一个节点"的特殊情况。使用 current 指针跟踪当前构建位置，比较两个链表的当前节点值，将较小的节点连接到结果链表，然后移动相应指针。当一个链表耗尽时，直接将另一个链表的剩余部分连接到结果。

复杂度分析： - 时间复杂度： - 和 是两个链表的长度，每个节点访问一次 - 空间复杂度： - 仅使用常数额外指针（不包括结果链表本身）

关键洞察：虚拟节点消除了"第一个节点"的特殊情况，使代码更简洁统一。这是链表问题中常用的技巧。

问题描述

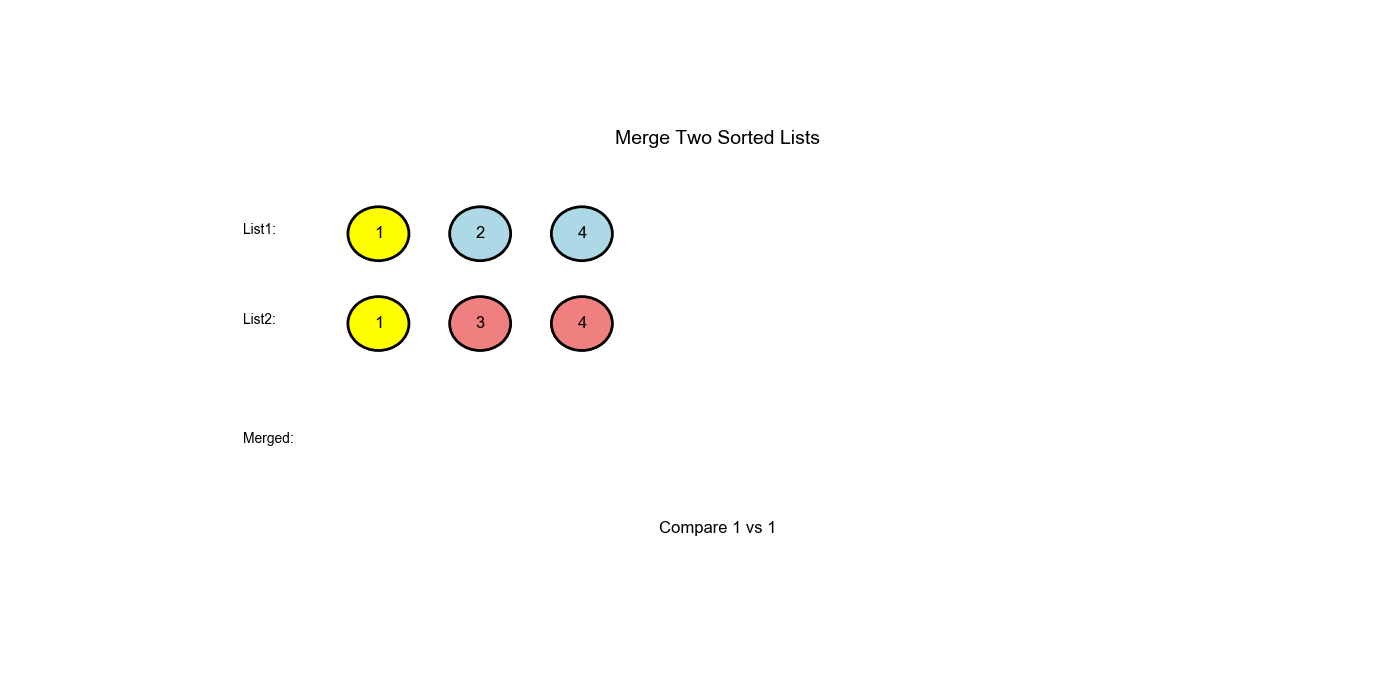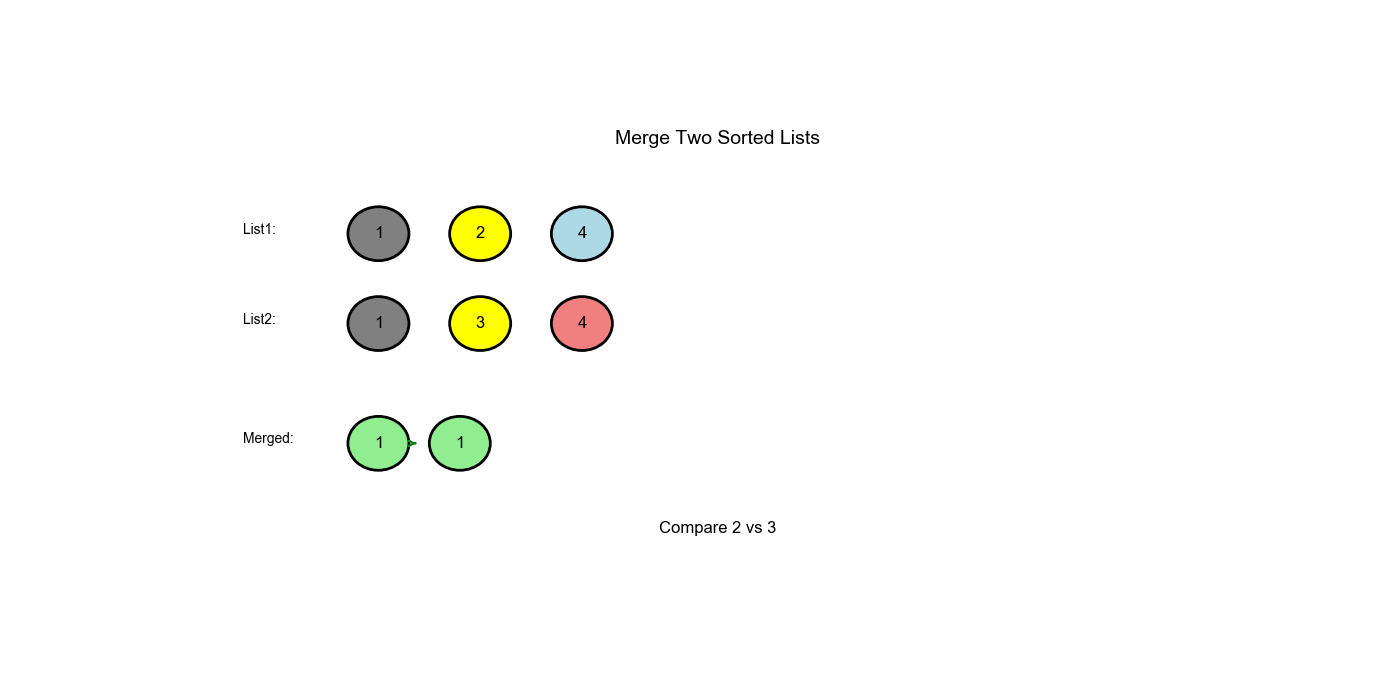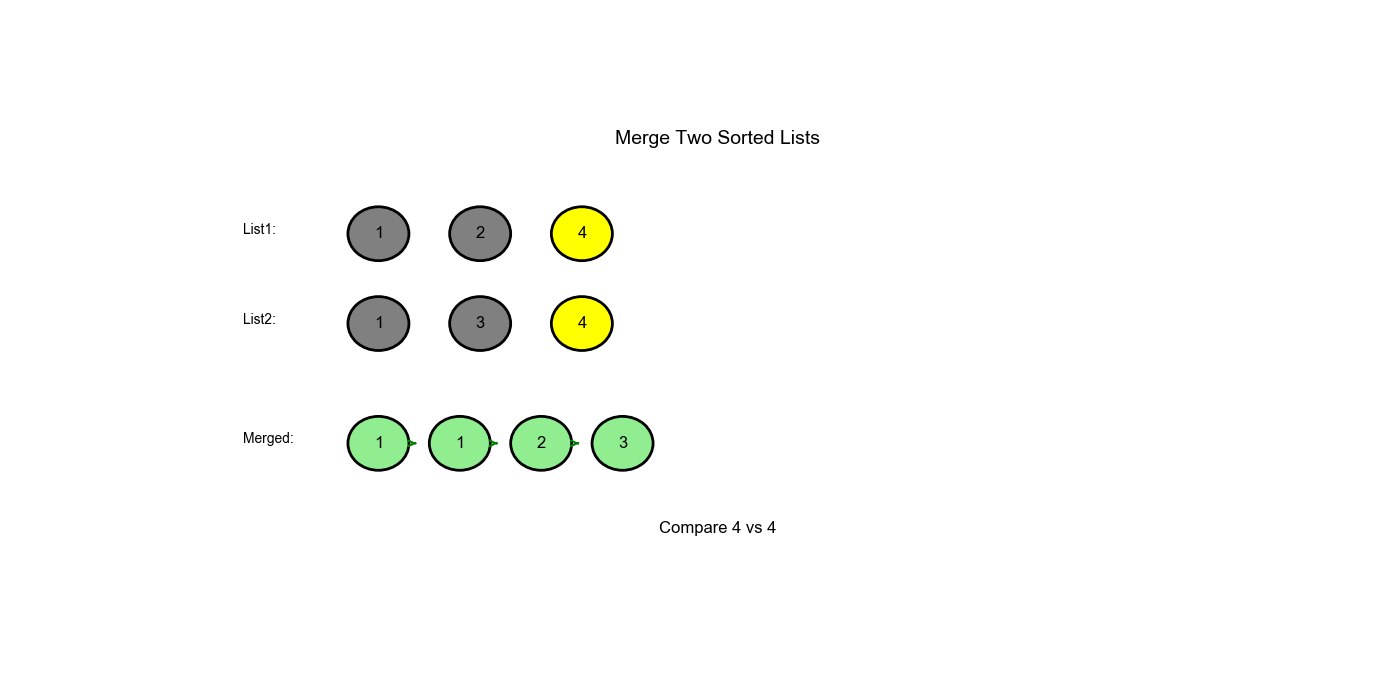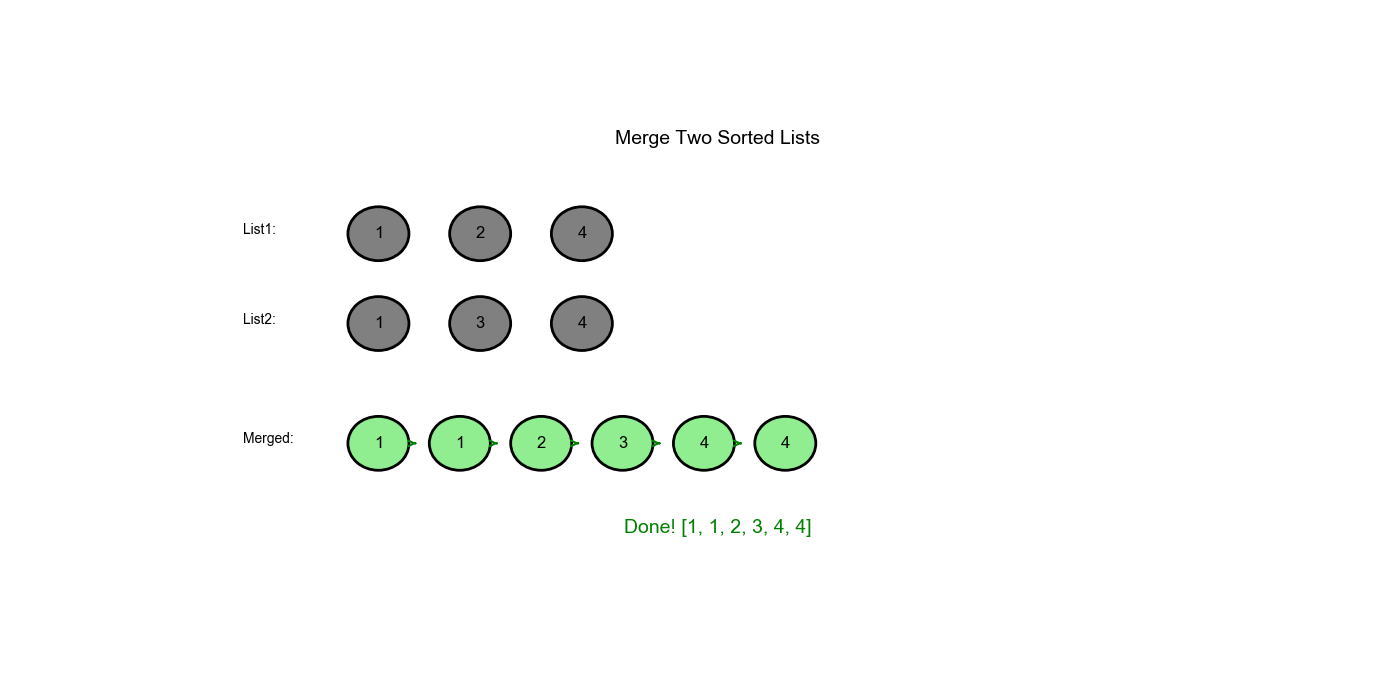
将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例：

• 输入：l1 = [1,2,4], l2 = [1,3,4]
• 输出：[1,1,2,3,4,4]

约束条件：

• 两个链表的节点数目范围是
• 两个链表均为非递减顺序

方法一：迭代（虚拟节点技术）

核心思想

使用虚拟节点（哨兵节点）简化边界处理：

1. 创建一个 dummy 节点作为结果链表的前驱
2. 使用 current 指针跟踪当前构建位置
3. 比较 l1 和 l2 的值，将较小的附加到 current
4. 处理剩余节点
5. 返回 dummy.next（跳过哨兵）

Python 实现

def mergeTwoLists(l1, l2):
    """
    使用虚拟节点迭代合并两个有序链表。
  
    虚拟节点消除了从头开始构建结果链表时的特殊情况。
  
    时间复杂度： O(m + n)，其中 m, n 是 l1, l2 的长度
    空间复杂度： O(1) - 仅使用常数额外空间
    """
    # 创建虚拟节点作为结果链表的前驱
    # 这样所有节点都可以统一处理，无需特殊处理第一个节点
    dummy = ListNode(-1)
    # current 指针跟踪当前构建位置
    # 我们将在 current 之后添加新节点
    current = dummy
  
    # 比较并合并，当两个链表都有节点时
    while l1 and l2:
        # 比较两个链表的当前节点值
        if l1.val <= l2.val:
            # l1 的值较小（或相等），将 l1 的当前节点连接到结果
            current.next = l1
            # l1 指针向前移动
            l1 = l1.next
        else:
            # l2 的值较小，将 l2 的当前节点连接到结果
            current.next = l2
            # l2 指针向前移动
            l2 = l2.next
        # current 指针向前移动，指向结果链表的最后一个节点
        current = current.next
  
    # 处理剩余节点（一个链表可能已耗尽）
    # 如果 l1 是 None，说明 l1 已耗尽，连接 l2 的剩余部分（可能为 None）
    # 如果 l2 是 None，说明 l2 已耗尽，连接 l1 的剩余部分（可能为 None）
    # 如果两者都是 None， current.next = None（正确）
    current.next = l1 if l1 else l2
  
    # 返回 dummy.next，跳过虚拟节点
    return dummy.next  # 跳过虚拟节点

复杂度分析

• 时间复杂度：，其中 和 是两个链表的长度
• 空间复杂度：，仅使用常数额外指针

深入解读

算法原理：为什么虚拟节点能简化代码？

核心思想：虚拟节点作为"占位符"，使得所有节点的处理逻辑统一。如果没有虚拟节点，需要特殊处理第一个节点（确定哪个链表提供头节点），代码会变得复杂。

为什么 current.next = l1 if l1 else l2 能正确处理剩余节点： - 如果 l1 和 l2 都非空：循环继续 - 如果 l1 为空：l2 的剩余部分（可能为空）直接连接到结果 - 如果 l2 为空：l1 的剩余部分（可能为空）直接连接到结果 - 如果两者都为空：current.next = None，正确结束

时间复杂度证明：为什么是 O(m+n)？

• 循环次数：最多 次（每个节点最多被访问一次）
• 每次迭代操作： （比较、连接、移动指针）
• 总时间：

空间优化：有没有更省空间的方法？

这个问题已经是空间最优的： - 虚拟节点：空间（一个节点） - 指针变量：空间（current, l1, l2） - 无法进一步优化：必须构建新链表

注意：结果链表本身需要 空间，但这是输出要求，不计入额外空间复杂度。

常见错误分析

错误类型	错误代码	问题	正确做法
忘记移动 current	current.next = l1; l1 = l1.next	current 不更新	current = current.next
不使用虚拟节点	直接确定头节点	需要特殊处理	使用 dummy
剩余节点处理错误	if l1: current.next = l1	可能遗漏 l2	current.next = l1 if l1 else l2

变体扩展

1. 合并 K 个有序链表：使用分治或优先队列
2. 合并两个有序链表（原地）：不创建新节点，修改原链表
3. 合并两个有序数组：类似思路，但数组需要移动元素

虚拟节点的威力

为什么需要虚拟节点？

不使用虚拟节点：

# ❌ 需要特殊处理第一个节点
def mergeTwoLists_no_dummy(l1, l2):
    if not l1:
        return l2
    if not l2:
        return l1
  
    # 确定头节点
    if l1.val <= l2.val:
        head = l1
        l1 = l1.next
    else:
        head = l2
        l2 = l2.next
  
    current = head
    # 现在合并其余部分...
    # 需要更复杂的逻辑

使用虚拟节点：

# ✅ 统一处理，无特殊情况
dummy = ListNode(-1)
current = dummy
# 所有节点的统一循环逻辑

现实类比：虚拟节点就像"施工标记"——完成后移除，但在施工过程中提供固定参考点。

逐步解析

输入：l1 = [1,2,4], l2 = [1,3,4]

步骤	l1	l2	current	操作	当前结果
初始	1	1	dummy	-	dummy → ...
1	1	1	dummy	比较：1 <= 1，附加 l1	dummy → 1
1	2	1	1	移动 l1 向前	-
2	2	1	1	比较：1 < 2，附加 l2	dummy → 1 → 1
2	2	3	1	移动 l2 向前	-
3	2	3	1	比较：2 < 3，附加 l1	dummy → 1 → 1 → 2
3	4	3	2	移动 l1 向前	-
4	4	3	2	比较：3 < 4，附加 l2	dummy → 1 → 1 → 2 → 3
4	4	4	3	移动 l2 向前	-
5	4	4	3	比较：4 <= 4，附加 l1	dummy → 1 → 1 → 2 → 3 → 4
5	None	4	4	l1 耗尽，附加 l2 的剩余部分	dummy → 1 → 1 → 2 → 3 → 4 → 4
返回	-	-	-	返回 dummy.next	1 → 1 → 2 → 3 → 4 → 4

边界情况

1. 一个链表为空：l1 = [], l2 = [1,2] → 返回 [1,2] ✅
2. 两个链表都为空：l1 = [], l2 = [] → 返回 [] ✅
3. 一个链表更长：l1 = [1], l2 = [2,3,4] → 返回 [1,2,3,4] ✅

---

方法二：递归

核心思想

递归定义：

• 如果 l1.val <= l2.val，结果是 l1 + merge(l1.next, l2)
• 否则，结果是 l2 + merge(l1, l2.next)

Python 实现

def mergeTwoLists_recursive(l1, l2):
    """
    递归合并两个有序链表。
  
    递归方法优雅但使用 O(m+n) 栈空间。
    生产环境选择迭代，面试中展示多种方法。
  
    时间复杂度： O(m + n)
    空间复杂度： O(m + n) - 递归栈
    """
    # 基本情况：如果一个链表为空，返回另一个
    if not l1:
        return l2
    if not l2:
        return l1
  
    # 递归合并：选择较小的头节点，然后合并其余部分
    if l1.val <= l2.val:
        # l1 较小，所以它成为头节点
        # 递归合并其余部分
        l1.next = mergeTwoLists_recursive(l1.next, l2)
        return l1
    else:
        # l2 较小，所以它成为头节点
        # 递归合并其余部分
        l2.next = mergeTwoLists_recursive(l1, l2.next)
        return l2

复杂度分析

• 时间复杂度：
• 空间复杂度：，递归栈

递归可视化

输入：l1 = [1,2], l2 = [3,4]

mergeTwoLists([1,2], [3,4])
    l1.val (1) <= l2.val (3) → True
    l1.next = mergeTwoLists([2], [3,4])
        l1.val (2) <= l2.val (3) → True
        l1.next = mergeTwoLists([], [3,4])
            l1 is None → return [3,4]
        return [2,3,4]
    return [1,2,3,4]

---

LeetCode 142: 环形链表 II

问题分析

核心难点：这道题在检测环的基础上，还需要找到环的入口节点。使用哈希集合需要 空间，不符合进阶要求。需要利用快慢指针相遇的数学性质来定位入口。

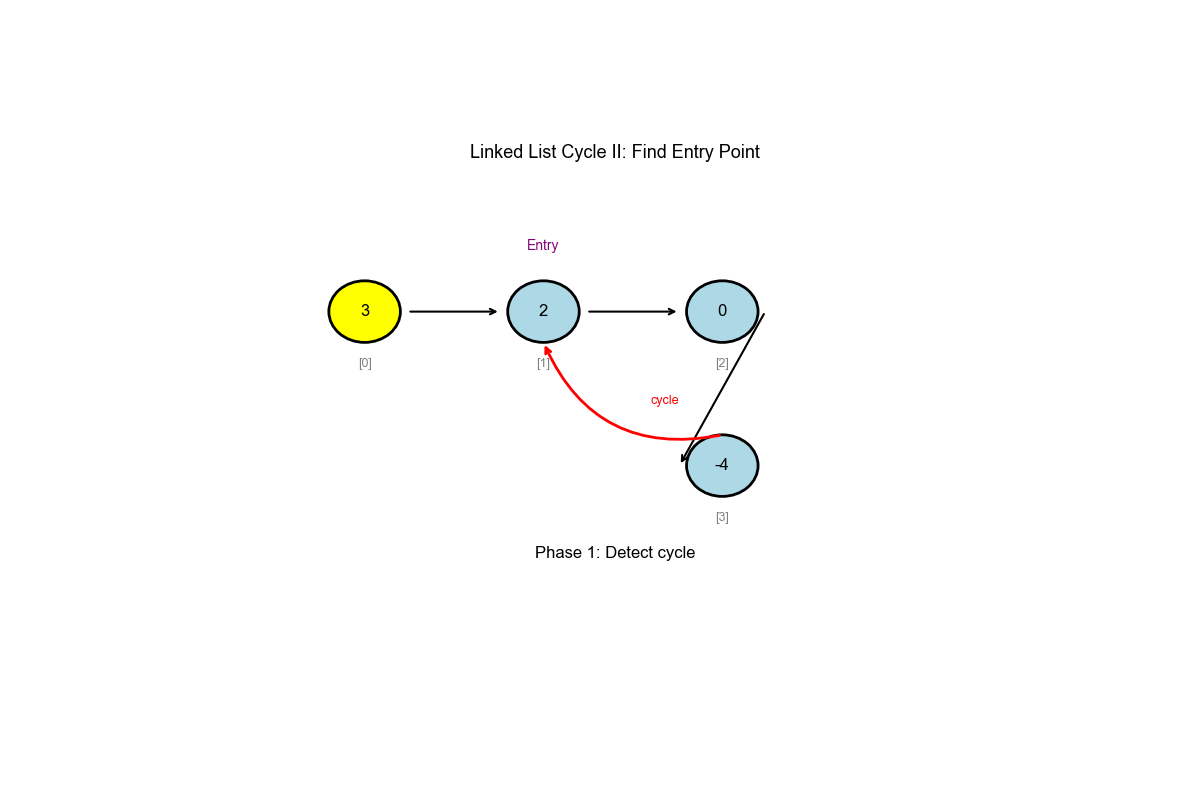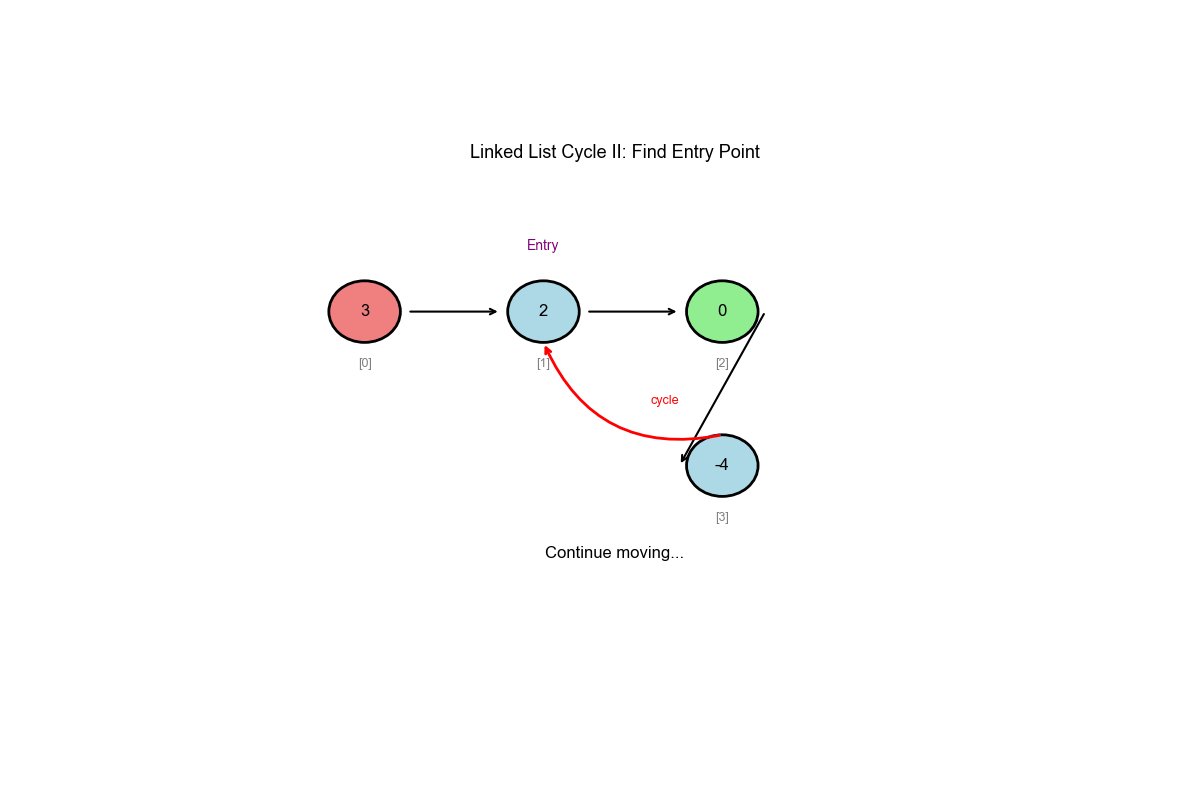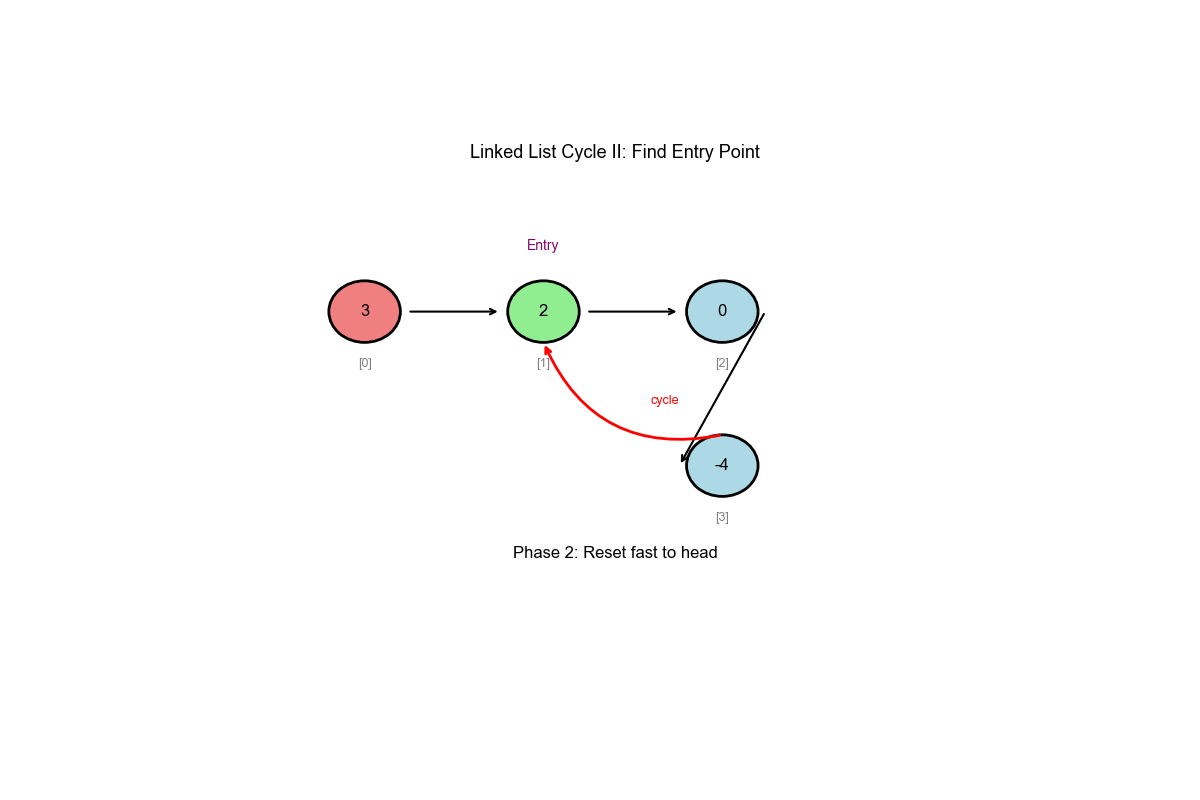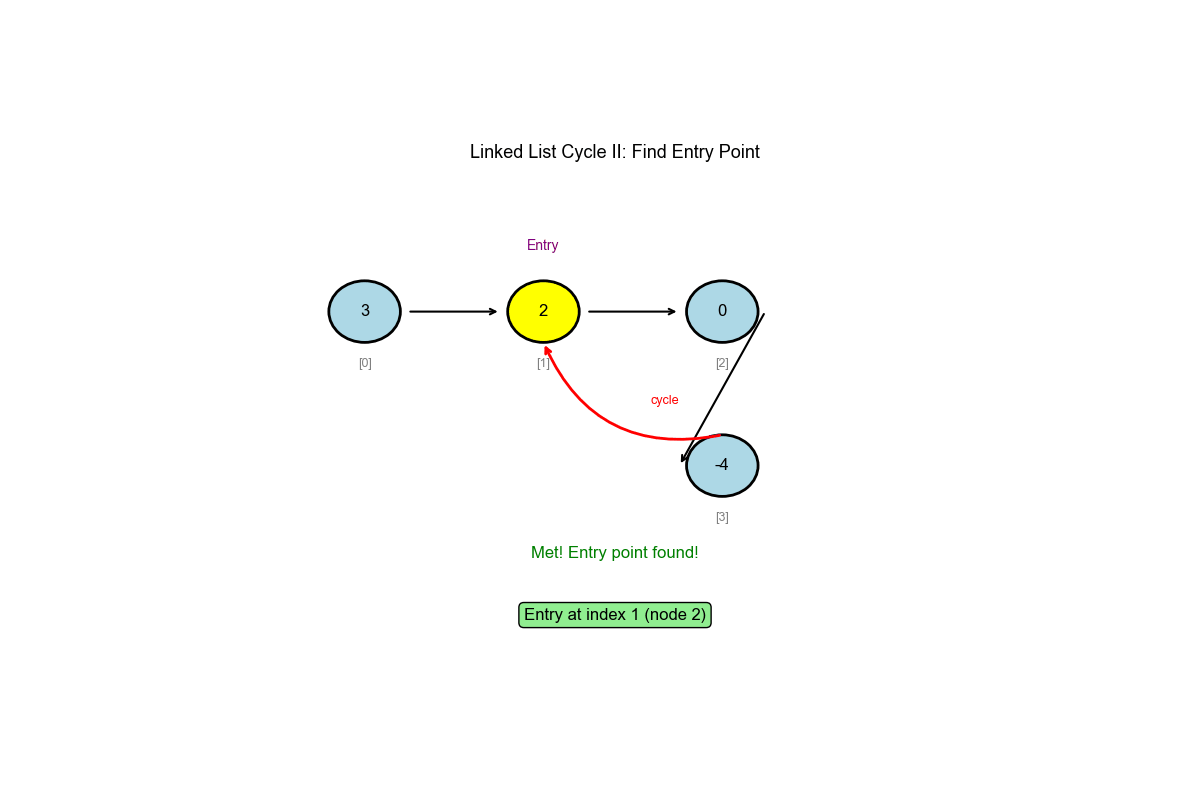
解题思路：使用 Floyd 算法的两阶段方法。阶段一：使用快慢指针检测环并找到相遇点。阶段二：将一个指针移回头部，两个指针以相同速度移动，它们会在环入口相遇。这个方法的正确性基于数学证明：从头部到入口的距离等于从相遇点到入口的距离。

复杂度分析： - 时间复杂度： - 阶段一最多 次迭代，阶段二最多 $ nO(1)$ - 仅使用两个指针

关键洞察： Floyd 算法的数学性质：当快慢指针相遇时，从头部到入口的距离等于从相遇点到入口的距离。这允许我们在 空间内找到入口。

问题描述

给定一个链表的头节点 head，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

进阶：你能用 空间解决吗？

示例：

• 输入：head = [3,2,0,-4]，尾节点连接到索引 1 的节点
• 输出：索引 1 的节点

核心思想： Floyd 环检测算法（扩展）

阶段一：使用快慢指针检测是否存在环

阶段二：找到环入口

1. 相遇后，将一个指针移回起点
2. 两个指针以相同速度移动（每次 1 步）
3. 相遇点就是环入口

Python 实现

def detectCycle(head):
    """
    使用 Floyd 算法找到环开始的节点。
  
    阶段一：使用快/慢指针检测环
    阶段二：通过将一个指针移到起点找到入口
  
    时间复杂度： O(n)
    空间复杂度： O(1)
    """
    if not head or not head.next:
        return None
  
    # 阶段一：检测环
    slow = fast = head
    has_cycle = False
  
    while fast and fast.next:
        slow = slow.next        # 移动 1 步
        fast = fast.next.next   # 移动 2 步
      
        if slow == fast:
            has_cycle = True
            break
  
    if not has_cycle:
        return None
  
    # 阶段二：找到入口
    # 将 slow 移回 head，保持 fast 在相遇点
    # 两者都移动 1 步
    slow = head
    while slow != fast:
        slow = slow.next
        fast = fast.next
  
    return slow  # 这是环入口

数学证明

设：

• 从起点到环入口的距离：

• 从环入口到相遇点的距离：

• 从相遇点回到环入口的距离：

• 环长度： 当它们相遇时：

• 慢指针移动了：

• 快指针移动了：（其中 是额外循环数）

因为快指针是慢指针的 2 倍：

$$

a + b = kL

a = kL - b = (k-1)L + (L - b) = (k-1)L + c $$

关键洞察：从起点走 步到达入口 = 从相遇点走 步到达入口。

因为 是完整循环，从起点和相遇点以相同速度行走将在入口相遇！

可视化解释

起点 → [a 步] → 入口 → [b 步] → 相遇点
                                    ↓
                              [c 步] ←
                                    |
                                    └─── 环（ L = b + c）

当慢指针和快指针相遇时：

• 慢指针：移动了
• 快指针：移动了 （其中 ）

从方程 ：

• 如果我们将 slow 移回起点，两者都以 1 步移动
• Slow 将移动 步到达入口
• Fast 将移动 步，这也到达入口（因为 是完整循环）

复杂度分析

• 时间复杂度：
• 空间复杂度：

常见错误

错误一：不检查环是否存在

# ❌ 错误：假设环存在
slow = fast = head
while slow != fast:  # 如果没有环，这可能永远不会终止！
    slow = slow.next
    fast = fast.next.next

错误二：错误的指针重置

# ❌ 错误：重置 fast 而不是 slow
fast = head  # 应该是 slow = head
while slow != fast:
    # ...

---

LeetCode 160: 相交链表

问题分析

核心难点：如何在 空间内找到两个链表的相交节点。如果两个链表相交，从交点到末尾的路径长度相同，但两个链表在交点之前的长度可能不同。

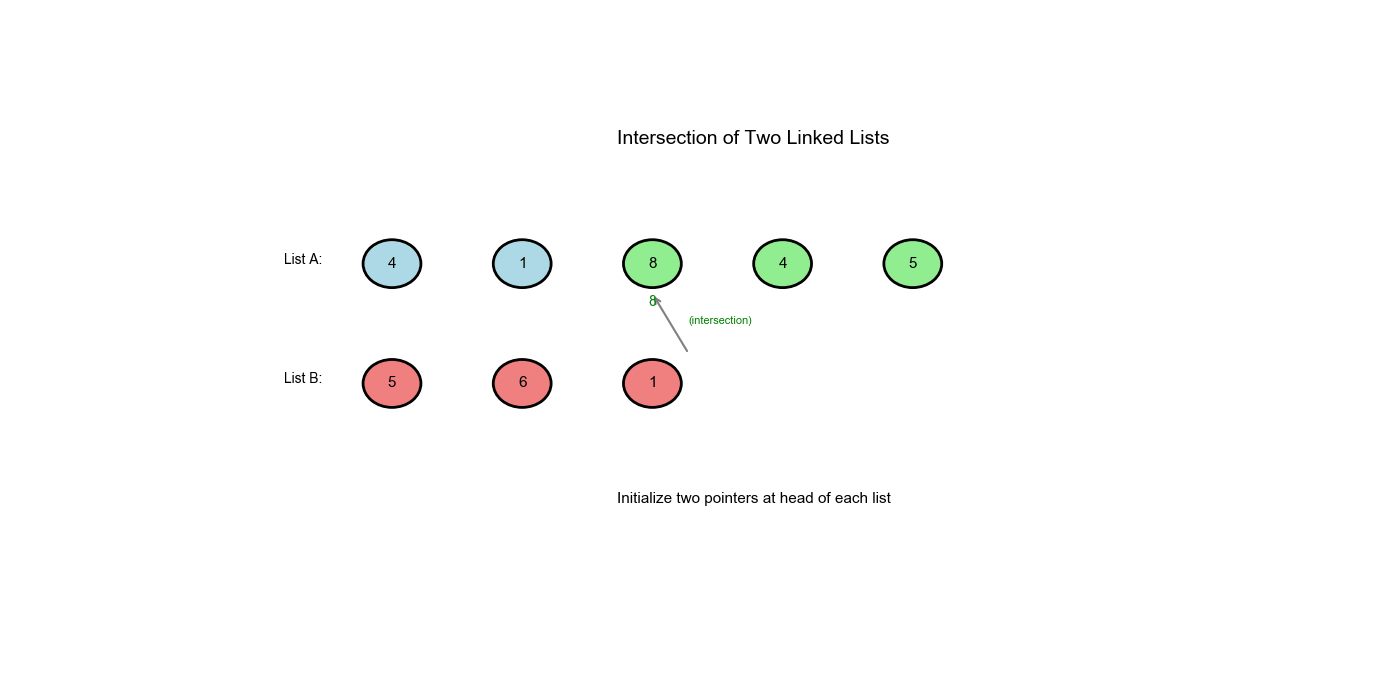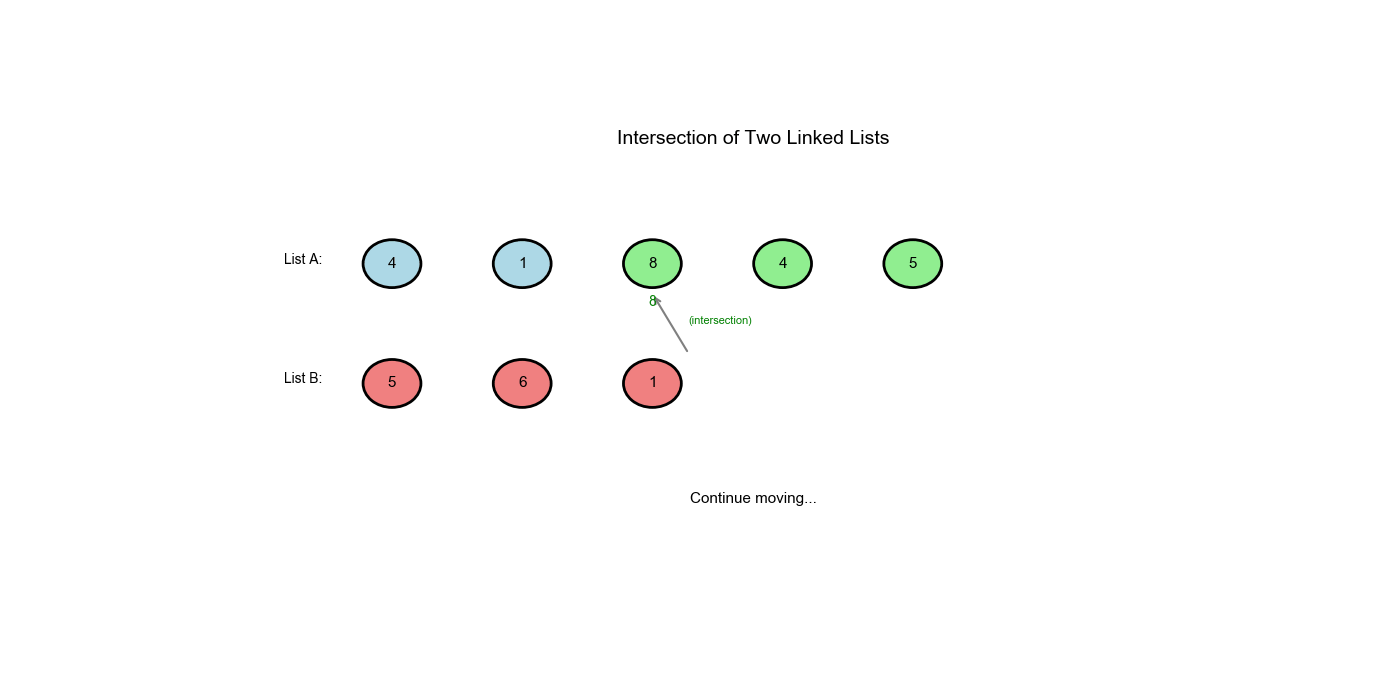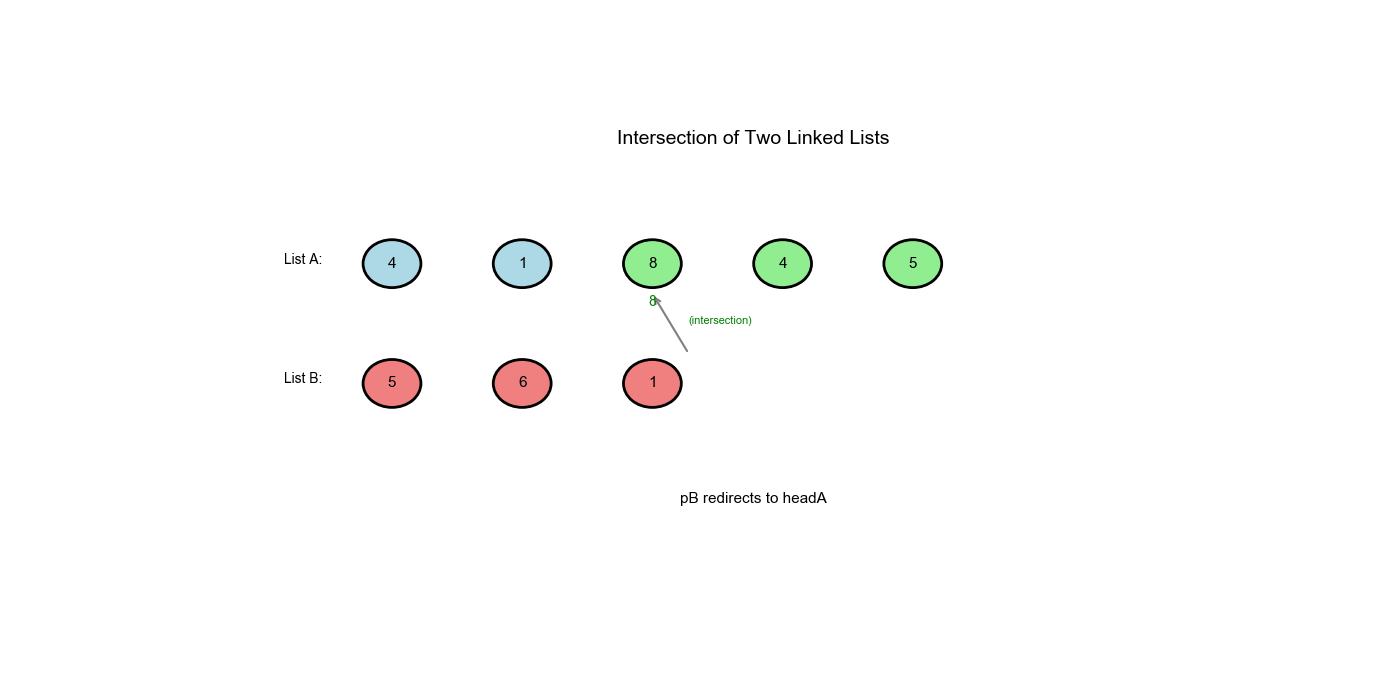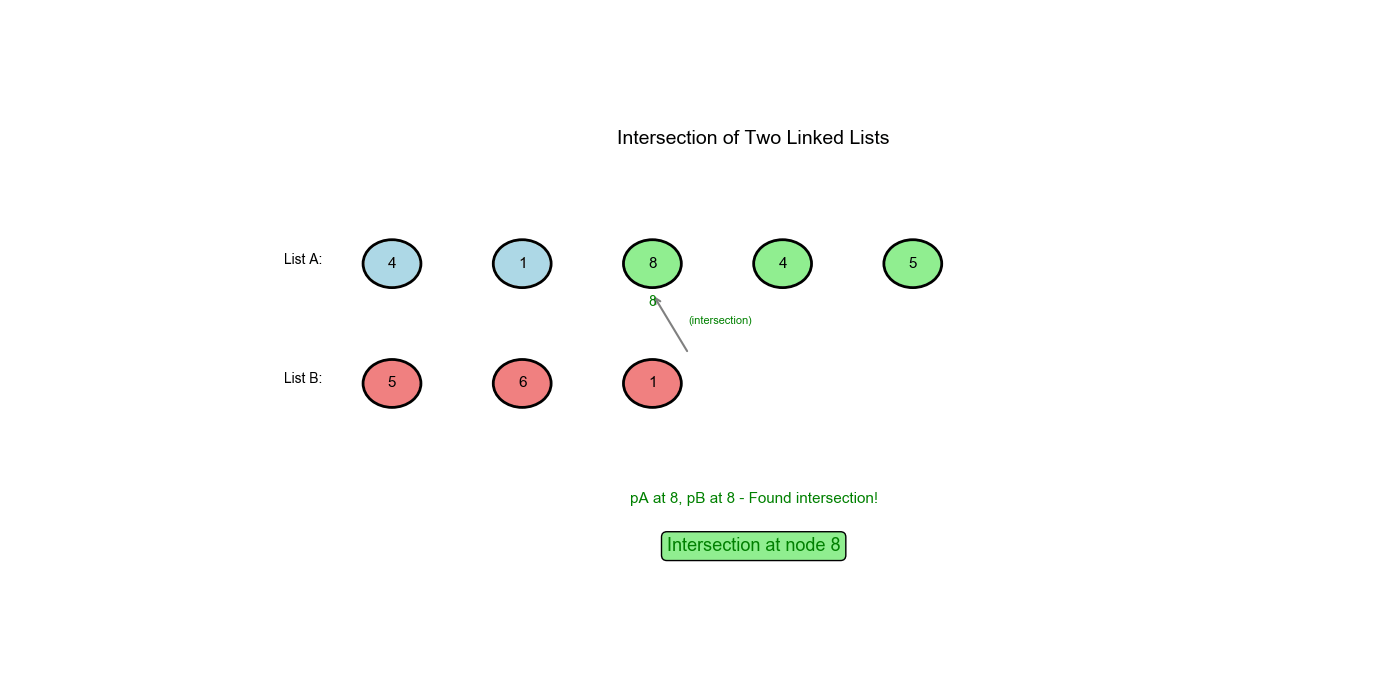
解题思路：使用路径切换的双指针技巧。让指针 pA 遍历链表 A，到达末尾时切换到链表 B 的起点；让指针 pB 遍历链表 B，到达末尾时切换到链表 A 的起点。这样两个指针会走过相同的总距离（ A 的唯一部分 + 公共部分 + B 的唯一部分），如果相交，它们会在交点相遇；如果不相交，它们会同时到达 None。

复杂度分析： - 时间复杂度： - 和 $ nO(1)$ - 仅使用两个指针

关键洞察：路径切换使得两个指针走过相同的总距离，这是找到交点的关键。这个技巧避免了计算链表长度或使用额外空间。

问题描述

给你两个单链表的头节点 headA 和 headB，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null。

约束条件：

• 链表无环
• 函数返回后，链表必须保持其原始结构
• 进阶：时间，空间

示例：

A:     a1 → a2 ↘
                c1 → c2 → c3
B: b1 → b2 → b3 ↗

相交点是 c1。

方法一：双指针（路径对齐）

核心思想

关键观察：如果两个链表相交，从交点到末尾的路径长度相同。

巧妙技巧：

1. 指针 pA 遍历 A，到达末尾时跳到 B 的起点
2. 指针 pB 遍历 B，到达末尾时跳到 A 的起点
3. 两个指针将在交点相遇（或都到达 None）

为什么这样可行？

设：

• A 的唯一部分长度：
• B 的唯一部分长度：
• 公共部分长度：
• pA 路径：
• pB 路径： 它们相等！所以它们会同时到达交点（或 None）。

Python 实现

def getIntersectionNode(headA, headB):
    """
    使用路径切换的双指针找到相交节点。
  
    关键洞察：如果链表相交，切换路径使
    两个指针行进相同的总距离。
  
    时间复杂度： O(m + n)
    空间复杂度： O(1)
    """
    # 边界情况：如果任一链表为空，不可能相交
    if not headA or not headB:
        return None
  
    # 初始化两个指针，分别指向两个链表的头节点
    pA, pB = headA, headB
  
    # 循环直到两指针相遇或都是 None
    # 关键：两个指针都会遍历自己的链表 + 另一个链表
    while pA != pB:
        # 如果 pA 到达链表 A 的末尾（ None）
        # 切换到链表 B 的起点继续遍历
        # 如果 pA 未到达末尾，继续在链表 A 中移动
        pA = pA.next if pA else headB
        
        # 如果 pB 到达链表 B 的末尾（ None）
        # 切换到链表 A 的起点继续遍历
        # 如果 pB 未到达末尾，继续在链表 B 中移动
        pB = pB.next if pB else headA
  
    # 循环结束时， pA 和 pB 要么都是 None（无交点）
    # 要么都指向交点节点（有交点）
    return pA

复杂度分析

• 时间复杂度：
• 空间复杂度：

逐步解析

输入：

A: 1 → 2 → 8 → 9
B: 3 → 8 → 9

步骤	pA	pB	pA == pB?
0	1	3	❌
1	2	8	❌
2	8	9	❌
3	9	None	❌
4	None	1（切换到 A）	❌
5	3（切换到 B）	2	❌
6	8	8	✅相遇！

为什么这样可行：数学证明

设：

• 链表 A 长度：
• 链表 B 长度：
• 其中 $ a b c$= 公共部分

切换后：

• pA 行进：
• pB 行进： 两者行进相同距离！如果它们相交，它们在交点相遇。如果不相交，两者同时变为 None。

---

方法二：哈希集合

Python 实现

def getIntersectionNode_hash(headA, headB):
    """
    使用哈希集合找到交点（更简单但使用 O(m) 空间）。
  
    时间复杂度： O(m + n)
    空间复杂度： O(m) 或 O(n)
    """
    seen = set()
  
    # 遍历 A 并存储所有节点
    curr = headA
    while curr:
        seen.add(curr)
        curr = curr.next
  
    # 遍历 B 并找到集合中的第一个节点
    curr = headB
    while curr:
        if curr in seen:
            return curr
        curr = curr.next
  
    return None

复杂度

• 时间：
• 空间：或 对比：双指针方法是空间最优的！

---

LeetCode 19: 删除链表的倒数第 N 个结点

问题分析

核心难点：如何在一次遍历中找到倒数第 个节点。如果先遍历一次计算长度，再遍历一次删除，需要两次遍历。使用双指针可以在一次遍历中完成。

解题思路：使用双指针保持 的间隔。创建虚拟节点处理删除头节点的边界情况。快指针先移动 步，然后两个指针同步移动，直到快指针到达末尾。此时慢指针位于要删除节点的前一个节点，可以直接删除。关键是要保持 的间隔，而不是 ，这样才能让慢指针停在目标节点的前一个位置。

复杂度分析： - 时间复杂度： - 是链表长度，一次遍历 - 空间复杂度： - 仅使用常数额外指针

关键洞察：双指针的间隔技巧是解决"倒数第 k 个"问题的经典方法。虚拟节点统一处理了删除头节点的特殊情况。

问题描述

给你一个链表，删除链表的倒数第 个结点，并且返回链表的头结点。

进阶：你能尝试使用一趟扫描实现吗？

示例：

• 输入：head = [1,2,3,4,5], n = 2
• 输出：[1,2,3,5]（删除倒数第 2 个节点，即 4）

约束条件：

• 链表中结点的数目为

核心思想：双指针（间隔 n）

步骤：

1. 创建一个虚拟节点（处理删除头节点的情况）
2. 快指针向前移动 步
3. 两个指针同步移动直到快指针到达末尾
4. 慢指针现在位于要删除节点的前一个节点
5. 删除：slow.next = slow.next.next

Python 实现

def removeNthFromEnd(head, n):
    """
    使用双指针删除倒数第 n 个节点。
  
    关键洞察：在快指针和慢指针之间保持 n+1 的间隔。
    当快指针到达末尾时，慢指针在目标节点之前。
  
    时间复杂度： O(L)，其中 L 是链表长度 - 一次遍历！
    空间复杂度： O(1)
    """
    # 创建虚拟节点处理删除头节点的边界情况
    # 如果删除的是头节点， dummy.next 会指向新的头节点
    dummy = ListNode(0)
    dummy.next = head
  
    # 初始化快慢指针都指向虚拟节点
    fast = slow = dummy
  
    # 关键：将快指针向前移动 n+1 步
    # 为什么是 n+1？因为需要慢指针停在目标节点的前一个位置
    # 如果移动 n 步，慢指针会停在目标节点本身，无法删除
    for _ in range(n + 1):
        fast = fast.next
  
    # 同步移动两个指针，直到快指针到达末尾（ None）
    # 此时慢指针和目标节点之间保持 n+1 的间隔
    while fast:
        fast = fast.next  # 快指针移动
        slow = slow.next  # 慢指针移动
  
    # 现在 slow 指向目标节点的前一个节点
    # 删除目标节点：跳过目标节点，直接连接到目标节点的下一个节点
    slow.next = slow.next.next
  
    # 返回 dummy.next（跳过虚拟节点）
    return dummy.next

复杂度分析

• 时间复杂度：，其中 是链表长度，一次遍历
• 空间复杂度：

深入解读

算法原理：为什么双指针间隔技巧能 work？

核心思想：要删除倒数第 个节点，需要找到它的前一个节点。如果我们让快指针先移动 步，然后两个指针同步移动，当快指针到达末尾时，慢指针正好在目标节点的前一个位置。

数学证明：设链表长度为 ，要删除倒数第 个节点（即正数第 个节点）。 - 目标节点的前一个节点是第 个节点 - 快指针移动 步后，距离慢指针 - 当快指针到达末尾（移动 步）时，慢指针移动了 步 - 从虚拟节点开始，慢指针指向第 个节点 ✅

时间复杂度证明：为什么是 O(L)？

• 快指针移动：先移动 步，然后移动 步到达末尾
• 总移动：步
• 慢指针移动：步
• 总时间：

空间优化：有没有更省空间的方法？

这个问题已经是空间最优的： - 虚拟节点：空间（一个节点） - 双指针：空间（两个指针） - 无法进一步优化：必须跟踪指针位置

对比其他方法： | 方法 | 时间 | 空间 | 遍历次数 | |------|------|------|---------| | 双指针 | | | 1 次 | | 先计算长度 | | | 2 次 | | 使用栈 | | | 1 次 |

常见错误分析

错误类型	错误代码	问题	正确做法
间隔错误	for _ in range(n)	慢指针停在目标节点	range(n + 1)
不使用虚拟节点	直接处理头节点	需要特殊处理	使用 dummy
忘记检查边界	不检查 n 是否有效	可能越界	先验证 n

变体扩展

1. 删除链表的倒数第 N 个结点（一次遍历）：当前方法
2. 找到链表的中间节点：快指针移动 2 步，慢指针移动 1 步
3. 找到链表的第 k 个节点：快指针先移动 k 步

为什么快指针移动 n+1 步？

目标：使 slow 停在目标节点的前一个节点。

示例：head = [1,2,3,4,5], n = 2（删除 4）

快指针位置	慢指针位置	解释
dummy → 1 → 2 → 3	dummy	快指针移动了 3 步（ n+1）
3 → 4 → 5 → None	dummy → 1 → 2 → 3	同步移动
None	3	Slow 在 3，可以删除 4

边界情况：删除头节点

输入：head = [1,2], n = 2（删除 1）

• 快指针移动 3 步：dummy → 1 → 2 → None
• 慢指针仍在 dummy
• 删除：dummy.next = 1.next = 2
• 返回：dummy.next = 2 ✅

不使用虚拟节点：需要特殊处理头删除，代码变得复杂！

常见错误

错误一：错误的间隔大小

# ❌ 错误：仅 n 步， slow 将在目标节点，而不是之前
for _ in range(n):
    fast = fast.next
# 现在 slow.next = slow.next.next 将删除错误的节点

错误二：不使用虚拟节点

# ❌ 错误：需要头删除的特殊情况
if n == length:
    return head.next
# 更复杂的代码...

---

LeetCode 23: 合并 K 个有序链表

问题描述

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例：

• 输入：lists = [[1,4,5],[1,3,4],[2,6]]
• 输出：[1,1,2,3,4,4,5,6]

约束条件：

• 

方法一：分治

核心思想

递归地成对合并链表，类似于归并排序：

1. 分：将链表数组分成两半
2. 治：递归合并每一半
3. 合：合并两个合并后的半部分

Python 实现

def mergeKLists(lists):
    """
    使用分治合并 k 个有序链表。
  
    时间复杂度： O(n log k)，其中 n 是总节点数， k 是链表数
    空间复杂度： O(log k) 用于递归栈
    """
    if not lists:
        return None
    if len(lists) == 1:
        return lists[0]
  
    mid = len(lists) // 2
    left = mergeKLists(lists[:mid])
    right = mergeKLists(lists[mid:])
  
    return mergeTwoLists(left, right)  # 使用我们之前的合并函数

def mergeTwoLists(l1, l2):
    """问题二的辅助函数"""
    dummy = ListNode(-1)
    current = dummy
  
    while l1 and l2:
        if l1.val <= l2.val:
            current.next = l1
            l1 = l1.next
        else:
            current.next = l2
            l2 = l2.next
        current = current.next
  
    current.next = l1 if l1 else l2
    return dummy.next

复杂度分析

• 时间复杂度：，其中 $ n k$是链表数
• 空间复杂度：，递归栈深度

为什么分治？

朴素方法：逐个合并链表

• 时间：（每次合并是 ，执行 次）

分治：成对合并

• 时间：（合并树有 层，每层处理 个节点）

---

方法二：优先队列（堆）

Python 实现

import heapq

def mergeKLists_heap(lists):
    """
    使用最小堆合并 k 个有序链表。
  
    时间复杂度： O(n log k)
    空间复杂度： O(k) 用于堆
    """
    # 最小堆总是获取最小元素
    heap = []
  
    # 用每个链表的第一个节点初始化堆
    for i, node in enumerate(lists):
        if node:
            heapq.heappush(heap, (node.val, i, node))
  
    dummy = ListNode(-1)
    current = dummy
  
    while heap:
        val, idx, node = heapq.heappop(heap)
        current.next = node
        current = current.next
      
        # 如果同一链表有下一个节点，添加到堆
        if node.next:
            heapq.heappush(heap, (node.next.val, idx, node.next))
  
    return dummy.next

---

LeetCode 138: 复制带随机指针的链表

问题描述

给你一个长度为 的链表，每个节点包含一个额外增加的随机指针 random，该指针可以指向链表中的任何节点或空节点。

构造这个链表的深拷贝。

示例：

原始： 7 → 13 → 11 → 10 → 1 → None
      ↓    ↓     ↓     ↓    ↓

      -    7     1     11   7

方法：两次遍历与哈希映射

核心思想

1. 第一次遍历：创建所有新节点并建立旧 → 新映射
2. 第二次遍历：使用映射连接 next 和 random 指针

Python 实现

def copyRandomList(head):
    """
    深拷贝带随机指针的链表。
  
    两次遍历方法：
    1. 创建所有节点并建立旧→新映射
    2. 使用映射连接 next 和 random 指针
  
    时间复杂度： O(n)
    空间复杂度： O(n) 用于哈希映射
    """
    if not head:
        return None
  
    # 映射旧节点到新节点
    node_map = {}
  
    # 第一次遍历：创建所有节点
    curr = head
    while curr:
        node_map[curr] = Node(curr.val)
        curr = curr.next
  
    # 第二次遍历：连接指针
    curr = head
    while curr:
        new_node = node_map[curr]
        # 连接 next 指针
        if curr.next:
            new_node.next = node_map[curr.next]
        # 连接 random 指针
        if curr.random:
            new_node.random = node_map[curr.random]
        curr = curr.next
  
    return node_map[head]

复杂度分析

• 时间复杂度：，两次遍历
• 空间复杂度：，哈希映射存储

---

虚拟节点的威力

何时使用虚拟节点？

信号：

• 可能删除头节点
• 需要返回新头节点
• 构建新链表

好处：

• 统一处理头节点和其他节点
• 无空链表的特殊情况
• 代码更简洁

对比示例：删除节点

不使用虚拟节点：

def deleteNode(head, val):
    # ❌ 头节点的特殊情况
    if head.val == val:
        return head.next
  
    curr = head
    while curr.next:
        if curr.next.val == val:
            curr.next = curr.next.next
            break
        curr = curr.next
    return head

使用虚拟节点：

def deleteNode_dummy(head, val):
    dummy = ListNode(0)
    dummy.next = head
    curr = dummy
  
    # ✅ 统一处理
    while curr.next:
        if curr.next.val == val:
            curr.next = curr.next.next
            break
        curr = curr.next
  
    return dummy.next

---

常见陷阱与调试技巧

陷阱一：空指针访问

# ❌ curr 可能是 None
while curr:
    if curr.next.val == target:  # 💥 curr.next 可能是 None
        # ...

修复：

# ✅ 检查 curr.next 是否存在
while curr and curr.next:
    if curr.next.val == target:
        # ...

陷阱二：修改指针后丢失节点引用

# ❌ 错误示例
curr.next = curr.next.next  # 直接跳过，丢失对删除节点的引用

正确方法：

• 如果需要访问删除的节点，先保存：

  to_delete = curr.next
  curr.next = curr.next.next
  # 仍可使用 to_delete

陷阱三：忘记移动指针

# ❌ 无限循环
while curr:
    # 处理逻辑
    # 忘记： curr = curr.next

调试技巧

技巧一：打印链表

def print_list(head):
    vals = []
    curr = head
    while curr:
        vals.append(str(curr.val))
        curr = curr.next
    print(" → ".join(vals) + " → None")

技巧二：画图

在每一步绘制链表状态，特别是在修改指针时。

技巧三：逐步调试

对于复杂操作（如反转、合并），逐步执行并检查每一步后的指针状态。

---

链表面试沟通模板

模板一：识别链表特征

"这个问题涉及链表操作。链表具有插入/删除但 访问。我将使用[迭代/递归]方法，采用[双指针/虚拟节点]技术来[反转/合并/检测]链表。"

模板二：选择迭代 vs 递归

"我可以用迭代实现，空间复杂度 ，或者用递归实现，代码更简洁但空间复杂度 。对于生产环境，我倾向于迭代以避免栈溢出；对于面试，我先展示迭代，然后提及递归作为替代。"

模板三：解释虚拟节点

"我将使用虚拟节点作为哨兵来统一处理头节点特殊情况，避免复杂的边界检查。最后，返回 dummy.next。"

模板四：快慢指针

"我将使用快慢指针：快指针移动 2 步，慢指针移动 1 步。这以一次遍历解决，时间复杂度 ，空间复杂度 。"

---

❓ Q&A：链表面试技巧

Q1：什么时候应该对链表使用递归 vs 迭代？

答案：当以下情况使用迭代：

• 空间优化重要（ vs ）
• 生产代码（避免栈溢出风险）
• 长链表（递归深度担忧）

当以下情况使用递归：

• 代码清晰度优先
• 在面试中展示多种方法
• 自然递归结构（例如，类似树的问题）

面试提示：总是提及两种方法，但先实现迭代。

---

Q2：如何系统地处理边界情况？

答案：系统地检查这些：

1. 空链表：head == None
2. 单节点：head.next == None
3. 两节点：操作的特殊情况
4. 头节点修改：使用虚拟节点
5. 环检测：访问前检查 fast 和 fast.next

模式：访问 node.next 前总是检查 node。

---

Q3：找链表中间的最佳方法是什么？

答案：使用快慢指针：

def findMiddle(head):
    slow = fast = head
    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next
    return slow

当快指针到达末尾时，慢指针在中点（或偶数长度时的第二个中点）。

---

Q4：如何在不使用额外空间的情况下检测环？

答案：使用Floyd 算法（快慢指针）：

• 快指针移动 2 步，慢指针移动 1 步
• 如果它们相遇，存在环
• 找入口：将一个指针移到起点，两者都移动 1 步

时间：，空间：

Q5：当你只能访问该节点时，删除节点的技巧是什么？

答案：复制下一个节点的数据，然后删除下一个节点：

def deleteNode(node):
    # 如果是最后一个节点，无法删除
    if not node.next:
        return
  
    # 复制下一个节点的值
    node.val = node.next.val
    # 删除下一个节点
    node.next = node.next.next

注意：这对最后一个节点不起作用（需要 None）。

---

Q6：如何按 k 组反转链表？

答案：使用递归：

def reverseKGroup(head, k):
    # 检查是否有 k 个节点
    curr = head
    count = 0
    while curr and count < k:
        curr = curr.next
        count += 1
  
    if count == k:
        # 反转前 k 个节点
        curr = reverseKGroup(curr, k)  # 递归处理剩余部分
        while count > 0:
            next_node = head.next
            head.next = curr
            curr = head
            head = next_node
            count -= 1
        head = curr
    return head

---

Q7：链表问题中最常见的错误是什么？

答案：当 node 可能是 None 时访问 node.next。

总是检查：

if node and node.next:
    # 安全访问 node.next

---

Q8：如何高效合并 k 个有序链表？

答案：两种主要方法：

1. 分治：时间，空间

   • 递归成对合并

2. 优先队列：时间，空间

   • 使用最小堆总是获取最小元素

两者都是最优的。根据空间约束选择。

---

Q9：能否在不使用额外空间的情况下原地修改链表？

答案：可以！大多数操作可以在 空间中完成：

• 反转：三指针
• 环检测：快慢指针
• 合并：虚拟节点 + 指针
• 删除：双指针

关键：巧妙地使用指针，避免额外数据结构。

---

Q10：被问及时间/空间复杂度时应该说什么？

答案：要具体：

• 时间：计算操作（遍历、比较）
• 空间：计算额外变量（指针 = ，递归栈 = ，哈希映射 = ）

示例："这使用两个指针，所以空间是 。我们遍历一次，所以时间是 。"

---

练习题目（ 10 道推荐）

基本操作

1. 反转链表（ LeetCode 206）← 本文已覆盖 简单
2. 合并两个有序链表（ LeetCode 21）← 本文已覆盖 简单
3. 删除链表的倒数第 N 个结点（ LeetCode 19）← 本文已覆盖 中等

环检测与相交

4. 环形链表（ LeetCode 141）简单
5. 环形链表 II（ LeetCode 142）← 本文已覆盖 中等
6. 相交链表（ LeetCode 160）← 本文已覆盖 简单

高级操作

7. 回文链表（ LeetCode 234）简单
8. 排序链表（ LeetCode 148）中等
9. 重排链表（ LeetCode 143）中等
10. 复制带随机指针的链表（ LeetCode 138）← 本文已覆盖 中等

---

总结：链表操作速查表

核心技术快速参考

技术	用例	示例问题
双指针	找中点、环检测、倒数第 n 个	环检测、删除倒数第 n 个节点
虚拟节点	删除头节点、构建新链表	合并链表、删除节点
递归	反转、合并（代码简洁）	反转链表、合并链表
迭代	所有操作（空间最优）	反转链表、检测环

何时使用什么？

双指针：

• 需要同时跟踪多个位置
• 环检测（快慢）
• 找中点、倒数第 n 个

虚拟节点：

• 可能修改头节点
• 构建新链表
• 简化边界条件

递归 vs 迭代：

• 递归：代码简洁，适合展示算法思维
• 迭代：空间最优，更适合生产环境

常见陷阱

1. 空指针：访问 node.next 前检查 node
2. 丢失引用：修改指针前保存必要引用
3. 忘记移动指针：每个循环分支必须移动指针
4. 边界情况：空链表、单节点、头节点操作

面试黄金短语

"链表的核心是指针操作。我将使用[双指针/虚拟/递归]技术，确保边界安全，实现时间，空间（或解释递归的 栈空间）。"

记忆口诀

双指针找环和中点，虚拟简化边界，迭代节省空间递归优雅，指针操作避免空指针和陷阱！

---

下一篇文章预览

在LeetCode（四）：二叉树遍历与递归中，我们将探索：

• 四种遍历方法：前序、中序、后序、层序
• 递归模式：子树问题分解
• Morris 遍历：空间遍历
• 经典问题：最近公共祖先、路径和、树序列化

思考题：如何在不使用递归或栈的情况下执行中序遍历？下一篇文章见答案！

---

链表不是数据结构的"困难部分"——它们是指针思维的试金石。掌握它们，你将轻松处理树、图和更复杂的结构！