推荐系统（二）—— 协同过滤与矩阵分解
Chen Kai BOSS
  2024-05-07 14:30:00 2024-05-07 14:30      11.3k 字  51 分钟  

想象一下：你刚看完《肖申克的救赎》，想找一部类似的电影。传统方法可能是按类型、导演、演员来筛选，但协同过滤（ Collaborative Filtering）走的是另一条路——它不关心电影本身的属性，而是观察"和你品味相似的用户也喜欢什么"。如果用户 A 和用户 B 都喜欢《肖申克的救赎》和《阿甘正传》，而用户 A 还喜欢《当幸福来敲门》，那么系统就会向用户 B 推荐这部电影。

协同过滤是推荐系统的基石，从 1990 年代的 GroupLens 系统到 Netflix Prize 竞赛，再到今天各大平台的个性化推荐，都离不开它。而矩阵分解（ Matrix Factorization）则是协同过滤的数学核心，它将用户-物品评分矩阵分解为低维向量，用向量内积预测评分，既解决了数据稀疏性问题，又为深度学习推荐系统奠定了基础。

本文深入讲解协同过滤的两种范式（ User-CF 和 Item-CF）、相似度计算方法、矩阵分解的数学原理、 SVD/SVD++ 算法、 ALS 优化方法、 BPR 排序学习、 FM 因子分解机、隐式反馈处理、偏置项设计，并提供完整的 Python 实现代码。每个算法都配有详细的数学推导、代码示例和 Q&A 解答，帮助你从理论到实践全面掌握推荐系统的核心算法。

协同过滤的基本思想

什么是协同过滤？

协同过滤（ Collaborative Filtering， CF）的核心假设是：相似的用户会有相似的偏好，相似的物品会被相似的用户喜欢。它不需要知道物品的内容特征（如电影的类型、演员），也不需要知道用户的画像（如年龄、性别），只需要利用用户的历史行为数据（评分、点击、购买等）就能做出推荐。

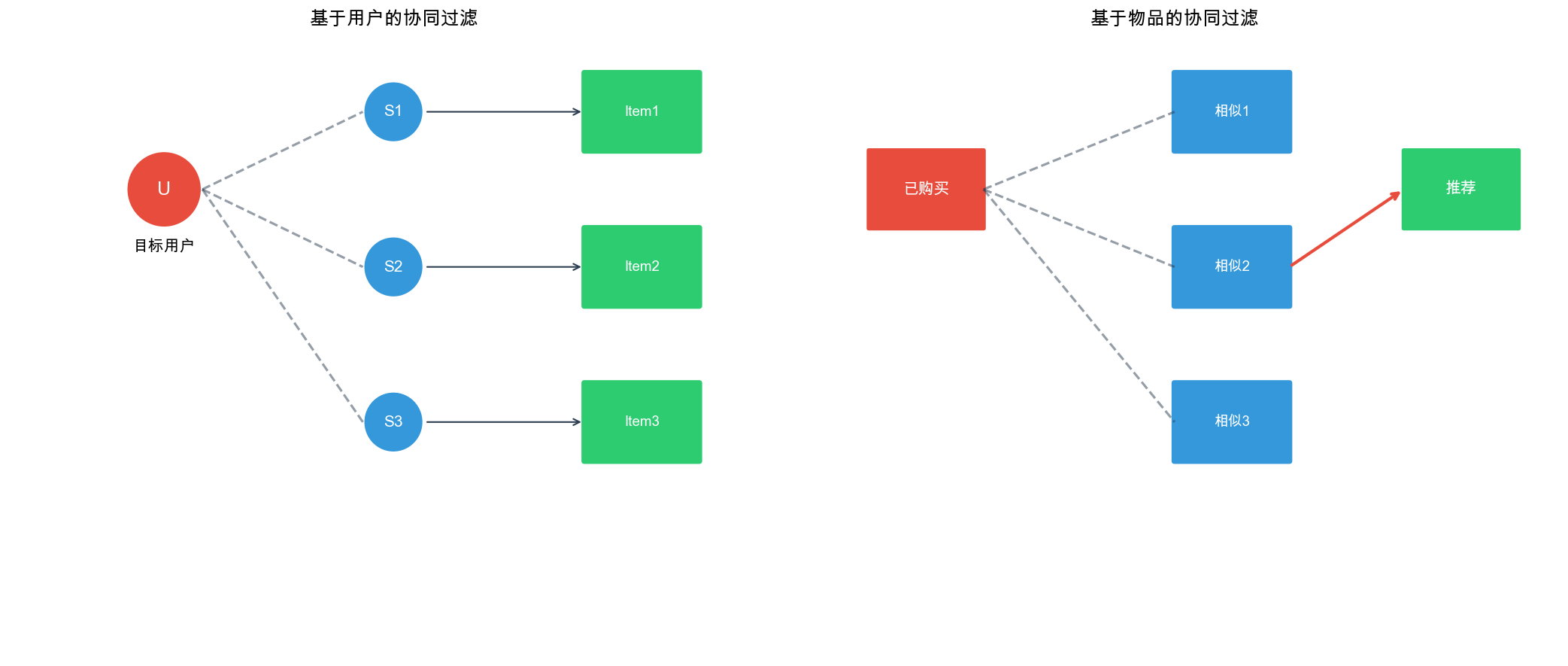
协同过滤分为两大类：

  1. 基于用户的协同过滤（ User-Based CF）：找到与目标用户相似的用户，推荐这些相似用户喜欢的物品。
  2. 基于物品的协同过滤（ Item-Based CF）：找到与目标物品相似的物品，如果用户喜欢某个物品，就推荐相似的物品。

一个直观的例子

假设我们有 5 个用户对 5 部电影的评分矩阵（ 1-5 分）：

用户 肖申克 阿甘 当幸福 泰坦尼克 教父
Alice 5 5 ? 3 4
Bob 5 5 4 2 ?
Carol 4 4 3 5 5
David 2 1 ? 4 3
Eve ? ? 2 3 4

User-CF 的思路： Alice 和 Bob 都对《肖申克的救赎》和《阿甘正传》打了高分，说明他们品味相似。 Bob 给《当幸福来敲门》打了 4 分，所以向 Alice 推荐这部电影。

Item-CF 的思路：《肖申克的救赎》和《阿甘正传》被 Alice 、 Bob 、 Carol 都打了高分，说明这两部电影相似。如果用户喜欢《肖申克的救赎》，就推荐《阿甘正传》。

协同过滤的优势与局限

优势： - 无需内容特征：不需要知道电影的类型、演员等信息 - 能发现意外关联：可能发现"买尿布的也买啤酒"这种非直观关联 - 跨领域推荐：可以推荐不同类别的物品

局限： - 冷启动问题：新用户或新物品没有历史数据 - 数据稀疏性：用户-物品矩阵通常非常稀疏（ 99% 以上是缺失值） - 可扩展性：用户和物品数量增长时，计算相似度成本高 - 流行度偏差：热门物品容易被推荐，长尾物品被忽略

基于用户的协同过滤（ User-CF）

算法流程

User-CF 的核心步骤：

  1. 计算用户相似度：找到与目标用户 最相似的 个用户（称为"邻居"）
  2. 预测评分：基于这 个邻居对物品 的评分，预测用户 对物品 的评分
  3. 生成推荐：选择预测评分最高的 个物品推荐给用户

相似度计算方法

相似度衡量两个用户评分向量的接近程度。设用户 和 对物品集合 （两个用户都评过分的物品）的评分向量分别为 和 。

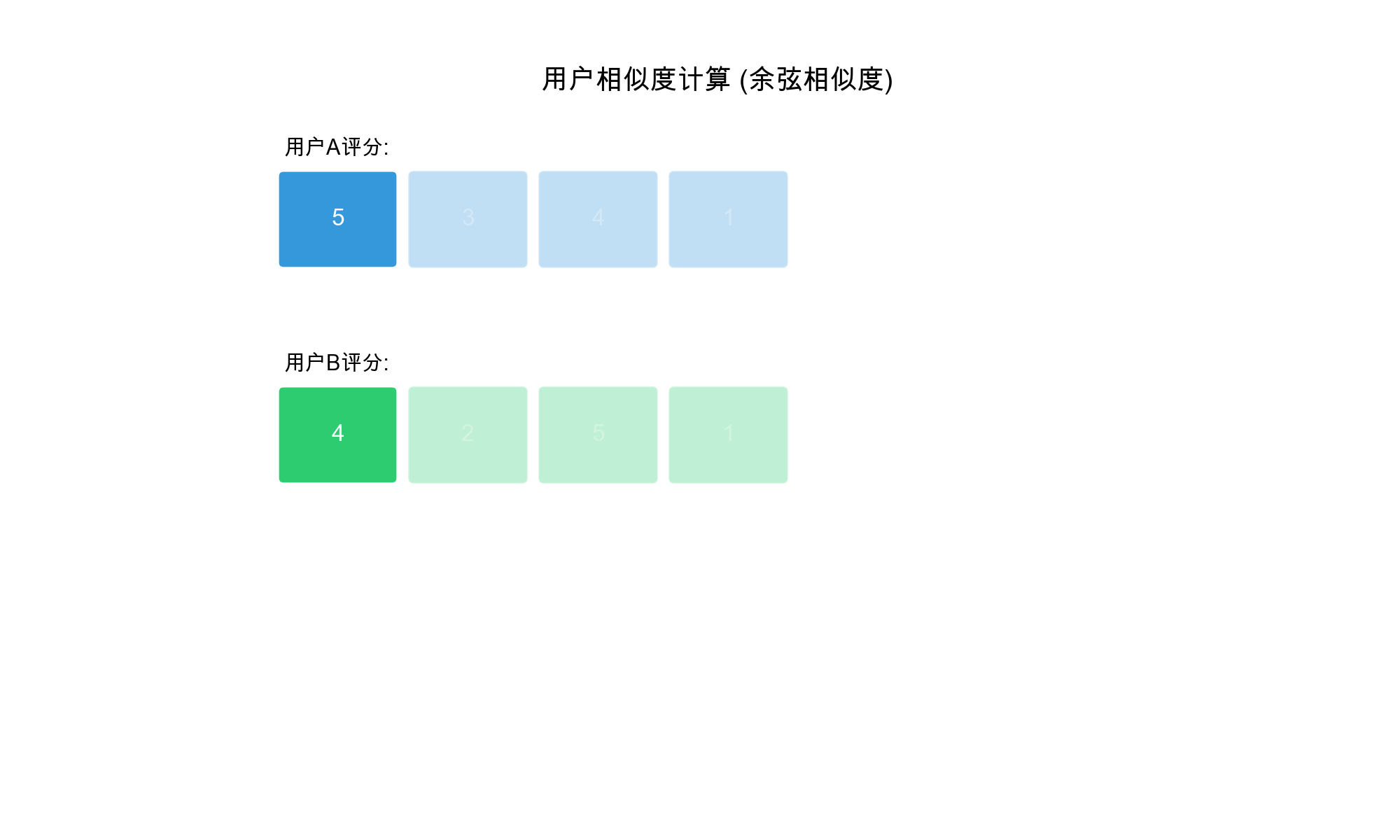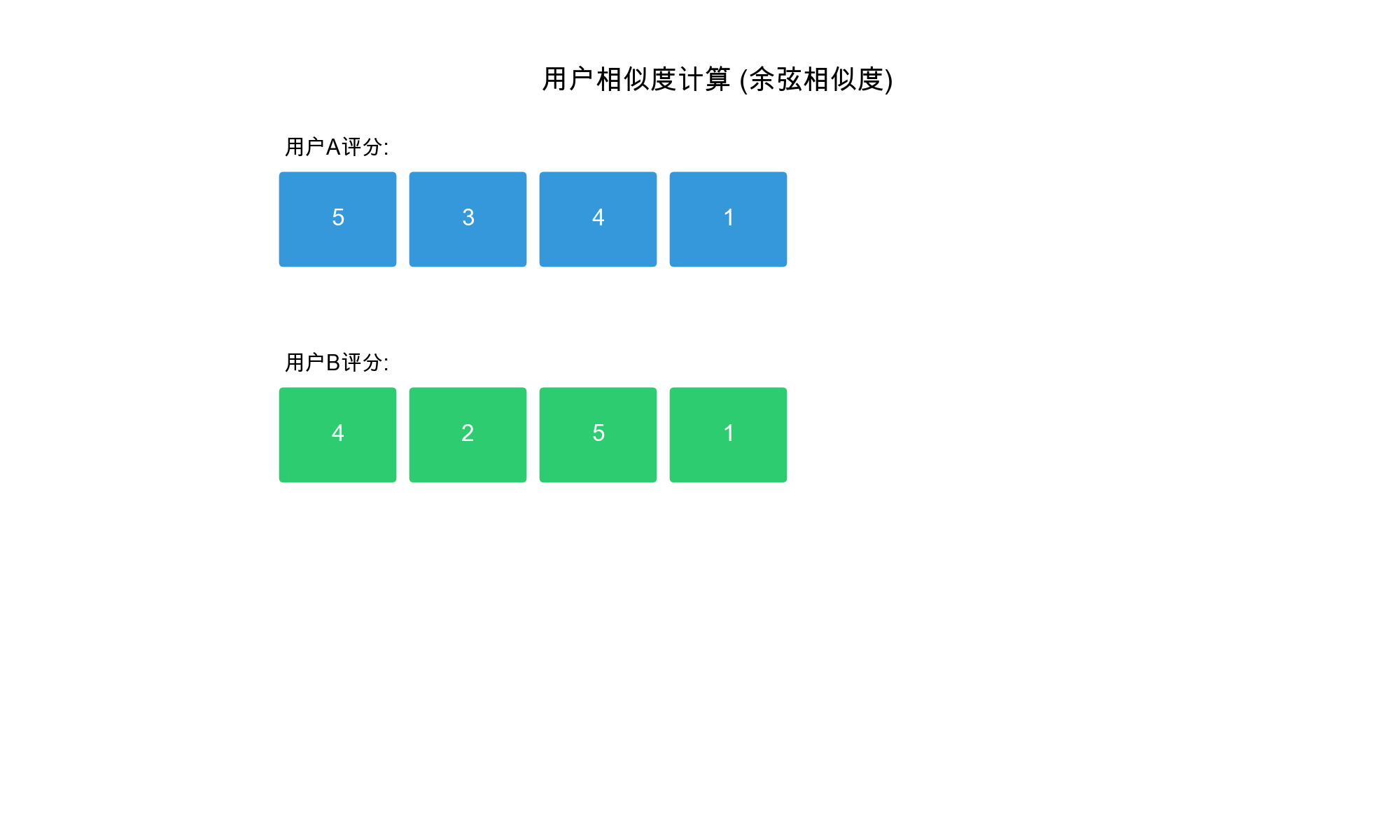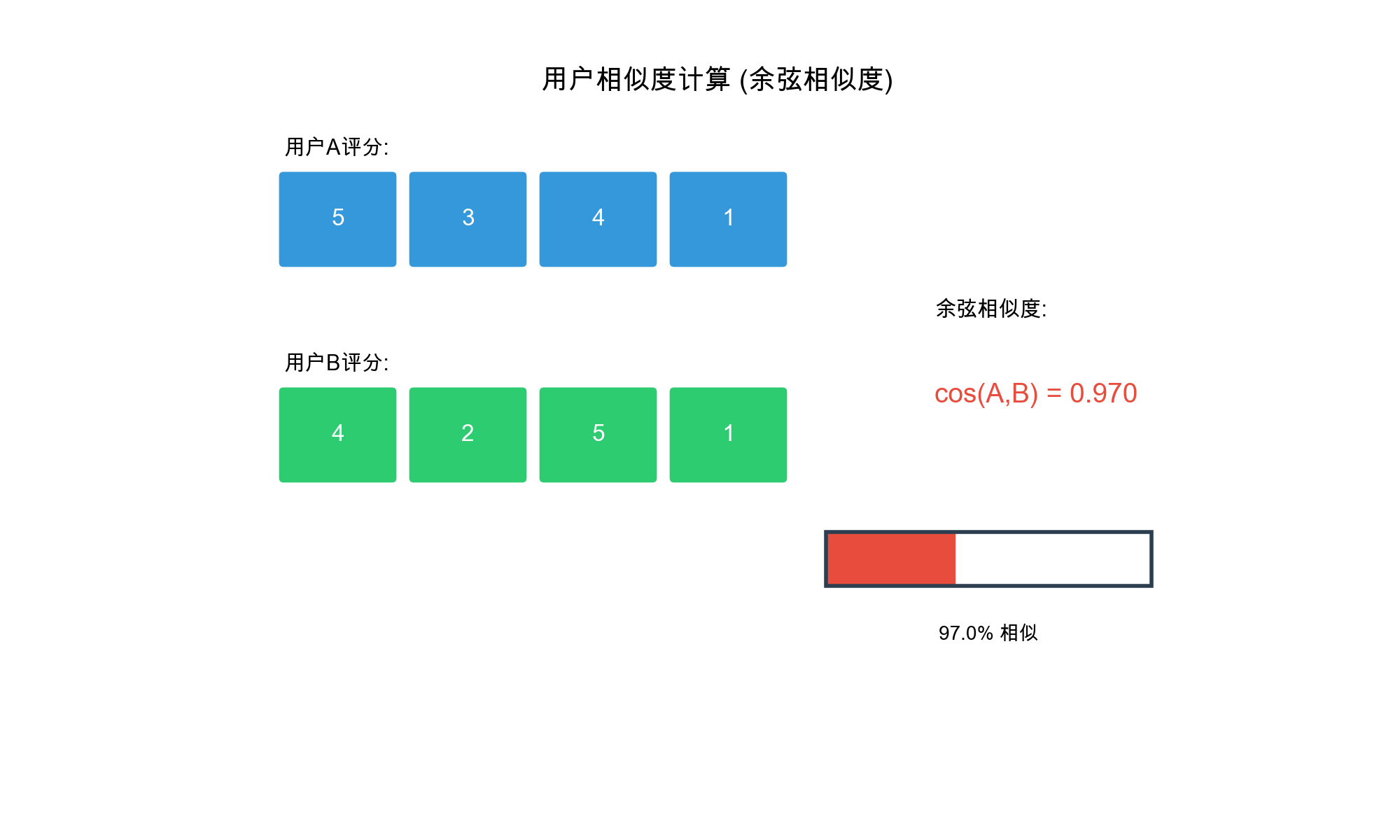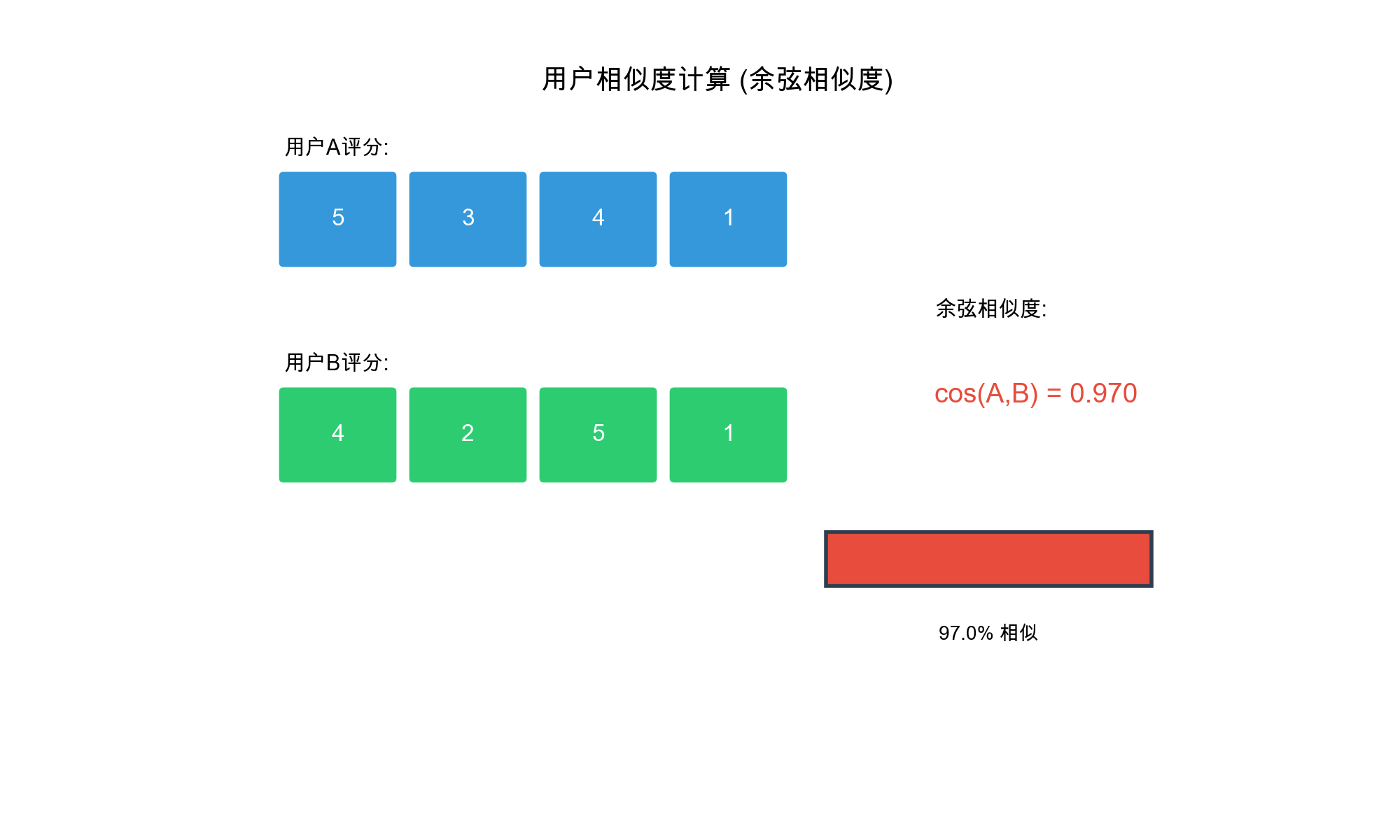
1. 余弦相似度（ Cosine Similarity）

将用户评分看作向量，计算向量夹角的余弦值：

余弦相似度的取值范围是 ，值越大表示越相似。

特点： - 只考虑评分的方向（偏好），不考虑评分的绝对值 - 对评分尺度不敏感 - 适合评分范围不同的场景

2. 皮尔逊相关系数（ Pearson Correlation）

考虑用户评分均值的差异，计算标准化后的相关系数：

其中 是用户 的平均评分。

特点： - 考虑了用户的评分习惯（有些用户习惯打高分，有些习惯打低分） - 取值范围 - 比余弦相似度更常用

3. 调整余弦相似度（ Adjusted Cosine）

在余弦相似度的基础上减去用户平均评分：

实际上，调整余弦相似度与皮尔逊相关系数在数学上等价。

4. 欧氏距离（ Euclidean Distance）

计算评分向量的欧氏距离，然后转换为相似度：

$$

d(u, v) = (u, v) = $$

特点： - 距离越小，相似度越高 - 对异常值敏感

评分预测公式

找到 个最相似用户后，预测用户 对物品 的评分：

其中： - 是用户 的平均评分 - 是与用户 最相似的 个用户集合 - 是用户 和 的相似度 - 是用户 对物品 的评分相对于其平均评分的偏差

公式解释： - 基础分是用户 的平均评分 - 加权平均相似用户对物品 的评分偏差 - 权重是相似度，相似度越高，影响越大

User-CF 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
import numpy as np
from collections import defaultdict
from scipy.spatial.distance import cosine
from scipy.stats import pearsonr

class UserBasedCF:
    def __init__(self, k=20, similarity='pearson'):
        """
        User-Based Collaborative Filtering
        
        Parameters:
        -----------
        k : int
            邻居数量
        similarity : str
            相似度计算方法：'cosine', 'pearson', 'euclidean'
        """
        self.k = k
        self.similarity = similarity
        self.user_item_matrix = None
        self.user_means = None
        self.similarity_matrix = None
        
    def fit(self, user_item_matrix):
        """
        训练模型
        
        Parameters:
        -----------
        user_item_matrix : dict
            {user_id: {item_id: rating }}
        """
        self.user_item_matrix = user_item_matrix
        self.user_means = {}
        
        # 计算每个用户的平均评分
        for user_id, items in user_item_matrix.items():
            ratings = list(items.values())
            self.user_means[user_id] = np.mean(ratings) if ratings else 0
        
        # 计算用户相似度矩阵
        self._compute_similarity_matrix()
    
    def _compute_similarity_matrix(self):
        """计算用户相似度矩阵"""
        users = list(self.user_item_matrix.keys())
        n_users = len(users)
        self.similarity_matrix = np.zeros((n_users, n_users))
        self.user_to_idx = {user: idx for idx, user in enumerate(users)}
        self.idx_to_user = {idx: user for idx, user in enumerate(users)}
        
        for i in range(n_users):
            for j in range(i + 1, n_users):
                sim = self._compute_similarity(users[i], users[j])
                self.similarity_matrix[i][j] = sim
                self.similarity_matrix[j][i] = sim
    
    def _compute_similarity(self, user1, user2):
        """计算两个用户的相似度"""
        items1 = set(self.user_item_matrix[user1].keys())
        items2 = set(self.user_item_matrix[user2].keys())
        common_items = items1 & items2
        
        if len(common_items) == 0:
            return 0
        
        ratings1 = [self.user_item_matrix[user1][item] for item in common_items]
        ratings2 = [self.user_item_matrix[user2][item] for item in common_items]
        
        if self.similarity == 'cosine':
            # 余弦相似度
            return 1 - cosine(ratings1, ratings2)
        elif self.similarity == 'pearson':
            # 皮尔逊相关系数
            if len(ratings1) < 2:
                return 0
            corr, _ = pearsonr(ratings1, ratings2)
            return corr if not np.isnan(corr) else 0
        elif self.similarity == 'euclidean':
            # 欧氏距离转换为相似度
            dist = np.sqrt(np.sum((np.array(ratings1) - np.array(ratings2))**2))
            return 1 / (1 + dist)
        else:
            raise ValueError(f"Unknown similarity: {self.similarity}")
    
    def predict(self, user_id, item_id):
        """
        预测用户对物品的评分
        
        Parameters:
        -----------
        user_id : int/str
            用户 ID
        item_id : int/str
            物品 ID
        
        Returns:
        --------
        float
            预测评分
        """
        if user_id not in self.user_item_matrix:
            return self.user_means.get(user_id, 3.0)  # 默认评分
        
        # 找到对 item_id 评过分的用户
        users_rated_item = []
        for user, items in self.user_item_matrix.items():
            if item_id in items:
                users_rated_item.append(user)
        
        if len(users_rated_item) == 0:
            return self.user_means.get(user_id, 3.0)
        
        # 计算与这些用户的相似度
        similarities = []
        ratings = []
        
        user_idx = self.user_to_idx[user_id]
        for other_user in users_rated_item:
            other_user_idx = self.user_to_idx[other_user]
            sim = self.similarity_matrix[user_idx][other_user_idx]
            if sim > 0:  # 只考虑正相似度
                similarities.append(sim)
                ratings.append(self.user_item_matrix[other_user][item_id])
        
        if len(similarities) == 0:
            return self.user_means.get(user_id, 3.0)
        
        # 选择 top-k 相似用户
        if len(similarities) > self.k:
            top_k_indices = np.argsort(similarities)[-self.k:]
            similarities = [similarities[i] for i in top_k_indices]
            ratings = [ratings[i] for i in top_k_indices]
        
        # 加权平均预测
        user_mean = self.user_means[user_id]
        numerator = sum(sim * (rating - self.user_means[other_user]) 
                       for sim, rating, other_user in zip(similarities, ratings, users_rated_item))
        denominator = sum(abs(sim) for sim in similarities)
        
        if denominator == 0:
            return user_mean
        
        return user_mean + numerator / denominator
    
    def recommend(self, user_id, n=10):
        """
        为用户推荐物品
        
        Parameters:
        -----------
        user_id : int/str
            用户 ID
        n : int
            推荐物品数量
        
        Returns:
        --------
        list
            [(item_id, predicted_rating), ...]
        """
        if user_id not in self.user_item_matrix:
            return []
        
        user_items = set(self.user_item_matrix[user_id].keys())
        all_items = set()
        for items in self.user_item_matrix.values():
            all_items.update(items.keys())
        
        candidate_items = all_items - user_items
        
        predictions = []
        for item_id in candidate_items:
            pred_rating = self.predict(user_id, item_id)
            predictions.append((item_id, pred_rating))
        
        # 按预测评分排序
        predictions.sort(key=lambda x: x[1], reverse=True)
        return predictions[:n]


# 使用示例
if __name__ == "__main__":
    # 构造示例数据
    user_item_matrix = {
        'Alice': {'肖申克': 5, '阿甘': 5, '泰坦尼克': 3, '教父': 4},
        'Bob': {'肖申克': 5, '阿甘': 5, '当幸福': 4, '泰坦尼克': 2},
        'Carol': {'肖申克': 4, '阿甘': 4, '当幸福': 3, '泰坦尼克': 5, '教父': 5},
        'David': {'肖申克': 2, '阿甘': 1, '泰坦尼克': 4, '教父': 3},
        'Eve': {'当幸福': 2, '泰坦尼克': 3, '教父': 4}
    }
    
    # 训练模型
    model = UserBasedCF(k=2, similarity='pearson')
    model.fit(user_item_matrix)
    
    # 预测 Alice 对《当幸福来敲门》的评分
    pred = model.predict('Alice', '当幸福')
    print(f"Alice 对《当幸福来敲门》的预测评分: {pred:.2f}")
    
    # 为 Alice 推荐电影
    recommendations = model.recommend('Alice', n=3)
    print("\n 为 Alice 推荐的电影:")
    for item, rating in recommendations:
        print(f"  {item}: {rating:.2f}")

User-CF 的优缺点

优点： - 直观易懂，符合人类推荐习惯 - 能发现用户潜在兴趣 - 推荐结果可解释性强

缺点： - 计算复杂度高：，其中 是用户数， 是物品数 - 用户数量增长时，相似度矩阵存储和计算成本急剧增加 - 数据稀疏时，找到共同评分的用户困难 - 新用户冷启动问题严重

基于物品的协同过滤（ Item-CF）

算法流程

Item-CF 的核心步骤：

  1. 计算物品相似度：找到与目标物品 最相似的 个物品
  2. 预测评分：基于用户 对这 个相似物品的评分，预测用户 对物品 的评分
  3. 生成推荐：选择预测评分最高的 个物品推荐给用户

为什么 Item-CF 更常用？

相比 User-CF， Item-CF 有以下优势：

  1. 物品数量通常少于用户数量：计算物品相似度矩阵的成本更低
  2. 物品相似度更稳定：物品的属性变化慢，相似度可以预先计算并缓存
  3. 推荐结果更稳定：用户兴趣变化时，物品相似度不会立即改变
  4. 可解释性更好："因为你喜欢 A，所以推荐相似的 B"

Amazon 在 2003 年的论文中证明了 Item-CF 的效果优于 User-CF，并成为工业界的主流方法。

物品相似度计算

设物品 和 被用户集合 （对两个物品都评过分的用户）评分。

1. 余弦相似度

2. 调整余弦相似度（常用）

注意：这里减去的是用户平均评分，而不是物品平均评分。这样做的目的是消除用户评分习惯的影响。

评分预测公式

其中 是与物品 最相似的 个物品集合。

如果考虑用户平均评分：

Item-CF 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
import numpy as np
from collections import defaultdict

class ItemBasedCF:
    def __init__(self, k=20, similarity='adjusted_cosine'):
        """
        Item-Based Collaborative Filtering
        
        Parameters:
        -----------
        k : int
            相似物品数量
        similarity : str
            相似度计算方法：'cosine', 'adjusted_cosine'
        """
        self.k = k
        self.similarity = similarity
        self.user_item_matrix = None
        self.item_user_matrix = None
        self.user_means = None
        self.similarity_matrix = None
        
    def fit(self, user_item_matrix):
        """
        训练模型
        
        Parameters:
        -----------
        user_item_matrix : dict
            {user_id: {item_id: rating }}
        """
        self.user_item_matrix = user_item_matrix
        
        # 构建物品-用户矩阵
        self.item_user_matrix = defaultdict(dict)
        for user_id, items in user_item_matrix.items():
            for item_id, rating in items.items():
                self.item_user_matrix[item_id][user_id] = rating
        
        # 计算用户平均评分
        self.user_means = {}
        for user_id, items in user_item_matrix.items():
            ratings = list(items.values())
            self.user_means[user_id] = np.mean(ratings) if ratings else 0
        
        # 计算物品相似度矩阵
        self._compute_similarity_matrix()
    
    def _compute_similarity_matrix(self):
        """计算物品相似度矩阵"""
        items = list(self.item_user_matrix.keys())
        n_items = len(items)
        self.similarity_matrix = {}
        self.item_to_idx = {item: idx for idx, item in enumerate(items)}
        
        for i, item1 in enumerate(items):
            for item2 in items[i+1:]:
                sim = self._compute_similarity(item1, item2)
                if sim > 0:  # 只存储正相似度
                    if item1 not in self.similarity_matrix:
                        self.similarity_matrix[item1] = {}
                    if item2 not in self.similarity_matrix:
                        self.similarity_matrix[item2] = {}
                    self.similarity_matrix[item1][item2] = sim
                    self.similarity_matrix[item2][item1] = sim
    
    def _compute_similarity(self, item1, item2):
        """计算两个物品的相似度"""
        users1 = set(self.item_user_matrix[item1].keys())
        users2 = set(self.item_user_matrix[item2].keys())
        common_users = users1 & users2
        
        if len(common_users) == 0:
            return 0
        
        if self.similarity == 'cosine':
            # 余弦相似度
            ratings1 = [self.item_user_matrix[item1][u] for u in common_users]
            ratings2 = [self.item_user_matrix[item2][u] for u in common_users]
            dot_product = sum(r1 * r2 for r1, r2 in zip(ratings1, ratings2))
            norm1 = np.sqrt(sum(r**2 for r in ratings1))
            norm2 = np.sqrt(sum(r**2 for r in ratings2))
            if norm1 == 0 or norm2 == 0:
                return 0
            return dot_product / (norm1 * norm2)
        
        elif self.similarity == 'adjusted_cosine':
            # 调整余弦相似度
            numerator = 0
            denom1 = 0
            denom2 = 0
            
            for user in common_users:
                r1 = self.item_user_matrix[item1][user]
                r2 = self.item_user_matrix[item2][user]
                user_mean = self.user_means[user]
                
                diff1 = r1 - user_mean
                diff2 = r2 - user_mean
                
                numerator += diff1 * diff2
                denom1 += diff1 ** 2
                denom2 += diff2 ** 2
            
            if denom1 == 0 or denom2 == 0:
                return 0
            
            return numerator / (np.sqrt(denom1) * np.sqrt(denom2))
        
        else:
            raise ValueError(f"Unknown similarity: {self.similarity}")
    
    def predict(self, user_id, item_id):
        """
        预测用户对物品的评分
        
        Parameters:
        -----------
        user_id : int/str
            用户 ID
        item_id : int/str
            物品 ID
        
        Returns:
        --------
        float
            预测评分
        """
        if user_id not in self.user_item_matrix:
            return self.user_means.get(user_id, 3.0)
        
        if item_id not in self.item_user_matrix:
            return self.user_means.get(user_id, 3.0)
        
        # 找到用户评过分的物品
        user_items = set(self.user_item_matrix[user_id].keys())
        
        # 找到与 item_id 相似的物品
        if item_id not in self.similarity_matrix:
            return self.user_means.get(user_id, 3.0)
        
        similar_items = self.similarity_matrix[item_id]
        
        # 找到用户评过分的相似物品
        rated_similar_items = {}
        for similar_item, sim in similar_items.items():
            if similar_item in user_items:
                rated_similar_items[similar_item] = sim
        
        if len(rated_similar_items) == 0:
            return self.user_means.get(user_id, 3.0)
        
        # 选择 top-k 相似物品
        sorted_items = sorted(rated_similar_items.items(), 
                            key=lambda x: x[1], reverse=True)[:self.k]
        
        # 加权平均预测
        user_mean = self.user_means[user_id]
        numerator = sum(sim * (self.user_item_matrix[user_id][item] - user_mean)
                       for item, sim in sorted_items)
        denominator = sum(abs(sim) for _, sim in sorted_items)
        
        if denominator == 0:
            return user_mean
        
        return user_mean + numerator / denominator
    
    def recommend(self, user_id, n=10):
        """
        为用户推荐物品
        
        Parameters:
        -----------
        user_id : int/str
            用户 ID
        n : int
            推荐物品数量
        
        Returns:
        --------
        list
            [(item_id, predicted_rating), ...]
        """
        if user_id not in self.user_item_matrix:
            return []
        
        user_items = set(self.user_item_matrix[user_id].keys())
        all_items = set(self.item_user_matrix.keys())
        candidate_items = all_items - user_items
        
        predictions = []
        for item_id in candidate_items:
            pred_rating = self.predict(user_id, item_id)
            predictions.append((item_id, pred_rating))
        
        predictions.sort(key=lambda x: x[1], reverse=True)
        return predictions[:n]


# 使用示例
if __name__ == "__main__":
    user_item_matrix = {
        'Alice': {'肖申克': 5, '阿甘': 5, '泰坦尼克': 3, '教父': 4},
        'Bob': {'肖申克': 5, '阿甘': 5, '当幸福': 4, '泰坦尼克': 2},
        'Carol': {'肖申克': 4, '阿甘': 4, '当幸福': 3, '泰坦尼克': 5, '教父': 5},
        'David': {'肖申克': 2, '阿甘': 1, '泰坦尼克': 4, '教父': 3},
        'Eve': {'当幸福': 2, '泰坦尼克': 3, '教父': 4}
    }
    
    model = ItemBasedCF(k=2, similarity='adjusted_cosine')
    model.fit(user_item_matrix)
    
    pred = model.predict('Alice', '当幸福')
    print(f"Alice 对《当幸福来敲门》的预测评分: {pred:.2f}")
    
    recommendations = model.recommend('Alice', n=3)
    print("\n 为 Alice 推荐的电影:")
    for item, rating in recommendations:
        print(f"  {item}: {rating:.2f}")

矩阵分解（ Matrix Factorization）

从协同过滤到矩阵分解

传统的协同过滤方法（ User-CF 和 Item-CF）存在明显的可扩展性问题：当用户和物品数量达到百万级别时，计算和存储相似度矩阵的成本变得不可接受。矩阵分解（ Matrix Factorization， MF）通过将高维稀疏矩阵分解为低维稠密矩阵的乘积，既解决了稀疏性问题，又大幅降低了计算复杂度。

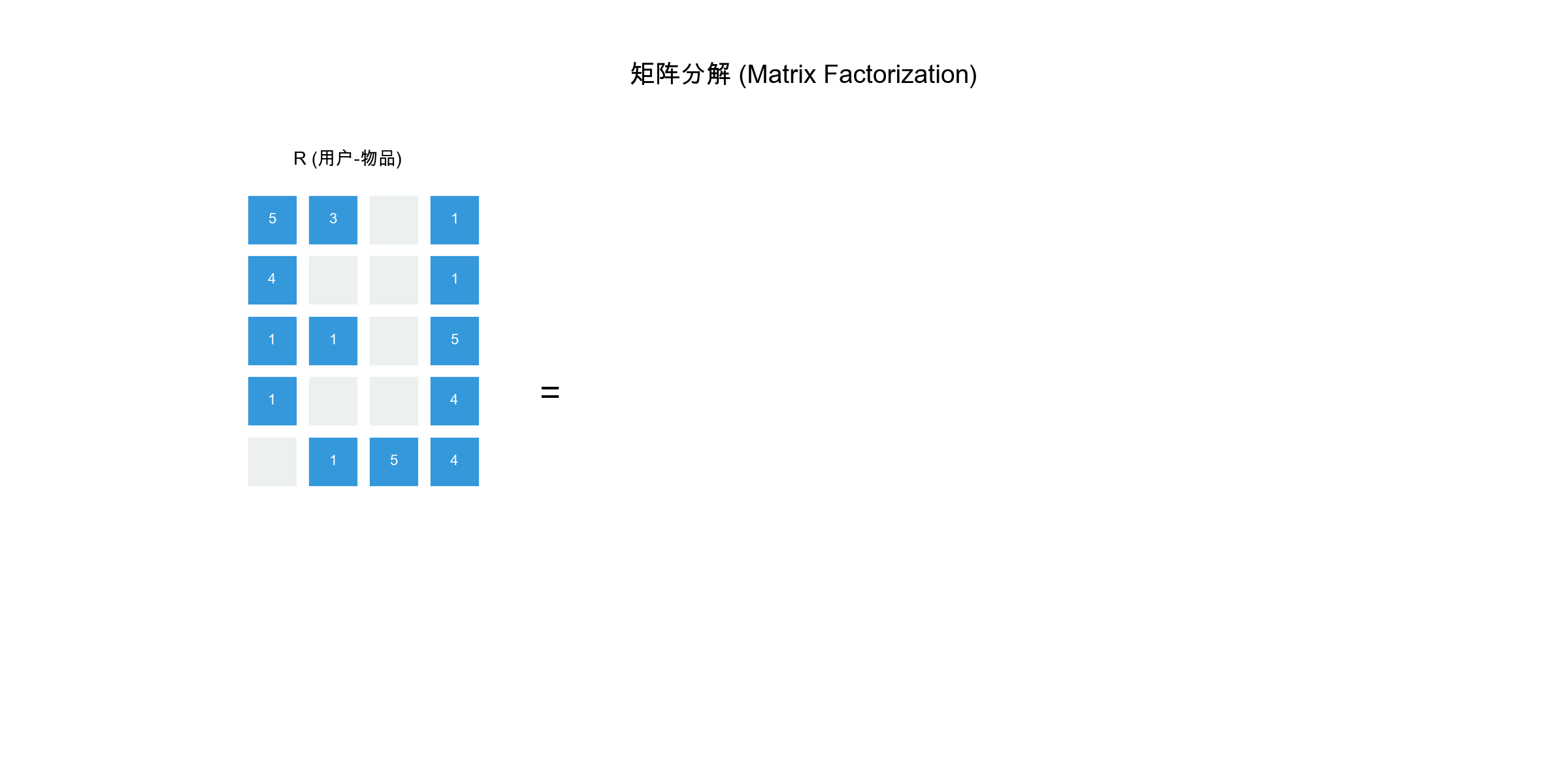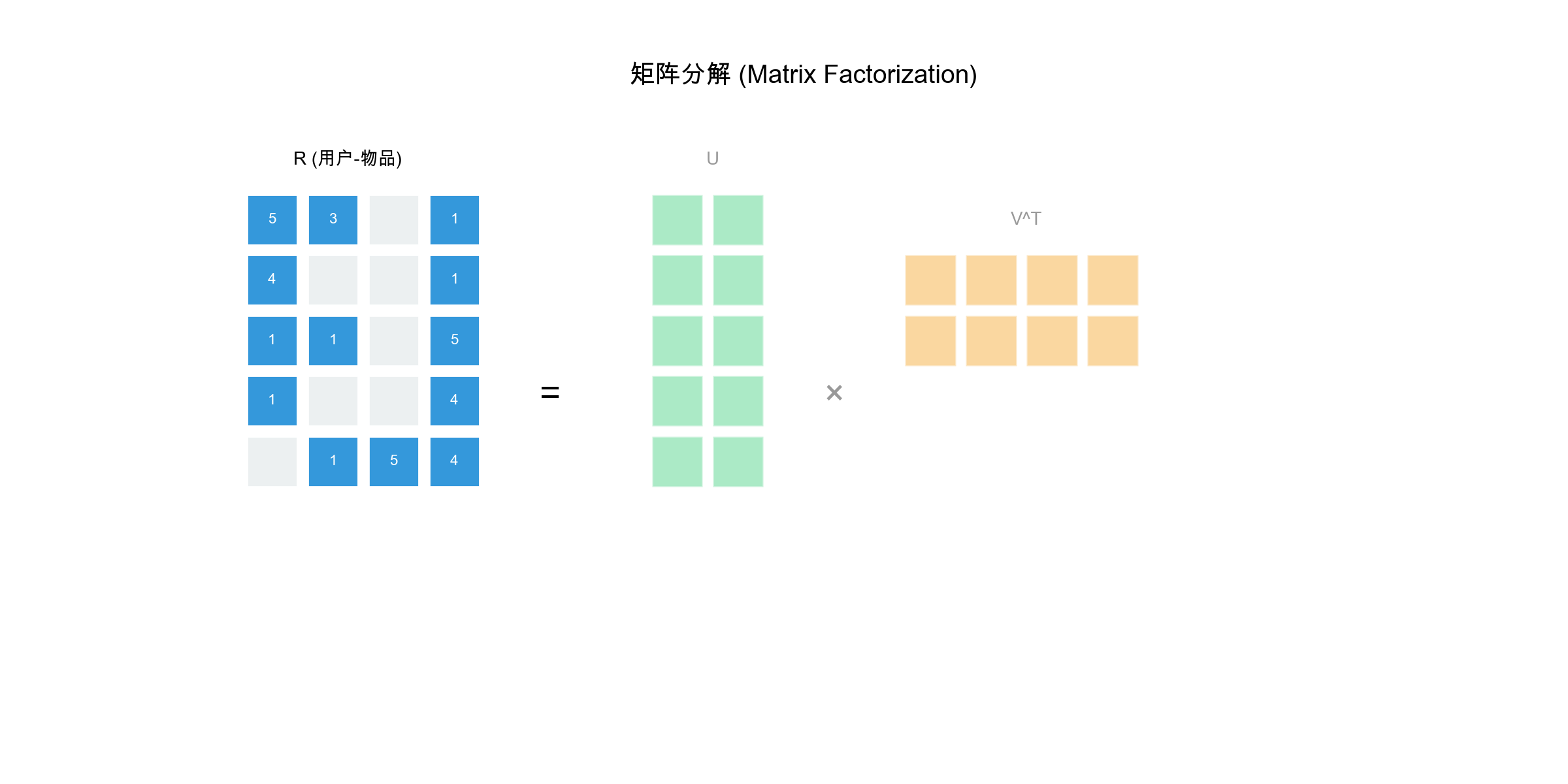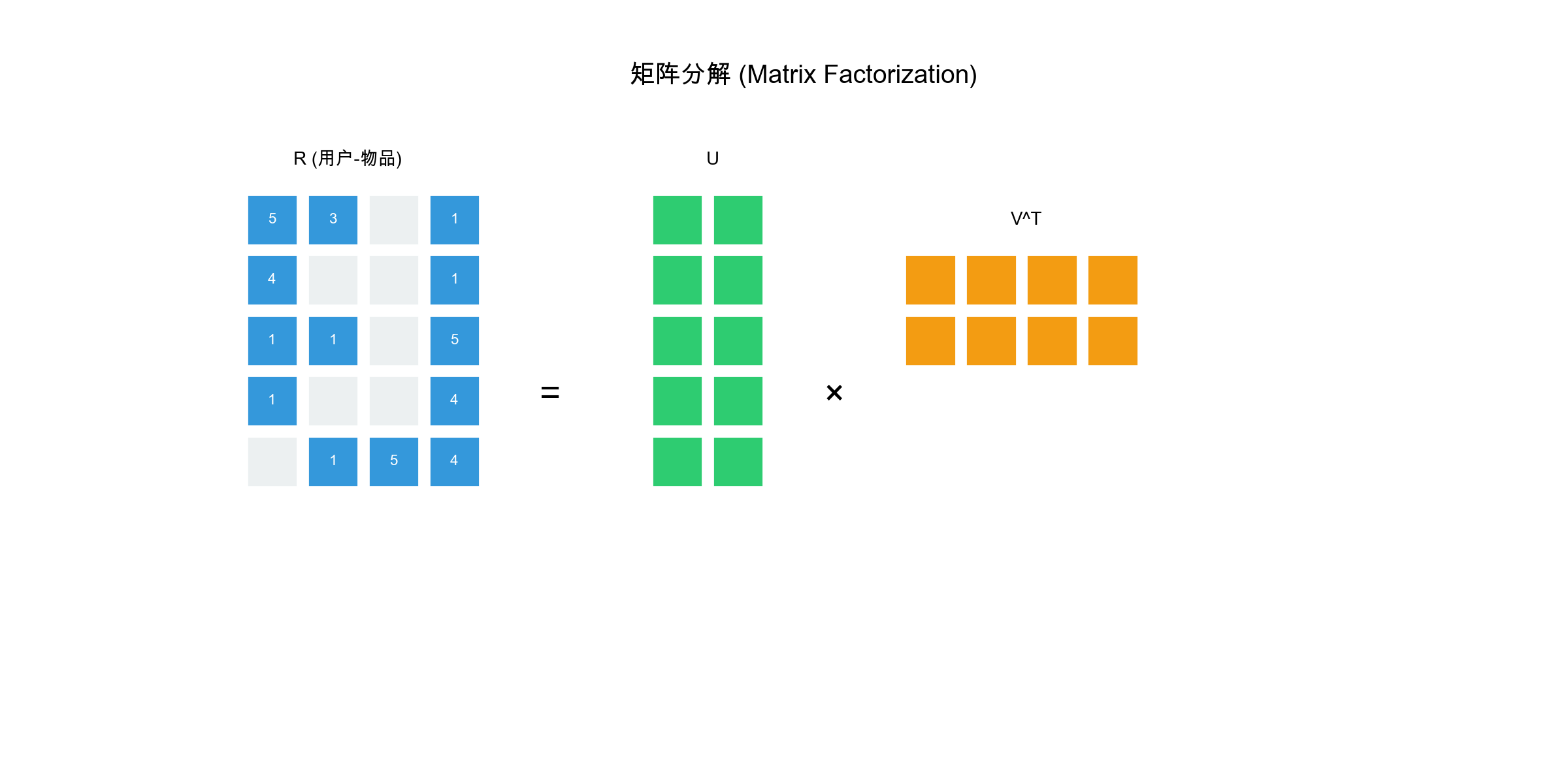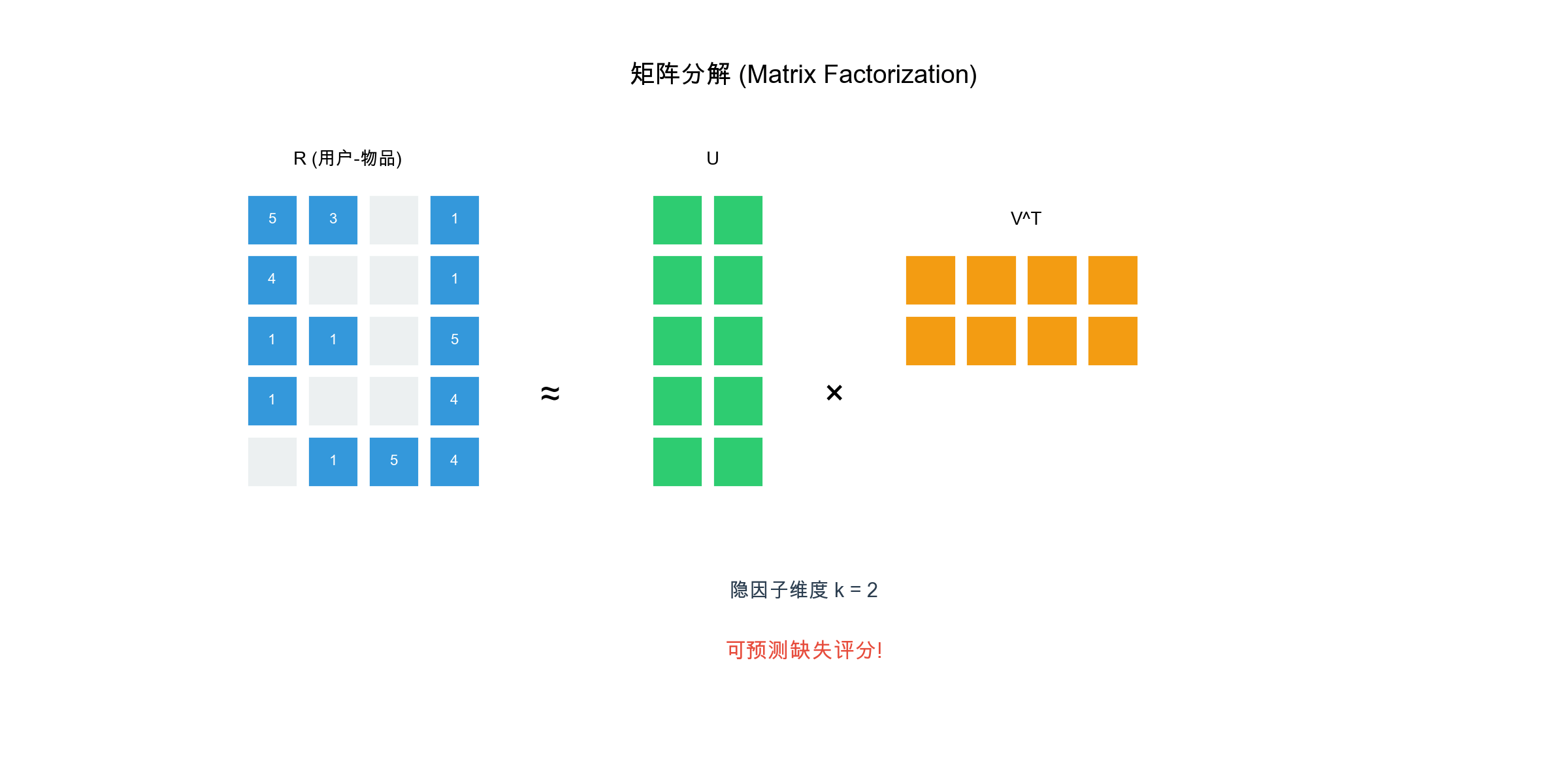
矩阵分解的基本思想

矩阵分解的核心是将用户-物品评分矩阵 （ 个用户， 个物品）分解为两个低维矩阵的乘积：

$$

R P Q^T$$

其中： - 是用户特征矩阵，每行 表示用户 的 维潜在特征向量 - 是物品特征矩阵，每行 表示物品 的 维潜在特征向量 - 是潜在特征维度（通常 ，如 50 、 100）

预测用户 对物品 的评分为：

矩阵分解的几何解释

矩阵分解可以理解为： - 用户向量 ：用户在 个潜在维度上的偏好强度 - 物品向量 ：物品在 个潜在维度上的特征强度 - 内积 ：用户偏好与物品特征的匹配程度

例如，如果 ，可能对应： - 维度 1：动作片 vs 文艺片 - 维度 2：喜剧 vs 悲剧 - 维度 3：现代 vs 古典

用户 Alice 的向量可能是 （喜欢动作片、不太喜欢喜剧、偏好现代），电影《肖申克的救赎》的向量可能是 （偏文艺、不太喜剧、现代），内积为 ，表示匹配度较高。

目标函数

矩阵分解的目标是找到 和 ，使得预测评分尽可能接近真实评分。定义损失函数：

其中： - 是已知评分的集合 - 第一项是平方误差损失（ MSE） - 第二项是正则化项，防止过拟合 - 是正则化系数

优化方法：随机梯度下降（ SGD）

对每个已知评分 ，计算预测误差：

$$

e_{ui} = r_{ui} - _{ui}$$

然后更新用户和物品向量：

其中 是学习率。

基础矩阵分解代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
import numpy as np
from collections import defaultdict
import random

class MatrixFactorization:
    def __init__(self, n_factors=50, learning_rate=0.01, reg=0.01, n_epochs=20):
        """
        基础矩阵分解模型
        
        Parameters:
        -----------
        n_factors : int
            潜在特征维度
        learning_rate : float
            学习率
        reg : float
            正则化系数
        n_epochs : int
            迭代次数
        """
        self.n_factors = n_factors
        self.learning_rate = learning_rate
        self.reg = reg
        self.n_epochs = n_epochs
        self.user_factors = None
        self.item_factors = None
        self.global_mean = None
        
    def fit(self, user_item_matrix):
        """训练模型"""
        users = list(user_item_matrix.keys())
        items = set()
        for items_dict in user_item_matrix.values():
            items.update(items_dict.keys())
        items = list(items)
        
        self.user_to_idx = {user: idx for idx, user in enumerate(users)}
        self.idx_to_user = {idx: user for idx, user in enumerate(users)}
        self.item_to_idx = {item: idx for idx, item in enumerate(items)}
        self.idx_to_item = {idx: item for idx, item in enumerate(items)}
        
        n_users = len(users)
        n_items = len(items)
        
        # 初始化用户和物品特征矩阵
        self.user_factors = np.random.normal(scale=0.1, size=(n_users, self.n_factors))
        self.item_factors = np.random.normal(scale=0.1, size=(n_items, self.n_factors))
        
        # 计算全局平均
        all_ratings = []
        for items_dict in user_item_matrix.values():
            all_ratings.extend(items_dict.values())
        self.global_mean = np.mean(all_ratings) if all_ratings else 0
        
        # 构建训练样本
        samples = []
        for user_id, items_dict in user_item_matrix.items():
            user_idx = self.user_to_idx[user_id]
            for item_id, rating in items_dict.items():
                item_idx = self.item_to_idx[item_id]
                samples.append((user_idx, item_idx, rating))
        
        # 训练
        for epoch in range(self.n_epochs):
            random.shuffle(samples)
            total_loss = 0
            
            for user_idx, item_idx, rating in samples:
                # 预测评分
                pred = np.dot(self.user_factors[user_idx], self.item_factors[item_idx])
                error = rating - pred
                
                # 更新参数
                user_factor = self.user_factors[user_idx].copy()
                item_factor = self.item_factors[item_idx].copy()
                
                self.user_factors[user_idx] += self.learning_rate * (
                    error * item_factor - self.reg * self.user_factors[user_idx]
                )
                self.item_factors[item_idx] += self.learning_rate * (
                    error * user_factor - self.reg * self.item_factors[item_idx]
                )
                
                total_loss += error ** 2
            
            if (epoch + 1) % 5 == 0:
                rmse = np.sqrt(total_loss / len(samples))
                print(f"Epoch {epoch + 1}, RMSE: {rmse:.4f}")
    
    def predict(self, user_id, item_id):
        """预测评分"""
        if user_id not in self.user_to_idx or item_id not in self.item_to_idx:
            return self.global_mean
        
        user_idx = self.user_to_idx[user_id]
        item_idx = self.item_to_idx[item_id]
        pred = np.dot(self.user_factors[user_idx], self.item_factors[item_idx])
        return pred
    
    def recommend(self, user_id, n=10):
        """推荐物品"""
        if user_id not in self.user_to_idx:
            return []
        
        predictions = []
        for item_idx in range(len(self.item_factors)):
            item_id = self.idx_to_item[item_idx]
            pred = self.predict(user_id, item_id)
            predictions.append((item_id, pred))
        
        predictions.sort(key=lambda x: x[1], reverse=True)
        return predictions[:n]

带偏置的矩阵分解（ Biased MF）

为什么需要偏置项？

基础矩阵分解假设评分只由用户和物品的潜在特征决定，但实际上： - 用户偏置：有些用户习惯打高分，有些习惯打低分 - 物品偏置：热门物品平均分高，冷门物品平均分低 - 全局偏置：整体评分水平（如平均 3.5 分）

引入偏置项后，预测公式变为：

其中： - 是全局平均评分 - 是用户 的偏置（相对于全局平均） - 是物品 的偏置（相对于全局平均）

偏置项的计算

初始化： $$

b_u = {i I_u} (r{ui} - )

b_i = {u U_i} (r{ui} - - b_u)$$

其中 是用户 评过分的物品集合， 是对物品 评过分的用户集合。

带偏置的矩阵分解代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
class BiasedMatrixFactorization:
    def __init__(self, n_factors=50, learning_rate=0.01, reg=0.01, reg_bias=0.01, n_epochs=20):
        """带偏置的矩阵分解模型"""
        self.n_factors = n_factors
        self.learning_rate = learning_rate
        self.reg = reg
        self.reg_bias = reg_bias
        self.n_epochs = n_epochs
        self.user_factors = None
        self.item_factors = None
        self.user_bias = None
        self.item_bias = None
        self.global_mean = None
        
    def fit(self, user_item_matrix):
        """训练模型"""
        users = list(user_item_matrix.keys())
        items = set()
        for items_dict in user_item_matrix.values():
            items.update(items_dict.keys())
        items = list(items)
        
        self.user_to_idx = {user: idx for idx, user in enumerate(users)}
        self.idx_to_user = {idx: user for idx, user in enumerate(users)}
        self.item_to_idx = {item: idx for idx, item in enumerate(items)}
        self.idx_to_item = {idx: item for idx, item in enumerate(items)}
        
        n_users = len(users)
        n_items = len(items)
        
        # 初始化
        self.user_factors = np.random.normal(scale=0.1, size=(n_users, self.n_factors))
        self.item_factors = np.random.normal(scale=0.1, size=(n_items, self.n_factors))
        self.user_bias = np.zeros(n_users)
        self.item_bias = np.zeros(n_items)
        
        # 计算全局平均
        all_ratings = []
        for items_dict in user_item_matrix.values():
            all_ratings.extend(items_dict.values())
        self.global_mean = np.mean(all_ratings) if all_ratings else 0
        
        # 初始化偏置项
        for user_id, items_dict in user_item_matrix.items():
            user_idx = self.user_to_idx[user_id]
            ratings = list(items_dict.values())
            self.user_bias[user_idx] = np.mean(ratings) - self.global_mean
        
        for item_idx in range(n_items):
            item_id = self.idx_to_item[item_idx]
            ratings = []
            for user_id, items_dict in user_item_matrix.items():
                if item_id in items_dict:
                    ratings.append(items_dict[item_id])
            if ratings:
                self.item_bias[item_idx] = np.mean(ratings) - self.global_mean
        
        # 构建训练样本
        samples = []
        for user_id, items_dict in user_item_matrix.items():
            user_idx = self.user_to_idx[user_id]
            for item_id, rating in items_dict.items():
                item_idx = self.item_to_idx[item_id]
                samples.append((user_idx, item_idx, rating))
        
        # 训练
        for epoch in range(self.n_epochs):
            random.shuffle(samples)
            total_loss = 0
            
            for user_idx, item_idx, rating in samples:
                # 预测评分
                pred = (self.global_mean + 
                       self.user_bias[user_idx] + 
                       self.item_bias[item_idx] +
                       np.dot(self.user_factors[user_idx], self.item_factors[item_idx]))
                error = rating - pred
                
                # 更新参数
                user_factor = self.user_factors[user_idx].copy()
                item_factor = self.item_factors[item_idx].copy()
                
                self.user_factors[user_idx] += self.learning_rate * (
                    error * item_factor - self.reg * self.user_factors[user_idx]
                )
                self.item_factors[item_idx] += self.learning_rate * (
                    error * user_factor - self.reg * self.item_factors[item_idx]
                )
                self.user_bias[user_idx] += self.learning_rate * (
                    error - self.reg_bias * self.user_bias[user_idx]
                )
                self.item_bias[item_idx] += self.learning_rate * (
                    error - self.reg_bias * self.item_bias[item_idx]
                )
                
                total_loss += error ** 2
            
            if (epoch + 1) % 5 == 0:
                rmse = np.sqrt(total_loss / len(samples))
                print(f"Epoch {epoch + 1}, RMSE: {rmse:.4f}")
    
    def predict(self, user_id, item_id):
        """预测评分"""
        if user_id not in self.user_to_idx or item_id not in self.item_to_idx:
            return self.global_mean
        
        user_idx = self.user_to_idx[user_id]
        item_idx = self.item_to_idx[item_id]
        
        pred = (self.global_mean + 
               self.user_bias[user_idx] + 
               self.item_bias[item_idx] +
               np.dot(self.user_factors[user_idx], self.item_factors[item_idx]))
        return pred
    
    def recommend(self, user_id, n=10):
        """推荐物品"""
        if user_id not in self.user_to_idx:
            return []
        
        predictions = []
        for item_idx in range(len(self.item_factors)):
            item_id = self.idx_to_item[item_idx]
            pred = self.predict(self.idx_to_user[user_idx], item_id)
            predictions.append((item_id, pred))
        
        predictions.sort(key=lambda x: x[1], reverse=True)
        return predictions[:n]

SVD 与 SVD++

奇异值分解（ SVD）

传统的 SVD 要求矩阵是完整的，但评分矩阵是稀疏的。 Netflix Prize 竞赛中，研究者提出了适用于稀疏矩阵的 SVD 方法，实际上就是带偏置的矩阵分解。

SVD++：考虑隐式反馈

SVD++ 在 SVD 的基础上引入了隐式反馈（ implicit feedback）。隐式反馈是指用户没有明确评分但可能表达偏好的行为，如： - 浏览但未购买 - 点击但未评分 - 观看时长 - 收藏、分享

SVD++ 的预测公式：

其中： - 是用户 的显式反馈特征向量 - 是用户 有隐式反馈的物品集合 - 是物品 的隐式反馈特征向量 - 是归一化因子

SVD++ 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
class SVDPlusPlus:
    def __init__(self, n_factors=50, learning_rate=0.01, reg=0.01, reg_bias=0.01, n_epochs=20):
        """SVD++ 模型"""
        self.n_factors = n_factors
        self.learning_rate = learning_rate
        self.reg = reg
        self.reg_bias = reg_bias
        self.n_epochs = n_epochs
        self.user_factors = None
        self.item_factors = None
        self.item_implicit_factors = None
        self.user_bias = None
        self.item_bias = None
        self.global_mean = None
        
    def fit(self, user_item_matrix, implicit_feedback=None):
        """训练模型"""
        users = list(user_item_matrix.keys())
        items = set()
        for items_dict in user_item_matrix.values():
            items.update(items_dict.keys())
        if implicit_feedback:
            for item_list in implicit_feedback.values():
                items.update(item_list)
        items = list(items)
        
        self.user_to_idx = {user: idx for idx, user in enumerate(users)}
        self.idx_to_user = {idx: user for idx, user in enumerate(users)}
        self.item_to_idx = {item: idx for idx, item in enumerate(items)}
        self.idx_to_item = {idx: item for idx, item in enumerate(items)}
        
        n_users = len(users)
        n_items = len(items)
        
        # 初始化
        self.user_factors = np.random.normal(scale=0.1, size=(n_users, self.n_factors))
        self.item_factors = np.random.normal(scale=0.1, size=(n_items, self.n_factors))
        self.item_implicit_factors = np.random.normal(scale=0.1, size=(n_items, self.n_factors))
        self.user_bias = np.zeros(n_users)
        self.item_bias = np.zeros(n_items)
        
        # 计算全局平均
        all_ratings = []
        for items_dict in user_item_matrix.values():
            all_ratings.extend(items_dict.values())
        self.global_mean = np.mean(all_ratings) if all_ratings else 0
        
        # 初始化偏置
        for user_id, items_dict in user_item_matrix.items():
            user_idx = self.user_to_idx[user_id]
            ratings = list(items_dict.values())
            self.user_bias[user_idx] = np.mean(ratings) - self.global_mean
        
        for item_idx in range(n_items):
            item_id = self.idx_to_item[item_idx]
            ratings = []
            for user_id, items_dict in user_item_matrix.items():
                if item_id in items_dict:
                    ratings.append(items_dict[item_id])
            if ratings:
                self.item_bias[item_idx] = np.mean(ratings) - self.global_mean
        
        # 构建隐式反馈集合
        if implicit_feedback is None:
            implicit_feedback = {}
            for user_id, items_dict in user_item_matrix.items():
                implicit_feedback[user_id] = list(items_dict.keys())
        
        self.user_implicit_items = {}
        for user_id in users:
            if user_id in implicit_feedback:
                self.user_implicit_items[user_id] = [
                    self.item_to_idx[item] for item in implicit_feedback[user_id]
                    if item in self.item_to_idx
                ]
            else:
                self.user_implicit_items[user_id] = []
        
        # 构建训练样本
        samples = []
        for user_id, items_dict in user_item_matrix.items():
            user_idx = self.user_to_idx[user_id]
            for item_id, rating in items_dict.items():
                item_idx = self.item_to_idx[item_id]
                samples.append((user_idx, item_idx, rating))
        
        # 训练
        for epoch in range(self.n_epochs):
            random.shuffle(samples)
            total_loss = 0
            
            for user_idx, item_idx, rating in samples:
                # 计算用户增强特征向量
                user_id = self.idx_to_user[user_idx]
                implicit_items = self.user_implicit_items[user_id]
                
                if len(implicit_items) > 0:
                    implicit_sum = np.sum(
                        [self.item_implicit_factors[j] for j in implicit_items], axis=0
                    )
                    norm_factor = 1.0 / np.sqrt(len(implicit_items))
                    enhanced_user_factor = self.user_factors[user_idx] + norm_factor * implicit_sum
                else:
                    enhanced_user_factor = self.user_factors[user_idx]
                
                # 预测评分
                pred = (self.global_mean + 
                       self.user_bias[user_idx] + 
                       self.item_bias[item_idx] +
                       np.dot(enhanced_user_factor, self.item_factors[item_idx]))
                error = rating - pred
                
                # 更新参数
                user_factor = self.user_factors[user_idx].copy()
                item_factor = self.item_factors[item_idx].copy()
                
                # 更新显式特征
                self.user_factors[user_idx] += self.learning_rate * (
                    error * item_factor - self.reg * self.user_factors[user_idx]
                )
                self.item_factors[item_idx] += self.learning_rate * (
                    error * enhanced_user_factor - self.reg * self.item_factors[item_idx]
                )
                
                # 更新隐式特征
                if len(implicit_items) > 0:
                    norm_factor = 1.0 / np.sqrt(len(implicit_items))
                    for j in implicit_items:
                        self.item_implicit_factors[j] += self.learning_rate * (
                            error * norm_factor * item_factor - 
                            self.reg * self.item_implicit_factors[j]
                        )
                
                # 更新偏置
                self.user_bias[user_idx] += self.learning_rate * (
                    error - self.reg_bias * self.user_bias[user_idx]
                )
                self.item_bias[item_idx] += self.learning_rate * (
                    error - self.reg_bias * self.item_bias[item_idx]
                )
                
                total_loss += error ** 2
            
            if (epoch + 1) % 5 == 0:
                rmse = np.sqrt(total_loss / len(samples))
                print(f"Epoch {epoch + 1}, RMSE: {rmse:.4f}")
    
    def predict(self, user_id, item_id):
        """预测评分"""
        if user_id not in self.user_to_idx or item_id not in self.item_to_idx:
            return self.global_mean
        
        user_idx = self.user_to_idx[user_id]
        item_idx = self.item_to_idx[item_id]
        
        # 计算用户增强特征向量
        implicit_items = self.user_implicit_items.get(user_id, [])
        if len(implicit_items) > 0:
            implicit_sum = np.sum(
                [self.item_implicit_factors[j] for j in implicit_items], axis=0
            )
            norm_factor = 1.0 / np.sqrt(len(implicit_items))
            enhanced_user_factor = self.user_factors[user_idx] + norm_factor * implicit_sum
        else:
            enhanced_user_factor = self.user_factors[user_idx]
        
        pred = (self.global_mean + 
               self.user_bias[user_idx] + 
               self.item_bias[item_idx] +
               np.dot(enhanced_user_factor, self.item_factors[item_idx]))
        return pred
    
    def recommend(self, user_id, n=10):
        """推荐物品"""
        if user_id not in self.user_to_idx:
            return []
        
        predictions = []
        for item_idx in range(len(self.item_factors)):
            item_id = self.idx_to_item[item_idx]
            pred = self.predict(user_id, item_id)
            predictions.append((item_id, pred))
        
        predictions.sort(key=lambda x: x[1], reverse=True)
        return predictions[:n]

ALS：交替最小二乘法

为什么需要 ALS？

随机梯度下降（ SGD）虽然简单，但在大规模数据上训练速度较慢。交替最小二乘法（ Alternating Least Squares， ALS）通过固定一个变量优化另一个变量，可以并行化计算，大幅提升训练速度。

ALS 算法原理

ALS 的核心思想是交替优化用户向量和物品向量：

  1. 固定物品向量 ，优化用户向量 ：
    • 对每个用户 $ u，求解最小二乘问题：$
  • 解析解：

其中 是用户 评过分的物品的特征矩阵， 是对应的评分向量。

  1. 固定用户向量 ，优化物品向量 ：
    • 对每个物品 $ i，求解最小二乘问题：$
  • 解析解：

其中 是对物品 评过分的用户的特征矩阵， 是对应的评分向量。

  1. 交替迭代：重复步骤 1 和 2，直到收敛。

ALS 的优势

  • 可并行化：不同用户/物品的优化可以并行计算
  • 收敛速度快：每次迭代都有解析解
  • 适合大规模数据： Spark MLlib 等框架都实现了 ALS

ALS 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
class ALSMatrixFactorization:
    def __init__(self, n_factors=50, reg=0.01, n_epochs=20):
        """ALS 矩阵分解模型"""
        self.n_factors = n_factors
        self.reg = reg
        self.n_epochs = n_epochs
        self.user_factors = None
        self.item_factors = None
        
    def fit(self, user_item_matrix):
        """训练模型"""
        users = list(user_item_matrix.keys())
        items = set()
        for items_dict in user_item_matrix.values():
            items.update(items_dict.keys())
        items = list(items)
        
        self.user_to_idx = {user: idx for idx, user in enumerate(users)}
        self.idx_to_user = {idx: user for idx, user in enumerate(users)}
        self.item_to_idx = {item: idx for idx, item in enumerate(items)}
        self.idx_to_item = {idx: item for idx, item in enumerate(items)}
        
        n_users = len(users)
        n_items = len(items)
        
        # 初始化
        self.user_factors = np.random.normal(scale=0.1, size=(n_users, self.n_factors))
        self.item_factors = np.random.normal(scale=0.1, size=(n_items, self.n_factors))
        
        # 构建用户-物品评分矩阵（稀疏）
        self.user_items = {}
        self.item_users = {}
        for user_id, items_dict in user_item_matrix.items():
            user_idx = self.user_to_idx[user_id]
            self.user_items[user_idx] = {}
            for item_id, rating in items_dict.items():
                item_idx = self.item_to_idx[item_id]
                self.user_items[user_idx][item_idx] = rating
                if item_idx not in self.item_users:
                    self.item_users[item_idx] = {}
                self.item_users[item_idx][user_idx] = rating
        
        # ALS 迭代
        lambda_eye = self.reg * np.eye(self.n_factors)
        
        for epoch in range(self.n_epochs):
            # 固定物品向量，优化用户向量
            for user_idx in range(n_users):
                if user_idx not in self.user_items:
                    continue
                
                items_rated = list(self.user_items[user_idx].keys())
                ratings = [self.user_items[user_idx][i] for i in items_rated]
                
                if len(items_rated) == 0:
                    continue
                
                Q_u = self.item_factors[items_rated]
                r_u = np.array(ratings)
                
                # 求解 (Q_u^T Q_u + lambda I) p_u = Q_u^T r_u
                A = Q_u.T.dot(Q_u) + lambda_eye
                b = Q_u.T.dot(r_u)
                self.user_factors[user_idx] = np.linalg.solve(A, b)
            
            # 固定用户向量，优化物品向量
            for item_idx in range(n_items):
                if item_idx not in self.item_users:
                    continue
                
                users_rated = list(self.item_users[item_idx].keys())
                ratings = [self.item_users[item_idx][u] for u in users_rated]
                
                if len(users_rated) == 0:
                    continue
                
                P_i = self.user_factors[users_rated]
                r_i = np.array(ratings)
                
                # 求解 (P_i^T P_i + lambda I) q_i = P_i^T r_i
                A = P_i.T.dot(P_i) + lambda_eye
                b = P_i.T.dot(r_i)
                self.item_factors[item_idx] = np.linalg.solve(A, b)
            
            # 计算 RMSE
            if (epoch + 1) % 5 == 0:
                total_error = 0
                count = 0
                for user_idx, items_dict in self.user_items.items():
                    for item_idx, rating in items_dict.items():
                        pred = np.dot(self.user_factors[user_idx], self.item_factors[item_idx])
                        total_error += (rating - pred) ** 2
                        count += 1
                rmse = np.sqrt(total_error / count) if count > 0 else 0
                print(f"Epoch {epoch + 1}, RMSE: {rmse:.4f}")
    
    def predict(self, user_id, item_id):
        """预测评分"""
        if user_id not in self.user_to_idx or item_id not in self.item_to_idx:
            return 0
        
        user_idx = self.user_to_idx[user_id]
        item_idx = self.item_to_idx[item_id]
        pred = np.dot(self.user_factors[user_idx], self.item_factors[item_idx])
        return pred
    
    def recommend(self, user_id, n=10):
        """推荐物品"""
        if user_id not in self.user_to_idx:
            return []
        
        predictions = []
        for item_idx in range(len(self.item_factors)):
            item_id = self.idx_to_item[item_idx]
            pred = self.predict(user_id, item_id)
            predictions.append((item_id, pred))
        
        predictions.sort(key=lambda x: x[1], reverse=True)
        return predictions[:n]

BPR：贝叶斯个性化排序

从评分预测到排序学习

传统的矩阵分解方法（ MF 、 SVD++）都是评分预测任务：预测用户对物品的评分。但在实际推荐场景中，我们更关心的是排序：将用户最可能喜欢的物品排在前面。

BPR（ Bayesian Personalized Ranking）将推荐问题转化为排序学习问题，直接优化排序指标（如 AUC 、 NDCG），而不是评分预测的 RMSE 。

BPR 的核心思想

BPR 假设：用户更喜欢他评过分的物品，而不是未评分的物品。

对于用户 ，如果他对物品 有正反馈（如评分、点击），对物品 没有反馈，则认为 更喜欢 而不是 ，即：

$$

r_{ui} > r_{uj}$$

BPR 的目标函数

BPR 使用贝叶斯方法最大化后验概率：

$$

p(| >_u) p(>_u | ) p()$$

其中： - 表示用户 的偏好排序 - 是模型参数（用户和物品向量）

定义：

$$

p(>u | ) = {(u,i,j) D_S} p(i >_u j | )$$

其中 是训练样本集合，每个样本是三元组 ，表示用户 更喜欢物品 而不是 。

定义：

$$

p(i >u j | ) = ({uij})$$

其中 ， 是 sigmoid 函数。

最终的目标函数（对数似然）：

BPR 优化

使用随机梯度下降更新参数：

对每个样本 ：

对于矩阵分解模型 ：

BPR 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
class BPRMatrixFactorization:
    def __init__(self, n_factors=50, learning_rate=0.01, reg=0.01, n_epochs=20):
        """BPR 矩阵分解模型"""
        self.n_factors = n_factors
        self.learning_rate = learning_rate
        self.reg = reg
        self.n_epochs = n_epochs
        self.user_factors = None
        self.item_factors = None
        
    def fit(self, user_item_matrix):
        """训练模型"""
        users = list(user_item_matrix.keys())
        items = set()
        for items_dict in user_item_matrix.values():
            items.update(items_dict.keys())
        items = list(items)
        
        self.user_to_idx = {user: idx for idx, user in enumerate(users)}
        self.idx_to_user = {idx: user for idx, user in enumerate(users)}
        self.item_to_idx = {item: idx for idx, item in enumerate(items)}
        self.idx_to_item = {idx: item for idx, item in enumerate(items)}
        
        n_users = len(users)
        n_items = len(items)
        
        # 初始化
        self.user_factors = np.random.normal(scale=0.1, size=(n_users, self.n_factors))
        self.item_factors = np.random.normal(scale=0.1, size=(n_items, self.n_factors))
        
        # 构建训练样本：对每个用户，正样本物品 vs 负样本物品
        self.user_items = {}
        for user_id, items_dict in user_item_matrix.items():
            user_idx = self.user_to_idx[user_id]
            self.user_items[user_idx] = set(items_dict.keys())
        
        all_items = set(items)
        
        # 训练
        for epoch in range(self.n_epochs):
            total_loss = 0
            sample_count = 0
            
            for user_idx in range(n_users):
                if user_idx not in self.user_items:
                    continue
                
                positive_items = self.user_items[user_idx]
                negative_items = all_items - positive_items
                
                if len(positive_items) == 0 or len(negative_items) == 0:
                    continue
                
                # 对每个正样本，采样一个负样本
                for pos_item_id in positive_items:
                    pos_item_idx = self.item_to_idx[pos_item_id]
                    
                    # 随机采样负样本
                    neg_item_id = random.choice(list(negative_items))
                    neg_item_idx = self.item_to_idx[neg_item_id]
                    
                    # 计算预测
                    r_ui = np.dot(self.user_factors[user_idx], self.item_factors[pos_item_idx])
                    r_uj = np.dot(self.user_factors[user_idx], self.item_factors[neg_item_idx])
                    r_uij = r_ui - r_uj
                    
                    # 计算梯度
                    x_uij = 1 / (1 + np.exp(r_uij))  # sigmoid 的导数
                    
                    # 更新参数
                    user_factor = self.user_factors[user_idx].copy()
                    
                    self.user_factors[user_idx] += self.learning_rate * (
                        x_uij * (self.item_factors[pos_item_idx] - self.item_factors[neg_item_idx]) -
                        self.reg * self.user_factors[user_idx]
                    )
                    self.item_factors[pos_item_idx] += self.learning_rate * (
                        x_uij * user_factor - self.reg * self.item_factors[pos_item_idx]
                    )
                    self.item_factors[neg_item_idx] += self.learning_rate * (
                        -x_uij * user_factor - self.reg * self.item_factors[neg_item_idx]
                    )
                    
                    total_loss += np.log(1 / (1 + np.exp(-r_uij)))
                    sample_count += 1
            
            if (epoch + 1) % 5 == 0:
                avg_loss = total_loss / sample_count if sample_count > 0 else 0
                print(f"Epoch {epoch + 1}, Average Loss: {avg_loss:.4f}")
    
    def predict(self, user_id, item_id):
        """预测用户对物品的偏好分数"""
        if user_id not in self.user_to_idx or item_id not in self.item_to_idx:
            return 0
        
        user_idx = self.user_to_idx[user_id]
        item_idx = self.item_to_idx[item_id]
        pred = np.dot(self.user_factors[user_idx], self.item_factors[item_idx])
        return pred
    
    def recommend(self, user_id, n=10):
        """推荐物品"""
        if user_id not in self.user_to_idx:
            return []
        
        predictions = []
        for item_idx in range(len(self.item_factors)):
            item_id = self.idx_to_item[item_idx]
            pred = self.predict(user_id, item_id)
            predictions.append((item_id, pred))
        
        predictions.sort(key=lambda x: x[1], reverse=True)
        return predictions[:n]

因子分解机（ Factorization Machines）

FM 的动机

因子分解机（ Factorization Machines， FM）由 Steffen Rendle 在 2010 年提出，最初用于解决稀疏特征的回归和分类问题。在推荐系统中， FM 可以同时利用： - 用户特征：年龄、性别、地域等 - 物品特征：类别、价格、品牌等 - 用户-物品交互：历史评分、点击等

FM 模型

FM 的预测公式：

其中： - 是全局偏置 - 是特征 的权重 - 是特征 的 维潜在向量 - 是向量内积

FM 的优势

  1. 处理稀疏特征：通过向量内积捕捉特征交互，即使特征对在训练集中很少出现
  2. 线性时间复杂度：可以重写为线性复杂度： 3. 通用性强：可以用于回归、分类、排序等多种任务

FM 在推荐系统中的应用

在推荐系统中，特征向量 通常包括： - 用户 one-hot 编码：如 表示用户 3 - 物品 one-hot 编码：如 表示物品 2 - 其他特征：用户年龄、物品类别等

FM 可以自动学习： - 用户-物品交互： - 用户-特征交互： - 物品-特征交互：

FM 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
class FactorizationMachine:
    def __init__(self, n_factors=10, learning_rate=0.01, reg=0.01, n_epochs=20):
        """因子分解机"""
        self.n_factors = n_factors
        self.learning_rate = learning_rate
        self.reg = reg
        self.n_epochs = n_epochs
        self.w0 = 0
        self.w = None
        self.v = None
        
    def fit(self, X, y):
        """
        训练模型
        
        Parameters:
        -----------
        X : np.ndarray
            特征矩阵， shape=(n_samples, n_features)
        y : np.ndarray
            标签， shape=(n_samples,)
        """
        n_samples, n_features = X.shape
        
        # 初始化参数
        self.w0 = np.mean(y)
        self.w = np.zeros(n_features)
        self.v = np.random.normal(scale=0.1, size=(n_features, self.n_factors))
        
        # 训练
        for epoch in range(self.n_epochs):
            total_loss = 0
            
            for idx in range(n_samples):
                x = X[idx]
                y_true = y[idx]
                
                # 预测
                y_pred = self._predict_single(x)
                error = y_true - y_pred
                
                # 更新 w0
                self.w0 += self.learning_rate * error
                
                # 更新 w
                for i in range(n_features):
                    if x[i] != 0:
                        self.w[i] += self.learning_rate * (error * x[i] - self.reg * self.w[i])
                
                # 更新 v
                for i in range(n_features):
                    if x[i] != 0:
                        # 计算交互项对 v[i] 的梯度
                        sum_vx = np.sum([self.v[j] * x[j] for j in range(n_features) if j != i], axis=0)
                        grad_v = error * x[i] * sum_vx - self.reg * self.v[i]
                        self.v[i] += self.learning_rate * grad_v
                
                total_loss += error ** 2
            
            if (epoch + 1) % 5 == 0:
                rmse = np.sqrt(total_loss / n_samples)
                print(f"Epoch {epoch + 1}, RMSE: {rmse:.4f}")
    
    def _predict_single(self, x):
        """预测单个样本"""
        # 线性项
        linear = np.dot(self.w, x)
        
        # 交互项（使用优化后的公式）
        interaction = 0
        sum_vx = np.zeros(self.n_factors)
        sum_vx_sq = 0
        
        for i in range(len(x)):
            if x[i] != 0:
                vx = self.v[i] * x[i]
                sum_vx += vx
                sum_vx_sq += np.dot(vx, vx)
        
        interaction = 0.5 * (np.dot(sum_vx, sum_vx) - sum_vx_sq)
        
        return self.w0 + linear + interaction
    
    def predict(self, X):
        """预测"""
        predictions = []
        for x in X:
            predictions.append(self._predict_single(x))
        return np.array(predictions)

隐式反馈处理

显式反馈 vs 隐式反馈

  • 显式反馈：用户明确给出的评分（ 1-5 星）、点赞、收藏等
  • 隐式反馈：用户行为数据，如点击、浏览时长、购买等

隐式反馈的特点

  1. 数据量大：隐式反馈比显式反馈多得多
  2. 噪声大：点击不代表喜欢，可能是误点
  3. 只有正样本：没有明确的负样本（未点击不代表不喜欢）

隐式反馈的处理方法

1. 加权矩阵分解（ Weighted MF）

给不同的隐式反馈赋予不同的权重：

其中 是置信度权重，通常： - 点击次数越多，权重越大 - 浏览时长越长，权重越大

2. 负样本采样

从未交互的物品中采样负样本，与正样本配对训练。

3. 使用 BPR

BPR 天然适合隐式反馈，因为它只需要正样本和负样本的对比。

隐式反馈代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
class ImplicitFeedbackMF:
    def __init__(self, n_factors=50, learning_rate=0.01, reg=0.01, n_epochs=20):
        """隐式反馈矩阵分解"""
        self.n_factors = n_factors
        self.learning_rate = learning_rate
        self.reg = reg
        self.n_epochs = n_epochs
        self.user_factors = None
        self.item_factors = None
        
    def fit(self, user_item_interactions, confidence_func=None):
        """
        训练模型
        
        Parameters:
        -----------
        user_item_interactions : dict
            {user_id: {item_id: interaction_count }}
        confidence_func : callable, optional
            置信度函数，将交互次数转换为置信度
        """
        if confidence_func is None:
            # 默认置信度函数： c = 1 + alpha * log(1 + count)
            confidence_func = lambda count: 1 + 10 * np.log1p(count)
        
        users = list(user_item_interactions.keys())
        items = set()
        for items_dict in user_item_interactions.values():
            items.update(items_dict.keys())
        items = list(items)
        
        self.user_to_idx = {user: idx for idx, user in enumerate(users)}
        self.idx_to_user = {idx: user for idx, user in enumerate(users)}
        self.item_to_idx = {item: idx for idx, item in enumerate(items)}
        self.idx_to_item = {idx: item for idx, item in enumerate(items)}
        
        n_users = len(users)
        n_items = len(items)
        
        # 初始化
        self.user_factors = np.random.normal(scale=0.1, size=(n_users, self.n_factors))
        self.item_factors = np.random.normal(scale=0.1, size=(n_items, self.n_factors))
        
        # 构建训练样本（带置信度）
        samples = []
        for user_id, items_dict in user_item_interactions.items():
            user_idx = self.user_to_idx[user_id]
            for item_id, count in items_dict.items():
                item_idx = self.item_to_idx[item_id]
                confidence = confidence_func(count)
                samples.append((user_idx, item_idx, confidence))
        
        # 训练
        for epoch in range(self.n_epochs):
            random.shuffle(samples)
            total_loss = 0
            
            for user_idx, item_idx, confidence in samples:
                # 预测（这里假设隐式反馈的目标值是 1）
                pred = np.dot(self.user_factors[user_idx], self.item_factors[item_idx])
                error = 1 - pred  # 目标值是 1
                
                # 更新参数（加权）
                user_factor = self.user_factors[user_idx].copy()
                item_factor = self.item_factors[item_idx].copy()
                
                self.user_factors[user_idx] += self.learning_rate * confidence * (
                    error * item_factor - self.reg * self.user_factors[user_idx]
                )
                self.item_factors[item_idx] += self.learning_rate * confidence * (
                    error * user_factor - self.reg * self.item_factors[item_idx]
                )
                
                total_loss += confidence * error ** 2
            
            if (epoch + 1) % 5 == 0:
                rmse = np.sqrt(total_loss / len(samples))
                print(f"Epoch {epoch + 1}, Weighted RMSE: {rmse:.4f}")
    
    def predict(self, user_id, item_id):
        """预测用户对物品的偏好"""
        if user_id not in self.user_to_idx or item_id not in self.item_to_idx:
            return 0
        
        user_idx = self.user_to_idx[user_id]
        item_idx = self.item_to_idx[item_id]
        pred = np.dot(self.user_factors[user_idx], self.item_factors[item_idx])
        return pred
    
    def recommend(self, user_id, n=10):
        """推荐物品"""
        if user_id not in self.user_to_idx:
            return []
        
        predictions = []
        for item_idx in range(len(self.item_factors)):
            item_id = self.idx_to_item[item_idx]
            pred = self.predict(user_id, item_id)
            predictions.append((item_id, pred))
        
        predictions.sort(key=lambda x: x[1], reverse=True)
        return predictions[:n]

常见问题解答（ Q&A）

Q1: User-CF 和 Item-CF 应该选择哪个？

A: 选择取决于具体场景：

  • Item-CF 更常用：物品数量通常少于用户数量，计算成本更低；物品相似度更稳定，可以预先计算；推荐结果更稳定。
  • User-CF 适合的场景：用户数量相对较少；用户兴趣变化快，需要实时捕捉；希望发现用户潜在兴趣。

实际建议：大多数情况下选择 Item-CF，除非有特殊需求。

Q2: 矩阵分解的潜在特征维度 如何选择？

A: 的选择需要权衡：

  • 太小：模型表达能力不足，欠拟合
  • 太大：容易过拟合，计算成本高

经验法则： - 小规模数据（< 10 万用户）： - 中等规模（ 10 万-100 万用户）： - 大规模（> 100 万用户）： 实践方法：使用交叉验证，在验证集上测试不同的 值，选择 RMSE/NDCG 最优的。

Q3: 如何处理冷启动问题？

A: 冷启动分为用户冷启动和物品冷启动：

用户冷启动： - 利用用户注册信息（年龄、性别、地域）初始化用户向量 - 使用热门物品推荐作为默认策略 - 引导用户进行兴趣标注

物品冷启动： - 利用物品内容特征（类别、标签）初始化物品向量 - 使用内容相似度推荐相似物品 - 利用物品的发布者、发布时间等信息

混合策略：冷启动阶段使用内容推荐，积累数据后切换到协同过滤。

Q4: SGD 和 ALS 哪个更好？

A: 各有优劣：

SGD： - 优点：实现简单，内存占用小，适合在线学习 - 缺点：收敛慢，难以并行化

ALS： - 优点：收敛快，可并行化，适合大规模数据 - 缺点：内存占用大（需要存储矩阵），不适合在线学习

选择建议： - 小规模数据： SGD - 大规模数据： ALS（ Spark MLlib） - 在线学习： SGD

Q5: 为什么 BPR 比传统的评分预测方法效果好？

A: BPR 的优势在于：

  1. 直接优化排序指标： BPR 优化的是排序（ AUC），而不是评分预测的 RMSE，更符合推荐任务的目标
  2. 适合隐式反馈：只需要正样本和负样本的对比，不需要精确的评分
  3. 个性化更强：每个用户的排序是独立的，不会受到其他用户评分的影响

实验证明：在隐式反馈场景下， BPR 的 AUC 通常比 MF 高 5-10%。

Q6: 如何处理数据稀疏性问题？

A: 数据稀疏性是推荐系统的核心挑战：

  1. 矩阵分解：将高维稀疏矩阵分解为低维稠密矩阵，是解决稀疏性的有效方法
  2. 正则化：防止过拟合，提高泛化能力
  3. 利用隐式反馈：隐式反馈数据量大，可以补充显式反馈
  4. 特征工程：利用用户和物品的辅助信息（如类别、标签）
  5. 降维技术： PCA 、 SVD 等降维方法

Q7: 偏置项的作用是什么？

A: 偏置项捕捉了评分中的系统性偏差：

  • 用户偏置 ：捕捉用户的评分习惯（有些用户习惯打高分，有些习惯打低分）
  • 物品偏置 ：捕捉物品的受欢迎程度（热门物品平均分高）
  • 全局偏置 ：整体评分水平

实验证明：加入偏置项后， RMSE 通常可以降低 10-20%。

Q8: SVD++ 中的隐式反馈如何构建？

A: 隐式反馈可以从多种用户行为中提取：

  1. 浏览行为：用户浏览过但未评分的物品
  2. 点击行为：用户点击过的物品
  3. 购买行为：用户购买过的物品（即使未评分）
  4. 收藏行为：用户收藏的物品
  5. 观看时长：视频/音频的观看时长超过阈值

注意：隐式反馈需要归一化，通常使用 作为归一化因子。

Q9: FM 和矩阵分解的关系是什么？

A: FM 是矩阵分解的推广：

  • 矩阵分解：只考虑用户-物品交互，特征向量是 one-hot 编码
  • FM：可以同时考虑用户特征、物品特征和交互特征，更灵活

数学关系：如果 FM 的特征向量只包含用户和物品的 one-hot 编码，则 FM 退化为矩阵分解。

FM 的优势：可以融合更多特征（如用户年龄、物品类别），提高推荐效果。

Q10: 如何评估推荐系统的效果？

A: 推荐系统的评估指标分为两类：

离线指标： - 评分预测： RMSE 、 MAE - 排序： AUC 、 NDCG 、 Precision@K 、 Recall@K

在线指标： - 点击率（ CTR）：推荐物品的点击率 - 转化率：推荐物品的购买/转化率 - 用户留存率：使用推荐系统后的用户留存

实践建议：离线指标用于模型选择和调参，在线 A/B 测试用于最终验证。

Q11: 矩阵分解的初始化方法有哪些？

A: 常见的初始化方法：

  1. 随机初始化：从正态分布 采样
  2. Xavier 初始化：，其中 是输入维度
  3. 预训练初始化：使用其他模型（如 Item-CF）的相似度矩阵初始化
  4. 均值初始化：用用户/物品的平均评分初始化偏置项

建议：通常使用随机初始化，配合学习率衰减。

Q12: 如何处理评分预测的边界问题？

A: 评分预测可能超出有效范围（如 1-5 分）：

  1. 截断：预测值限制在 范围内
  2. Sigmoid 映射：使用 sigmoid 函数将预测值映射到 3. 不处理：如果超出范围的比例很小，可以不处理

实践：大多数情况下，截断是最简单有效的方法。

Q13: 如何加速矩阵分解的训练？

A: 加速方法：

  1. 使用 ALS： ALS 可以并行化，比 SGD 快
  2. 负采样：在 BPR 中，只采样部分负样本
  3. 特征降维：减少潜在特征维度 4. 批量更新：使用 mini-batch SGD
  4. 使用 GPU：利用 GPU 加速矩阵运算
  5. 分布式训练：使用 Spark 、 TensorFlow 等分布式框架

Q14: 矩阵分解的过拟合问题如何解决？

A: 防止过拟合的方法：

  1. 正则化： L2 正则化 2. 早停（ Early Stopping）：在验证集上监控性能，性能不再提升时停止
  2. Dropout：随机丢弃部分特征（在深度学习中常用）
  3. 减少特征维度：降低 值
  4. 增加训练数据：更多的训练样本有助于泛化

建议：正则化是最常用的方法，通常设置在 之间。

Q15: 如何实现实时推荐？

A: 实时推荐的实现策略：

  1. 增量更新：使用在线学习算法（如 SGD），新数据到来时增量更新模型
  2. 缓存机制：预先计算热门用户的推荐结果，缓存起来
  3. 特征缓存：缓存用户和物品的特征向量，避免重复计算
  4. 流式处理：使用 Kafka 、 Flink 等流处理框架实时处理用户行为
  5. 混合策略：离线模型 + 在线规则，离线模型定期更新，在线规则实时调整

架构：通常采用 Lambda 架构，离线批处理 + 在线流处理。

总结

本文深入讲解了协同过滤和矩阵分解的核心算法：

  1. 协同过滤： User-CF 和 Item-CF 的基本原理、相似度计算、代码实现
  2. 矩阵分解：基础 MF 、带偏置 MF 、 SVD++ 的数学原理和实现
  3. 优化方法： SGD 和 ALS 的对比和选择
  4. 排序学习： BPR 从评分预测到排序学习的转变
  5. 因子分解机： FM 处理稀疏特征的能力
  6. 隐式反馈：如何处理隐式反馈数据
  7. 实践技巧：偏置项、正则化、冷启动等

这些算法是推荐系统的基础，理解它们有助于学习更高级的深度学习方法。在实际应用中，需要根据数据规模、业务场景选择合适的算法，并通过实验验证效果。

参考文献

  1. Koren, Y., Bell, R., & Volinsky, C. (2009). Matrix factorization techniques for recommender systems. Computer, 42(8), 30-37. IEEE
  2. Rendle, S., Freudenthaler, C., Gantner, Z., & Schmidt-Thieme, L. (2009). BPR: Bayesian personalized ranking from implicit feedback. UAI. arXiv:1205.2618
  3. Rendle, S. (2010). Factorization machines. ICDM. DOI:10.1109/ICDM.2010.127
  4. Koren, Y. (2008). Factorization meets the neighborhood: a multifaceted collaborative filtering model. KDD. DOI:10.1145/1401890.1401944
  5. Hu, Y., Koren, Y., & Volinsky, C. (2008). Collaborative filtering for implicit feedback datasets. ICDM. DOI:10.1109/ICDM.2008.22
  • 本文标题：推荐系统（二）—— 协同过滤与矩阵分解
  • 本文作者：Chen Kai
  • 创建时间：2024-05-07 14:30:00
  • 本文链接：https://www.chenk.top/%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%EF%BC%88%E4%BA%8C%EF%BC%89%E2%80%94%E2%80%94-%E5%8D%8F%E5%90%8C%E8%BF%87%E6%BB%A4%E4%B8%8E%E7%9F%A9%E9%98%B5%E5%88%86%E8%A7%A3/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
 评论