推荐系统（九）—— 多任务学习与多目标优化
Chen Kai BOSS
  2024-06-11 09:45:00 2024-06-11 09:45      23k 字  90 分钟  

在推荐系统的实际应用中，我们往往需要同时优化多个目标：点击率（ CTR）、转化率（ CVR）、停留时长、点赞、评论、分享等。传统的单任务学习模型为每个目标单独训练一个模型，这不仅增加了模型维护成本，还忽略了任务之间的关联性。多任务学习（ Multi-Task Learning, MTL）通过共享底层特征表示，让多个任务共同学习，既能提升模型性能，又能降低计算和存储成本。

多任务学习在推荐系统中已经得到了广泛应用。阿里巴巴的 ESMM 模型解决了 CVR 预估中的样本选择偏差问题， Google 的 MMoE 模型通过多门控机制实现了任务间的灵活共享，腾讯的 PLE 模型进一步解决了负迁移问题。这些模型在工业实践中都取得了显著的效果提升： ESMM 在淘宝的 CVR 预估中提升了 2.18%， MMoE 在 YouTube 推荐中提升了多个指标的离线效果， PLE 在腾讯视频推荐中相比 MMoE 提升了 0.39%的 AUC 。

然而，多任务学习并非简单的"共享参数就能提升性能"。任务之间的关系复杂：有些任务高度相关（如 CTR 和 CVR），有些任务存在冲突（如点击率和停留时长），有些任务数据分布差异巨大（如 CTR 样本量是 CVR 的 100 倍）。如何设计合适的网络架构、如何平衡不同任务的损失、如何处理负迁移问题，都是多任务学习中的核心挑战。

本文系统梳理多任务学习在推荐系统中的应用。我们将从多任务学习的动机开始，理解为什么需要多任务学习；然后深入 Shared-Bottom 、 ESMM 、 MMoE 、 PLE 等经典架构；接着探讨负迁移问题、任务关系建模、损失平衡策略等关键技术；最后通过完整的代码实现和工业实践案例，帮助读者掌握多任务学习的核心技术和实践方法。无论你是多任务学习的新手，还是想系统掌握工业级多任务推荐模型，这篇文章都能帮你建立完整的知识体系。

多任务学习的动机

推荐系统中的多目标问题

在推荐系统中，我们通常需要同时优化多个业务指标：

点击率（ CTR）：用户点击推荐物品的概率，直接影响推荐系统的曝光效果。

转化率（ CVR）：用户点击后发生转化（购买、下载、注册等）的概率，直接影响业务收益。

停留时长：用户在推荐内容上的停留时间，反映内容质量和用户兴趣。

互动行为：点赞、评论、分享、收藏等，反映用户对内容的深度参与。

长期价值：用户留存、复购、生命周期价值等，反映推荐系统的长期影响。

这些目标之间存在复杂的关系： CTR 和 CVR 是顺序关系（先点击后转化），停留时长和互动行为可能正相关，但 CTR 和停留时长可能存在冲突（高 CTR 可能带来低停留时长）。传统的单任务学习为每个目标单独训练模型，存在以下问题：

模型维护成本高：每个任务需要独立的模型、特征工程、训练流程和线上服务，维护成本随任务数量线性增长。

特征表示不共享：不同任务的模型学习到的特征表示可能不一致，无法利用任务间的关联性。

数据利用不充分：某些任务（如 CVR）的样本量远小于其他任务（如 CTR），单独训练容易过拟合。

线上服务复杂：需要同时部署多个模型，推理延迟和资源消耗都较高。

多任务学习的优势

多任务学习通过共享底层特征表示，让多个任务共同学习，具有以下优势：

提升模型性能：通过任务间的知识共享，每个任务都能从其他任务中学习到有用的特征表示，特别是在数据稀疏的任务上效果更明显。

降低模型复杂度：共享底层参数，减少了总参数量，降低了过拟合风险。

提高训练效率：一次训练可以同时优化多个目标，比单独训练多个模型更高效。

简化线上服务：只需要部署一个模型，降低了服务复杂度和资源消耗。

更好的泛化能力：多任务学习相当于一种正则化，提高了模型的泛化能力。

多任务学习的挑战

尽管多任务学习有诸多优势，但在实际应用中仍面临挑战：

任务关系复杂：任务之间可能相关、冲突或独立，如何建模任务关系是多任务学习的核心问题。

负迁移问题：当任务之间存在冲突时，共享参数可能导致某些任务性能下降，这就是负迁移（ Negative Transfer）。

损失平衡困难：不同任务的损失尺度、梯度大小、优化难度都不同，如何平衡多个任务的损失是关键技术。

样本分布差异：不同任务的样本量、正负样本比例、数据分布都不同，需要合适的采样和加权策略。

架构设计复杂：如何在共享和独立之间找到平衡，设计合适的网络架构是多任务学习的关键。

Shared-Bottom 架构：多任务学习的基础

架构设计

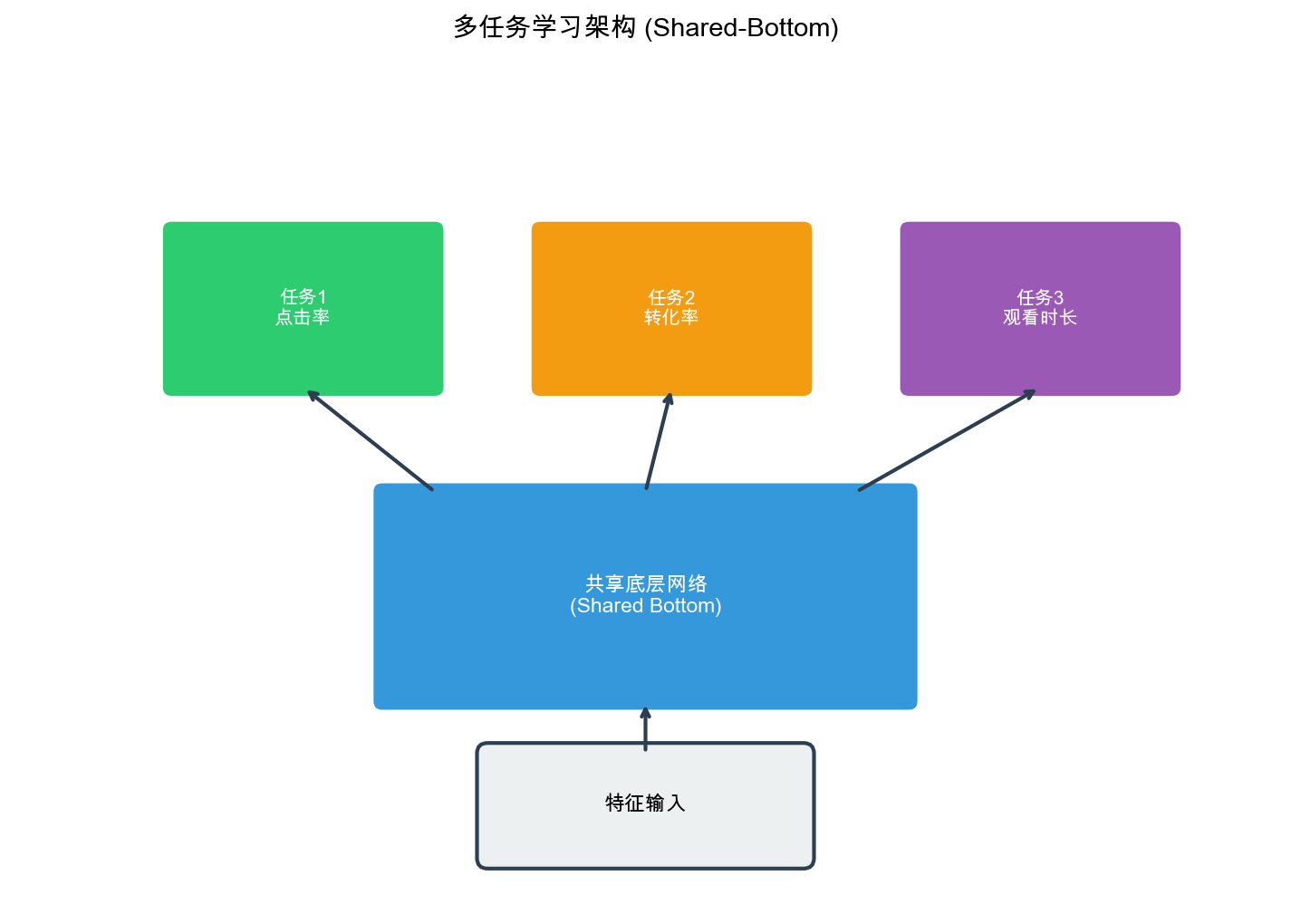
Shared-Bottom 架构是多任务学习最基础的架构，基本思路：多个任务共享底层特征表示（ Shared Bottom），每个任务有独立的顶层网络（ Task-Specific Tower）。

共享底层网络将输入特征 映射为共享表示：

每个任务的顶层网络基于共享表示 进行预测：

Extra close brace or missing open brace\hat{y}_i = f_i(\mathbf{h}), \quad i \in \{1, 2, \dots, T}

其中 是共享的底层网络， 是第 个任务的顶层网络， 是任务数量。

数学原理

Shared-Bottom 架构的损失函数为多个任务损失的加权和：

$$

L = _{i=1}^T w_i L_i(_i, y_i)$$

其中 是第 个任务的权重， 是第 个任务的损失函数。

在反向传播时，共享参数的梯度是多个任务梯度的加权和：

这意味着共享参数会同时受到多个任务的影响，学习到的特征表示需要同时满足多个任务的需求。

代码实现

下面我们实现一个完整的 Shared-Bottom 多任务学习模型。这个实现的基本思路：所有任务共享一个底层特征提取网络，然后每个任务有自己独立的预测塔。这样做的好处是可以让不同任务在学习底层特征时相互帮助，特别是当某些任务的数据较少时，可以借助其他任务的数据学习到更好的特征表示。

在实际应用中，共享底层通常是一个多层的全连接网络（也可以是 CNN 、 Transformer 等），它将原始输入特征映射到一个共享的隐藏空间。每个任务的预测塔也是一个多层网络，它基于共享表示进行任务特定的预测。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
import torch
import torch.nn as nn
import torch.nn.functional as F

class SharedBottom(nn.Module):
    """
    Shared-Bottom 多任务学习架构
    
    这是最基础的多任务学习架构，所有任务共享底层特征提取器。
    适用于任务高度相关的场景，如 CTR 和 CVR 预估。
    """
    
    def __init__(self, input_dim, shared_hidden_dims, task_hidden_dims, num_tasks, dropout=0.1):
        """
        初始化 Shared-Bottom 模型
        
        Args:
            input_dim: 输入特征维度，例如 1000 维的用户和物品特征
            shared_hidden_dims: 共享层隐藏层维度列表，如[512, 256]
                               表示两层全连接网络，维度依次为 512 和 256
            task_hidden_dims: 任务塔隐藏层维度列表，如[128, 64]
                             每个任务塔都有相同的架构
            num_tasks: 任务数量，例如 2 表示 CTR 和 CVR 两个任务
            dropout: Dropout 比率，用于防止过拟合，通常设置为 0.1-0.3
        """
        super(SharedBottom, self).__init__()
        self.num_tasks = num_tasks  # 保存任务数量，用于后续处理
        
        # 构建共享底层网络
        # 这个网络将被所有任务共享，是多任务学习的核心
        shared_layers = []
        prev_dim = input_dim  # 记录上一层的输出维度
        
        # 遍历每一层的隐藏维度，构建多层网络
        for hidden_dim in shared_hidden_dims:
            # 添加线性变换层： prev_dim -> hidden_dim
            shared_layers.append(nn.Linear(prev_dim, hidden_dim))
            # 添加 ReLU 激活函数，引入非线性
            shared_layers.append(nn.ReLU())
            # 添加 Dropout 层，随机丢弃部分神经元，防止过拟合
            shared_layers.append(nn.Dropout(dropout))
            # 更新 prev_dim 为当前层的输出维度
            prev_dim = hidden_dim
        
        # 使用 Sequential 将所有层组合成一个模块
        self.shared_bottom = nn.Sequential(*shared_layers)
        
        # 构建任务特定塔（每个任务一个）
        # 任务塔接收共享底层的输出，进行任务特定的预测
        self.task_towers = nn.ModuleList()  # 使用 ModuleList 存储多个任务塔
        
        for _ in range(num_tasks):
            tower_layers = []
            # 任务塔的输入维度是共享底层的输出维度
            prev_dim = shared_hidden_dims[-1]
            
            # 构建任务塔的隐藏层
            for hidden_dim in task_hidden_dims:
                tower_layers.append(nn.Linear(prev_dim, hidden_dim))
                tower_layers.append(nn.ReLU())
                tower_layers.append(nn.Dropout(dropout))
                prev_dim = hidden_dim
            
            # 最后一层输出单个预测值（例如点击概率）
            # 注意：这里输出的是 logit，不是概率（未经过 sigmoid）
            tower_layers.append(nn.Linear(prev_dim, 1))
            
            # 将当前任务塔添加到 ModuleList
            self.task_towers.append(nn.Sequential(*tower_layers))
    
    def forward(self, x):
        """
        前向传播
        
        Args:
            x: 输入特征， shape 为[batch_size, input_dim]
               batch_size 是批次大小， input_dim 是特征维度
        
        Returns:
            outputs: 各任务的输出， list of [batch_size, 1]
                    每个任务返回一个预测值（ logit）
        """
        # 第一步：通过共享底层网络提取特征
        # 这一步所有任务共享，学习通用的特征表示
        shared_output = self.shared_bottom(x)  # shape: [batch_size, shared_hidden_dims[-1]]
        
        # 第二步：每个任务基于共享特征进行独立预测
        outputs = []
        for tower in self.task_towers:
            # 将共享特征输入到任务塔，得到该任务的预测
            output = tower(shared_output)  # shape: [batch_size, 1]
            outputs.append(output)
        
        # 返回所有任务的预测结果
        return outputs

# 使用示例
# 创建一个 Shared-Bottom 模型，用于 CTR 和 CVR 两个任务
model = SharedBottom(
    input_dim=1000,              # 输入特征维度为 1000
    shared_hidden_dims=[512, 256],  # 共享底层： 1000 -> 512 -> 256
    task_hidden_dims=[128, 64],     # 任务塔： 256 -> 128 -> 64 -> 1
    num_tasks=2,                    # 2 个任务（ CTR 和 CVR）
    dropout=0.1                     # Dropout 比率 0.1
)

# 前向传播示例
# 创建一个 batch 的输入数据： 32 个样本，每个样本 1000 维特征
x = torch.randn(32, 1000)
outputs = model(x)

# 输出每个任务的预测结果形状
print(f"Task 1 output shape: {outputs[0].shape}")  # 输出： torch.Size([32, 1])
print(f"Task 2 output shape: {outputs[1].shape}")  # 输出： torch.Size([32, 1])

代码关键点解析：

  1. 共享底层的作用：共享底层网络是所有任务的"公共知识库"，它学习的特征表示需要同时满足所有任务的需求。这要求任务之间有一定的相关性，否则共享可能导致负迁移。

  2. 任务塔的独立性：虽然底层是共享的，但每个任务有独立的预测塔。这些塔可以学习任务特定的模式，例如 CTR 塔学习"什么样的特征容易被点击"， CVR 塔学习"什么样的特征容易转化"。

  3. 参数量分析：假设输入维度 1000，共享层[512, 256]，任务塔[128, 64]， 2 个任务。共享部分参数量约为： 1000 × 512 + 512 × 256 ≈ 643K 。每个任务塔参数量约为： 256 × 128 + 128 × 64 + 64 × 1 ≈ 41K 。总参数量约为： 643K + 2 × 41K = 725K 。相比于两个独立模型（约 1.4M 参数），参数量减少了约 48%。

  4. 梯度流动：在反向传播时，共享底层的梯度来自所有任务。如果任务 1 的梯度是，任务 2 的梯度是，则共享参数的总梯度是（可能带权重）。这意味着共享参数的更新需要平衡所有任务的需求。

  5. 潜在问题：当任务冲突时（例如梯度方向相反），共享底层可能学不好。这时需要考虑 MMoE 或 PLE 等更灵活的架构。

Shared-Bottom 的局限性

Shared-Bottom 架构虽然简单有效，但存在明显的局限性：

任务关系假设过强：假设所有任务都高度相关，共享所有底层参数。当任务之间存在冲突时，共享参数可能导致负迁移。

灵活性不足：所有任务共享相同的底层表示，无法根据任务特点进行差异化处理。

难以处理任务差异：当任务的样本量、数据分布、优化难度差异很大时， Shared-Bottom 难以平衡不同任务的需求。

ESMM：解决 CVR 预估的样本选择偏差

问题背景

在电商推荐系统中， CVR（转化率）预估是一个关键任务。 CVR 定义为：用户点击后发生转化（购买、下载等）的概率：

$$

CVR = P( | ) = {} $$

然而， CVR 预估面临一个严重的问题：样本选择偏差（ Sample Selection Bias）。

样本选择偏差的原因： - CVR 模型只在点击样本上训练（只有点击的用户才能转化） - 但线上推理时需要在所有曝光样本上预测（包括未点击的样本） - 训练分布和推理分布不一致，导致模型性能下降

数据稀疏问题： - CTR 样本量通常是 CVR 的 10-100 倍 - CVR 样本极度稀疏，单独训练容易过拟合

ESMM 架构设计

ESMM（ Entire Space Multi-Task Model）通过多任务学习解决了 CVR 预估的样本选择偏差问题。 ESMM 的基本思路：

利用 CTR 和 CTCVR 的完整空间： - CTR：，在所有曝光样本上训练 - CTCVR：，也在所有曝光样本上训练 - CVR：，通过 CTCVR / CTR 间接计算

数学关系： $$

P( | ) = P( | ) P( | )$$

即： $$

CTCVR = CTR CVR$$

ESMM 同时预测 CTR 和 CTCVR，然后通过除法得到 CVR：

$$

CVR = $$

其中 是一个很小的常数，防止除零。

网络架构

ESMM 的网络架构包含： - 共享底层：共享的特征提取层 - CTR 塔：预测点击率 - CVR 塔：预测转化率（但只在点击样本上有标签） - CTCVR：通过 CTR 和 CVR 的乘积计算

下面我们实现 ESMM（ Entire Space Multi-Task Model）。 ESMM 的核心创新在于通过巧妙的多任务建模解决 CVR 预估中的样本选择偏差问题。

问题背景：传统的 CVR 模型只在点击样本上训练（因为只有点击的用户才可能转化），但在推理时需要在所有曝光样本上预测。这导致训练和推理的数据分布不一致，产生样本选择偏差。

ESMM 的解决方案：不直接预测 CVR，而是同时预测 CTR 和 CTCVR 两个辅助任务，然后通过 间接得到 CVR 。由于 CTR 和 CTCVR 都在完整空间（所有曝光样本）上训练，避免了样本选择偏差。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
class ESMM(nn.Module):
    """
    ESMM: Entire Space Multi-Task Model for CVR Prediction
    
    ESMM 通过同时建模 CTR 和 CTCVR 两个任务，解决 CVR 预估中的样本选择偏差问题。
    核心公式： CTCVR = CTR × CVR，因此 CVR = CTCVR / CTR
    """
    
    def __init__(self, input_dim, shared_hidden_dims, tower_hidden_dims, dropout=0.1):
        """
        初始化 ESMM 模型
        
        Args:
            input_dim: 输入特征维度
            shared_hidden_dims: 共享层隐藏层维度列表，如[256, 128]
            tower_hidden_dims: 任务塔隐藏层维度列表，如[64, 32]
            dropout: Dropout 比率
        """
        super(ESMM, self).__init__()
        
        # 共享底层网络
        # CTR 塔和 CVR 塔共享这个底层网络，可以相互学习特征
        shared_layers = []
        prev_dim = input_dim
        for hidden_dim in shared_hidden_dims:
            shared_layers.append(nn.Linear(prev_dim, hidden_dim))
            shared_layers.append(nn.ReLU())
            shared_layers.append(nn.Dropout(dropout))
            prev_dim = hidden_dim
        self.shared_bottom = nn.Sequential(*shared_layers)
        
        # CTR 塔：预测点击率 P(click | impression)
        # 这个塔在所有曝光样本上训练
        ctr_layers = []
        prev_dim = shared_hidden_dims[-1]
        for hidden_dim in tower_hidden_dims:
            ctr_layers.append(nn.Linear(prev_dim, hidden_dim))
            ctr_layers.append(nn.ReLU())
            ctr_layers.append(nn.Dropout(dropout))
            prev_dim = hidden_dim
        # 最后一层输出 logit，然后通过 Sigmoid 映射到(0, 1)
        ctr_layers.append(nn.Linear(prev_dim, 1))
        ctr_layers.append(nn.Sigmoid())  # 输出概率值
        self.ctr_tower = nn.Sequential(*ctr_layers)
        
        # CVR 塔：预测转化率 P(conversion | click)
        # 注意：这个塔并不直接用于计算损失，而是通过 CTCVR = CTR * CVR 间接监督
        cvr_layers = []
        prev_dim = shared_hidden_dims[-1]
        for hidden_dim in tower_hidden_dims:
            cvr_layers.append(nn.Linear(prev_dim, hidden_dim))
            cvr_layers.append(nn.ReLU())
            cvr_layers.append(nn.Dropout(dropout))
            prev_dim = hidden_dim
        cvr_layers.append(nn.Linear(prev_dim, 1))
        cvr_layers.append(nn.Sigmoid())  # 输出概率值
        self.cvr_tower = nn.Sequential(*cvr_layers)
    
    def forward(self, x):
        """
        ESMM 的前向传播
        
        Args:
            x: 输入特征， shape 为[batch_size, input_dim]
        
        Returns:
            ctr: CTR 预测值， shape 为[batch_size, 1]，范围(0, 1)
            cvr: CVR 预测值， shape 为[batch_size, 1]，范围(0, 1)
            ctcvr: CTCVR 预测值， shape 为[batch_size, 1]，范围(0, 1)
        """
        # 第一步：提取共享特征
        shared_output = self.shared_bottom(x)
        
        # 第二步：预测 CTR（点击率）
        # 在所有曝光样本上计算，有直接的监督信号
        ctr = self.ctr_tower(shared_output)  # P(click | impression)
        
        # 第三步：预测 CVR（转化率）
        # 虽然只有点击样本有 CVR 标签，但通过 CTCVR 间接监督
        cvr = self.cvr_tower(shared_output)  # P(conversion | click)
        
        # 第四步：计算 CTCVR（点击后转化率）
        # 关键公式： P(conversion | impression) = P(click | impression) × P(conversion | click)
        # 即： CTCVR = CTR × CVR
        # 这个乘法操作是 ESMM 的核心，它将 CVR 的监督信号隐式地传递到完整空间
        ctcvr = ctr * cvr  # P(conversion | impression)
        
        return ctr, cvr, ctcvr

# ESMM 的损失函数
def esmm_loss(ctr_pred, cvr_pred, ctcvr_pred, ctr_label, cvr_label, ctcvr_label):
    """
    ESMM 的损失函数
    
    关键点：
    1. CTR 损失在所有曝光样本上计算
    2. CTCVR 损失也在所有曝光样本上计算
    3. CVR 没有直接的损失，而是通过 CTCVR = CTR × CVR 的约束间接优化
    
    Args:
        ctr_pred: CTR 预测值， shape 为[batch_size, 1]
        cvr_pred: CVR 预测值， shape 为[batch_size, 1]（实际不用于损失计算）
        ctcvr_pred: CTCVR 预测值， shape 为[batch_size, 1]
        ctr_label: CTR 标签， shape 为[batch_size, 1]， 1 表示点击， 0 表示未点击
        cvr_label: CVR 标签（实际不用于损失计算）
        ctcvr_label: CTCVR 标签， shape 为[batch_size, 1]， 1 表示点击且转化， 0 表示其他
    
    Returns:
        total_loss: 总损失
        ctr_loss: CTR 任务的损失
        ctcvr_loss: CTCVR 任务的损失
    """
    # CTR 损失：在所有曝光样本上计算
    # 对于每个样本，预测是否会被点击
    ctr_loss = F.binary_cross_entropy(ctr_pred, ctr_label)
    
    # CTCVR 损失：在所有曝光样本上计算
    # 对于每个样本，预测是否会点击并转化
    # 关键：即使是未点击的样本， CTCVR 标签也是明确的（为 0）
    # 这样 CVR 塔就能在完整空间上接收到监督信号，避免样本选择偏差
    ctcvr_loss = F.binary_cross_entropy(ctcvr_pred, ctcvr_label)
    
    # 总损失：两个任务的损失相加
    # 可以根据实际情况调整权重： total_loss = w1 * ctr_loss + w2 * ctcvr_loss
    total_loss = ctr_loss + ctcvr_loss
    
    return total_loss, ctr_loss, ctcvr_loss

ESMM 的关键技术细节：

  1. 完整空间建模： CTR 和 CTCVR 都在所有曝光样本上计算损失，这是避免样本选择偏差的关键。对于未点击的样本， CTR 标签为 0， CTCVR 标签也为 0（未点击就不可能转化）。

  2. 隐式 CVR 监督：虽然 CVR 塔没有直接的损失函数，但通过 的约束， CTCVR 的监督信号会反向传播到 CVR 塔。当 CTCVR 的预测不准确时，梯度会同时更新 CTR 塔和 CVR 塔。

  3. 推理时的 CVR 计算：在推理阶段，可以直接使用 CVR 塔的输出，或者使用 计算（ 是一个很小的常数，防止除零）。实践中通常直接使用 CVR 塔的输出，因为它已经通过 CTCVR 间接训练好了。

  4. 数据标签构造：

    • CTR 标签：所有曝光样本都有， 1 表示点击， 0 表示未点击
    • CVR 标签：理论上只有点击样本有，但在 ESMM 中我们不直接使用
    • CTCVR 标签：所有曝光样本都有， 1 表示点击且转化， 0 表示其他情况

  5. 优势分析：假设 CTR 样本量是 100 万，但只有 10 万次点击，其中 1 万次转化。传统 CVR 模型只能在 10 万点击样本上训练，而 ESMM 可以在 100 万曝光样本上训练 CTCVR 任务，大大增加了可用数据量。

ESMM 的优势

解决样本选择偏差： CTR 和 CTCVR 都在完整空间（所有曝光样本）上训练，避免了样本选择偏差。

利用 CTR 数据：通过共享底层参数， CVR 塔可以从 CTR 任务中学习有用的特征表示，缓解数据稀疏问题。

端到端训练： CTR 和 CTCVR 同时训练，保证了 CVR = CTCVR / CTR 的关系一致性。

ESMM 的局限性

假设 CTR 和 CVR 共享底层：当 CTR 和 CVR 的特征需求差异很大时，共享底层可能导致负迁移。

CVR 塔缺乏直接监督： CVR 塔只在点击样本上有标签，训练信号较弱。

除零问题：当 CTR 很小时， CVR = CTCVR / CTR 可能不稳定。

MMoE：多门控混合专家模型

动机：解决任务冲突问题

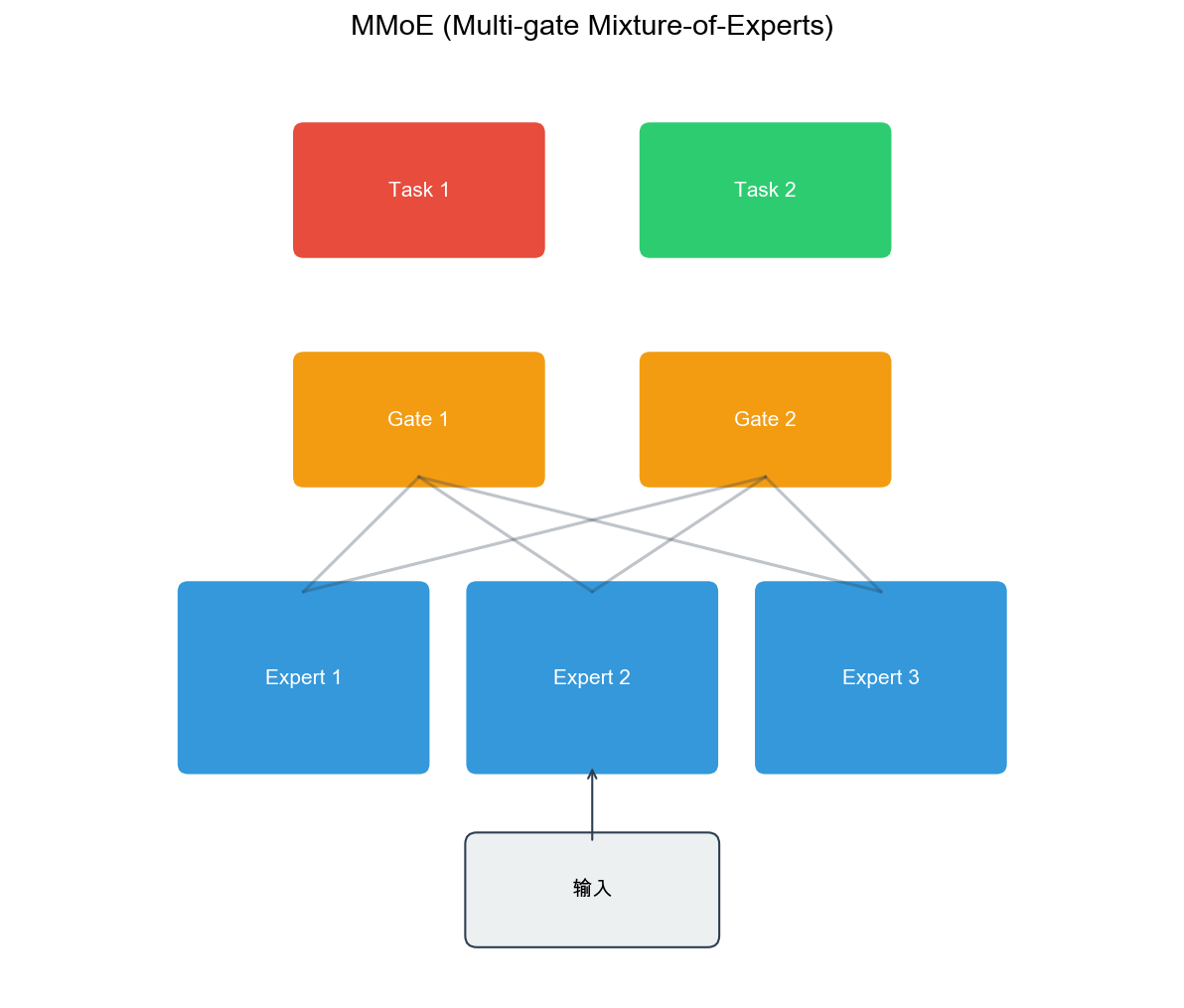
Shared-Bottom 架构假设所有任务高度相关，但当任务之间存在冲突时，共享参数可能导致负迁移。 MMoE（ Multi-gate Mixture-of-Experts）通过引入多个专家（ Expert）和门控网络（ Gate），让模型自动学习任务间的共享和独立关系。

架构设计

MMoE 的核心组件：

专家网络（ Expert）：多个独立的专家网络，每个专家学习不同的特征表示。

门控网络（ Gate）：每个任务有独立的门控网络，决定如何组合专家网络的输出。

任务塔（ Tower）：每个任务有独立的顶层网络，处理任务特定的特征。

数学表示：

Extra close brace or missing open brace\text{Expert 输出: } E_i(\mathbf{x}) = f_i(\mathbf{x}), \quad i \in \{1, 2, \dots, n_e} Extra close brace or missing open brace\text{门控权重: } g_k(\mathbf{x}) = \text{softmax}(W_k \mathbf{x} + b_k), \quad k \in \{1, 2, \dots, T} 任务输入 任务输出

其中 是专家数量， 是任务数量。

代码实现

MMoE（ Multi-gate Mixture-of-Experts）是 Google 提出的一个经典多任务学习架构。基本思路：使用多个专家网络学习不同的特征表示，每个任务通过独立的门控网络决定如何组合这些专家。这样，相关性高的任务可以共享相同的专家，而冲突的任务可以选择不同的专家，从而避免负迁移。

在实现时，需要注意以下几点： 1. 专家网络的数量通常设置为任务数量的 1-3 倍 2. 门控网络使用 Softmax 确保权重和为 1 3. 每个任务的输入是所有专家输出的加权和 4. 梯度可以通过门控权重反向传播到各个专家

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
class Expert(nn.Module):
    """
    专家网络
    
    每个专家是一个独立的多层全连接网络，学习特定的特征变换。
    不同的专家可能关注输入特征的不同方面。
    """
    
    def __init__(self, input_dim, hidden_dim, dropout=0.1):
        """
        Args:
            input_dim: 输入特征维度
            hidden_dim: 专家网络的输出维度
            dropout: Dropout 比率
        """
        super(Expert, self).__init__()
        # 构建一个两层的 MLP 作为专家网络
        # 也可以使用更深的网络或其他架构（如 ResNet 块）
        self.network = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),  # 第一层： input_dim -> hidden_dim
            nn.ReLU(),                         # 激活函数
            nn.Dropout(dropout),               # Dropout 防止过拟合
            nn.Linear(hidden_dim, hidden_dim), # 第二层： hidden_dim -> hidden_dim
            nn.ReLU(),
            nn.Dropout(dropout)
        )
    
    def forward(self, x):
        """
        Args:
            x: 输入特征， shape 为[batch_size, input_dim]
        Returns:
            输出特征， shape 为[batch_size, hidden_dim]
        """
        return self.network(x)

class Gate(nn.Module):
    """
    门控网络
    
    门控网络为每个任务生成一组权重，决定如何组合各个专家的输出。
    使用 Softmax 确保权重和为 1，可以理解为专家的"重要性分布"。
    """
    
    def __init__(self, input_dim, num_experts):
        """
        Args:
            input_dim: 输入特征维度（原始输入，不是专家输出）
            num_experts: 专家数量
        """
        super(Gate, self).__init__()
        # 门控网络通常是一个简单的线性变换 + Softmax
        # 也可以使用更复杂的网络，如多层 MLP
        self.gate_network = nn.Sequential(
            nn.Linear(input_dim, num_experts),  # 线性变换： input_dim -> num_experts
            nn.Softmax(dim=-1)                  # Softmax 确保权重和为 1
        )
    
    def forward(self, x):
        """
        Args:
            x: 输入特征， shape 为[batch_size, input_dim]
        Returns:
            门控权重， shape 为[batch_size, num_experts]
            每一行的权重和为 1
        """
        return self.gate_network(x)

class MMoE(nn.Module):
    """
    MMoE: Multi-gate Mixture-of-Experts
    
    MMoE 通过多个专家网络和门控机制，让每个任务自动学习如何组合专家，
    从而适应任务间的相关性和冲突，避免负迁移。
    """
    
    def __init__(self, input_dim, num_experts, expert_hidden_dim, 
                 task_hidden_dims, num_tasks, dropout=0.1):
        """
        初始化 MMoE 模型
        
        Args:
            input_dim: 输入特征维度
            num_experts: 专家数量，通常设置为任务数量的 1-3 倍
            expert_hidden_dim: 专家网络的输出维度
            task_hidden_dims: 任务塔隐藏层维度列表
            num_tasks: 任务数量
            dropout: Dropout 比率
        """
        super(MMoE, self).__init__()
        self.num_experts = num_experts
        self.num_tasks = num_tasks
        
        # 创建多个专家网络
        # 使用 ModuleList 确保专家网络的参数被正确注册
        self.experts = nn.ModuleList([
            Expert(input_dim, expert_hidden_dim, dropout)
            for _ in range(num_experts)
        ])
        
        # 为每个任务创建独立的门控网络
        # 这是 MMoE 的核心：不同任务有不同的门控，可以选择不同的专家组合
        self.gates = nn.ModuleList([
            Gate(input_dim, num_experts)
            for _ in range(num_tasks)
        ])
        
        # 为每个任务创建独立的预测塔
        self.task_towers = nn.ModuleList()
        for _ in range(num_tasks):
            tower_layers = []
            prev_dim = expert_hidden_dim  # 任务塔的输入是专家输出的加权和
            for hidden_dim in task_hidden_dims:
                tower_layers.append(nn.Linear(prev_dim, hidden_dim))
                tower_layers.append(nn.ReLU())
                tower_layers.append(nn.Dropout(dropout))
                prev_dim = hidden_dim
            tower_layers.append(nn.Linear(prev_dim, 1))  # 最后输出单个预测值
            self.task_towers.append(nn.Sequential(*tower_layers))
    
    def forward(self, x):
        """
        MMoE 的前向传播
        
        流程：
        1. 所有专家网络处理输入，得到多个专家输出
        2. 每个任务的门控网络计算专家权重
        3. 每个任务将专家输出加权求和，得到任务特定的输入
        4. 每个任务塔基于加权输入进行预测
        
        Args:
            x: 输入特征， shape 为[batch_size, input_dim]
        
        Returns:
            outputs: 各任务的输出， list of [batch_size, 1]
        """
        # 第一步：计算所有专家的输出
        # expert_outputs 是一个列表，每个元素 shape 为[batch_size, expert_hidden_dim]
        expert_outputs = []
        for expert in self.experts:
            expert_outputs.append(expert(x))
        
        # 将专家输出堆叠成一个 tensor，方便后续的加权求和
        # shape 变为：[batch_size, num_experts, expert_hidden_dim]
        expert_outputs = torch.stack(expert_outputs, dim=1)
        
        # 第二步：为每个任务计算输出
        outputs = []
        for i in range(self.num_tasks):
            # 第 2.1 步：计算当前任务的门控权重
            # gate_weights shape: [batch_size, num_experts]
            # 每一行表示该样本在当前任务下对各个专家的权重分配
            gate_weights = self.gates[i](x)
            
            # 第 2.2 步：加权组合专家输出
            # 将 gate_weights 扩展一个维度，方便与 expert_outputs 相乘
            # gate_weights shape: [batch_size, num_experts, 1]
            gate_weights = gate_weights.unsqueeze(-1)
            
            # 加权求和： expert_outputs * gate_weights 后在专家维度求和
            # 结果 shape: [batch_size, expert_hidden_dim]
            # 这是当前任务特定的输入，反映了该任务对不同专家的依赖
            task_input = (expert_outputs * gate_weights).sum(dim=1)
            
            # 第 2.3 步：通过任务塔进行预测
            output = self.task_towers[i](task_input)
            outputs.append(output)
        
        return outputs

# 使用示例
model = MMoE(
    input_dim=1000,           # 输入特征维度
    num_experts=4,            # 4 个专家网络
    expert_hidden_dim=256,    # 每个专家输出 256 维
    task_hidden_dims=[128, 64], # 任务塔： 256 -> 128 -> 64 -> 1
    num_tasks=2,              # 2 个任务
    dropout=0.1
)

# 前向传播示例
x = torch.randn(32, 1000)
outputs = model(x)
print(f"Task 1 output shape: {outputs[0].shape}")  # torch.Size([32, 1])
print(f"Task 2 output shape: {outputs[1].shape}")  # torch.Size([32, 1])

MMoE 的关键技术细节：

  1. 门控权重的含义：假设任务 1 的门控权重为[0.5, 0.3, 0.1, 0.1]，这意味着任务 1 主要依赖专家 1（ 50%）和专家 2（ 30%），较少依赖专家 3 和专家 4 。如果任务 2 的权重为[0.1, 0.1, 0.4, 0.4]，则说明两个任务关注不同的专家，可能学习不同的特征模式。

  2. 专家数量的选择：专家数量是一个重要的超参数。太少的专家可能无法捕获任务间的多样性，太多的专家会增加计算成本和过拟合风险。通常设置为：

    • 2 个任务： 3-6 个专家
    • 3-5 个任务： 4-8 个专家
    • 更多任务： 8-12 个专家

  3. 与 Shared-Bottom 的对比： Shared-Bottom 可以看作是 MMoE 的一个特例——只有 1 个专家，所有任务的门控权重都是 1 。 MMoE 通过增加专家数量和引入门控机制，提供了更大的灵活性。

  4. 梯度流动分析：在反向传播时，每个专家接收到的梯度是所有任务梯度的加权和，权重由门控网络决定。如果某个专家对任务 1 的权重是 0.8，对任务 2 的权重是 0.2，那么该专家的梯度主要来自任务 1 。

  5. 计算复杂度：假设输入维度$ d，专家数量 n_e，专家输出维度 h，任务数量 n_t。的参数量约为 d h，而的参数量约为 n_e d h + n_t d（专家参数门控参数）。当 n_e$ 较大时， MMoE 的参数量和计算量都会显著增加。

  6. 门控网络的设计变体：标准 MMoE 使用简单的线性门控，但也可以使用：

    • 多层 MLP 门控：提高门控的表达能力
    • 注意力机制：让门控权重依赖于输入的局部特征
    • 可学习的温度参数：控制 Softmax 的锐度

MMoE 的优势

灵活的任务关系建模：通过门控网络，每个任务可以自动学习如何组合专家，适应任务间的相关性和冲突。

避免负迁移：当任务冲突时，门控网络可以给冲突的专家分配低权重，减少负迁移。

参数效率：相比为每个任务单独训练模型， MMoE 共享专家网络，参数更少。

MMoE 的局限性

专家数量选择困难：专家数量需要人工设定，不同任务组合可能需要不同的专家数量。

门控网络可能退化：当任务高度相关时，门控网络可能退化为均匀分配，失去灵活性。

计算复杂度：相比 Shared-Bottom， MMoE 需要额外的门控网络计算。

PLE：渐进式分层提取

动机：解决负迁移和跷跷板现象

MMoE 虽然解决了任务冲突问题，但在实际应用中仍存在两个问题：

负迁移：当任务相关性较低时，共享专家可能导致某些任务性能下降。

跷跷板现象（ Seesaw Phenomenon）：优化一个任务时，另一个任务的性能下降，难以同时提升多个任务。

PLE（ Progressive Layered Extraction）通过引入任务特定专家（ Task-Specific Expert）和共享专家（ Shared Expert），并采用渐进式分层结构，进一步解决了这些问题。

架构设计

PLE 的核心思想：

任务特定专家 + 共享专家： - 每个任务有独立的专家网络（任务特定专家） - 所有任务共享部分专家网络（共享专家） - 通过门控网络决定如何组合

渐进式分层： - 底层：任务特定专家和共享专家 - 中层：可以进一步提取任务特定和共享特征 - 顶层：任务塔

数学表示（以两层为例）：

Extra close brace or missing open brace\text{底层共享专家: } E_s^1(\mathbf{x}) = \{e_{s,1}^1(\mathbf{x}), \dots, e_{s,n_s}^1(\mathbf{x})} Extra close brace or missing open brace\text{底层任务特定专家: } E_k^1(\mathbf{x}) = \{e_{k,1}^1(\mathbf{x}), \dots, e_{k,n_k}^1(\mathbf{x})} , \quad k \in \{1, \dots, T} 底层门控 底层输出 Extra close brace or missing open brace\text{中层共享专家: } E_s^2(\mathbf{h}_k^1) = \{e_{s,1}^2(\mathbf{h}_k^1), \dots, e_{s,n_s}^2(\mathbf{h}_k^1)} Extra close brace or missing open brace\text{中层任务特定专家: } E_k^2(\mathbf{h}_k^1) = \{e_{k,1}^2(\mathbf{h}_k^1), \dots, e_{k,n_k}^2(\mathbf{h}_k^1)} 中层门控 最终输出

代码实现

PLE（ Progressive Layered Extraction）是腾讯提出的改进架构，它解决了 MMoE 在任务相关性较低时的负迁移问题。 PLE 的核心创新是：引入任务特定专家（ Task-Specific Expert）和共享专家（ Shared Expert）的分离，并采用渐进式分层结构。

设计思路： 1. 每个任务有专属的专家网络，只为该任务服务，避免被其他任务的梯度"污染" 2. 保留共享专家，让任务间仍能学习公共知识 3. 多层渐进提取，让任务在不同抽象层次上进行不同程度的共享

这种设计在保持任务间知识共享的同时，给每个任务足够的独立性，有效缓解了跷跷板现象（优化一个任务导致另一个任务性能下降）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
class PLE(nn.Module):
    """
    PLE: Progressive Layered Extraction
    
    PLE 通过分离任务特定专家和共享专家，并采用多层渐进式结构，
    解决了 MMoE 的负迁移和跷跷板现象。
    """
    
    def __init__(self, input_dim, num_layers, num_shared_experts, 
                 num_task_specific_experts, expert_hidden_dim,
                 task_hidden_dims, num_tasks, dropout=0.1):
        """
        初始化 PLE 模型
        
        Args:
            input_dim: 输入特征维度
            num_layers: PLE 层数，通常设置为 2-3 层
            num_shared_experts: 每层的共享专家数量
            num_task_specific_experts: 每层每个任务的任务特定专家数量
            expert_hidden_dim: 专家网络的输出维度
            task_hidden_dims: 任务塔隐藏层维度列表
            num_tasks: 任务数量
            dropout: Dropout 比率
        """
        super(PLE, self).__init__()
        self.num_layers = num_layers
        self.num_shared_experts = num_shared_experts
        self.num_task_specific_experts = num_task_specific_experts
        self.num_tasks = num_tasks
        
        # 构建多层 PLE 结构
        self.ple_layers = nn.ModuleList()
        prev_dim = input_dim  # 记录上一层的输出维度
        
        for layer_idx in range(num_layers):
            # 创建当前层的共享专家
            # 共享专家的输出可以被所有任务使用
            shared_experts = nn.ModuleList([
                Expert(prev_dim, expert_hidden_dim, dropout)
                for _ in range(num_shared_experts)
            ])
            
            # 创建当前层的任务特定专家
            # 每个任务有自己的专家组，这些专家只为特定任务服务
            task_specific_experts = nn.ModuleList()
            for _ in range(num_tasks):
                # 为当前任务创建 num_task_specific_experts 个专家
                task_experts = nn.ModuleList([
                    Expert(prev_dim, expert_hidden_dim, dropout)
                    for _ in range(num_task_specific_experts)
                ])
                task_specific_experts.append(task_experts)
            
            # 创建当前层的门控网络
            # 每个任务有独立的门控，决定如何组合共享专家和任务特定专家
            gates = nn.ModuleList()
            for task_idx in range(num_tasks):
                # 门控的输入包括：
                # 1. 原始输入特征（用于保持信息流）
                # 2. 上一层的输出（简化处理，这里用 prev_dim 表示）
                # 门控需要在(共享专家数 + 任务特定专家数)个专家中进行选择
                num_total_experts = num_shared_experts + num_task_specific_experts
                
                # 实际中，门控输入应该是前一层的所有专家输出
                # 这里简化为使用输入维度
                gate_input_dim = prev_dim
                gate = Gate(gate_input_dim, num_total_experts)
                gates.append(gate)
            
            # 将当前层的所有组件存储在 ModuleDict 中
            self.ple_layers.append(nn.ModuleDict({
                'shared_experts': shared_experts,
                'task_specific_experts': task_specific_experts,
                'gates': gates
            }))
            
            # 下一层的输入维度是专家的输出维度
            prev_dim = expert_hidden_dim
        
        # 构建任务塔（顶层预测网络）
        self.task_towers = nn.ModuleList()
        for _ in range(num_tasks):
            tower_layers = []
            prev_dim = expert_hidden_dim  # 任务塔的输入是最后一层 PLE 的输出
            for hidden_dim in task_hidden_dims:
                tower_layers.append(nn.Linear(prev_dim, hidden_dim))
                tower_layers.append(nn.ReLU())
                tower_layers.append(nn.Dropout(dropout))
                prev_dim = hidden_dim
            tower_layers.append(nn.Linear(prev_dim, 1))  # 最终输出
            self.task_towers.append(nn.Sequential(*tower_layers))
    
    def forward(self, x):
        """
        PLE 的前向传播
        
        流程：
        1. 逐层处理：每层都有共享专家和任务特定专家
        2. 在每层，每个任务通过门控组合专家输出
        3. 最后通过任务塔输出最终预测
        
        Args:
            x: 输入特征， shape 为[batch_size, input_dim]
        
        Returns:
            outputs: 各任务的输出， list of [batch_size, 1]
        """
        # 初始化：每个任务的输入都是原始特征 x
        task_outputs = [x] * self.num_tasks
        
        # 逐层处理 PLE 层
        for layer_idx, layer in enumerate(self.ple_layers):
            # 获取当前层的组件
            shared_experts = layer['shared_experts']
            task_specific_experts = layer['task_specific_experts']
            gates = layer['gates']
            
            # 第一步：计算共享专家的输出
            # 所有共享专家使用第一个任务的输出作为输入（简化处理）
            # 实际应用中可能需要更复杂的融合策略
            shared_outputs = []
            for expert in shared_experts:
                shared_outputs.append(expert(task_outputs[0]))
            # 堆叠共享专家输出：[batch_size, num_shared_experts, expert_hidden_dim]
            shared_outputs = torch.stack(shared_outputs, dim=1)
            
            # 第二步：为每个任务计算输出
            new_task_outputs = []
            for task_idx in range(self.num_tasks):
                # 2.1 计算当前任务的任务特定专家输出
                task_expert_outputs = []
                for expert in task_specific_experts[task_idx]:
                    # 使用当前任务的输出作为输入
                    task_expert_outputs.append(expert(task_outputs[task_idx]))
                # 堆叠：[batch_size, num_task_specific_experts, expert_hidden_dim]
                task_expert_outputs = torch.stack(task_expert_outputs, dim=1)
                
                # 2.2 合并共享专家和任务特定专家的输出
                # 拼接在专家维度上
                # shape: [batch_size, num_shared_experts + num_task_specific_experts, expert_hidden_dim]
                all_expert_outputs = torch.cat([shared_outputs, task_expert_outputs], dim=1)
                
                # 2.3 通过门控网络计算专家权重
                # 门控输入使用当前任务的输入（简化处理）
                # 实际可以使用更复杂的输入，如原始特征 + 专家输出的摘要
                gate_weights = gates[task_idx](task_outputs[task_idx])
                # gate_weights shape: [batch_size, num_shared_experts + num_task_specific_experts]
                
                # 2.4 加权组合所有专家输出
                # 扩展 gate_weights 的维度以便广播
                gate_weights = gate_weights.unsqueeze(-1)  # [batch_size, num_experts, 1]
                # 逐元素相乘后在专家维度求和
                task_output = (all_expert_outputs * gate_weights).sum(dim=1)
                # task_output shape: [batch_size, expert_hidden_dim]
                
                new_task_outputs.append(task_output)
            
            # 更新 task_outputs，作为下一层的输入
            task_outputs = new_task_outputs
        
        # 第三步：通过任务塔输出最终预测
        outputs = []
        for i, tower in enumerate(self.task_towers):
            output = tower(task_outputs[i])
            outputs.append(output)
        
        return outputs

# 使用示例
model = PLE(
    input_dim=1000,                    # 输入特征维度
    num_layers=2,                      # 2 层 PLE 结构
    num_shared_experts=2,              # 每层 2 个共享专家
    num_task_specific_experts=2,       # 每层每个任务 2 个特定专家
    expert_hidden_dim=256,             # 专家输出 256 维
    task_hidden_dims=[128, 64],        # 任务塔： 256 -> 128 -> 64 -> 1
    num_tasks=2,                       # 2 个任务
    dropout=0.1
)

x = torch.randn(32, 1000)
outputs = model(x)
print(f"Task 1 output shape: {outputs[0].shape}")  # torch.Size([32, 1])
print(f"Task 2 output shape: {outputs[1].shape}")  # torch.Size([32, 1])

PLE 的关键技术细节：

  1. 任务特定专家 vs 共享专家：

    • 任务特定专家只接收特定任务的梯度，学习任务特有的模式
    • 共享专家接收所有任务的梯度，学习任务间的公共知识
    • 门控网络决定两类专家的权重比例

  2. 渐进式提取的好处：

    • 底层：学习基础特征，任务间共享较多
    • 中层：学习中级特征，开始出现任务特定模式
    • 顶层：学习高级特征，任务独立性增强
    • 多层结构允许任务在不同抽象层次上有不同的共享程度

  3. 参数量分析：假设 2 个任务， 2 层 PLE，每层 2 个共享专家和 2 个任务特定专家，输入维度 1000，专家输出 256 。

    • 第 1 层： 2 个共享专家 + 2 × 2 个任务特定专家 = 6 个专家，参数量约 6 × 1000 × 256 ≈ 1.5M
    • 第 2 层：同样约 1.5M 参数（输入变为 256 维）
    • 总共约 3M 参数 + 门控参数 + 任务塔参数
    • 相比 MMoE（ 4 个专家）， PLE 参数量更大，但避免了负迁移

  4. 与 MMoE 的对比：

    • MMoE：所有专家共享，灵活性高但可能负迁移
    • PLE：分离任务特定和共享专家，牺牲部分参数效率换取更好的任务平衡

  5. 跷跷板现象的缓解：当任务 1 需要优化时，它可以更多地依赖任务特定专家，而不影响共享专家（任务 2 也在使用）。这样任务 1 的优化不会直接伤害任务 2 的性能。

  6. 工业实践建议：

    • 任务高度相关：可以减少任务特定专家，增加共享专家
    • 任务存在冲突：增加任务特定专家，减少共享专家
    • 层数选择： 2 层通常足够， 3 层在复杂场景下可能有提升
    • 调试技巧：可以打印门控权重，观察任务如何使用不同类型的专家

PLE 的优势

解决负迁移：通过任务特定专家，每个任务可以学习独立的特征表示，避免负迁移。

缓解跷跷板现象：渐进式分层结构允许任务在不同层次上进行不同程度的共享和独立。

更好的任务平衡：任务特定专家和共享专家的组合，让模型更好地平衡任务间的相关性和独立性。

PLE 的局限性

架构复杂度高：相比 MMoE， PLE 的架构更复杂，需要更多的超参数调优。

计算成本高：任务特定专家增加了参数量和计算量。

STEM-Net：解决负迁移问题

负迁移问题

负迁移（ Negative Transfer）是多任务学习中的核心问题：当任务之间存在冲突或相关性较低时，共享参数可能导致某些任务性能下降。

负迁移的原因： - 任务冲突：优化一个任务的方向与另一个任务相反 - 任务相关性低：任务之间没有足够的共同知识可以共享 - 数据分布差异：不同任务的数据分布差异很大

STEM-Net 架构

STEM-Net（ Selective Transfer and Extraction Network）通过选择性迁移机制解决负迁移问题。与 PLE 不同， STEM-Net 的核心创新在于显式学习任务间的相似度，并根据相似度动态调整共享程度。

核心设计思想： 1. 任务相似度学习：通过可学习的任务嵌入（ Task Embedding）和相似度网络，自动学习任务间的相似度矩阵。相似度高的任务可以更多地共享参数，相似度低的任务则减少共享。 2. 双重特征提取路径：每个任务同时拥有共享底层和任务特定底层两个特征提取路径。共享底层学习任务间的公共知识，任务特定底层学习任务特有的模式。 3. 选择性组合：根据任务相似度，动态决定如何组合共享特征和任务特定特征。相似度高的任务更依赖共享特征，相似度低的任务更依赖任务特定特征。

与 Shared-Bottom 和 PLE 的对比： - Shared-Bottom：所有任务强制共享所有底层参数，无法处理任务冲突 - PLE：通过任务特定专家和共享专家的分离缓解负迁移，但不显式建模任务相似度 - STEM-Net：显式学习任务相似度，根据相似度动态调整共享策略，更加灵活

下面我们实现 STEM-Net 模型。这个实现展示了如何通过任务嵌入和相似度网络来学习任务关系，以及如何通过双重特征提取路径来平衡共享和独立。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
class STEMNet(nn.Module):
    """
    STEM-Net: Selective Transfer and Extraction Network
    
    STEM-Net 通过显式学习任务相似度来解决负迁移问题。
    核心机制：
    1. 任务嵌入：将每个任务映射到一个低维向量空间
    2. 相似度网络：基于任务嵌入计算任务间的相似度
    3. 双重路径：共享底层 + 任务特定底层
    4. 选择性组合：根据相似度动态组合两种特征
    """
    
    def __init__(self, input_dim, shared_hidden_dims, task_hidden_dims, 
                 num_tasks, similarity_dim=64, dropout=0.1):
        """
        初始化 STEM-Net 模型
        
        Args:
            input_dim: 输入特征维度，例如 1000 维的用户和物品特征
            shared_hidden_dims: 共享层隐藏层维度列表，如[512, 256]
                               共享底层和任务特定底层都使用相同的维度结构
            task_hidden_dims: 任务塔隐藏层维度列表，如[128, 64]
                             任务塔的输入维度是共享维度× 2（共享特征+任务特定特征拼接）
            num_tasks: 任务数量，例如 2 表示 CTR 和 CVR 两个任务
            similarity_dim: 任务相似度表示维度，用于任务嵌入
                            较大的维度可以学习更复杂的任务关系，但会增加参数量
                            通常设置为 32-128 之间
            dropout: Dropout 比率，用于防止过拟合
        """
        super(STEMNet, self).__init__()
        self.num_tasks = num_tasks
        self.similarity_dim = similarity_dim
        
        # ========== 任务相似度学习模块 ==========
        # 任务嵌入：将每个任务 ID 映射到一个可学习的向量表示
        # 这个嵌入向量可以理解为任务的"身份特征"，用于学习任务间的关系
        # 例如， CTR 和 CVR 任务的嵌入可能比较接近（相似度高），
        # 而 CTR 和"停留时长"任务的嵌入可能距离较远（相似度低）
        self.task_embedding = nn.Embedding(num_tasks, similarity_dim)
        
        # 相似度网络：基于两个任务的嵌入向量，计算它们的相似度
        # 输入：两个任务嵌入的拼接 [task_i_emb, task_j_emb]，维度为 similarity_dim * 2
        # 输出：相似度分数，范围[0, 1]（通过 Sigmoid）
        # 相似度接近 1 表示任务高度相关，接近 0 表示任务冲突或独立
        self.similarity_network = nn.Sequential(
            nn.Linear(similarity_dim * 2, similarity_dim),  # 第一层：降维并融合两个任务嵌入
            nn.ReLU(),                                       # 激活函数
            nn.Linear(similarity_dim, 1),                   # 第二层：输出单个相似度分数
            nn.Sigmoid()                                     # 映射到[0, 1]区间
        )
        
        # ========== 共享底层网络 ==========
        # 共享底层学习所有任务的公共特征表示
        # 这个网络会被所有任务共享，学习任务间的共同知识
        shared_layers = []
        prev_dim = input_dim
        for hidden_dim in shared_hidden_dims:
            shared_layers.append(nn.Linear(prev_dim, hidden_dim))
            shared_layers.append(nn.ReLU())
            shared_layers.append(nn.Dropout(dropout))
            prev_dim = hidden_dim
        self.shared_bottom = nn.Sequential(*shared_layers)
        
        # ========== 任务特定底层网络 ==========
        # 为每个任务创建独立的底层网络，学习任务特有的特征表示
        # 这些网络只接收对应任务的梯度，不会被其他任务"污染"
        # 当任务冲突时，任务特定底层可以学习独立的模式，避免负迁移
        self.task_specific_bottoms = nn.ModuleList()
        for task_idx in range(num_tasks):
            task_layers = []
            prev_dim = input_dim
            for hidden_dim in shared_hidden_dims:
                task_layers.append(nn.Linear(prev_dim, hidden_dim))
                task_layers.append(nn.ReLU())
                task_layers.append(nn.Dropout(dropout))
                prev_dim = hidden_dim
            self.task_specific_bottoms.append(nn.Sequential(*task_layers))
        
        # ========== 任务塔 ==========
        # 任务塔的输入是共享特征和任务特定特征的拼接
        # 输入维度 = shared_hidden_dims[-1] * 2（共享特征维度 + 任务特定特征维度）
        self.task_towers = nn.ModuleList()
        for task_idx in range(num_tasks):
            tower_layers = []
            # 任务塔的输入维度是共享维度× 2（因为要拼接共享和任务特定特征）
            prev_dim = shared_hidden_dims[-1] * 2
            for hidden_dim in task_hidden_dims:
                tower_layers.append(nn.Linear(prev_dim, hidden_dim))
                tower_layers.append(nn.ReLU())
                tower_layers.append(nn.Dropout(dropout))
                prev_dim = hidden_dim
            # 最后一层输出单个预测值（ logit）
            tower_layers.append(nn.Linear(prev_dim, 1))
            self.task_towers.append(nn.Sequential(*tower_layers))
    
    def compute_task_similarity(self, task_i, task_j):
        """
        计算两个任务之间的相似度
        
        这个方法展示了如何基于任务嵌入计算相似度。
        在实际应用中，相似度可以用于：
        1. 动态调整共享程度（相似度高的任务更多共享）
        2. 分析任务关系（理解哪些任务相关，哪些冲突）
        3. 指导架构设计（相似度低的任务应该减少共享）
        
        Args:
            task_i: 任务 i 的 ID（标量或 tensor）
            task_j: 任务 j 的 ID（标量或 tensor）
        
        Returns:
            similarity: 任务相似度，范围[0, 1]， shape 取决于输入
        """
        # 获取任务嵌入向量
        # task_i_emb shape: [similarity_dim] 或 [batch_size, similarity_dim]
        task_i_emb = self.task_embedding(task_i)
        task_j_emb = self.task_embedding(task_j)
        
        # 拼接两个任务的嵌入向量
        # similarity_input shape: [similarity_dim * 2] 或 [batch_size, similarity_dim * 2]
        similarity_input = torch.cat([task_i_emb, task_j_emb], dim=-1)
        
        # 通过相似度网络计算相似度分数
        # similarity shape: [1] 或 [batch_size, 1]
        similarity = self.similarity_network(similarity_input)
        
        return similarity
    
    def forward(self, x, task_ids=None):
        """
        STEM-Net 的前向传播
        
        前向传播流程：
        1. 提取共享特征：所有任务共享的底层特征
        2. 提取任务特定特征：每个任务独立的底层特征
        3. 选择性组合：根据任务相似度（简化实现中直接拼接）组合两种特征
        4. 任务塔预测：基于组合特征进行任务特定的预测
        
        Args:
            x: 输入特征， shape 为[batch_size, input_dim]
            task_ids: 任务 ID， shape 为[batch_size]（可选，用于动态计算相似度）
                      在当前简化实现中未使用，但可以扩展为根据相似度动态调整组合权重
        
        Returns:
            outputs: 各任务的输出， list of [batch_size, 1]
                    每个任务返回一个预测值（ logit）
        """
        # 第一步：提取共享底层特征
        # shared_output shape: [batch_size, shared_hidden_dims[-1]]
        # 这个特征被所有任务共享，学习任务间的公共知识
        shared_output = self.shared_bottom(x)
        
        # 第二步：提取任务特定底层特征
        # 为每个任务计算独立的特征表示
        task_specific_outputs = []
        for task_bottom in self.task_specific_bottoms:
            # task_specific_output shape: [batch_size, shared_hidden_dims[-1]]
            task_specific_output = task_bottom(x)
            task_specific_outputs.append(task_specific_output)
        
        # 第三步：选择性组合共享特征和任务特定特征
        # 在当前简化实现中，我们直接拼接两种特征
        # 实际应用中，可以根据任务相似度动态调整组合权重：
        #   combined = similarity * shared_output + (1 - similarity) * task_specific_output
        outputs = []
        for task_idx in range(self.num_tasks):
            # 获取当前任务的任务特定特征
            task_specific_output = task_specific_outputs[task_idx]
            
            # 组合共享特征和任务特定特征
            # 拼接操作：在特征维度上拼接
            # combined_output shape: [batch_size, shared_hidden_dims[-1] * 2]
            # 前半部分是共享特征，后半部分是任务特定特征
            combined_output = torch.cat([shared_output, task_specific_output], dim=-1)
            
            # 第四步：通过任务塔输出最终预测
            # output shape: [batch_size, 1]
            output = self.task_towers[task_idx](combined_output)
            outputs.append(output)
        
        return outputs

STEM-Net 的关键技术细节：

  1. 任务相似度学习的意义：任务嵌入和相似度网络让模型能够自动发现任务间的关系。例如，如果 CTR 和 CVR 任务的嵌入向量在嵌入空间中距离很近，相似度网络会输出较高的相似度分数，表示这两个任务可以更多地共享参数。这种显式的相似度学习比隐式的共享机制（如 Shared-Bottom）更加灵活和可解释。

  2. 双重特征提取路径的设计：

    • 共享底层：学习所有任务的公共知识，参数量为 $ d h_1 h_2 ...（ d是输入维度， h_i$ 是隐藏层维度）
    • 任务特定底层：每个任务独立的底层，总参数量为 （ 是任务数量）
    • 总参数量：共享参数量 + 任务特定参数量，比完全独立的模型少，但比完全共享的模型多

  3. 选择性组合的扩展：当前实现中，我们简单地拼接共享特征和任务特定特征。更高级的实现可以根据任务相似度动态调整组合权重： 

    1
    2
    3
    4
    5
    6
    # 计算当前任务与其他所有任务的平均相似度
    similarities = [self.compute_task_similarity(task_idx, j) for j in range(self.num_tasks)]
    avg_similarity = torch.mean(torch.stack(similarities))

    # 根据相似度加权组合
    combined_output = avg_similarity * shared_output + (1 - avg_similarity) * task_specific_output
    这样，相似度高的任务会更依赖共享特征，相似度低的任务会更依赖任务特定特征。

  4. 与 PLE 的对比：

    • PLE：通过任务特定专家和共享专家的分离来缓解负迁移，但不显式学习任务相似度
    • STEM-Net：显式学习任务相似度，并根据相似度动态调整共享策略
    • 适用场景： STEM-Net 更适合任务关系复杂、需要精细控制共享程度的场景

  5. 参数量分析：假设输入维度 1000，共享层[512, 256]， 2 个任务，相似度维度 64 。

    • 任务嵌入： 参数
    • 相似度网络： 参数
    • 共享底层： 参数
    • 任务特定底层： 参数
    • 任务塔： 参数
    • 总参数量约 2.1M，比两个完全独立的模型（约 2.8M）少约 25%

  6. 训练技巧：

    • 任务嵌入的初始化：可以使用预训练的任务嵌入，或者根据任务标签的相似度初始化
    • 相似度正则化：可以添加正则化项，鼓励相似度高的任务嵌入接近，相似度低的任务嵌入远离
    • 动态相似度更新：在训练过程中，任务相似度会随着模型学习而更新，反映任务间的实际关系

任务关系建模

任务相似度度量

在多任务学习中，理解任务间的关系至关重要。常见的任务相似度度量方法：

相关性分析： - 皮尔逊相关系数：衡量任务标签之间的线性相关性 - 互信息：衡量任务标签之间的非线性相关性

梯度相似度： - 计算不同任务在共享参数上的梯度相似度 - 梯度方向相似表示任务相关，相反表示任务冲突

特征相似度： - 计算不同任务学习到的特征表示的相似度 - 使用余弦相似度、欧氏距离等度量

动态任务关系学习

在多任务学习中，任务间的关系不是静态的，而是会随着训练过程动态变化。例如，在训练初期， CTR 和 CVR 任务可能都关注基础的用户特征，关系较密切；但随着训练的深入， CVR 任务可能开始关注更细粒度的转化相关特征，与 CTR 的关系可能发生变化。

动态任务关系学习通过可学习的任务嵌入和关系预测网络，让模型自动发现和更新任务间的关系。这种方法比固定的人工设计关系更加灵活，能够适应不同训练阶段的任务关系变化。

下面我们实现一个通用的任务关系建模模块。这个模块可以学习任务间的三种基本关系：相关（可以共享参数）、冲突（应该独立学习）、独立（互不影响）。在实际应用中，可以根据学习到的关系动态调整多任务架构的共享策略。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
class TaskRelationshipModel(nn.Module):
    """
    任务关系建模模块
    
    这个模块通过学习任务嵌入和关系预测网络，自动发现任务间的关系。
    关系类型：
    1. 相关（ Positive）：任务可以共享参数，相互促进
    2. 冲突（ Negative）：任务存在冲突，应该减少共享
    3. 独立（ Neutral）：任务互不影响，可以独立学习
    
    应用场景：
    - 指导多任务架构设计（哪些任务应该共享，哪些应该独立）
    - 动态调整损失权重（相关任务可以共享权重，冲突任务需要平衡）
    - 分析任务关系（理解为什么某些任务组合效果好，某些效果差）
    """
    
    def __init__(self, num_tasks, embedding_dim=64):
        """
        初始化任务关系建模模块
        
        Args:
            num_tasks: 任务数量，例如 2 表示 CTR 和 CVR 两个任务
            embedding_dim: 任务嵌入维度，用于表示任务的"身份特征"
                           - 较大的维度可以学习更复杂的任务关系
                           - 但会增加参数量和计算成本
                           - 通常设置为 32-128 之间
        """
        super(TaskRelationshipModel, self).__init__()
        self.num_tasks = num_tasks
        self.embedding_dim = embedding_dim
        
        # 任务嵌入：将每个任务 ID 映射到一个可学习的向量表示
        # 这个嵌入向量可以理解为任务的"身份特征"
        # 在嵌入空间中，相似的任务（如 CTR 和 CVR）应该距离较近，
        # 冲突的任务（如 CTR 和停留时长）应该距离较远
        # shape: [num_tasks, embedding_dim]
        self.task_embeddings = nn.Embedding(num_tasks, embedding_dim)
        
        # 关系预测网络：基于两个任务的嵌入向量，预测它们的关系类型
        # 输入：两个任务嵌入的拼接 [task_i_emb, task_j_emb]，维度为 embedding_dim * 2
        # 输出： 3 个 logits，分别对应"相关"、"冲突"、"独立"三种关系
        # 可以通过 Softmax 得到关系类型的概率分布
        self.relationship_network = nn.Sequential(
            nn.Linear(embedding_dim * 2, embedding_dim),  # 第一层：降维并融合两个任务嵌入
            nn.ReLU(),                                     # 激活函数，引入非线性
            nn.Linear(embedding_dim, 3)                   # 第二层：输出 3 种关系的 logits
            # 注意：这里不添加 Softmax，因为通常使用 CrossEntropyLoss 时会自动应用
        )
    
    def forward(self, task_i, task_j):
        """
        预测任务 i 和任务 j 的关系
        
        这个方法展示了如何基于任务嵌入预测任务关系。
        在实际应用中，预测的关系可以用于：
        1. 动态调整多任务架构的共享策略
        2. 指导损失权重的设置
        3. 分析任务间的相互作用
        
        Args:
            task_i: 任务 i 的 ID，可以是标量（单个任务）或 tensor（批量任务）
                    例如： torch.tensor(0) 表示 CTR 任务
            task_j: 任务 j 的 ID，格式同 task_i
                    例如： torch.tensor(1) 表示 CVR 任务
        
        Returns:
            relationship_logits: 关系类型的 logits， shape 为[3]或[batch_size, 3]
                                 - relationship_logits[0]: "相关"关系的 logit
                                 - relationship_logits[1]: "冲突"关系的 logit
                                 - relationship_logits[2]: "独立"关系的 logit
                                 可以通过 Softmax 得到概率分布
        """
        # 第一步：获取任务嵌入向量
        # task_i_emb shape: [embedding_dim] 或 [batch_size, embedding_dim]
        # 如果 task_i 是标量，则输出是 1 维；如果是 tensor，则输出是 2 维
        task_i_emb = self.task_embeddings(task_i)
        task_j_emb = self.task_embeddings(task_j)
        
        # 第二步：拼接两个任务的嵌入向量
        # 拼接操作在最后一个维度上进行
        # relationship_input shape: [embedding_dim * 2] 或 [batch_size, embedding_dim * 2]
        # 前半部分是任务 i 的嵌入，后半部分是任务 j 的嵌入
        relationship_input = torch.cat([task_i_emb, task_j_emb], dim=-1)
        
        # 第三步：通过关系预测网络得到关系类型的 logits
        # relationship_logits shape: [3] 或 [batch_size, 3]
        # 三个值分别对应"相关"、"冲突"、"独立"三种关系
        relationship_logits = self.relationship_network(relationship_input)
        
        return relationship_logits
    
    def get_task_similarity_matrix(self):
        """
        计算所有任务对的相似度矩阵
        
        这个方法返回一个对称矩阵，表示所有任务对之间的相似度。
        可以用于可视化任务关系，或者指导多任务架构的设计。
        
        Returns:
            similarity_matrix: 任务相似度矩阵， shape 为[num_tasks, num_tasks]
                              similarity_matrix[i][j] 表示任务 i 和任务 j 的相似度
        """
        similarity_matrix = torch.zeros(self.num_tasks, self.num_tasks)
        
        with torch.no_grad():
            for i in range(self.num_tasks):
                for j in range(self.num_tasks):
                    # 获取关系预测的 logits
                    logits = self.forward(torch.tensor(i), torch.tensor(j))
                    # 使用"相关"关系的概率作为相似度（也可以使用其他定义）
                    probs = torch.softmax(logits, dim=-1)
                    similarity_matrix[i][j] = probs[0].item()  # probs[0]是"相关"的概率
        
        return similarity_matrix

任务关系建模的关键技术细节：

  1. 任务嵌入的学习：任务嵌入是可学习的参数，在训练过程中会不断更新。如果两个任务在训练过程中经常产生相似的梯度（表示它们关注相似的特征），它们的嵌入向量会在嵌入空间中逐渐靠近；反之，如果两个任务的梯度方向相反（表示它们存在冲突），它们的嵌入向量会逐渐远离。

  2. 关系类型的定义：

    • 相关（ Positive）：任务可以共享参数，相互促进。例如， CTR 和 CVR 任务都关注用户对商品的兴趣，可以共享底层特征。
    • 冲突（ Negative）：任务存在冲突，应该减少共享。例如， CTR 和"停留时长"可能存在冲突：高 CTR 可能带来低停留时长（用户快速点击但快速离开）。
    • 独立（ Neutral）：任务互不影响，可以独立学习。例如， CTR 和"分享"任务可能相对独立。

  3. 关系预测的应用：

    • 架构设计：如果预测两个任务"相关"，可以让它们共享更多参数；如果预测"冲突"，应该减少共享或使用任务特定参数。
    • 损失权重：相关任务的损失权重可以设置为相似的值，冲突任务的权重需要仔细平衡。
    • 任务分析：通过可视化任务相似度矩阵，可以理解任务间的关系，指导多任务学习的设计。

  4. 训练策略：

    • 联合训练：任务关系模型可以与多任务模型联合训练，让关系预测和任务学习相互促进。
    • 预训练：也可以先单独训练任务关系模型，然后用学习到的关系指导多任务模型的训练。
    • 动态更新：在训练过程中，任务关系会动态更新，反映任务间的实际关系变化。

  5. 扩展方向：

    • 层次化关系：可以学习更细粒度的任务关系，如"高度相关"、"中度相关"、"轻度相关"等。
    • 上下文相关的关系：任务关系可能依赖于输入特征，可以学习上下文相关的任务关系。
    • 多关系类型：除了"相关/冲突/独立"，还可以学习其他关系类型，如"顺序关系"（ CTR → CVR）、"竞争关系"等。

Loss 平衡策略

问题：不同任务的损失尺度差异

在多任务学习中，不同任务的损失尺度可能差异很大： - CTR 损失通常在 0.1-0.5 之间 - CVR 损失通常在 0.01-0.1 之间 - 回归任务的 MSE 损失可能在 1-100 之间

如果直接相加，损失尺度大的任务会 dominate 训练过程。

常见平衡策略

固定权重： $$

L = _{i=1}^T w_i L_i$$

需要人工调参，难以找到最优权重。

不确定性加权（ Uncertainty Weighting）： $$

L = _{i=1}^T L_i + _i$$

其中 是可学习的任务不确定性参数。

GradNorm： 动态调整任务权重，使得不同任务的梯度范数相似。

动态权重调整（ Dynamic Weight Adjustment）： 根据任务性能动态调整权重。

代码实现

在多任务学习中，不同任务的损失尺度可能差异巨大。例如， CTR 损失可能在 0.3 左右， CVR 损失可能在 0.03 左右，而回归任务的 MSE 损失可能在 100 以上。如果直接将这些损失相加，损失大的任务会主导训练过程，导致其他任务优化不充分。

下面我们实现两种常用的自动损失平衡策略：不确定性加权（ Uncertainty Weighting）和 GradNorm。这两种方法都能自动学习任务权重，无需人工调参。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
class UncertaintyWeighting(nn.Module):
    """
    不确定性加权损失平衡（ Multi-Task Learning Using Uncertainty to Weigh Losses）
    
    核心思想：为每个任务学习一个不确定性参数σ_i，用它来自动调整任务权重。
    损失函数： L = Σ[1/(2 σ_i ²) * L_i + log(σ_i)]
    
    - 第一项：损失被不确定性归一化，不确定性大的任务权重小
    - 第二项： log(σ_i)是正则化项，防止σ_i 无限增大
    
    这种方法在论文"Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics"中提出。
    """
    
    def __init__(self, num_tasks):
        """
        Args:
            num_tasks: 任务数量
        """
        super(UncertaintyWeighting, self).__init__()
        self.num_tasks = num_tasks
        
        # 可学习的任务不确定性参数（实际存储的是 log(σ)，便于优化）
        # 初始化为 0，对应σ=1（所有任务初始权重相同）
        # 使用 log(σ)而不是σ有两个好处：
        # 1. 确保σ始终为正（因为σ = exp(log_σ)）
        # 2. 优化更稳定（ log 空间的梯度更平滑）
        self.log_sigma = nn.Parameter(torch.zeros(num_tasks))
    
    def forward(self, losses):
        """
        计算加权后的总损失
        
        数学原理：
        假设任务 i 的噪声服从高斯分布，方差为σ_i ²，则负对数似然为：
        -log p(y_i|f_i) = 1/(2 σ_i ²) * L_i + log(σ_i) + const
        
        Args:
            losses: 各任务的损失， list of scalar tensors
                   例如：[ctr_loss, cvr_loss]
        
        Returns:
            weighted_loss: 加权后的总损失（标量）
        """
        weighted_losses = []
        
        for i, loss in enumerate(losses):
            # 计算当前任务的加权损失
            # σ = exp(log_σ)，因此σ² = exp(2*log_σ)
            # 1/(2 σ²) = 1/(2*exp(2*log_σ)) = exp(-2*log_σ)/2
            
            # 第一项：损失的归一化项 L_i / (2 σ_i ²)
            precision = torch.exp(-2 * self.log_sigma[i])  # 1/σ²，称为精度
            weighted_loss_term = 0.5 * precision * loss
            
            # 第二项：正则化项 log(σ_i)
            # 防止模型通过增大σ来减小总损失（相当于忽略该任务）
            regularization_term = self.log_sigma[i]
            
            # 总权重损失
            weighted_loss = weighted_loss_term + regularization_term
            weighted_losses.append(weighted_loss)
        
        # 所有任务的加权损失求和
        total_loss = sum(weighted_losses)
        
        return total_loss

class GradNorm(nn.Module):
    """
    GradNorm：动态调整任务权重，使得不同任务的梯度范数相似
    
    核心思想：
    1. 任务权重是可学习参数
    2. 计算每个任务对共享参数的梯度范数
    3. 让梯度范数与任务的相对训练速度成正比
    4. 通过梯度范数损失调整任务权重
    
    目标：优化快的任务（损失下降快）应该有更大的梯度，优化慢的任务应该有更小的梯度。
    这样可以平衡不同任务的优化速度。
    """
    
    def __init__(self, num_tasks, alpha=0.12):
        """
        Args:
            num_tasks: 任务数量
            alpha: 梯度范数平衡系数，控制权重调整的激进程度
                  - α=0: 所有任务梯度范数相等（完全平衡）
                  - α>0: 优化快的任务梯度范数更大（按相对速度加权）
                  - 通常设置为 0.12（经验值）
        """
        super(GradNorm, self).__init__()
        self.num_tasks = num_tasks
        self.alpha = alpha
        
        # 可学习的任务权重
        # 初始化为 1，表示所有任务初始权重相同
        self.task_weights = nn.Parameter(torch.ones(num_tasks))
        
        # 记录初始损失（用于计算相对损失）
        # 在第一次 forward 时设置
        self.initial_losses = None
    
    def compute_grad_norm(self, model, losses):
        """
        计算各任务在共享参数上的梯度范数
        
        梯度范数反映了当前任务的损失对模型参数的影响程度。
        梯度范数大：该任务对参数更新的"拉力"大
        梯度范数小：该任务对参数更新的"拉力"小
        
        Args:
            model: 多任务模型（需要有共享参数）
            losses: 各任务的损失， list of scalar tensors
        
        Returns:
            grad_norms: 各任务的梯度范数， shape 为[num_tasks]
        """
        grad_norms = []
        
        for i, loss in enumerate(losses):
            # 计算加权损失（使用当前任务权重）
            weighted_loss = self.task_weights[i] * loss
            
            # 计算梯度（对共享参数求导）
            # retain_graph=True: 保留计算图，因为还要计算其他任务的梯度
            # create_graph=True: 创建梯度的计算图，用于后续的梯度范数损失优化
            grad = torch.autograd.grad(
                weighted_loss, 
                model.parameters(),
                retain_graph=True,   # 保留图以计算其他任务
                create_graph=True    # 创建图以优化梯度范数损失
            )
            
            # 计算梯度的 L2 范数
            # 将所有参数的梯度展平并拼接，然后计算范数
            grad_norm = torch.norm(torch.cat([g.flatten() for g in grad]))
            grad_norms.append(grad_norm)
        
        return torch.stack(grad_norms)
    
    def forward(self, model, losses):
        """
        GradNorm 的前向传播
        
        Args:
            model: 多任务模型
            losses: 各任务的损失， list of scalar tensors
        
        Returns:
            total_loss: 加权后的总任务损失
            grad_norm_loss: GradNorm 正则化损失（用于更新任务权重）
        """
        # 第一步：记录初始损失（只在第一次调用时执行）
        if self.initial_losses is None:
            # 使用 detach()避免计算图保留，只记录数值
            self.initial_losses = torch.stack([l.detach() for l in losses])
        
        # 第二步：计算加权总损失（用于更新模型参数）
        weighted_losses = [self.task_weights[i] * losses[i] for i in range(self.num_tasks)]
        total_loss = sum(weighted_losses)
        
        # 第三步：计算各任务的梯度范数
        grad_norms = self.compute_grad_norm(model, losses)
        avg_grad_norm = grad_norms.mean()  # 平均梯度范数
        
        # 第四步：计算相对损失（训练速度的指标）
        # relative_loss = L_i(t) / L_i(0)
        # 损失下降快的任务， relative_loss 小；损失下降慢的任务， relative_loss 大
        losses_tensor = torch.stack(losses)
        relative_losses = losses_tensor / (self.initial_losses + 1e-8)  # 加小常数防止除零
        relative_losses = relative_losses.detach()  # 不计算梯度
        
        # 第五步：计算目标梯度范数
        # target_grad_norm_i = avg_grad_norm * (relative_loss_i)^α
        # α=0: 所有任务目标梯度范数相等
        # α>0: 损失下降慢的任务（ relative_loss 大）目标梯度范数更大
        target_grad_norms = avg_grad_norm * (relative_losses ** self.alpha)
        
        # 第六步：计算 GradNorm 正则化损失
        # 让实际梯度范数接近目标梯度范数
        # 这个损失用于更新任务权重（不更新模型参数）
        grad_norm_loss = torch.abs(grad_norms - target_grad_norms).sum()
        
        return total_loss, grad_norm_loss

损失平衡策略的使用方法：

  1. 不确定性加权的训练流程： 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    # 创建模型和损失平衡器
    model = MMoE(...)
    loss_balancer = UncertaintyWeighting(num_tasks=2)

    # 训练循环
    optimizer = torch.optim.Adam(
        list(model.parameters()) + list(loss_balancer.parameters()),
        lr=0.001
    )

    for batch in dataloader:
        # 前向传播
        outputs = model(features)
        task_losses = [criterion(outputs[i], labels[i]) for i in range(2)]
        
        # 损失平衡
        total_loss = loss_balancer(task_losses)
        
        # 反向传播
        optimizer.zero_grad()
        total_loss.backward()
        optimizer.step()
        
        # 可以打印学习到的不确定性参数
        print(f"Sigma: {torch.exp(loss_balancer.log_sigma).detach()}")

  2. GradNorm 的训练流程： 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    # 创建模型和损失平衡器
    model = MMoE(...)
    loss_balancer = GradNorm(num_tasks=2, alpha=0.12)

    # 分离优化器：模型参数和任务权重分开优化
    model_optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
    weight_optimizer = torch.optim.Adam([loss_balancer.task_weights], lr=0.025)

    for batch in dataloader:
        # 前向传播
        outputs = model(features)
        task_losses = [criterion(outputs[i], labels[i]) for i in range(2)]
        
        # 计算总损失和梯度范数损失
        total_loss, grad_norm_loss = loss_balancer(model, task_losses)
        
        # 更新模型参数
        model_optimizer.zero_grad()
        total_loss.backward(retain_graph=True)  # 保留图以更新权重
        model_optimizer.step()
        
        # 更新任务权重
        weight_optimizer.zero_grad()
        grad_norm_loss.backward()
        weight_optimizer.step()
        
        # 归一化任务权重（可选，保持权重和不变）
        with torch.no_grad():
            loss_balancer.task_weights.div_(loss_balancer.task_weights.sum() / 2)

两种方法的对比：

特性 不确定性加权 GradNorm
原理 基于任务不确定性的贝叶斯解释 基于梯度范数的动态平衡
参数 每个任务 1 个不确定性参数 每个任务 1 个权重参数 + α
计算成本 低（只需要计算损失） 高（需要计算梯度范数）
优化难度 容易（与模型参数一起优化） 中等（需要分离优化器）
适用场景 通用，适合大多数场景 任务差异大、需要精细平衡的场景
缺点 可能陷入局部最优（某些任务被忽略） 计算开销大，需要仔细调参

实践建议： - 优先尝试不确定性加权，实现简单效果好 - 任务差异极大时考虑 GradNorm - 可以结合人工权重：先用固定权重训练几轮，再启用自动平衡 - 监控各任务的权重变化，防止某些任务权重趋近于 0

工业实践案例

阿里巴巴 ESMM 实践

业务场景：淘宝商品推荐，需要同时预估 CTR 和 CVR 。

模型架构： ESMM 模型，共享底层特征提取， CTR 和 CVR 独立塔。

效果提升： - CVR 预估 AUC 提升 2.18% - 通过 CTCVR 间接计算 CVR，解决了样本选择偏差问题

关键经验： - CTR 和 CVR 共享底层特征，充分利用 CTR 的丰富样本 - CTCVR 损失在所有曝光样本上计算，避免了样本选择偏差 - 通过 CTR 和 CTCVR 的除法得到 CVR，保证了概率的一致性

腾讯 PLE 实践

业务场景：腾讯视频推荐，需要同时优化 CTR 、播放时长、完播率等多个目标。

模型架构： PLE 模型， 2 层渐进式提取，每层包含共享专家和任务特定专家。

效果提升： - 相比 MMoE， AUC 提升 0.39% - 解决了 MMoE 的负迁移和跷跷板现象

关键经验： - 任务特定专家解决了负迁移问题 - 渐进式分层结构允许任务在不同层次上进行不同程度的共享 - 门控网络自动学习任务间的共享和独立关系

Google MMoE 实践

业务场景： YouTube 视频推荐，需要同时优化点击、观看时长、互动等多个目标。

模型架构： MMoE 模型， 4 个专家网络，每个任务独立的门控网络。

效果提升： - 多个离线指标均有提升 - 相比单任务模型，参数量减少但性能提升

关键经验： - 专家数量需要根据任务复杂度调整 - 门控网络可以自动学习任务关系，无需人工设计 - 多任务学习提升了模型的泛化能力

完整代码实现

在实际应用中，多任务学习不仅需要模型架构，还需要完整的数据处理、训练流程、评估指标等配套代码。本节提供一套完整的实现，包括数据准备、训练流程、评估指标、样本平衡策略等，帮助读者快速上手多任务学习的实践。

数据准备

多任务学习的数据准备与单任务学习的主要区别在于：每个样本需要同时包含多个任务的标签。例如，一个曝光样本需要同时有 CTR 标签（是否点击）和 CVR 标签（是否转化）。这要求我们在数据收集和预处理阶段就要考虑多任务的需求。

下面我们实现一个通用的多任务数据集类，它可以处理任意数量的任务，并支持灵活的数据格式。同时，我们还提供了一个合成数据生成函数，用于快速测试多任务模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
import numpy as np
import pandas as pd
from torch.utils.data import Dataset, DataLoader

class MultiTaskDataset(Dataset):
    """
    多任务学习数据集
    
    这个数据集类支持同时加载多个任务的标签，每个样本包含：
    - 输入特征：所有任务共享的特征向量
    - 多个任务标签：每个任务一个标签
    
    设计要点：
    1. 支持不同任务的不同标签格式（二分类、多分类、回归等）
    2. 支持任务标签的缺失（某些样本可能没有某些任务的标签）
    3. 支持灵活的数据加载和批处理
    """
    
    def __init__(self, features, labels_dict):
        """
        初始化多任务数据集
        
        Args:
            features: 特征矩阵， shape 为[n_samples, n_features]
                      - n_samples: 样本数量
                      - n_features: 特征维度
                      - 可以是 numpy 数组或 torch tensor
            labels_dict: 标签字典，格式为 {task_name: labels}
                         - task_name: 任务名称，如'ctr'、'cvr'
                         - labels: 该任务的标签， shape 为[n_samples]或[n_samples, label_dim]
                         - 对于二分类任务， labels 通常是 0/1
                         - 对于回归任务， labels 是连续值
                         - 对于缺失标签，可以使用-1 或 NaN 表示
        """
        self.features = features
        self.labels_dict = labels_dict
        self.task_names = list(labels_dict.keys())
        
        # 验证数据一致性：确保所有任务的标签数量与特征数量一致
        n_samples = len(features)
        for task_name, labels in labels_dict.items():
            assert len(labels) == n_samples, \
                f"Task {task_name} has {len(labels)} labels, but features have {n_samples} samples"
    
    def __len__(self):
        """返回数据集大小"""
        return len(self.features)
    
    def __getitem__(self, idx):
        """
        获取单个样本
        
        返回格式：
        {
            'features': 特征向量,
            'task1': 任务 1 的标签,
            'task2': 任务 2 的标签,
            ...
        }
        
        Args:
            idx: 样本索引
        
        Returns:
            sample: 包含特征和所有任务标签的字典
        """
        sample = {
            'features': self.features[idx],  # 输入特征
            # 将所有任务的标签添加到样本中
            **{task: self.labels_dict[task][idx] for task in self.task_names}
        }
        return sample

# 生成示例数据
def generate_synthetic_data(n_samples=10000, n_features=100, num_tasks=2):
    """
    生成合成多任务数据
    
    这个函数用于快速生成测试数据，模拟真实推荐系统中的多任务场景。
    生成的数据包括：
    - CTR 任务：模拟点击率预测，使用前 50 个特征
    - CVR 任务：模拟转化率预测，使用后 50 个特征，且只在点击样本上有标签
    
    在实际应用中，应该使用真实的数据集，如：
    - MovieLens 数据集（评分、点击等多任务）
    - 电商数据集（ CTR 、 CVR 、 GMV 等多任务）
    - 新闻推荐数据集（点击、阅读时长、分享等多任务）
    
    Args:
        n_samples: 样本数量，默认 10000
        n_features: 特征维度，默认 100
        num_tasks: 任务数量，默认 2（ CTR 和 CVR）
    
    Returns:
        features: 特征矩阵， shape 为[n_samples, n_features]
        labels_dict: 标签字典，{task_name: labels}
    """
    # 生成随机特征
    # 实际应用中，特征应该来自特征工程，包括：
    # - 用户特征：年龄、性别、历史行为等
    # - 物品特征：类别、价格、描述等
    # - 上下文特征：时间、位置、设备等
    # - 交互特征：用户-物品的交叉特征
    features = np.random.randn(n_samples, n_features)
    
    # ========== 任务 1： CTR（点击率） ==========
    # CTR 任务模拟：用户是否会点击推荐物品
    # 使用前 50 个特征生成 CTR 的 logit
    # 实际应用中， CTR 标签来自用户的实际点击行为
    ctr_weights = np.random.randn(50)  # 模拟特征权重
    ctr_logits = np.dot(features[:, :50], ctr_weights) + np.random.randn(n_samples) * 0.1
    # 通过 sigmoid 函数将 logit 转换为概率，然后采样得到二分类标签
    ctr_probs = 1 / (1 + np.exp(-ctr_logits))
    ctr_labels = (ctr_probs > np.random.rand(n_samples)).astype(float)
    
    # ========== 任务 2： CVR（转化率） ==========
    # CVR 任务模拟：用户点击后是否会转化（购买、下载等）
    # 关键点： CVR 标签只在点击样本上存在（只有点击的用户才可能转化）
    # 这是 ESMM 要解决的样本选择偏差问题的核心
    cvr_weights = np.random.randn(50)  # 使用后 50 个特征（与 CTR 不同，模拟任务差异）
    cvr_logits = np.dot(features[:, 50:], cvr_weights) + np.random.randn(n_samples) * 0.1
    cvr_probs = 1 / (1 + np.exp(-cvr_logits))
    
    # 初始化 CVR 标签为全 0（表示未点击或未转化）
    cvr_labels = np.zeros(n_samples)
    # 只在点击样本上生成 CVR 标签
    clicked_indices = np.where(ctr_labels == 1)[0]
    if len(clicked_indices) > 0:
        cvr_labels[clicked_indices] = (
            cvr_probs[clicked_indices] > np.random.rand(len(clicked_indices))
        ).astype(float)
    
    # 构建标签字典
    labels_dict = {
        'ctr': ctr_labels,  # CTR 标签：所有样本都有
        'cvr': cvr_labels   # CVR 标签：只有点击样本有（非点击样本为 0）
    }
    
    return features, labels_dict

# 使用示例
# 生成合成数据
features, labels_dict = generate_synthetic_data(n_samples=10000, n_features=100, num_tasks=2)

# 创建数据集
dataset = MultiTaskDataset(features, labels_dict)

# 创建数据加载器
# batch_size: 批次大小，影响训练速度和内存使用
# shuffle: 是否打乱数据，训练时通常设为 True
dataloader = DataLoader(dataset, batch_size=32, shuffle=True)

# 查看数据格式
print(f"Dataset size: {len(dataset)}")
print(f"Task names: {dataset.task_names}")
print(f"Feature shape: {features.shape}")
print(f"CTR positive ratio: {labels_dict['ctr'].mean():.2%}")
print(f"CVR positive ratio (among clicks): {labels_dict['cvr'][labels_dict['ctr']==1].mean():.2%}")

训练流程

多任务学习的训练流程与单任务学习类似，但有几个关键区别：

  1. 多任务损失计算：需要为每个任务单独计算损失，然后通过损失平衡策略组合
  2. 损失平衡：不同任务的损失尺度可能差异很大，需要使用不确定性加权或 GradNorm 等方法平衡
  3. 梯度处理：共享参数的梯度来自多个任务，需要确保梯度正确聚合
  4. 评估指标：需要同时评估所有任务的性能，不能只看单一指标

下面我们实现一个完整的训练函数，它支持多种损失平衡策略，并提供了详细的训练日志。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
import torch.optim as optim
from torch.nn import BCEWithLogitsLoss

def train_multi_task_model(model, dataloader, num_epochs=10, lr=0.001, 
                          loss_balancer=None, device='cuda'):
    """
    训练多任务模型
    
    这个训练函数实现了多任务学习的完整训练流程，包括：
    1. 前向传播：同时预测多个任务
    2. 损失计算：为每个任务单独计算损失
    3. 损失平衡：使用不确定性加权或 GradNorm 等方法平衡多任务损失
    4. 反向传播：更新模型参数
    5. 训练监控：记录训练过程中的损失和指标
    
    Args:
        model: 多任务模型（如 MMoE 、 PLE 等），需要有以下属性：
               - num_tasks: 任务数量
               - task_names: 任务名称列表（可选）
        dataloader: 数据加载器，每个 batch 包含 features 和所有任务的标签
        num_epochs: 训练轮数，通常设置为 10-100
        lr: 学习率，通常设置为 0.001-0.01
        loss_balancer: 损失平衡器，可以是 UncertaintyWeighting 或 GradNorm
                      如果为 None，则使用默认的 UncertaintyWeighting
        device: 训练设备，'cuda'或'cpu'
    
    Returns:
        model: 训练好的模型
    """
    # 将模型移到指定设备
    model = model.to(device)
    
    # 创建优化器
    # 如果使用 GradNorm，需要将损失平衡器的参数也加入优化器
    if isinstance(loss_balancer, GradNorm):
        # GradNorm 需要分离优化器，这里简化处理
        optimizer = optim.Adam(model.parameters(), lr=lr)
    else:
        # 不确定性加权等方法的参数可以与模型参数一起优化
        if loss_balancer is not None:
            optimizer = optim.Adam(
                list(model.parameters()) + list(loss_balancer.parameters()),
                lr=lr
            )
        else:
            optimizer = optim.Adam(model.parameters(), lr=lr)
    
    # 损失函数：每个任务使用相同的损失函数
    # BCEWithLogitsLoss = Sigmoid + BCE，适用于二分类任务
    # 对于回归任务，可以使用 MSELoss
    # 对于多分类任务，可以使用 CrossEntropyLoss
    criterion = BCEWithLogitsLoss()
    
    # 损失平衡器：如果没有提供，使用默认的不确定性加权
    if loss_balancer is None:
        loss_balancer = UncertaintyWeighting(model.num_tasks)
        loss_balancer = loss_balancer.to(device)
        # 将损失平衡器的参数加入优化器
        optimizer = optim.Adam(
            list(model.parameters()) + list(loss_balancer.parameters()),
            lr=lr
        )
    else:
        loss_balancer = loss_balancer.to(device)
    
    # 训练循环
    for epoch in range(num_epochs):
        model.train()  # 设置为训练模式（启用 Dropout 等）
        epoch_total_loss = 0
        epoch_task_losses = [0.0] * model.num_tasks  # 记录每个任务的损失
        
        # 遍历所有 batch
        for batch_idx, batch in enumerate(dataloader):
            # ========== 数据准备 ==========
            # 提取特征和标签
            features = batch['features'].float().to(device)
            # 获取所有任务的标签
            # 假设模型有 task_names 属性，否则使用默认顺序
            if hasattr(model, 'task_names'):
                task_labels = [batch[task].float().to(device) for task in model.task_names]
            else:
                # 如果没有 task_names，假设标签按顺序存储在 batch 中
                task_labels = [batch[f'task_{i}'].float().to(device) 
                              for i in range(model.num_tasks)]
            
            # ========== 前向传播 ==========
            # 模型同时预测所有任务
            # outputs 是一个列表，每个元素对应一个任务的预测结果
            outputs = model(features)
            
            # ========== 损失计算 ==========
            # 为每个任务单独计算损失
            task_losses = []
            for i, (output, label) in enumerate(zip(outputs, task_labels)):
                # output shape: [batch_size, 1]
                # label shape: [batch_size]
                # squeeze()移除维度 1，使形状匹配
                loss = criterion(output.squeeze(), label)
                task_losses.append(loss)
                epoch_task_losses[i] += loss.item()
            
            # ========== 损失平衡 ==========
            # 使用损失平衡策略组合多任务损失
            if isinstance(loss_balancer, GradNorm):
                # GradNorm 返回总损失和梯度范数损失
                total_loss, grad_norm_loss = loss_balancer(model, task_losses)
                # 将梯度范数损失也加入总损失（用于更新任务权重）
                total_loss = total_loss + grad_norm_loss
            else:
                # 不确定性加权等方法直接返回加权后的总损失
                total_loss = loss_balancer(task_losses)
            
            # ========== 反向传播 ==========
            optimizer.zero_grad()  # 清零梯度
            total_loss.backward()  # 反向传播计算梯度
            optimizer.step()       # 更新参数
            
            # 累积总损失
            epoch_total_loss += total_loss.item()
        
        # ========== 训练日志 ==========
        # 打印每个 epoch 的训练信息
        avg_total_loss = epoch_total_loss / len(dataloader)
        avg_task_losses = [loss / len(dataloader) for loss in epoch_task_losses]
        
        print(f"Epoch {epoch+1}/{num_epochs}, Total Loss: {avg_total_loss:.4f}")
        for i, task_loss in enumerate(avg_task_losses):
            task_name = model.task_names[i] if hasattr(model, 'task_names') else f"Task {i+1}"
            print(f"  {task_name} Loss: {task_loss:.4f}")
        
        # 如果使用不确定性加权，打印学习到的不确定性参数
        if isinstance(loss_balancer, UncertaintyWeighting):
            sigmas = torch.exp(loss_balancer.log_sigma).detach().cpu().numpy()
            print(f"  Task Uncertainties (σ): {sigmas}")
        
        # 如果使用 GradNorm，打印学习到的任务权重
        if isinstance(loss_balancer, GradNorm):
            weights = loss_balancer.task_weights.detach().cpu().numpy()
            print(f"  Task Weights: {weights}")
    
    return model

# 使用示例
model = MMoE(
    input_dim=100,
    num_experts=4,
    expert_hidden_dim=64,
    task_hidden_dims=[32, 16],
    num_tasks=2,
    dropout=0.1
)
model.task_names = ['ctr', 'cvr']  # 设置任务名称

loss_balancer = UncertaintyWeighting(num_tasks=2)
trained_model = train_multi_task_model(
    model, dataloader, num_epochs=10, lr=0.001,
    loss_balancer=loss_balancer
)

评估指标

多任务学习的评估与单任务学习不同，需要同时评估所有任务的性能。评估时需要注意：

  1. 任务特定指标：每个任务可能有不同的评估指标（如 CTR 用 AUC， CVR 用 AUC，回归任务用 MSE）
  2. 标签缺失处理：某些任务（如 CVR）可能只在部分样本上有标签，需要正确处理
  3. 综合评估：需要综合考虑所有任务的性能，不能只看单一任务

下面我们实现一个通用的多任务模型评估函数，支持多种评估指标和标签缺失处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
from sklearn.metrics import roc_auc_score, log_loss

def evaluate_multi_task_model(model, dataloader, task_names, device='cuda'):
    """
    评估多任务模型
    
    这个函数实现了多任务学习的完整评估流程，包括：
    1. 收集所有任务的预测和标签
    2. 处理标签缺失（某些任务可能只在部分样本上有标签）
    3. 计算每个任务的评估指标
    4. 返回所有任务的评估结果
    
    Args:
        model: 多任务模型，需要支持前向传播返回多个任务的预测
        dataloader: 数据加载器，每个 batch 包含 features 和所有任务的标签
        task_names: 任务名称列表，如['ctr', 'cvr']
        device: 评估设备，'cuda'或'cpu'
    
    Returns:
        metrics: 评估指标字典，格式为 {task_name: {metric_name: value }}
                例如：{'ctr': {'AUC': 0.75, 'LogLoss': 0.45}, 
                      'cvr': {'AUC': 0.68, 'LogLoss': 0.32 }}
    """
    # 设置为评估模式（禁用 Dropout 等）
    model.eval()
    
    # 初始化存储所有预测和标签的字典
    all_outputs = {task: [] for task in task_names}
    all_labels = {task: [] for task in task_names}
    
    # 第一步：收集所有 batch 的预测和标签
    with torch.no_grad():  # 禁用梯度计算，节省内存和计算
        for batch in dataloader:
            # 提取特征并移到指定设备
            features = batch['features'].float().to(device)
            
            # 前向传播，获取所有任务的预测
            # outputs 是一个列表，每个元素对应一个任务的预测
            outputs = model(features)
            
            # 存储每个任务的预测和标签
            for i, task in enumerate(task_names):
                # 将预测从 GPU 移到 CPU 并转换为 numpy 数组
                all_outputs[task].extend(outputs[i].cpu().numpy())
                # 存储标签（假设标签在 batch 中，键名为任务名）
                all_labels[task].extend(batch[task].numpy())
    
    # 第二步：计算每个任务的评估指标
    metrics = {}
    for task in task_names:
        # 将列表转换为 numpy 数组
        outputs = np.array(all_outputs[task]).squeeze()  # 移除多余的维度
        labels = np.array(all_labels[task])
        
        # 处理标签缺失：某些任务（如 CVR）可能只在部分样本上有标签
        # 假设-1 表示无标签（可以根据实际情况调整）
        valid_mask = labels >= 0
        
        # 只计算有标签的样本的指标
        if valid_mask.sum() > 0:
            valid_outputs = outputs[valid_mask]
            valid_labels = labels[valid_mask]
            
            # 计算 AUC（ Area Under ROC Curve）
            # AUC 衡量模型区分正负样本的能力，范围[0, 1]，越大越好
            auc = roc_auc_score(valid_labels, valid_outputs)
            
            # 计算 LogLoss（对数损失）
            # LogLoss 衡量预测概率与真实标签的差异，越小越好
            # 注意：如果 outputs 是 logit，需要先转换为概率
            # 使用 sigmoid 函数： prob = 1 / (1 + exp(-logit))
            probs = 1 / (1 + np.exp(-valid_outputs))
            logloss = log_loss(valid_labels, probs)
            
            # 存储该任务的评估指标
            metrics[task] = {'AUC': auc, 'LogLoss': logloss}
        else:
            # 如果没有有效标签，记录为 NaN
            metrics[task] = {'AUC': np.nan, 'LogLoss': np.nan}
    
    return metrics

# 使用示例
metrics = evaluate_multi_task_model(trained_model, dataloader, ['ctr', 'cvr'])
for task, task_metrics in metrics.items():
    print(f"{task}: AUC={task_metrics['AUC']:.4f}, LogLoss={task_metrics['LogLoss']:.4f}")

样本平衡策略

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def balance_multi_task_samples(features, labels_dict, target_ratio=1.0):
    """
    平衡多任务样本量
    Args:
        features: 特征矩阵
        labels_dict: 标签字典
        target_ratio: 目标样本比例（相对于最大任务）
    Returns:
        balanced_features, balanced_labels_dict
    """
    # 计算各任务的样本量
    task_sizes = {task: len(labels) for task, labels in labels_dict.items()}
    max_size = max(task_sizes.values())
    target_size = int(max_size * target_ratio)
    
    # 对每个任务进行采样
    balanced_indices = []
    for task, labels in labels_dict.items():
        task_indices = np.arange(len(labels))
        if len(task_indices) > target_size:
            # 下采样
            sampled_indices = np.random.choice(task_indices, target_size, replace=False)
        else:
            # 上采样（有放回）
            sampled_indices = np.random.choice(task_indices, target_size, replace=True)
        balanced_indices.append(sampled_indices)
    
    # 合并索引（简化：使用第一个任务的索引）
    # 实际应用中需要更复杂的合并策略
    final_indices = balanced_indices[0]
    
    balanced_features = features[final_indices]
    balanced_labels_dict = {task: labels[final_indices] 
                           for task, labels in labels_dict.items()}
    
    return balanced_features, balanced_labels_dict

动态权重调整

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class DynamicWeightAdjuster:
    """动态权重调整器"""
    
    def __init__(self, num_tasks, initial_weights=None, alpha=0.1):
        """
        Args:
            num_tasks: 任务数量
            initial_weights: 初始权重，如果为 None 则均匀分配
            alpha: 权重更新速率
        """
        self.num_tasks = num_tasks
        self.alpha = alpha
        if initial_weights is None:
            self.weights = torch.ones(num_tasks) / num_tasks
        else:
            self.weights = torch.tensor(initial_weights)
        
        # 记录历史性能
        self.task_performances = {i: [] for i in range(num_tasks)}
    
    def update(self, task_performances):
        """
        根据任务性能更新权重
        Args:
            task_performances: 各任务的性能指标（越大越好）， list of floats
        """
        task_performances = torch.tensor(task_performances)
        
        # 归一化性能
        normalized_perf = task_performances / (task_performances.sum() + 1e-8)
        
        # 更新权重：性能好的任务权重增加
        self.weights = (1 - self.alpha) * self.weights + self.alpha * normalized_perf
        
        # 归一化权重
        self.weights = self.weights / (self.weights.sum() + 1e-8)
        
        return self.weights.numpy()
    
    def get_weights(self):
        """获取当前权重"""
        return self.weights.numpy()

模型对比工具

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def compare_models(models_dict, dataloader, task_names, device='cuda'):
    """
    对比多个模型的性能
    Args:
        models_dict: 模型字典，{model_name: model}
        dataloader: 数据加载器
        task_names: 任务名称列表
        device: 设备
    Returns:
        comparison_results: 对比结果字典
    """
    comparison_results = {}
    
    for model_name, model in models_dict.items():
        model = model.to(device)
        metrics = evaluate_multi_task_model(model, dataloader, task_names, device)
        comparison_results[model_name] = metrics
    
    # 打印对比结果
    print("Model Comparison Results:")
    print("-" * 80)
    for task in task_names:
        print(f"\n{task}:")
        for model_name, metrics in comparison_results.items():
            if task in metrics:
                print(f"  {model_name}: AUC={metrics[task]['AUC']:.4f}, "
                      f"LogLoss={metrics[task]['LogLoss']:.4f}")
    
    return comparison_results

# 使用示例
models_to_compare = {
    'SharedBottom': SharedBottom(input_dim=100, shared_hidden_dims=[64], 
                                task_hidden_dims=[32], num_tasks=2),
    'MMoE': MMoE(input_dim=100, num_experts=4, expert_hidden_dim=64,
                task_hidden_dims=[32], num_tasks=2),
    'PLE': PLE(input_dim=100, num_layers=2, num_shared_experts=2,
               num_task_specific_experts=2, expert_hidden_dim=64,
               task_hidden_dims=[32], num_tasks=2)
}

comparison_results = compare_models(models_to_compare, dataloader, ['ctr', 'cvr'])

特征重要性分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def analyze_feature_importance(model, dataloader, feature_names, task_idx=0, device='cuda'):
    """
    分析特征重要性（简化版本，使用梯度）
    Args:
        model: 多任务模型
        dataloader: 数据加载器
        feature_names: 特征名称列表
        task_idx: 要分析的任务索引
        device: 设备
    Returns:
        feature_importance: 特征重要性字典
    """
    model.eval()
    feature_gradients = {name: [] for name in feature_names}
    
    for batch in dataloader:
        features = batch['features'].float().to(device)
        features.requires_grad = True
        
        outputs = model(features)
        loss = F.binary_cross_entropy_with_logits(
            outputs[task_idx].squeeze(), 
            batch[list(batch.keys())[task_idx+1]].float().to(device)
        )
        
        # 计算梯度
        gradients = torch.autograd.grad(loss, features, retain_graph=False)[0]
        
        # 累积梯度绝对值
        for i, name in enumerate(feature_names):
            feature_gradients[name].append(torch.abs(gradients[:, i]).mean().item())
    
    # 计算平均重要性
    feature_importance = {name: np.mean(grads) 
                         for name, grads in feature_gradients.items()}
    
    # 排序
    feature_importance = dict(sorted(feature_importance.items(), 
                                    key=lambda x: x[1], reverse=True))
    
    return feature_importance

# 使用示例
feature_names = [f'feature_{i}' for i in range(100)]
importance = analyze_feature_importance(trained_model, dataloader, 
                                       feature_names, task_idx=0)
print("Top 10 Important Features:")
for i, (feature, imp) in enumerate(list(importance.items())[:10]):
    print(f"{i+1}. {feature}: {imp:.4f}")

Q&A：常见问题解答

Q1: 多任务学习和单任务学习相比，性能一定更好吗？

A: 不一定。多任务学习的性能提升取决于任务间的相关性： - 当任务高度相关时，多任务学习通常能提升性能 - 当任务冲突或相关性很低时，可能出现负迁移，性能下降 - 需要根据任务特点选择合适的架构（如 PLE 处理负迁移）

Q2: 如何选择多任务学习的架构？

A: 架构选择需要考虑： - 任务相关性：高度相关用 Shared-Bottom，存在冲突用 MMoE/PLE - 样本量差异：样本量差异大时， MMoE/PLE 的灵活性更好 - 计算资源： Shared-Bottom 最简单， PLE 最复杂 - 业务需求： ESMM 专门解决 CVR 样本选择偏差问题

Q3: 如何平衡不同任务的损失？

A: 常见方法： - 固定权重：简单但需要调参 - 不确定性加权：可学习权重，适合大多数场景 - GradNorm：动态平衡梯度，适合任务差异大的场景 - 动态权重：根据任务性能调整，需要设计调整策略

Q4: ESMM 中的 CVR 为什么通过 CTCVR/CTR 计算，而不是直接预测？

A: 原因： - 样本选择偏差： CVR 只在点击样本上有标签，但推理时需要预测所有样本 - 数据稀疏： CVR 样本量远小于 CTR，直接预测容易过拟合 - 概率一致性： CTCVR = CTR × CVR，通过除法保证概率关系一致

Q5: MMoE 中的专家数量如何选择？

A: 专家数量选择： - 任务数量：通常专家数量 >= 任务数量 - 任务复杂度：复杂任务需要更多专家 - 计算资源：专家数量影响计算量 - 经验值：通常 2-8 个专家，可以通过实验选择

Q6: PLE 相比 MMoE 的优势在哪里？

A: PLE 的优势： - 解决负迁移：任务特定专家避免任务冲突 - 缓解跷跷板现象：渐进式分层允许任务在不同层次共享 - 更好的任务平衡：共享专家和任务特定专家的组合更灵活

Q7: 如何处理任务样本量差异很大的情况？

A: 处理方法： - 样本采样：对样本量大的任务进行下采样，平衡样本量 - 损失加权：给样本量小的任务更大的权重 - 课程学习：先训练样本量大的任务，再逐步加入小样本任务 - 数据增强：对样本量小的任务进行数据增强

Q8: 多任务学习中的负迁移如何检测和解决？

A: 检测和解决： - 检测：对比单任务和多任务性能，如果多任务性能下降，可能存在负迁移 - 解决： - 使用 MMoE/PLE 等架构，减少任务间的强制共享 - 增加任务特定参数，减少共享参数 - 调整损失权重，降低冲突任务的权重

Q9: 多任务学习的线上服务如何部署？

A: 部署考虑： - 模型大小：多任务模型通常比多个单任务模型小 - 推理延迟：共享底层计算，延迟可能更低 - A/B 测试：需要同时评估多个任务的性能 - 监控指标：需要监控所有任务的性能指标

Q10: 如何评估多任务学习的效果？

A: 评估方法： - 单任务指标：每个任务的 AUC 、 LogLoss 等 - 综合指标：多个任务的加权平均 - 业务指标： CTR 、 CVR 、 GMV 等业务指标 - 对比实验：与单任务模型、其他多任务模型对比

Q11: 多任务学习可以用于哪些推荐场景？

A: 适用场景： - 电商推荐： CTR 、 CVR 、 GMV 等多目标 - 内容推荐：点击、播放时长、完播率、互动等 - 广告推荐： CTR 、 CVR 、 ROI 等 - 社交推荐：点击、关注、互动等

Q12: 多任务学习的未来发展方向？

A: 发展方向： - 自动架构搜索：自动设计多任务架构 - 任务关系学习：更好地建模任务关系 - 可解释性：理解任务间的知识共享机制 - 在线学习：支持任务的动态添加和删除 - 跨域迁移：不同领域间的任务迁移

总结

多任务学习是推荐系统中的重要技术，通过共享底层特征表示，可以同时优化多个业务目标，提升模型性能和降低维护成本。从 Shared-Bottom 到 ESMM 、 MMoE 、 PLE，多任务学习架构不断演进，解决了样本选择偏差、负迁移、任务冲突等关键问题。

在实际应用中，需要根据任务特点选择合适的架构，平衡不同任务的损失，处理样本分布差异，才能充分发挥多任务学习的优势。随着研究的深入，多任务学习将在推荐系统中发挥越来越重要的作用。

  • 本文标题：推荐系统（九）—— 多任务学习与多目标优化
  • 本文作者：Chen Kai
  • 创建时间：2024-06-11 09:45:00
  • 本文链接：https://www.chenk.top/%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%EF%BC%88%E4%B9%9D%EF%BC%89%E2%80%94%E2%80%94-%E5%A4%9A%E4%BB%BB%E5%8A%A1%E5%AD%A6%E4%B9%A0%E4%B8%8E%E5%A4%9A%E7%9B%AE%E6%A0%87%E4%BC%98%E5%8C%96/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
 评论