推荐系统（七）—— 图神经网络与社交推荐
Chen Kai BOSS
  2024-06-01 10:30:00 2024-06-01 10:30      11.3k 字  48 分钟  

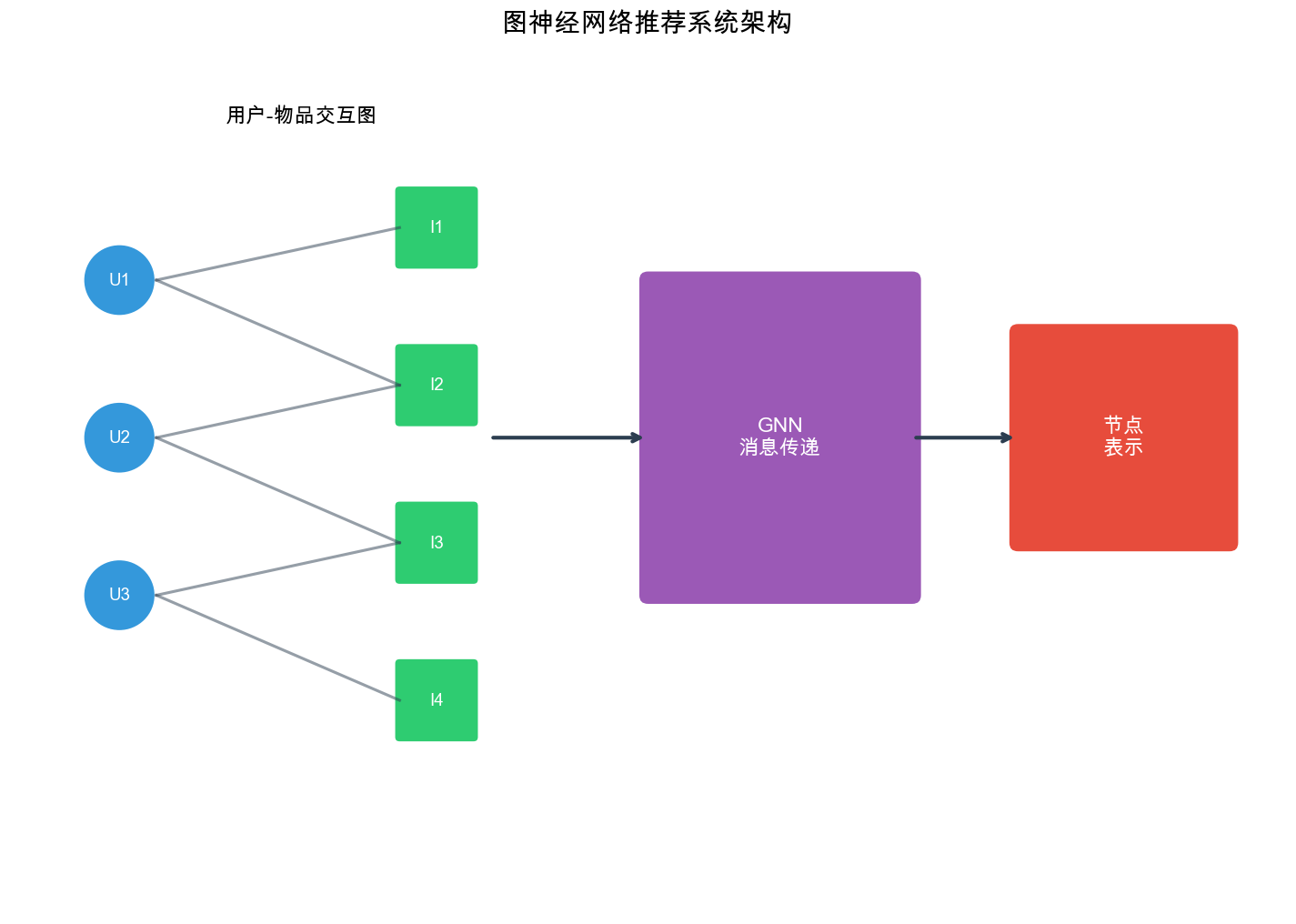
在推荐系统中，用户和物品之间的关系天然地构成了一个图结构：用户与物品之间的交互形成边，用户与用户之间的社交关系也形成边，物品与物品之间的相似性同样可以建模为边。传统的协同过滤和矩阵分解方法虽然有效，但它们往往将这种图结构信息"扁平化"处理，丢失了丰富的结构信息。

图神经网络（ Graph Neural Networks, GNN）的出现，为推荐系统带来了新的可能性。 GNN 能够直接在图上进行信息传播和聚合，捕捉用户和物品之间的高阶关系，从而学习到更丰富的表示。从 Pinterest 的 PinSage 到阿里巴巴的 LightGCN，从神经图协同过滤 NGCF 到社交推荐系统， GNN 在推荐领域展现出了强大的能力。

本文将深入探讨图神经网络在推荐系统中的应用，从 GNN 的基础原理（ GCN 、 GAT 、 GraphSAGE）开始，逐步深入到推荐场景中的图建模、经典模型实现、社交推荐，以及图采样和训练技巧。我们会提供完整的代码实现，帮助读者从理论到实践全面掌握这一技术。

图神经网络基础

图的基本概念

在深入 GNN 之前，需要先理解图的基本概念。

什么是图（ Graph）？

直觉理解： 图是一种描述"关系网络"的数据结构。它由两部分组成：

  1. 节点（ Node/Vertex）：网络中的实体
    • 例如：社交网络中的人、推荐系统中的用户/物品、知识图谱中的概念
  2. 边（ Edge）：节点之间的关系或连接
    • 例如：社交网络中的好友关系、推荐系统中的点击/购买行为、知识图谱中的"属于"关系

生活中的例子：

  • 社交网络：微信好友关系
    • 节点 = 用户
    • 边 = 好友连接
  • 地图导航：城市交通网络
    • 节点 = 城市
    • 边 = 道路/航线
  • 推荐系统：用户-物品交互
    • 节点 = 用户 + 物品
    • 边 = 点击/购买/评分

形式化表示

图 由节点集合 和边集合 组成，形式化表示为 ：

  • 是节点集合（ 个节点）
  • 是边集合（节点对的集合）

符号说明：

  • ：图中有 个节点
  • ：图中有 条边
  • ：表示节点 和 之间有连接

在推荐系统中，常见的图结构包括：

用户-物品二部图（ Bipartite Graph）：

  • 节点：用户节点 和物品节点 - 例如：用户={Alice, Bob, Carol}，物品={电影 A, 电影 B, 电影 C}
  • 边：用户与物品之间的交互（点击、购买、评分等）
    • 例如： Alice 点击了电影 A， Bob 购买了电影 B
  • 特点：用户节点之间没有直接连接，物品节点之间也没有直接连接
    • 这叫"二部图"：节点分为两组，边只连接不同组的节点

为什么是二部图？

在推荐场景中：

  • 用户不会直接"连接"另一个用户（虽然可能有社交关系，但那是另一个图）
  • 物品不会直接"连接"另一个物品（虽然可能相似，但边表示的是交互）
  • 边总是"用户→物品"或"物品→用户"

社交图（ Social Graph）：

  • 节点：用户
  • 边：用户之间的关注、好友关系
  • 特点：通常是无向图（双向好友）或有向图（单向关注）

知识图谱（ Knowledge Graph）：

  • 节点：实体（用户、物品、属性等）
  • 边：实体之间的关系（如"喜欢"、"属于"、"相似"等）
  • 特点：包含多种类型的节点和边（异构图）

邻接矩阵（ Adjacency Matrix）：图 的邻接矩阵 Extra close brace or missing open braceA \in \{0,1} ^{n \times n} 定义为：

$$

A_{ij} = （有边连接）（无边连接）

$$

直觉理解：

邻接矩阵是一个 的表格：

  • 行 列 的值为 1，表示节点 和节点 之间有连接
  • 值为 0 表示无连接

例子： 假设有 4 个节点，边集合为 邻接矩阵为：

$$

A =

$$

性质：

  • 对于无向图， 是对称矩阵（）
  • 对于有向图， 可能不对称
  • 对角线通常为 0（节点不连接自己），但添加自连接时可以为 1

度（ Degree）：节点 的度 表示与它相连的边的数量：

$$

d_i = {j=1}^{n} A{ij}$$

直觉： 度表示节点的"连接数"或"流行度"

  • 社交网络中：度高的用户有很多好友（社交达人）
  • 推荐系统中：度高的物品被很多用户交互过（热门物品）

度矩阵（ Degree Matrix）：对角矩阵 ，其中 ：

$$

D =

$$

作用： 度矩阵用于归一化邻接矩阵，防止度大的节点主导信息传播。

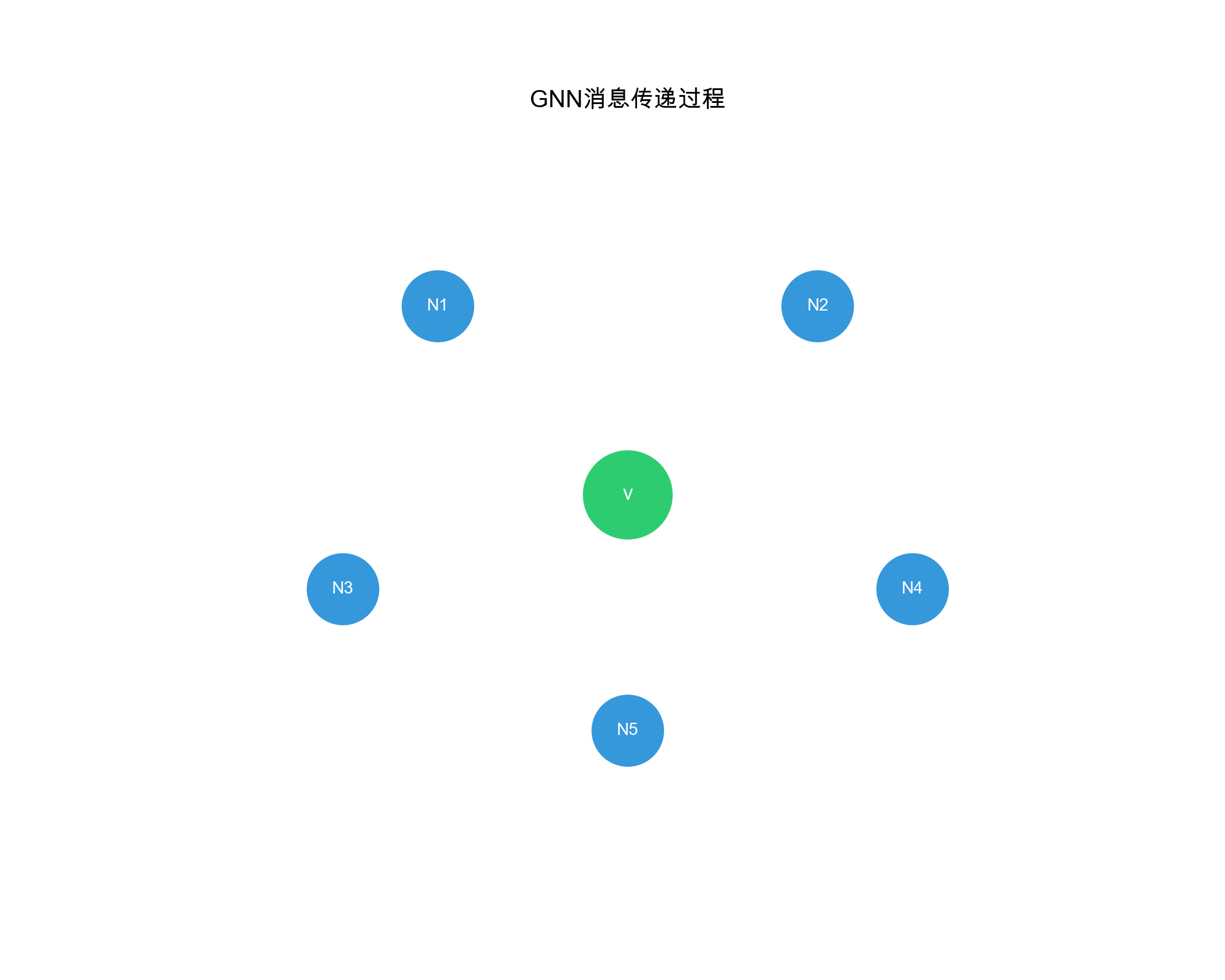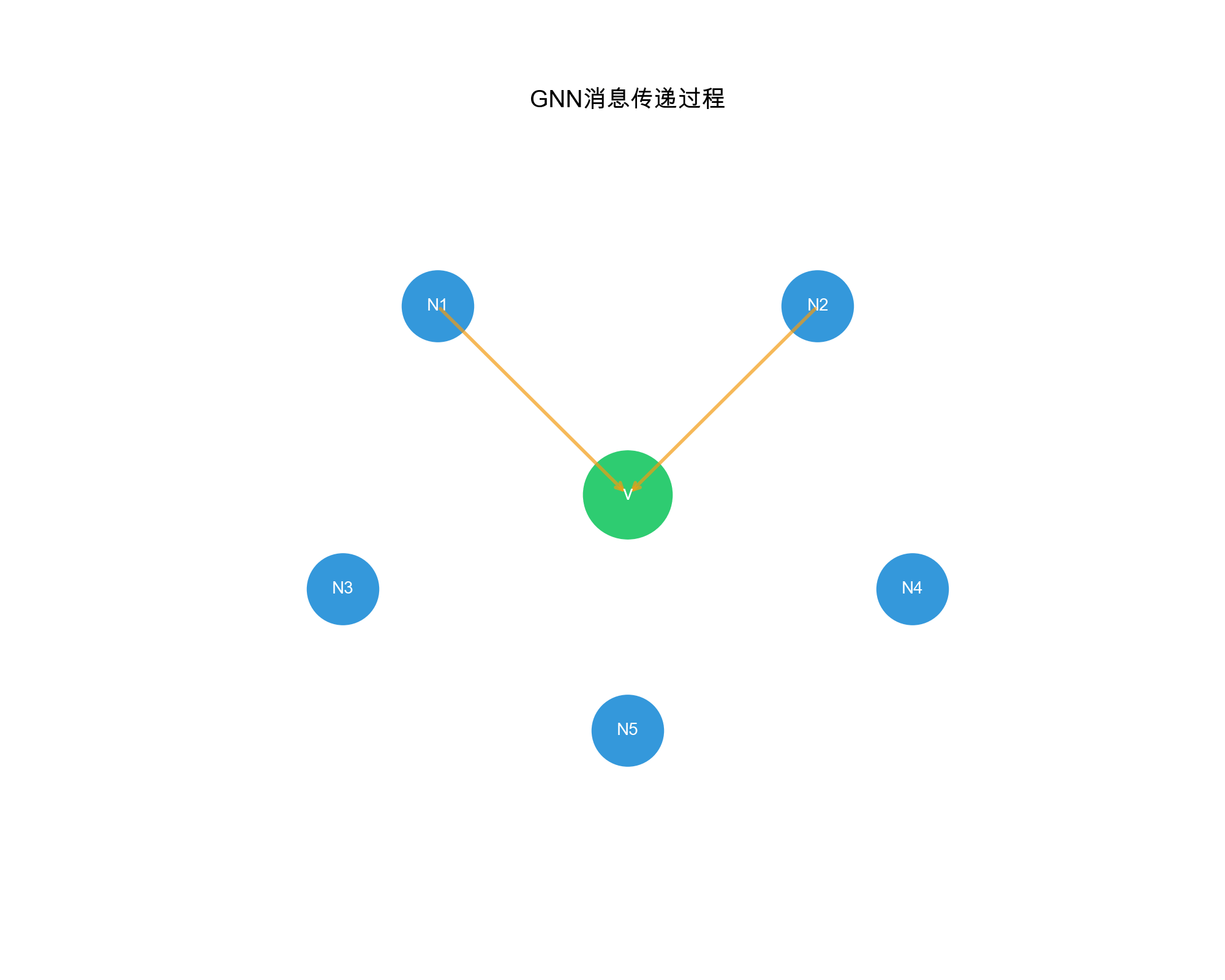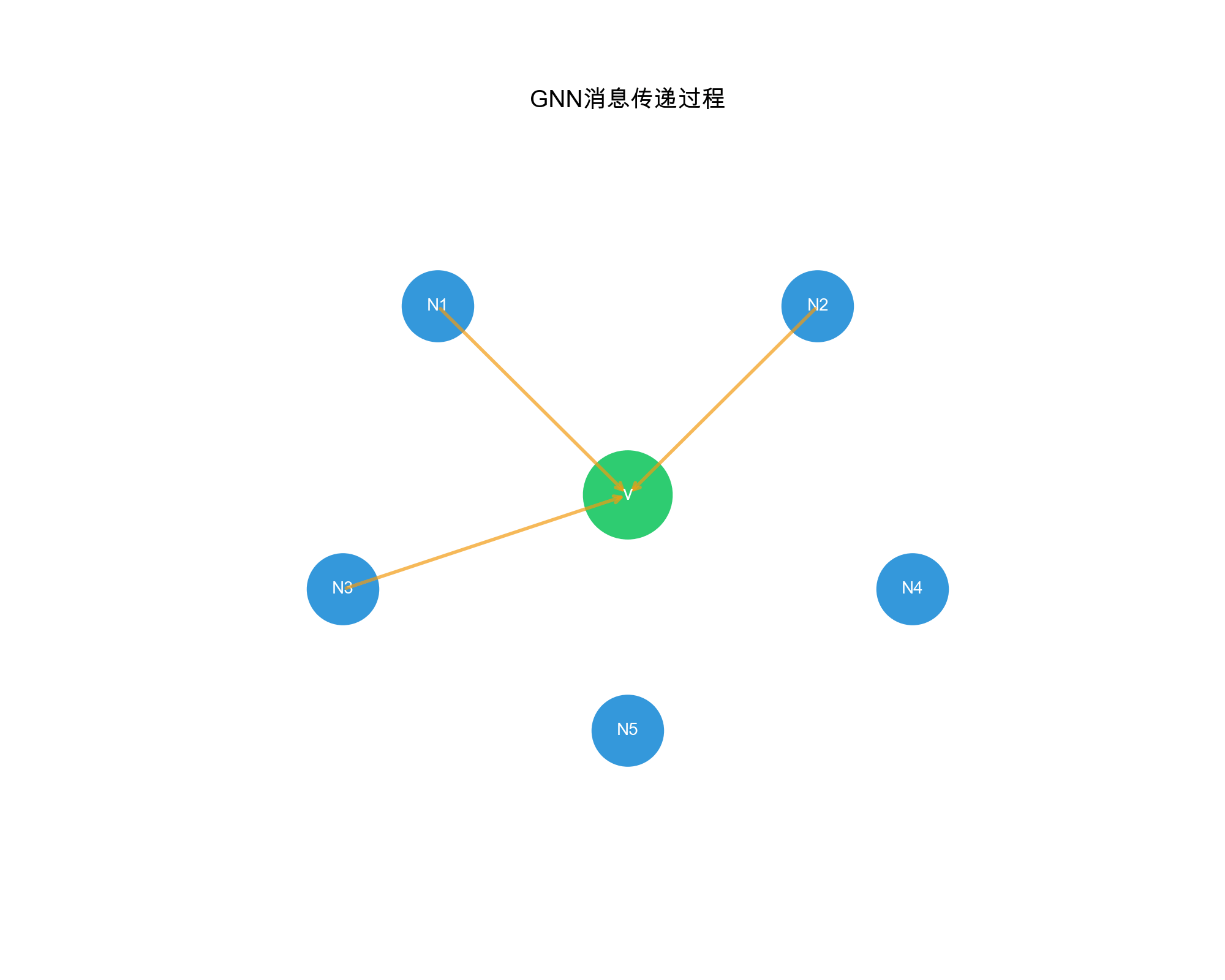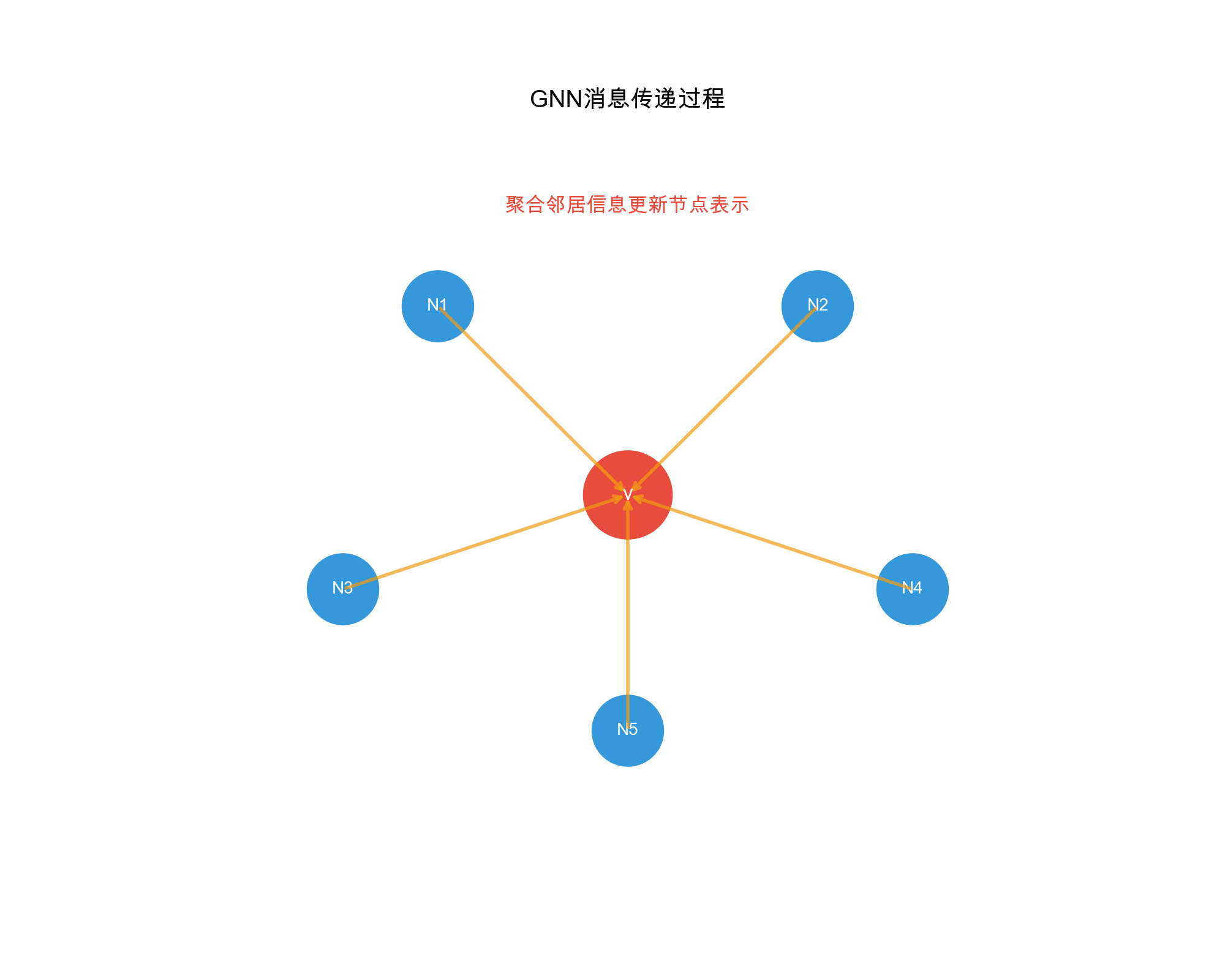
图神经网络的核心思想

图神经网络的核心思想是消息传递（ Message Passing）：每个节点通过聚合邻居节点的信息来更新自己的表示。

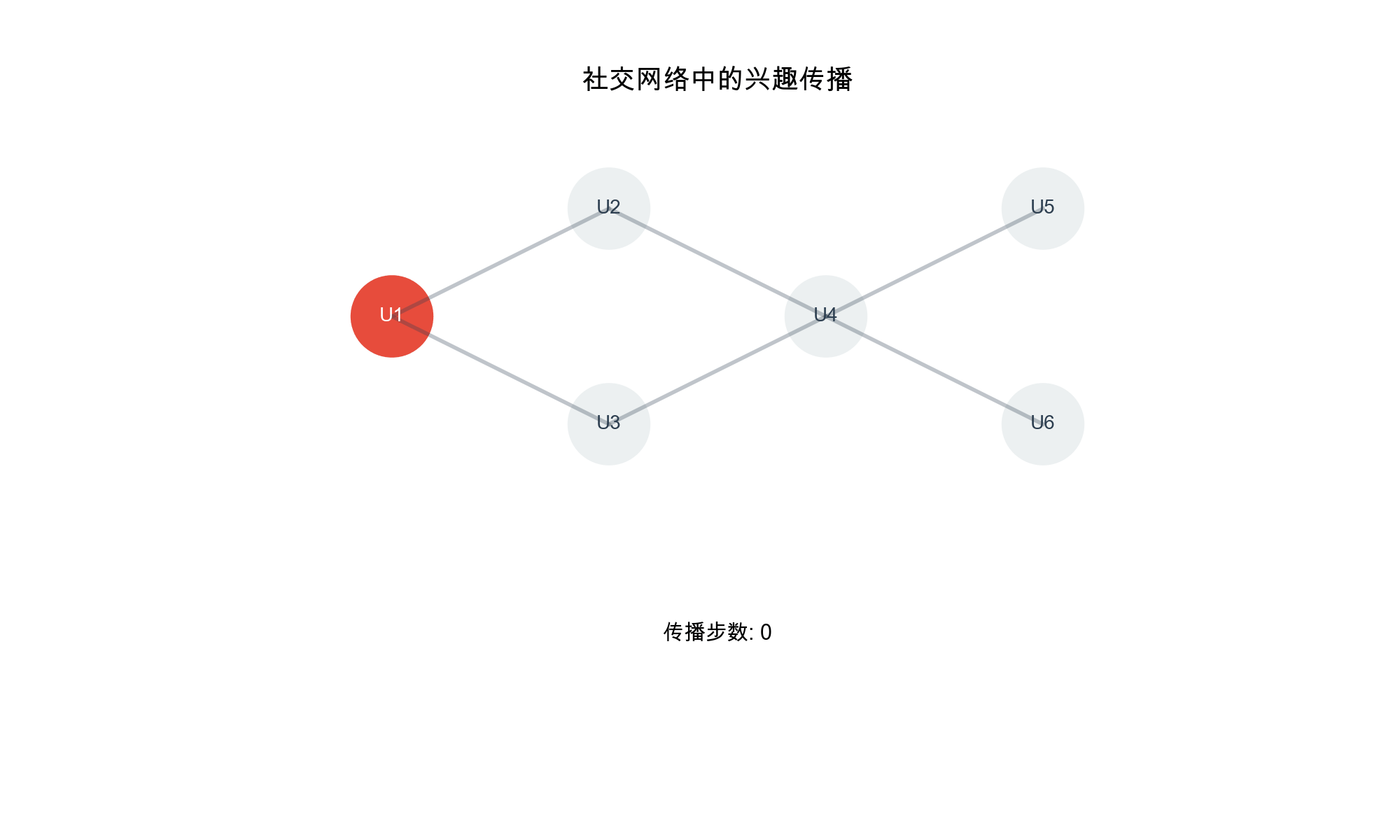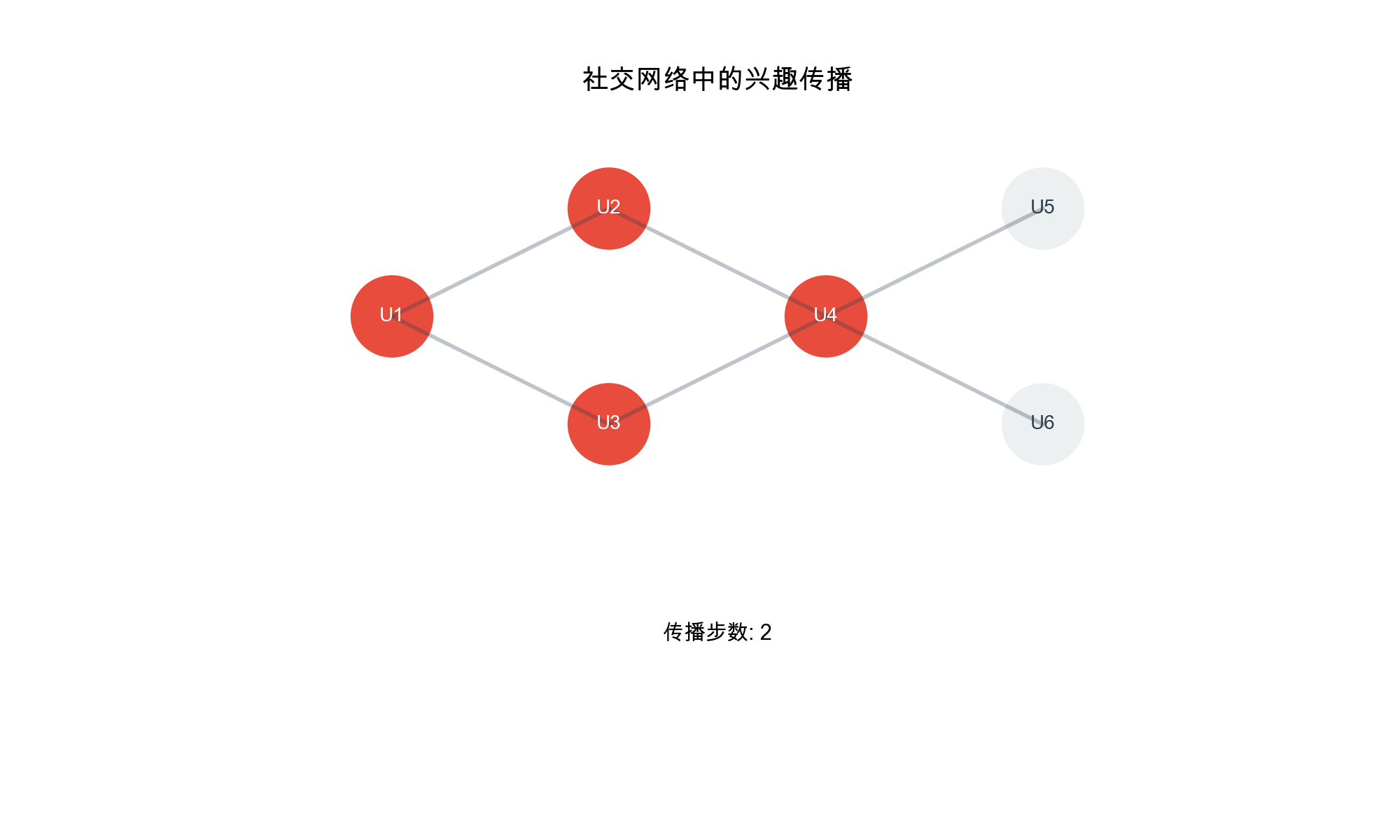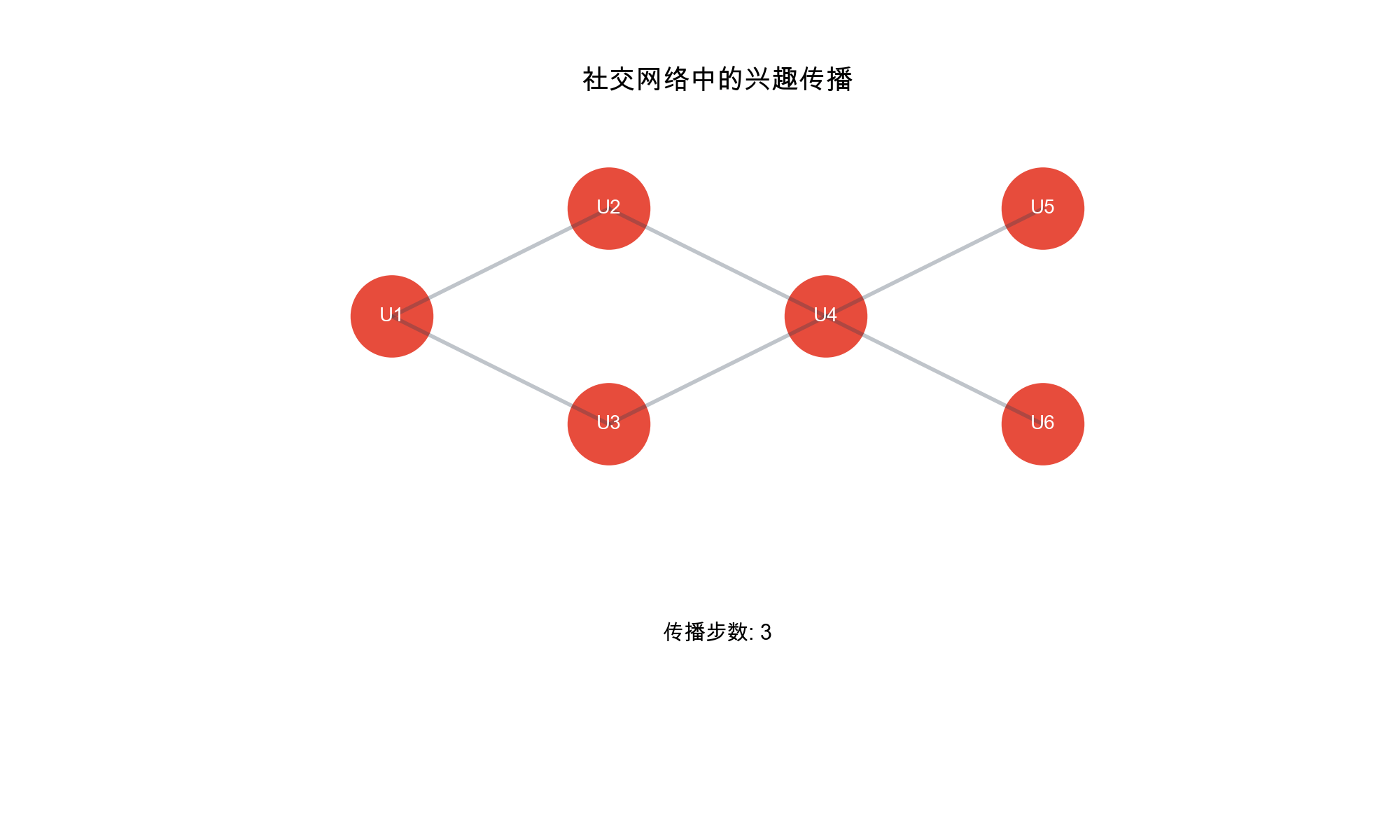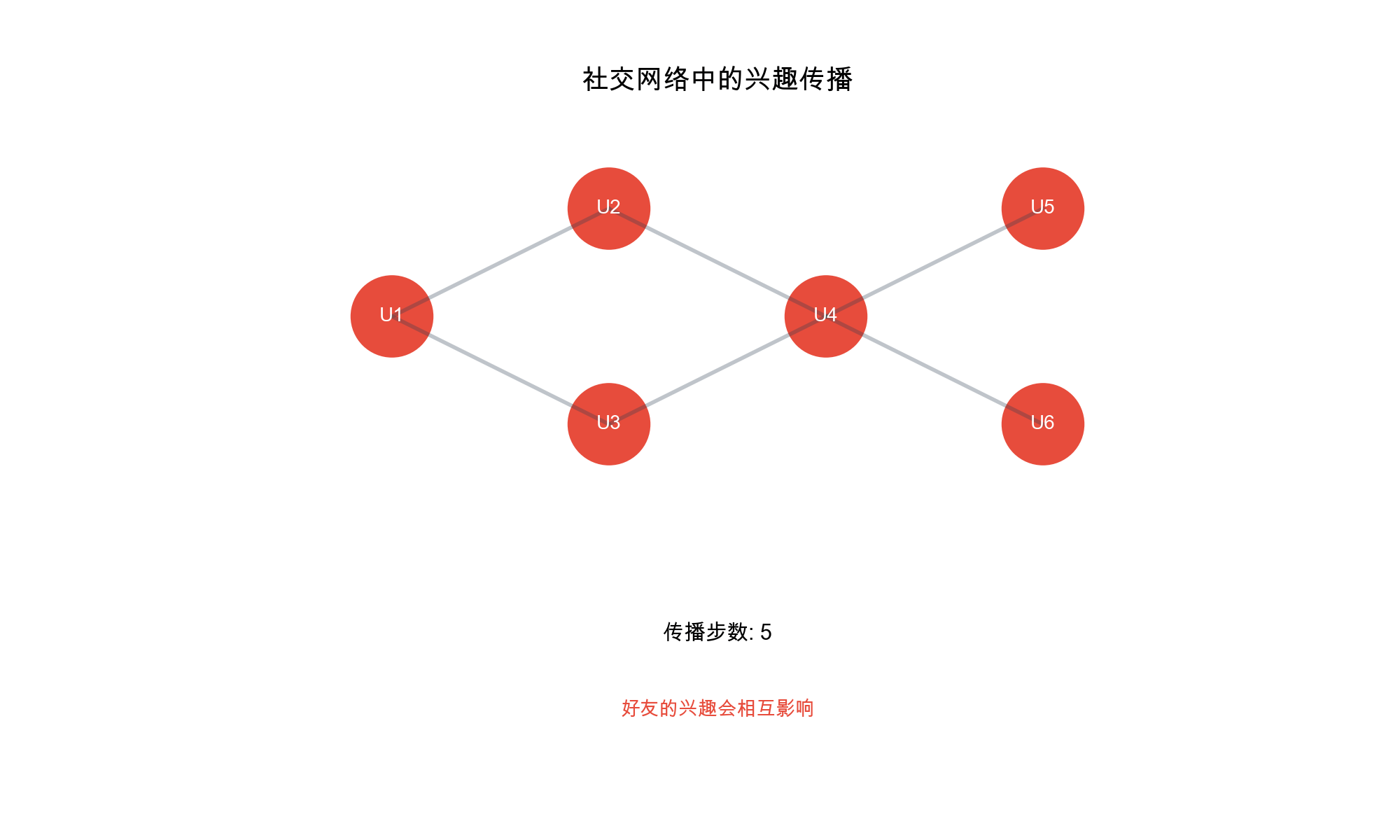
直觉：社交网络中的信息传播

想象你在社交网络上：

  1. 初始状态：每个人有自己的兴趣（节点特征）
    • Alice 喜欢电影
    • Bob 喜欢音乐
    • Carol 喜欢运动
  2. 消息传递：你会受到好友的影响
    • Alice 看到 Bob 在听音乐，开始对音乐感兴趣
    • Bob 看到 Carol 在运动，也想尝试运动
    • 经过多次交流，大家的兴趣逐渐融合
  3. 更新表示：每个人的兴趣变成了自己+好友兴趣的混合
    • Alice 现在喜欢：电影（主要）+ 音乐（来自 Bob）
    • Bob 现在喜欢：音乐（主要）+ 电影（来自 Alice）+ 运动（来自 Carol）

这就是 GNN 的核心：通过邻居的信息丰富自己的表示。

为什么这样有用？

在推荐系统中：

  • 用户节点：如果两个用户交互过相似的物品（有共同邻居），他们可能有相似的偏好
  • 物品节点：如果两个物品被相似的用户喜欢（有共同邻居），它们可能相似

通过消息传递， GNN 可以捕捉这种高阶相似性：

  • 1 阶：用户直接交互的物品（协同过滤已经能做）
  • 2 阶：交互过相似物品的其他用户喜欢的物品（"买了 A 的人也买了 B"）
  • 3 阶及更高：更复杂的关联模式

形式化定义

GNN 的每一层执行以下操作：

  1. 消息生成（ Message）：每个节点生成发送给邻居的消息
  2. 消息聚合（ Aggregate）：每个节点聚合来自邻居的消息
  3. 节点更新（ Update）：根据聚合的消息更新节点表示

对于节点 ，其第 层的表示 计算为：

Extra close brace or missing open brace\mathbf{h}_v^{(l+1)} = \text{UPDATE}^{(l)}\left(\mathbf{h}_v^{(l)}, \text{AGGREGATE}^{(l)}\left(\{\mathbf{h}_u^{(l)} : u \in \mathcal{N}(v)} \right)\right)

符号说明：

  • ：节点 在第 层的表示（ 维向量）
  • ：节点 的邻居集合
    • 例如：用户 Alice 的邻居 = 她交互过的所有物品
  • ：聚合函数，将邻居信息汇总
    • 常见方法：求和（ SUM）、平均（ MEAN）、最大值（ MAX）
  • ：更新函数，结合自己和邻居信息更新表示
    • 通常是神经网络（如 MLP 、 GRU）

直觉理解（推荐场景）：

假设我们要更新用户 Alice 的表示：

  1. 第 0 层：初始嵌入（随机初始化或从 ID 学习）
    $_{} ^{(0)} = [0.1, 0.2, -0.3, ]第层：聚合交互过的物品的信息邻居：电影、电影、电影聚合：(_A^{(0)}, _B^{(0)}, _C^{(0)})$ - 更新：邻居聚合 - 含义： Alice 的表示现在包含了她喜欢的电影的信息

  2. 第 2 层：再次聚合，这次邻居的表示已经包含了它们的邻居信息

    • 电影 A 的表示 已经包含了"喜欢电影 A 的其他用户"的信息
    • Alice 的 2 层表示包含了"喜欢相似电影的其他用户"的信息
    • 含义：捕捉到了 2 阶相似性

为什么多层有用？

  • 1 层：直接邻居（用户喜欢的物品）
  • 2 层：邻居的邻居（喜欢相似物品的用户喜欢的其他物品）
  • 3 层：更高阶的关联模式

但也不是越多越好：

  • 过多层：导致过平滑（所有节点表示变得相似），丧失个性化
  • 通常： 2-3 层就足够了

图卷积网络（ GCN）

图卷积网络（ Graph Convolutional Network, GCN）是 GNN 的经典模型之一，由 Kipf & Welling 在 2017 年提出。

为什么需要 GCN？（动机）

传统神经网络（ CNN 、 RNN）处理的是规则结构数据：

  • CNN：图像（规则的 2D 网格）
  • RNN：序列（有固定的前后关系）

但图数据是不规则的：

  • 每个节点的邻居数量不同（有的用户交互了 10 个物品，有的交互了 1000 个）
  • 没有固定的顺序（邻居没有"第一个"、"第二个"的概念）

GCN 的目标：设计一种在图上做"卷积"的操作，能够：

  1. 聚合邻居信息（类似 CNN 的感受野）
  2. 处理任意数量的邻居
  3. 对邻居顺序不敏感（置换不变性）

GCN 的数学形式：

GCN 使用对称归一化的邻接矩阵进行信息传播：

符号说明：

  • ：添加了自连接的邻接矩阵

    • ：原始邻接矩阵
    • ：单位矩阵（对角线为 1）
    • 作用：让每个节点在聚合时也包含自己的信息

  • ： 的度矩阵

    • （第 个节点的度，包括自连接）

  • ：第 层的节点表示矩阵

    • ：节点数量
    • $ d_l：第 l$ 层的特征维度
    • 第 行是节点 的表示向量

  • $^{(l)} ^{d_l d_{l+1}} ：可学习的权重矩阵将 d_l维特征映射到 d_{l+1}$ 维

  • ：激活函数（如 ReLU）

    • 引入非线性，提升表达能力

归一化的作用：Double exponent: use braces to clarify^{-} ^{-}

问题 1：不归一化会怎样？

如果直接用 ：

  • 度大的节点（邻居多）会获得更大的数值
    • 例如：节点 A 有 100 个邻居，节点 B 有 5 个邻居
    • A 聚合后的值是 B 的 20 倍！
  • 随着层数增加，数值会爆炸或消失
  • 训练不稳定

问题 2：为什么是 次方？

对称归一化 Double exponent: use braces to clarify^{-} ^{-} 的每个元素为：

直觉理解：

  • 当节点 和 相连时（），权重为
  • 度大的节点接收和发送的信息都会被"削弱"
  • 保证聚合后的数值范围稳定

为什么这样设计有效？

  1. 数值稳定：权重矩阵的特征值被限制在合理范围
  2. 信息均衡：度大的节点不会主导信息传播
  3. 理论保证：对应于图拉普拉斯矩阵的谱分解（与信号处理中的傅里叶变换类似）

节点级别的表示：

对于单个节点 ， GCN 的更新公式可以写为：

Extra close brace or missing open brace\mathbf{h}_v^{(l+1)} = \sigma\left(\sum_{u \in \mathcal{N}(v) \cup \{v} } \frac{1}{\sqrt{d_v d_u}} \mathbf{h}_u^{(l)} \mathbf{W}^{(l)}\right)

直觉理解（逐步拆解）：

  1. ：邻居 + 自己
    • 聚合邻居的同时保留自己的信息
  2. Extra close brace or missing open brace\sum_{u \in \mathcal{N}(v) \cup \{v} }：求和聚合
    • 简单但有效的聚合方式
  3. ：归一化权重
    • $ d_v：节点 v$ 的度（包括自连接）
    • $ d_u：节点 u$ 的度
    • 权重反比于度的平方根乘积
  4. ：先做特征变换
    • 将邻居特征投影到新的空间
  5. ：非线性激活
    • 提升模型的表达能力

完整流程示例：

假设用户 Alice（度=3）的邻居是电影 A（度=100）、电影 B（度=50）：

  1. 邻居权重：
    • 自己： - 电影 A： - 电影 B：$ = 0.082加权聚合：{} ^{} = 0.33 {} + 0.058 _A + 0.082 _B特征变换：乘以权重矩阵$4. 激活：
      应用 ReLU

关键洞察： 热门物品（度大）不会因为被很多用户喜欢而过度影响单个用户的表示。每个邻居的贡献被归一化了。

GCN 实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNLayer(nn.Module):
    """GCN 单层实现"""
    
    def __init__(self, in_channels, out_channels):
        super(GCNLayer, self).__init__()
        self.linear = nn.Linear(in_channels, out_channels)
        self.reset_parameters()
    
    def reset_parameters(self):
        nn.init.xavier_uniform_(self.linear.weight)
        nn.init.zeros_(self.linear.bias)
    
    def forward(self, x, edge_index):
        """
        Args:
            x: 节点特征矩阵 [num_nodes, in_channels]
            edge_index: 边索引 [2, num_edges]
        Returns:
            更新后的节点特征 [num_nodes, out_channels]
        """
        # 添加自连接
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
        
        # 计算度矩阵（行归一化）
        row, col = edge_index
        deg = degree(col, x.size(0), dtype=x.dtype)
        deg_inv_sqrt = deg.pow(-0.5)
        deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
        
        # 消息传递
        x = self.linear(x)
        x = self.propagate(edge_index, x=x, norm=norm)
        
        return x
    
    def message(self, x_j, norm):
        """消息函数：计算发送的消息"""
        return norm.view(-1, 1) * x_j

class GCN(nn.Module):
    """多层 GCN 模型"""
    
    def __init__(self, num_nodes, in_channels, hidden_channels, out_channels, num_layers=2, dropout=0.5):
        super(GCN, self).__init__()
        self.num_layers = num_layers
        self.dropout = dropout
        
        self.layers = nn.ModuleList()
        self.layers.append(GCNLayer(in_channels, hidden_channels))
        
        for _ in range(num_layers - 2):
            self.layers.append(GCNLayer(hidden_channels, hidden_channels))
        
        if num_layers > 1:
            self.layers.append(GCNLayer(hidden_channels, out_channels))
    
    def forward(self, x, edge_index):
        for i, layer in enumerate(self.layers):
            x = layer(x, edge_index)
            if i < len(self.layers) - 1:
                x = F.relu(x)
                x = F.dropout(x, p=self.dropout, training=self.training)
        return x

图注意力网络（ GAT）

图注意力网络（ Graph Attention Network, GAT）引入了注意力机制，允许节点自适应地选择重要的邻居进行信息聚合。

GAT 的核心思想：

GAT 为每条边 学习一个注意力权重 ，表示节点 对邻居 的关注程度。

注意力机制：

对于节点 和其邻居 ，注意力分数计算为：

$$

e_{vu} = (^T [_v || _u])$$

其中： - 是共享的线性变换矩阵 - 是可学习的注意力向量 - 表示拼接操作

然后使用 softmax 归一化得到注意力权重：

节点更新：

节点 的更新表示通过加权聚合邻居信息得到：

多头注意力：

GAT 通常使用多头注意力（ Multi-head Attention）来稳定训练并捕捉不同类型的邻居关系：

其中 是注意力头的数量， 表示拼接。

GAT 实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops

class GATLayer(nn.Module):
    """GAT 单层实现"""
    
    def __init__(self, in_channels, out_channels, heads=1, dropout=0.6, concat=True):
        super(GATLayer, self).__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.heads = heads
        self.concat = concat
        self.dropout = dropout
        
        # 线性变换
        self.W = nn.Parameter(torch.empty(size=(in_channels, out_channels * heads)))
        nn.init.xavier_uniform_(self.W.data, gain=1.414)
        
        # 注意力参数
        self.a = nn.Parameter(torch.empty(size=(2 * out_channels, 1)))
        nn.init.xavier_uniform_(self.a.data, gain=1.414)
        
        self.leaky_relu = nn.LeakyReLU(0.2)
    
    def forward(self, x, edge_index):
        """
        Args:
            x: 节点特征 [num_nodes, in_channels]
            edge_index: 边索引 [2, num_edges]
        """
        # 线性变换
        h = torch.mm(x, self.W)  # [num_nodes, out_channels * heads]
        h = h.view(-1, self.heads, self.out_channels)  # [num_nodes, heads, out_channels]
        
        # 添加自连接
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
        
        # 计算注意力权重并聚合
        h_prime = self.propagate(edge_index, x=h)
        
        if self.concat:
            return h_prime.view(-1, self.heads * self.out_channels)
        else:
            return h_prime.mean(dim=1)
    
    def message(self, x_i, x_j, edge_index_i):
        """消息函数：计算注意力权重和消息"""
        # x_i: 目标节点 [num_edges, heads, out_channels]
        # x_j: 源节点 [num_edges, heads, out_channels]
        
        # 计算注意力分数
        x_cat = torch.cat([x_i, x_j], dim=-1)  # [num_edges, heads, 2*out_channels]
        e = self.leaky_relu(torch.matmul(x_cat, self.a))  # [num_edges, heads, 1]
        e = e.squeeze(-1)  # [num_edges, heads]
        
        # Softmax 归一化
        alpha = F.softmax(e, dim=0)  # [num_edges, heads]
        alpha = F.dropout(alpha, p=self.dropout, training=self.training)
        
        # 加权消息
        return alpha.unsqueeze(-1) * x_j  # [num_edges, heads, out_channels]
    
    def aggregate(self, inputs, index, dim_size=None):
        """聚合函数：对邻居消息求和"""
        return torch.scatter_add(inputs, index, dim=0, dim_size=dim_size)

class GAT(nn.Module):
    """多层 GAT 模型"""
    
    def __init__(self, num_nodes, in_channels, hidden_channels, out_channels, 
                 num_layers=2, heads=8, dropout=0.6):
        super(GAT, self).__init__()
        self.num_layers = num_layers
        self.dropout = dropout
        
        self.layers = nn.ModuleList()
        self.layers.append(GATLayer(in_channels, hidden_channels, heads=heads, 
                                    dropout=dropout, concat=True))
        
        for _ in range(num_layers - 2):
            self.layers.append(GATLayer(hidden_channels * heads, hidden_channels, 
                                        heads=heads, dropout=dropout, concat=True))
        
        if num_layers > 1:
            self.layers.append(GATLayer(hidden_channels * heads, out_channels, 
                                       heads=heads, dropout=dropout, concat=False))
    
    def forward(self, x, edge_index):
        for i, layer in enumerate(self.layers):
            x = layer(x, edge_index)
            if i < len(self.layers) - 1:
                x = F.elu(x)
                x = F.dropout(x, p=self.dropout, training=self.training)
        return x

GraphSAGE

GraphSAGE（ Graph Sample and Aggregate）是一种归纳式（ Inductive）的 GNN 模型，能够为未见过的节点生成嵌入。

GraphSAGE 的核心思想：

与 GCN 不同， GraphSAGE 不要求所有节点在训练时都存在，它通过采样和聚合邻居来学习节点的表示。

采样策略：

GraphSAGE 使用固定大小的邻居采样： - 对于每个节点，随机采样 个邻居 - 逐层采样：第 层采样第 层节点的邻居

聚合函数：

GraphSAGE 支持多种聚合函数：

  1. 平均聚合（ Mean Aggregator）： Extra close brace or missing open brace\mathbf{h}_v^{(l+1)} = \sigma\left(\mathbf{W}^{(l)} \cdot \text{MEAN}\left(\{\mathbf{h}_v^{(l)}} \cup \{\mathbf{h}_u^{(l)} : u \in \mathcal{N}(v)} \right)\right)2. LSTM 聚合：使用 LSTM 处理邻居序列（需要固定顺序）

  2. 池化聚合（ Pooling Aggregator）： Extra close brace or missing open brace\mathbf{h}_v^{(l+1)} = \sigma\left(\mathbf{W}^{(l)} \cdot \text{CONCAT}\left(\mathbf{h}_v^{(l)}, \text{MAX}\left(\{\sigma(\mathbf{W}_{pool}\mathbf{h}_u^{(l)} + \mathbf{b}) : u \in \mathcal{N}(v)} \right)\right)\right)

GraphSAGE 实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch_geometric.nn import SAGEConv
from torch_geometric.data import Data, NeighborSampler

class GraphSAGE(nn.Module):
    """GraphSAGE 模型实现"""
    
    def __init__(self, in_channels, hidden_channels, out_channels, num_layers=2, dropout=0.5):
        super(GraphSAGE, self).__init__()
        self.num_layers = num_layers
        self.dropout = dropout
        
        self.convs = nn.ModuleList()
        self.convs.append(SAGEConv(in_channels, hidden_channels))
        
        for _ in range(num_layers - 2):
            self.convs.append(SAGEConv(hidden_channels, hidden_channels))
        
        if num_layers > 1:
            self.convs.append(SAGEConv(hidden_channels, out_channels))
    
    def forward(self, x, edge_index):
        for i, conv in enumerate(self.convs):
            x = conv(x, edge_index)
            if i < len(self.convs) - 1:
                x = F.relu(x)
                x = F.dropout(x, p=self.dropout, training=self.training)
        return x

# 使用 NeighborSampler 进行采样训练
def train_graphsage_with_sampling(model, data, train_loader, optimizer, device):
    """使用邻居采样训练 GraphSAGE"""
    model.train()
    total_loss = 0
    
    for batch_size, n_id, adjs in train_loader:
        # n_id: 当前 batch 涉及的所有节点 ID
        # adjs: 采样的邻接信息
        optimizer.zero_grad()
        
        # 获取节点特征
        x = data.x[n_id].to(device)
        
        # 逐层前向传播
        for i, (edge_index, _, size) in enumerate(adjs):
            edge_index = edge_index.to(device)
            x = model.convs[i](x, edge_index)
            if i < len(adjs) - 1:
                x = F.relu(x)
                x = F.dropout(x, p=model.dropout, training=model.training)
        
        # 计算损失（这里需要根据具体任务定义）
        # loss = compute_loss(...)
        # loss.backward()
        # optimizer.step()
        # total_loss += loss.item()
    
    return total_loss / len(train_loader)

推荐系统中的图建模

用户-物品二部图

推荐系统中最基本的图结构是用户-物品二部图（ User-Item Bipartite Graph）。

图定义：

  • 节点集合：，其中 是用户集合， 是物品集合
  • 边集合：
  • 边权重：可以是评分、点击次数、购买次数等

邻接矩阵：

用户-物品二部图的邻接矩阵可以表示为：

$$

A =

$$

其中 是用户-物品交互矩阵。

二部图的特点：

  1. 无三角形结构：用户节点之间没有直接连接，物品节点之间也没有直接连接
  2. 高阶关系：用户可以通过共同喜欢的物品建立间接关系，物品可以通过被相同用户喜欢建立间接关系
  3. 信息传播： GNN 可以在二部图上进行信息传播，学习用户和物品的表示

异构图建模

除了简单的二部图，推荐系统还可以构建更复杂的异构图（ Heterogeneous Graph）。

节点类型： - 用户节点 - 物品节点 - 属性节点（类别、标签、品牌等） - 上下文节点（时间、地点等）

边类型： - 用户-物品交互边（点击、购买、评分等） - 用户-用户社交边（关注、好友） - 物品-属性边（属于、包含） - 用户-属性边（偏好）

异构图示例：

1
2
3
用户 1 --[点击]--> 物品 A --[属于]--> 类别 1
用户 1 --[关注]--> 用户 2 --[购买]--> 物品 B
物品 A --[相似]--> 物品 C

图构建策略

基于交互的边： - 显式反馈：评分、评论 - 隐式反馈：点击、浏览、购买、收藏

边权重设计： - 二值权重：有交互为 1，无交互为 0 - 频率权重：交互次数 - 时间衰减权重： - 评分权重：直接使用评分值

负采样边： - 对于隐式反馈，需要采样负样本（用户未交互的物品） - 常用策略：随机负采样、基于流行度的负采样

PinSage： Pinterest 的大规模图推荐系统

PinSage 是 Pinterest 在 2018 年提出的用于大规模推荐系统的图神经网络模型，它能够处理包含 30 亿节点和 180 亿边的超大规模图。

PinSage 的核心设计

主要创新点：

  1. 重要性采样（ Importance-based Sampling）：不是随机采样邻居，而是根据重要性采样
  2. 卷积聚合：使用可学习的聚合函数
  3. 随机游走重要性：使用随机游走计算节点重要性
  4. 高效训练：支持大规模图的训练和推理

重要性采样

PinSage 使用随机游走计算节点的重要性分数：

对于节点 ，其重要性分数定义为从根节点 出发的随机游走访问 的次数：

$$

L(v) = _{t=1}^{T} P( u v t)$$

然后根据重要性分数采样 Top-K 邻居：

PinSage 聚合函数

PinSage 使用卷积聚合（ Convolve）来聚合邻居信息：

Extra close brace or missing open brace\mathbf{h}_v^{(l+1)} = \sigma\left(\mathbf{W}^{(l)} \cdot \text{CONCAT}\left[\mathbf{h}_v^{(l)}, \text{AGGREGATE}\left(\{\mathbf{h}_u^{(l)} : u \in \mathcal{N}(v)} \right)\right]\right)

其中 AGGREGATE 函数可以是： - 加权平均：根据重要性分数加权 - 最大池化：取最大值 - LSTM：使用 LSTM 处理邻居序列

PinSage 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from collections import defaultdict

class PinSageLayer(nn.Module):
    """PinSage 单层实现"""
    
    def __init__(self, in_channels, out_channels, num_samples=25, aggregator='mean'):
        super(PinSageLayer, self).__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.num_samples = num_samples
        self.aggregator = aggregator
        
        # 卷积层
        self.conv = nn.Linear(in_channels * 2, out_channels)
        
        # LSTM 聚合器（如果使用）
        if aggregator == 'lstm':
            self.lstm = nn.LSTM(in_channels, in_channels, batch_first=True)
    
    def forward(self, node_features, neighbors_list, importance_scores=None):
        """
        Args:
            node_features: 节点特征字典 {node_id: feature_vector}
            neighbors_list: 每个节点的邻居列表 {node_id: [neighbor_ids]}
            importance_scores: 重要性分数 {node_id: {neighbor_id: score }}
        """
        aggregated_features = {}
        
        for node_id, neighbors in neighbors_list.items():
            if len(neighbors) == 0:
                # 没有邻居，使用自身特征
                aggregated_features[node_id] = node_features[node_id]
                continue
            
            # 采样邻居
            if len(neighbors) > self.num_samples:
                if importance_scores and node_id in importance_scores:
                    # 根据重要性采样
                    neighbor_scores = [(n, importance_scores[node_id].get(n, 0)) 
                                      for n in neighbors]
                    neighbor_scores.sort(key=lambda x: x[1], reverse=True)
                    sampled_neighbors = [n for n, _ in neighbor_scores[:self.num_samples]]
                else:
                    # 随机采样
                    sampled_neighbors = np.random.choice(neighbors, 
                                                        self.num_samples, 
                                                        replace=False).tolist()
            else:
                sampled_neighbors = neighbors
            
            # 聚合邻居特征
            neighbor_features = [node_features[n] for n in sampled_neighbors]
            neighbor_features = torch.stack(neighbor_features)  # [num_neighbors, in_channels]
            
            if self.aggregator == 'mean':
                aggregated = neighbor_features.mean(dim=0)
            elif self.aggregator == 'max':
                aggregated = neighbor_features.max(dim=0)[0]
            elif self.aggregator == 'lstm':
                aggregated, _ = self.lstm(neighbor_features.unsqueeze(0))
                aggregated = aggregated[0, -1]  # 取最后一个时间步
            else:
                raise ValueError(f"Unknown aggregator: {self.aggregator}")
            
            # 拼接自身特征和聚合特征
            combined = torch.cat([node_features[node_id], aggregated], dim=-1)
            aggregated_features[node_id] = self.conv(combined)
        
        return aggregated_features

class PinSage(nn.Module):
    """PinSage 模型"""
    
    def __init__(self, num_nodes, in_channels, hidden_channels, out_channels, 
                 num_layers=2, num_samples=25, aggregator='mean'):
        super(PinSage, self).__init__()
        self.num_layers = num_layers
        
        self.layers = nn.ModuleList()
        self.layers.append(PinSageLayer(in_channels, hidden_channels, 
                                       num_samples, aggregator))
        
        for _ in range(num_layers - 2):
            self.layers.append(PinSageLayer(hidden_channels, hidden_channels, 
                                           num_samples, aggregator))
        
        if num_layers > 1:
            self.layers.append(PinSageLayer(hidden_channels, out_channels, 
                                           num_samples, aggregator))
    
    def forward(self, node_features, neighbors_list, importance_scores=None):
        x = node_features
        for layer in self.layers:
            x = layer(x, neighbors_list, importance_scores)
            x = {k: F.relu(v) for k, v in x.items()}
        return x

def compute_random_walk_importance(graph, root_node, num_walks=100, walk_length=5):
    """计算随机游走重要性分数"""
    importance = defaultdict(float)
    
    for _ in range(num_walks):
        current = root_node
        for step in range(walk_length):
            if current not in graph:
                break
            neighbors = graph[current]
            if len(neighbors) == 0:
                break
            
            # 随机选择下一个节点
            current = np.random.choice(neighbors)
            importance[current] += 1.0 / (step + 1)  # 距离越近，重要性越高
    
    return importance

PinSage 训练技巧

负采样： - 对于每个正样本 ，采样 个负样本 ，其中 是用户 未交互的物品 - 使用负采样损失： 硬负样本挖掘： - 不仅随机采样负样本，还采样"困难"的负样本（与用户历史交互物品相似的未交互物品） - 提高模型的区分能力

批量训练： - 使用 mini-batch 训练，每个 batch 包含多个用户及其邻居子图 - 使用图采样技术减少计算量

LightGCN：简化的图卷积推荐

LightGCN 是 2020 年提出的简化版图卷积推荐模型，它去除了 GCN 中的特征变换和非线性激活，只保留最核心的邻域聚合操作。

LightGCN 的设计理念

传统 GCN 的问题： - 特征变换（线性层）可能不适合推荐任务 - 非线性激活可能增加模型复杂度，但收益有限 - 自连接可能引入噪声

LightGCN 的简化： - 移除特征变换和非线性激活 - 移除自连接 - 只保留邻域聚合

LightGCN 的数学形式

LightGCN 的层更新公式：

其中： - 和 分别是用户和物品在第 层的嵌入 - 和 分别是用户和物品的邻居集合 - 归一化系数 是对称归一化

最终嵌入：

LightGCN 将各层的嵌入加权求和作为最终嵌入：

其中 是层权重，通常设置为 （均匀权重）。

预测分数：

用户 对物品 的预测分数：

LightGCN 实现

问题背景

传统的图神经网络方法（如 GCN 、 NGCF）在推荐系统中虽然有效，但存在一些问题：（ 1）模型复杂度高，包含特征变换、非线性激活等操作，训练和推理速度较慢；（ 2）对于推荐任务，这些复杂的操作可能不是必需的，甚至可能引入噪声；（ 3）在用户-物品二部图中，用户和物品的特征往往是 ID 嵌入，特征变换的作用有限。如何设计一个简单高效的 GNN 模型，既能捕获图结构信息，又能保持训练和推理的高效性，是推荐系统中的一个重要挑战。

解决思路

LightGCN（ Light Graph Convolutional Network）是专门为推荐系统设计的简化版 GCN 。基本思路：移除 GCN 中的特征变换和非线性激活，只保留最核心的邻域聚合操作。 LightGCN 认为，对于推荐任务，图结构信息比特征变换更重要，简单的邻域聚合就足以学习有效的节点表示。具体而言， LightGCN 的每一层只进行邻域聚合，然后将所有层的表示进行加权求和得到最终表示。这种设计大幅简化了模型，提升了训练和推理速度，同时在推荐任务上取得了更好的效果。

设计考虑

在实现 LightGCN 时，需要考虑以下几个关键设计：

  1. 简化的图卷积： LightGCN 移除了特征变换和非线性激活，每一层只进行邻域聚合。对于用户-物品二部图，用户节点的表示通过聚合其交互的物品节点得到，物品节点的表示通过聚合其交互的用户节点得到。这种设计使得模型更加轻量，训练和推理速度更快。

  2. 层组合策略： LightGCN 将所有层的表示进行加权求和得到最终表示，而不是只使用最后一层。这种设计能够同时利用不同层的信息：浅层捕获局部结构，深层捕获全局结构。通常使用均匀权重或可学习的权重，实验表明均匀权重效果已经很好。

  3. 嵌入初始化： LightGCN 使用随机初始化的嵌入，不需要预训练。嵌入维度通常设置为 64-256 维，根据用户和物品数量选择。

  4. 训练策略： LightGCN 使用 BPR 损失进行训练，最大化正样本（用户-物品交互）的得分，最小化负样本的得分。训练时使用负采样策略，每个正样本对应多个负样本。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from scipy.sparse import coo_matrix

class LightGCN(nn.Module):
    """LightGCN 模型实现"""
    
    def __init__(self, num_users, num_items, embedding_dim=64, num_layers=3):
        super(LightGCN, self).__init__()
        self.num_users = num_users
        self.num_items = num_items
        self.embedding_dim = embedding_dim
        self.num_layers = num_layers
        
        # 初始化嵌入
        self.user_embedding = nn.Embedding(num_users, embedding_dim)
        self.item_embedding = nn.Embedding(num_items, embedding_dim)
        
        # 初始化参数
        nn.init.normal_(self.user_embedding.weight, std=0.1)
        nn.init.normal_(self.item_embedding.weight, std=0.1)
        
        # 层权重（均匀权重）
        self.alpha = 1.0 / (num_layers + 1)
    
    def forward(self, user_indices, item_indices, graph):
        """
        Args:
            user_indices: 用户索引 [batch_size]
            item_indices: 物品索引 [batch_size]
            graph: 图结构（邻接矩阵或边索引）
        Returns:
            用户和物品的嵌入
        """
        # 获取初始嵌入
        user_emb = self.user_embedding.weight  # [num_users, embedding_dim]
        item_emb = self.item_embedding.weight  # [num_items, embedding_dim]
        
        # 存储各层嵌入
        user_embeddings = [user_emb]
        item_embeddings = [item_emb]
        
        # 逐层传播
        for _ in range(self.num_layers):
            # 用户嵌入更新：聚合邻居物品
            user_emb = self._propagate_users(user_emb, item_embeddings[-1], graph)
            user_embeddings.append(user_emb)
            
            # 物品嵌入更新：聚合邻居用户
            item_emb = self._propagate_items(item_emb, user_embeddings[-2], graph)
            item_embeddings.append(item_emb)
        
        # 加权求和
        final_user_emb = sum([self.alpha * emb for emb in user_embeddings])
        final_item_emb = sum([self.alpha * emb for emb in item_embeddings])
        
        # 获取 batch 对应的嵌入
        user_emb_batch = final_user_emb[user_indices]  # [batch_size, embedding_dim]
        item_emb_batch = final_item_emb[item_indices]  # [batch_size, embedding_dim]
        
        return user_emb_batch, item_emb_batch
    
    def _propagate_users(self, user_emb, item_emb, graph):
        """用户嵌入传播：聚合邻居物品"""
        # graph 是用户-物品交互矩阵 R
        # 归一化： 1 / sqrt(|N_u| * |N_i|)
        # 这里简化处理，实际需要根据图结构计算
        return user_emb  # 简化实现
    
    def _propagate_items(self, item_emb, user_emb, graph):
        """物品嵌入传播：聚合邻居用户"""
        return item_emb  # 简化实现
    
    def predict(self, user_indices, item_indices, graph):
        """预测用户对物品的评分"""
        user_emb, item_emb = self.forward(user_indices, item_indices, graph)
        scores = (user_emb * item_emb).sum(dim=1)
        return scores

class LightGCNWithSparseGraph(nn.Module):
    """使用稀疏矩阵的 LightGCN 实现"""
    
    def __init__(self, num_users, num_items, embedding_dim=64, num_layers=3):
        super(LightGCNWithSparseGraph, self).__init__()
        self.num_users = num_users
        self.num_items = num_items
        self.embedding_dim = embedding_dim
        self.num_layers = num_layers
        
        # 嵌入层
        self.user_embedding = nn.Embedding(num_users, embedding_dim)
        self.item_embedding = nn.Embedding(num_items, embedding_dim)
        
        nn.init.normal_(self.user_embedding.weight, std=0.1)
        nn.init.normal_(self.item_embedding.weight, std=0.1)
        
        self.alpha = 1.0 / (num_layers + 1)
    
    def build_graph(self, user_item_pairs):
        """构建归一化的图结构"""
        # user_item_pairs: [(user_id, item_id), ...]
        users, items = zip(*user_item_pairs)
        users = np.array(users)
        items = np.array(items)
        
        # 构建二部图邻接矩阵
        # [0, R]
        # [R^T, 0]
        num_nodes = self.num_users + self.num_items
        
        # 计算度
        user_degrees = np.bincount(users, minlength=self.num_users)
        item_degrees = np.bincount(items, minlength=self.num_items)
        
        # 构建归一化矩阵
        row = np.concatenate([users, items + self.num_users])
        col = np.concatenate([items + self.num_users, users])
        
        # 归一化权重
        norm = np.concatenate([
            1.0 / np.sqrt(user_degrees[users] * item_degrees[items]),
            1.0 / np.sqrt(user_degrees[users] * item_degrees[items])
        ])
        
        # 转换为稀疏矩阵
        from scipy.sparse import coo_matrix
        adj_matrix = coo_matrix((norm, (row, col)), shape=(num_nodes, num_nodes))
        
        return adj_matrix
    
    def forward(self, user_indices, item_indices, adj_matrix):
        """前向传播"""
        # 初始嵌入
        all_embeddings = torch.cat([
            self.user_embedding.weight,
            self.item_embedding.weight
        ], dim=0)  # [num_users + num_items, embedding_dim]
        
        embeddings_list = [all_embeddings]
        
        # 转换为 PyTorch 稀疏张量
        adj_tensor = self._sparse_matrix_to_tensor(adj_matrix).to(all_embeddings.device)
        
        # 逐层传播
        for _ in range(self.num_layers):
            all_embeddings = torch.sparse.mm(adj_tensor, all_embeddings)
            embeddings_list.append(all_embeddings)
        
        # 加权求和
        final_embeddings = sum([self.alpha * emb for emb in embeddings_list])
        
        # 分离用户和物品嵌入
        user_emb = final_embeddings[:self.num_users]
        item_emb = final_embeddings[self.num_users:]
        
        return user_emb[user_indices], item_emb[item_indices]
    
    def _sparse_matrix_to_tensor(self, sparse_matrix):
        """将 scipy 稀疏矩阵转换为 PyTorch 稀疏张量"""
        values = sparse_matrix.data
        indices = np.vstack((sparse_matrix.row, sparse_matrix.col))
        i = torch.LongTensor(indices)
        v = torch.FloatTensor(values)
        shape = sparse_matrix.shape
        return torch.sparse.FloatTensor(i, v, torch.Size(shape))

NGCF：神经图协同过滤

NGCF（ Neural Graph Collaborative Filtering）是 2019 年提出的将 GCN 应用于协同过滤的模型。

NGCF 的核心思想

NGCF 将用户-物品交互建模为二部图，使用 GCN 在图上进行信息传播，学习用户和物品的嵌入表示。

与传统矩阵分解的区别： - 矩阵分解只考虑直接交互 - NGCF 通过多层 GCN 捕捉高阶交互关系

NGCF 的数学形式

NGCF 的嵌入传播规则：

第一层传播：

第 层传播：

其中： - 表示逐元素相乘（元素级交互） - 和 是可学习的权重矩阵 - 是激活函数（如 LeakyReLU）

最终嵌入：

将各层嵌入拼接：

预测分数：

NGCF 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from scipy.sparse import coo_matrix

class NGCFLayer(nn.Module):
    """NGCF 单层实现"""
    
    def __init__(self, in_dim, out_dim, dropout=0.0):
        super(NGCFLayer, self).__init__()
        self.in_dim = in_dim
        self.out_dim = out_dim
        self.dropout = dropout
        
        # 权重矩阵
        self.W1 = nn.Linear(in_dim, out_dim, bias=False)
        self.W2 = nn.Linear(in_dim, out_dim, bias=False)
        
        self.reset_parameters()
    
    def reset_parameters(self):
        nn.init.xavier_uniform_(self.W1.weight)
        nn.init.xavier_uniform_(self.W2.weight)
    
    def forward(self, user_emb, item_emb, user_item_graph, item_user_graph):
        """
        Args:
            user_emb: 用户嵌入 [num_users, in_dim]
            item_emb: 物品嵌入 [num_items, in_dim]
            user_item_graph: 用户-物品图（稀疏矩阵）
            item_user_graph: 物品-用户图（稀疏矩阵）
        """
        # 用户嵌入传播
        # 1. 自连接
        user_emb_self = self.W1(user_emb)
        
        # 2. 从物品聚合
        item_to_user = torch.sparse.mm(user_item_graph, item_emb)  # [num_users, in_dim]
        item_to_user = self.W1(item_to_user)
        
        # 3. 元素级交互
        user_item_interaction = torch.sparse.mm(user_item_graph, 
                                                item_emb * user_emb)  # [num_users, in_dim]
        user_item_interaction = self.W2(user_item_interaction)
        
        # 4. 聚合
        user_emb_new = user_emb_self + item_to_user + user_item_interaction
        user_emb_new = F.leaky_relu(user_emb_new, negative_slope=0.2)
        user_emb_new = F.dropout(user_emb_new, p=self.dropout, training=self.training)
        
        # 物品嵌入传播（类似）
        item_emb_self = self.W1(item_emb)
        user_to_item = torch.sparse.mm(item_user_graph, user_emb)
        user_to_item = self.W1(user_to_item)
        item_user_interaction = torch.sparse.mm(item_user_graph, 
                                                user_emb * item_emb)
        item_user_interaction = self.W2(item_user_interaction)
        
        item_emb_new = item_emb_self + user_to_item + item_user_interaction
        item_emb_new = F.leaky_relu(item_emb_new, negative_slope=0.2)
        item_emb_new = F.dropout(item_emb_new, p=self.dropout, training=self.training)
        
        return user_emb_new, item_emb_new

class NGCF(nn.Module):
    """NGCF 模型"""
    
    def __init__(self, num_users, num_items, embedding_dim=64, num_layers=3, dropout=0.1):
        super(NGCF, self).__init__()
        self.num_users = num_users
        self.num_items = num_items
        self.embedding_dim = embedding_dim
        self.num_layers = num_layers
        
        # 初始嵌入
        self.user_embedding = nn.Embedding(num_users, embedding_dim)
        self.item_embedding = nn.Embedding(num_items, embedding_dim)
        
        nn.init.normal_(self.user_embedding.weight, std=0.1)
        nn.init.normal_(self.item_embedding.weight, std=0.1)
        
        # NGCF 层
        self.layers = nn.ModuleList()
        for i in range(num_layers):
            self.layers.append(NGCFLayer(embedding_dim, embedding_dim, dropout))
    
    def build_graph(self, user_item_pairs):
        """构建图结构"""
        users, items = zip(*user_item_pairs)
        users = np.array(users)
        items = np.array(items)
        
        # 计算归一化系数
        user_degrees = np.bincount(users, minlength=self.num_users)
        item_degrees = np.bincount(items, minlength=self.num_items)
        
        # 用户-物品图
        norm_user_item = 1.0 / np.sqrt(user_degrees[users] * item_degrees[items])
        user_item_graph = coo_matrix(
            (norm_user_item, (users, items)),
            shape=(self.num_users, self.num_items)
        )
        
        # 物品-用户图（转置）
        item_user_graph = user_item_graph.T
        
        return user_item_graph, item_user_graph
    
    def forward(self, user_indices, item_indices, user_item_graph, item_user_graph):
        """前向传播"""
        # 初始嵌入
        user_emb = self.user_embedding.weight
        item_emb = self.item_embedding.weight
        
        # 存储各层嵌入
        user_embeddings = [user_emb]
        item_embeddings = [item_emb]
        
        # 转换为 PyTorch 稀疏张量
        user_item_tensor = self._sparse_matrix_to_tensor(user_item_graph).to(user_emb.device)
        item_user_tensor = self._sparse_matrix_to_tensor(item_user_graph).to(item_emb.device)
        
        # 逐层传播
        for layer in self.layers:
            user_emb, item_emb = layer(user_emb, item_emb, user_item_tensor, item_user_tensor)
            user_embeddings.append(user_emb)
            item_embeddings.append(item_emb)
        
        # 拼接各层嵌入
        final_user_emb = torch.cat(user_embeddings, dim=1)  # [num_users, embedding_dim * (num_layers+1)]
        final_item_emb = torch.cat(item_embeddings, dim=1)  # [num_items, embedding_dim * (num_layers+1)]
        
        return final_user_emb[user_indices], final_item_emb[item_indices]
    
    def predict(self, user_indices, item_indices, user_item_graph, item_user_graph):
        """预测评分"""
        user_emb, item_emb = self.forward(user_indices, item_indices, 
                                         user_item_graph, item_user_graph)
        scores = (user_emb * item_emb).sum(dim=1)
        return scores
    
    def _sparse_matrix_to_tensor(self, sparse_matrix):
        """转换为 PyTorch 稀疏张量"""
        values = sparse_matrix.data
        indices = np.vstack((sparse_matrix.row, sparse_matrix.col))
        i = torch.LongTensor(indices)
        v = torch.FloatTensor(values)
        shape = sparse_matrix.shape
        return torch.sparse.FloatTensor(i, v, torch.Size(shape))

社交推荐系统

社交推荐（ Social Recommendation）利用用户之间的社交关系来提升推荐效果。

社交推荐的基本思想

核心假设： - 用户倾向于喜欢其社交好友喜欢的物品 - 社交关系可以提供额外的信号来缓解数据稀疏性问题 - 社交影响力会影响用户的决策

社交图的构建

社交关系类型： - 显式关系：关注、好友、粉丝 - 隐式关系：共同兴趣、相似行为

社交图表示： - 无向图：好友关系 - 有向图：关注关系 - 加权图：关系强度

社交推荐模型

SoRec（ Social Recommendation）： 结合用户-物品交互和用户-用户社交关系：

其中 是从社交关系学习到的用户表示。

SocialMF： 使用矩阵分解同时建模交互和社交关系：

其中 是用户 的社交好友集合。

GraphRec（ Graph Neural Network for Social Recommendation）： 使用 GNN 同时建模用户-物品交互和用户-用户社交关系。

GraphRec 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import torch
import torch.nn as nn
import torch.nn.functional as F

class GraphRec(nn.Module):
    """GraphRec: 社交推荐模型"""
    
    def __init__(self, num_users, num_items, embedding_dim=64, 
                 social_graph=None, num_layers=2):
        super(GraphRec, self).__init__()
        self.num_users = num_users
        self.num_items = num_items
        self.embedding_dim = embedding_dim
        
        # 用户和物品嵌入
        self.user_embedding = nn.Embedding(num_users, embedding_dim)
        self.item_embedding = nn.Embedding(num_items, embedding_dim)
        
        # 社交关系嵌入（可选）
        if social_graph is not None:
            self.social_embedding = nn.Embedding(num_users, embedding_dim)
        
        # GNN 层
        self.gnn_layers = nn.ModuleList()
        for _ in range(num_layers):
            self.gnn_layers.append(SocialGNNLayer(embedding_dim))
    
    def forward(self, user_indices, item_indices, user_item_graph, social_graph):
        """前向传播"""
        # 初始嵌入
        user_emb = self.user_embedding.weight
        item_emb = self.item_embedding.weight
        
        # 社交信息传播
        for layer in self.gnn_layers:
            user_emb = layer(user_emb, social_graph)
        
        # 交互信息传播
        # ...（类似 NGCF 的传播过程）
        
        return user_emb[user_indices], item_emb[item_indices]

class SocialGNNLayer(nn.Module):
    """社交 GNN 层"""
    
    def __init__(self, embedding_dim):
        super(SocialGNNLayer, self).__init__()
        self.embedding_dim = embedding_dim
        self.linear = nn.Linear(embedding_dim, embedding_dim)
    
    def forward(self, user_emb, social_graph):
        """在社交图上传播"""
        # social_graph: 稀疏矩阵 [num_users, num_users]
        # 聚合社交邻居
        social_emb = torch.sparse.mm(social_graph, user_emb)
        # 更新
        updated_emb = self.linear(user_emb + social_emb)
        return F.relu(updated_emb)

图采样与训练技巧

图采样策略

邻居采样（ Neighbor Sampling）： - 固定大小采样：每个节点采样固定数量的邻居 - 重要性采样：根据重要性分数采样 - 随机采样：随机选择邻居

子图采样（ Subgraph Sampling）： - 随机游走采样：从根节点开始随机游走，采样子图 - 广度优先采样： BFS 采样固定跳数的子图 - 层采样：逐层采样邻居

负采样策略

随机负采样： - 为每个正样本随机选择负样本 - 简单但可能不够困难

基于流行度的负采样： - 更倾向于采样热门物品作为负样本 - 假设用户更可能知道热门物品但未交互

硬负样本挖掘： - 采样与用户历史交互物品相似的未交互物品 - 提高模型的区分能力

训练技巧

批量训练： - 使用 mini-batch 训练 - 每个 batch 包含多个用户及其子图

学习率调度： - 使用学习率衰减 - 预热（ Warm-up）策略

正则化： - L2 正则化 - Dropout - 嵌入归一化

优化器选择： - Adam 、 AdamW - 学习率：通常 0.001-0.01

完整代码实现示例

数据准备

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from scipy.sparse import coo_matrix

class RecommendationDataset:
    """推荐系统数据集"""
    
    def __init__(self, data_path, test_size=0.2):
        # 加载数据
        self.df = pd.read_csv(data_path)
        # 假设数据格式： user_id, item_id, rating, timestamp
        
        # 编码用户和物品 ID
        self.user_encoder = {uid: idx for idx, uid in enumerate(self.df['user_id'].unique())}
        self.item_encoder = {iid: idx for idx, iid in enumerate(self.df['item_id'].unique())}
        self.user_decoder = {idx: uid for uid, idx in self.user_encoder.items()}
        self.item_decoder = {idx: iid for iid, idx in self.item_encoder.items()}
        
        self.num_users = len(self.user_encoder)
        self.num_items = len(self.item_encoder)
        
        # 编码数据
        self.df['user_idx'] = self.df['user_id'].map(self.user_encoder)
        self.df['item_idx'] = self.df['item_id'].map(self.item_encoder)
        
        # 划分训练集和测试集
        self.train_df, self.test_df = train_test_split(
            self.df, test_size=test_size, random_state=42
        )
        
        # 构建交互矩阵
        self.train_matrix = self._build_matrix(self.train_df)
        self.test_matrix = self._build_matrix(self.test_df)
    
    def _build_matrix(self, df):
        """构建用户-物品交互矩阵"""
        row = df['user_idx'].values
        col = df['item_idx'].values
        data = np.ones(len(df))
        return coo_matrix((data, (row, col)), 
                         shape=(self.num_users, self.num_items))
    
    def get_user_item_pairs(self, df=None):
        """获取用户-物品对"""
        if df is None:
            df = self.train_df
        return list(zip(df['user_idx'].values, df['item_idx'].values))

训练循环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
import torch
import torch.optim as optim
from torch.utils.data import DataLoader, Dataset

class BPRDataset(Dataset):
    """BPR 损失的数据集"""
    
    def __init__(self, user_item_pairs, num_items, num_negatives=1):
        self.user_item_pairs = user_item_pairs
        self.num_items = num_items
        self.num_negatives = num_negatives
        
        # 构建用户交互集合（用于负采样）
        self.user_items = {}
        for u, i in user_item_pairs:
            if u not in self.user_items:
                self.user_items[u] = set()
            self.user_items[u].add(i)
    
    def __len__(self):
        return len(self.user_item_pairs) * (1 + self.num_negatives)
    
    def __getitem__(self, idx):
        pos_idx = idx // (1 + self.num_negatives)
        u, i_pos = self.user_item_pairs[pos_idx]
        
        # 负采样
        i_neg = np.random.randint(0, self.num_items)
        while i_neg in self.user_items.get(u, set()):
            i_neg = np.random.randint(0, self.num_items)
        
        return u, i_pos, i_neg

def bpr_loss(user_emb, item_pos_emb, item_neg_emb):
    """BPR 损失函数"""
    pos_scores = (user_emb * item_pos_emb).sum(dim=1)
    neg_scores = (user_emb * item_neg_emb).sum(dim=1)
    loss = -torch.log(torch.sigmoid(pos_scores - neg_scores) + 1e-10).mean()
    return loss

def train_lightgcn(model, dataset, num_epochs=100, batch_size=1024, 
                   lr=0.001, device='cuda'):
    """训练 LightGCN 模型"""
    # 构建图
    user_item_pairs = dataset.get_user_item_pairs()
    user_item_graph, item_user_graph = model.build_graph(user_item_pairs)
    
    # 数据集和数据加载器
    train_dataset = BPRDataset(user_item_pairs, dataset.num_items)
    train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
    
    # 优化器
    optimizer = optim.Adam(model.parameters(), lr=lr)
    
    model = model.to(device)
    user_item_graph = user_item_graph.to(device)
    item_user_graph = item_user_graph.to(device)
    
    # 训练循环
    for epoch in range(num_epochs):
        model.train()
        total_loss = 0
        
        for batch_users, batch_items_pos, batch_items_neg in train_loader:
            batch_users = batch_users.to(device)
            batch_items_pos = batch_items_pos.to(device)
            batch_items_neg = batch_items_neg.to(device)
            
            optimizer.zero_grad()
            
            # 前向传播
            user_emb_pos, item_emb_pos = model(batch_users, batch_items_pos, 
                                               user_item_graph, item_user_graph)
            user_emb_neg, item_emb_neg = model(batch_users, batch_items_neg, 
                                               user_item_graph, item_user_graph)
            
            # 计算损失
            loss = bpr_loss(user_emb_pos, item_emb_pos, item_emb_neg)
            
            # 反向传播
            loss.backward()
            optimizer.step()
            
            total_loss += loss.item()
        
        avg_loss = total_loss / len(train_loader)
        print(f"Epoch {epoch+1}/{num_epochs}, Loss: {avg_loss:.4f}")
        
        # 评估
        if (epoch + 1) % 10 == 0:
            evaluate(model, dataset, user_item_graph, item_user_graph, device)

def evaluate(model, dataset, user_item_graph, item_user_graph, device, k=10):
    """评估模型"""
    model.eval()
    
    # 获取所有用户和物品的嵌入
    all_users = torch.arange(dataset.num_users).to(device)
    all_items = torch.arange(dataset.num_items).to(device)
    
    with torch.no_grad():
        user_emb, item_emb = model(all_users, all_items, 
                                   user_item_graph, item_user_graph)
        
        # 计算所有用户-物品对的分数
        scores = torch.matmul(user_emb, item_emb.T)  # [num_users, num_items]
        
        # 计算 HR@K 和 NDCG@K
        hr_sum = 0
        ndcg_sum = 0
        
        for u in range(dataset.num_users):
            # 获取测试集中的正样本
            test_items = dataset.test_matrix[u].nonzero()[1]
            if len(test_items) == 0:
                continue
            
            # 获取预测分数
            u_scores = scores[u].cpu().numpy()
            
            # 排除训练集中的物品
            train_items = dataset.train_matrix[u].nonzero()[1]
            u_scores[train_items] = -np.inf
            
            # Top-K 推荐
            top_k_items = np.argsort(u_scores)[-k:][::-1]
            
            # 计算 HR@K
            hr = len(set(top_k_items) & set(test_items)) / len(test_items)
            hr_sum += hr
            
            # 计算 NDCG@K
            dcg = 0
            for i, item in enumerate(top_k_items):
                if item in test_items:
                    dcg += 1 / np.log2(i + 2)
            idcg = sum([1 / np.log2(i + 2) for i in range(min(k, len(test_items)))])
            ndcg = dcg / idcg if idcg > 0 else 0
            ndcg_sum += ndcg
        
        avg_hr = hr_sum / dataset.num_users
        avg_ndcg = ndcg_sum / dataset.num_users
        
        print(f"HR@{k}: {avg_hr:.4f}, NDCG@{k}: {avg_ndcg:.4f}")

总结

图神经网络为推荐系统带来了新的可能性，它能够直接建模用户和物品之间的复杂关系，捕捉高阶交互模式。从基础的 GCN 、 GAT 、 GraphSAGE，到推荐场景中的 PinSage 、 LightGCN 、 NGCF，再到社交推荐， GNN 在推荐领域展现出了强大的能力。

关键要点：

  1. 图建模：将推荐问题转化为图上的表示学习问题
  2. 信息传播：通过多层 GNN 捕捉高阶关系
  3. 简化设计： LightGCN 证明了简化设计的有效性
  4. 社交信息：利用社交关系提升推荐效果
  5. 采样技巧：使用采样技术处理大规模图

未来方向：

  • 动态图推荐：建模时间演化的图结构
  • 异构图推荐：处理多种类型的节点和边
  • 可解释性：提高模型的可解释性
  • 效率优化：进一步提升大规模图的训练和推理效率

❓ Q&A: 图神经网络推荐常见问题

GNN 相比传统矩阵分解有什么优势？

GNN 能够捕捉用户和物品之间的高阶关系。矩阵分解只考虑直接交互，而 GNN 通过多层传播可以捕捉"用户 A 喜欢物品 X，用户 B 也喜欢物品 X，用户 B 还喜欢物品 Y，因此用户 A 可能也喜欢物品 Y"这样的高阶关系。

LightGCN 为什么去掉特征变换和非线性激活？

LightGCN 的作者通过实验发现，在推荐任务中，特征变换和非线性激活带来的收益有限，反而增加了模型复杂度。去掉这些组件后，模型更简单，训练更快，效果反而更好。这说明推荐任务可能不需要太复杂的特征变换。

如何处理大规模图的训练？

主要方法包括： 1. 图采样：采样子图或邻居进行训练 2. 批量训练：使用 mini-batch 训练 3. 分布式训练：将图分割到多个设备 4. 近似方法：使用近似算法减少计算量

PinSage 的重要性采样是如何工作的？

PinSage 使用随机游走计算节点的重要性分数。从根节点出发进行多次随机游走，统计每个节点被访问的次数和距离，距离越近、访问次数越多的节点重要性越高。然后根据重要性分数采样 Top-K 邻居，而不是随机采样。

NGCF 中的元素级交互（ element-wise product）有什么作用？

元素级交互 能够捕捉用户和物品之间的细粒度交互模式，类似于协同过滤中的"用户-物品对"特征。这种交互可以帮助模型学习到更丰富的表示。

社交推荐一定比非社交推荐好吗？

不一定。社交推荐的效果取决于： 1. 社交关系的质量：如果社交关系与兴趣相关性低，可能没有帮助 2. 数据稀疏性：在数据非常稀疏时，社交信息可能更有用 3. 领域特性：某些领域（如音乐、电影）社交影响更大

如何选择 GNN 的层数？

通常 2-3 层就足够了。层数过多可能导致： 1. 过平滑：所有节点的表示变得相似 2. 过拟合：模型复杂度增加 3. 计算成本：训练和推理时间增加

可以通过实验选择最优层数，通常从 2 层开始尝试。

图采样会影响模型效果吗？

合理的采样策略通常不会显著影响效果，反而可能带来以下好处： 1. 防止过拟合：采样相当于一种正则化 2. 提高效率：减少计算量 3. 增加多样性：不同 epoch 采样不同的子图

但采样策略需要仔细设计，确保采样的邻居具有代表性。

如何处理冷启动问题？

GNN 可以通过以下方式缓解冷启动： 1. 利用图结构：新用户/物品可以通过邻居节点获得初始表示 2. 内容特征：结合内容特征初始化嵌入 3. 迁移学习：从其他领域迁移知识

BPR 损失和交叉熵损失有什么区别？

BPR（ Bayesian Personalized Ranking）损失是成对损失，它比较正样本和负样本的分数差，目标是让正样本分数高于负样本。交叉熵损失是点对损失，直接预测用户对物品的偏好概率。 BPR 更适合隐式反馈场景，因为它不需要显式的评分标签。

如何评估图推荐模型？

主要指标包括： 1. 准确率指标： HR@K 、 NDCG@K 、 MRR 2. 覆盖率：推荐物品的多样性 3. 新颖性：推荐长尾物品的能力 4. 效率指标：训练时间、推理时间

GNN 推荐模型可以处理动态图吗？

可以，但需要特殊设计： 1. 时间编码：在节点/边特征中加入时间信息 2. 时间采样：只采样特定时间窗口内的边 3. 动态 GNN：使用专门处理动态图的模型（如 EvolveGCN 、 TGN）

图推荐模型的可解释性如何？

GNN 的可解释性可以通过以下方式提升： 1. 注意力权重： GAT 的注意力权重可以解释哪些邻居更重要 2. 路径解释：解释信息传播的路径 3. 可视化：可视化节点嵌入和关系

如何处理异构图推荐？

异构图推荐需要： 1. 类型编码：为不同类型的节点和边使用不同的编码 2. 元路径：定义有意义的元路径（如"用户-物品-用户"） 3. 异构图 GNN：使用专门处理异构图的模型（如 HAN 、 HetGNN）

  • 本文标题：推荐系统（七）—— 图神经网络与社交推荐
  • 本文作者：Chen Kai
  • 创建时间：2024-06-01 10:30:00
  • 本文链接：https://www.chenk.top/%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%EF%BC%88%E4%B8%83%EF%BC%89%E2%80%94%E2%80%94-%E5%9B%BE%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%E4%B8%8E%E7%A4%BE%E4%BA%A4%E6%8E%A8%E8%8D%90/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
 评论