推荐系统已经渗透到我们数字生活的每个角落。打开淘宝,首页的商品推荐;刷抖音,算法推送的视频;听网易云音乐,每日推荐歌单;甚至打开知乎,首页的问题推荐——这些背后都有一套复杂的推荐系统在运作。
但推荐系统到底是什么?它如何知道我们可能喜欢什么?为什么有时候推荐得很准,有时候又让人摸不着头脑?本文将从零开始,带你理解推荐系统的核心概念、主流方法、评估指标、系统架构,以及实现细节。我们会用代码和例子说话,而不是停留在理论层面。
什么是推荐系统
推荐系统( Recommendation
System)是一类信息过滤系统,它的目标是在信息过载的时代,帮助用户从海量候选项中快速找到感兴趣的内容。用更技术化的语言说,推荐系统要解决的核心问题是:给定用户
。
推荐系统的价值
推荐系统之所以重要,是因为它解决了三个核心问题:
信息过载 :互联网上的信息量呈指数级增长。 YouTube
每分钟上传超过 500 小时的视频,淘宝有数亿商品, Netflix
有数万部电影。用户不可能浏览所有内容,需要有人帮他们筛选。
长尾效应 :在电商、内容平台中,少数热门商品/内容占据了大部分流量,而大量小众商品/内容很难被用户发现。推荐系统能够挖掘长尾内容,提高整体生态的多样性。
商业价值 :好的推荐系统能显著提升用户体验和平台指标。
Netflix 声称其推荐系统贡献了 80% 的观看量; Amazon 的推荐系统贡献了 35%
的收入; YouTube 的推荐系统让用户观看时长提升了 50% 以上。
推荐系统的应用场景
推荐系统几乎无处不在:
电商平台 :商品推荐、相关商品、猜你喜欢内容平台 :新闻推荐、视频推荐、文章推荐社交网络 :好友推荐、内容推荐音乐/视频平台 :歌单推荐、视频推荐广告系统 :个性化广告投放招聘平台 :职位推荐、候选人推荐
推荐系统的历史发展
推荐系统的发展可以追溯到 20 世纪 90 年代:
1990s - 起步阶段 : - 1992 年, Xerox PARC 的
Tapestry 系统首次提出"协同过滤"概念 - 1994 年, GroupLens
系统使用协同过滤推荐新闻 - 1997 年, Amazon 开始使用推荐系统
2000s - 成熟阶段 : - 2003 年, Netflix Prize
竞赛推动了矩阵分解等算法的发展 - 2006 年, YouTube 推出推荐系统 - 2009
年, Netflix Prize 结束,矩阵分解成为主流方法
2010s - 深度学习时代 : - 2016 年, Google 提出
Wide&Deep 模型 - 2017 年,华为提出 DeepFM 模型 - 2018
年,阿里巴巴提出 DIN( Deep Interest Network)模型
2020s - 序列推荐和强化学习 : - Transformer
架构在推荐系统中的应用 - 强化学习在推荐系统中的应用 -
多模态推荐系统的发展
推荐系统的三大范式
推荐系统的主流方法可以归纳为三大范式:协同过滤 (
Collaborative Filtering)、内容推荐 ( Content-Based
Recommendation)和混合推荐 ( Hybrid
Recommendation)。
协同过滤( Collaborative
Filtering)
协同过滤的基本思路:相似的用户会有相似的偏好,相似的物品会被相似的用户喜欢 。它不需要知道物品的内容特征,只需要用户的历史行为数据(评分、点击、购买等)。
协同过滤分为两类:
基于用户的协同过滤(
User-CF) :找到与目标用户相似的用户,推荐这些相似用户喜欢但目标用户还没接触过的物品。
基于物品的协同过滤(
Item-CF) :找到与用户历史喜欢的物品相似的物品,推荐给用户。
User-CF 算法详解
User-CF 的流程如下:
构建用户-物品评分矩阵 :矩阵
计算用户相似度 :使用余弦相似度、皮尔逊相关系数等方法计算用户之间的相似度。
预测评分 :对于用户
生成推荐 :对预测评分排序,取 Top-N
推荐。
用户相似度的计算有多种方法:
余弦相似度 :
直观理解(用考试成绩类比)
想象两个学生的成绩单: -
小王 :语文90分,数学85分,英语70分 -
小李 :语文85分,数学80分,英语65分
他们的成绩"相似"吗?
相似度的本质 :看两人各科成绩的"同步程度" -
如果小王某科高分,小李这科也高分 → 相似度高 -
如果小王高分的科目,小李全是低分 → 相似度低
余弦相似度的计算 : 1.
把成绩单看作向量:小王=[90,85,70],小李=[85,80,65] 2.
计算"对应项相乘再相加":90×85 + 85×80 + 70×65 3.
除以两人各自的"总体水平"(归一化)
数学公式 : $$
sim(u, v) = { } $$
符号解释 : -
结果范围 :-1到1之间 - 1:完全相似(成绩完全同步) -
0:无关(没有相关性) - -1:完全相反(一个高分,另一个低分)
皮尔逊相关系数 : $$
sim(u, v) = $$
其中
预测评分的公式:
其中
Item-CF 算法详解
Item-CF 的流程与 User-CF 类似,但是基于物品相似度:
构建用户-物品评分矩阵 计算物品相似度 :计算物品之间的相似度预测评分 :对于用户 生成推荐 :对预测评分排序,取 Top-N
物品相似度计算: $$
sim(i, j) = { } $$
其中
预测评分:
其中
User-CF vs Item-CF
两种方法各有优劣:
User-CF 适合 : - 用户数量相对较少 -
物品数量多且更新频繁 - 用户兴趣变化快
Item-CF 适合 : - 物品数量相对较少 - 用户数量多 -
物品内容相对稳定
在实际应用中, Item-CF 更常用,因为: 1. 物品相似度比用户相似度更稳定
2. 物品数量通常少于用户数量,计算效率更高 3. 可解释性更好("因为你喜欢
A,所以推荐相似的 B")
内容推荐( Content-Based
Recommendation)
内容推荐的基本思路:分析用户历史喜欢的物品特征,推荐具有相似特征的物品 。它需要知道物品的内容特征(文本、标签、类别等)。
内容推荐的流程:
物品特征提取 :从物品内容中提取特征向量(如 TF-IDF
、词向量等)用户画像构建 :基于用户历史行为,构建用户偏好向量相似度计算 :计算候选物品与用户画像的相似度生成推荐 :按相似度排序,取 Top-N
用户画像通常用用户历史喜欢物品的特征向量加权平均: $$
profile_u = $$
其中
混合推荐( Hybrid
Recommendation)
混合推荐结合多种推荐方法,取长补短。常见的混合策略:
加权混合 :将不同方法的预测分数加权平均
切换混合 :根据场景选择不同的方法
特征混合 :将协同过滤和内容推荐的特征合并,训练统一模型
级联混合 :先用一种方法生成候选,再用另一种方法排序
元级混合 :训练一个元模型,学习如何组合不同方法的输出
协同过滤的数学原理
为了更好地理解协同过滤,需要深入其数学原理。
矩阵表示
用户-物品评分矩阵可以表示为
由于数据稀疏性,矩阵
相似度度量的选择
不同的相似度度量适用于不同的场景:
余弦相似度 :适合处理评分尺度不同的情况,因为它只考虑方向而不考虑大小。
皮尔逊相关系数 :考虑了用户评分习惯的差异(有些用户倾向于打高分,有些倾向于打低分),通过减去平均评分来消除这种偏差。
调整余弦相似度 :在 Item-CF
中,减去用户平均评分可以消除用户评分习惯的影响。
Jaccard
相似度 :适用于隐式反馈(只有喜欢/不喜欢,没有评分),计算两个集合的交集与并集的比值。
相似度计算的优化
在实际应用中,计算所有用户对或物品对的相似度计算量很大。优化方法:
稀疏矩阵优化 :只计算有共同评分的用户对/物品对采样 :随机采样部分用户/物品计算相似度LSH( Locality Sensitive
Hashing) :使用哈希函数快速找到相似用户/物品分布式计算 :使用 MapReduce 等框架并行计算
内容推荐的深入理解
内容推荐的核心是特征提取和相似度计算。
文本特征提取
对于文本内容,常用的特征提取方法:
TF-IDF :词频-逆文档频率,衡量词语的重要性 $$
TFIDF(t, d) = TF(t, d) IDF(t)$$
其中
Word2Vec /
Doc2Vec :将词语或文档映射到低维向量空间,语义相似的词语/文档在向量空间中距离较近。
BERT :使用预训练的 BERT
模型提取文本的深层语义特征。
图像特征提取
对于图像内容,可以使用:
CNN 特征 :使用预训练的 CNN(如 ResNet 、
VGG)提取图像特征多模态模型 :结合文本和图像特征
用户画像的构建
用户画像是对用户兴趣的抽象表示,可以通过以下方式构建:
加权平均 :用户历史喜欢物品的特征向量加权平均时间衰减 :给最近的行为更高权重 $$
profile_u = $$
其中
聚类 :将用户聚类,使用聚类中心作为用户画像
混合推荐的策略选择
不同混合策略适用于不同场景:
加权混合 :适合不同方法效果相近的情况,权重可以通过验证集调优。
切换混合 :适合不同方法在不同场景下表现差异大的情况。例如,新用户用内容推荐,老用户用协同过滤。
特征混合 :适合有丰富特征的情况,可以训练端到端的深度学习模型。
级联混合 :适合计算资源有限的情况,先用简单方法召回,再用复杂方法排序。
元级混合 :适合有多种推荐方法且效果差异大的情况,但需要额外的训练数据。
推荐系统评估指标
评估推荐系统的质量需要从多个维度考虑。没有单一指标能全面反映推荐系统的效果,需要组合使用多个指标。
准确率指标
准确率( Precision)和召回率(
Recall)
准确率衡量推荐结果中有多少是用户真正喜欢的: $$
Precision@K = $$
召回率衡量用户真正喜欢的物品中有多少被推荐了: $$
Recall@K = $$
其中
准确率和召回率通常存在权衡:提高召回率可能会降低准确率,反之亦然。可以用
F1 分数综合两者: $$
F1@K = $$
平均准确率( Mean Average
Precision, MAP)
MAP 考虑了推荐列表中的位置信息,位置越靠前的正确推荐权重越大: $$
AP(u) = _{k=1}^{K} Precision@k rel(k)$$
其中
$$
MAP = _{u U} AP(u)$$
NDCG( Normalized
Discounted Cumulative Gain)
NDCG
是信息检索中常用的指标,也适用于推荐系统。它考虑了位置折扣和相关性等级:
$$
DCG@K = _{i=1}^{K} $$
其中
$$
NDCG@K = $$
其中
多样性指标
多样性衡量推荐结果的丰富程度,避免推荐过于同质化。
类别多样性 :推荐列表中不同类别的数量 $$
Diversity = $$
平均成对距离 :推荐物品之间的平均距离 $$
Intra-List Diversity = {i R(u)} {j R(u), j i} distance(i,
j)$$
覆盖率指标
覆盖率衡量推荐系统能够推荐多少不同的物品。
物品覆盖率 :被推荐过的物品占总物品的比例 $$
Coverage = $$
长尾覆盖率 :推荐列表中长尾物品的比例
新颖性指标
新颖性衡量推荐物品的新鲜程度,避免总是推荐热门物品。
平均流行度倒数 : $$
Novelty = _{i R(u)} $$
实时性指标
对于新闻、短视频等时效性强的场景,还需要考虑实时性: -
推荐内容的新鲜度(发布时间) - 系统响应时间 - 更新频率
评估指标的实践建议
在实际应用中,评估指标的选择需要考虑:
业务目标 :如果目标是提升点击率,重点关注
Precision 和 Recall;如果目标是提升多样性,重点关注 Diversity 和
Coverage 。
数据特点 :对于显式反馈(评分),可以使用
Precision 、 Recall 、 NDCG;对于隐式反馈(点击),更适合使用 Precision
、 Recall 、 MAP 。
离线 vs 在线 :离线指标( Precision 、 Recall
等)和在线指标( CTR 、 GMV 等)可能不一致,需要通过 A/B
测试验证。
多指标组合 :不要只看单一指标,要综合考虑多个指标。可以使用加权平均或
Pareto 最优解。
评估实验设计
正确的实验设计对评估推荐系统至关重要:
数据集划分 : - 训练集:用于训练模型 -
验证集:用于调参和模型选择 - 测试集:用于最终评估,不能用于调参
时间划分 :对于有时序性的数据,应该按时间划分,用历史数据训练,预测未来数据。
用户划分 :对于用户级别的评估,应该保证测试集中的用户不在训练集中(冷启动场景)。
评估协议 : - 留一法(
Leave-One-Out) :每个用户随机留一个物品作为测试 - K
折交叉验证 :将数据分成 K 份,每次用 K-1 份训练, 1 份测试 -
时间序列划分 :按时间顺序划分,模拟真实场景
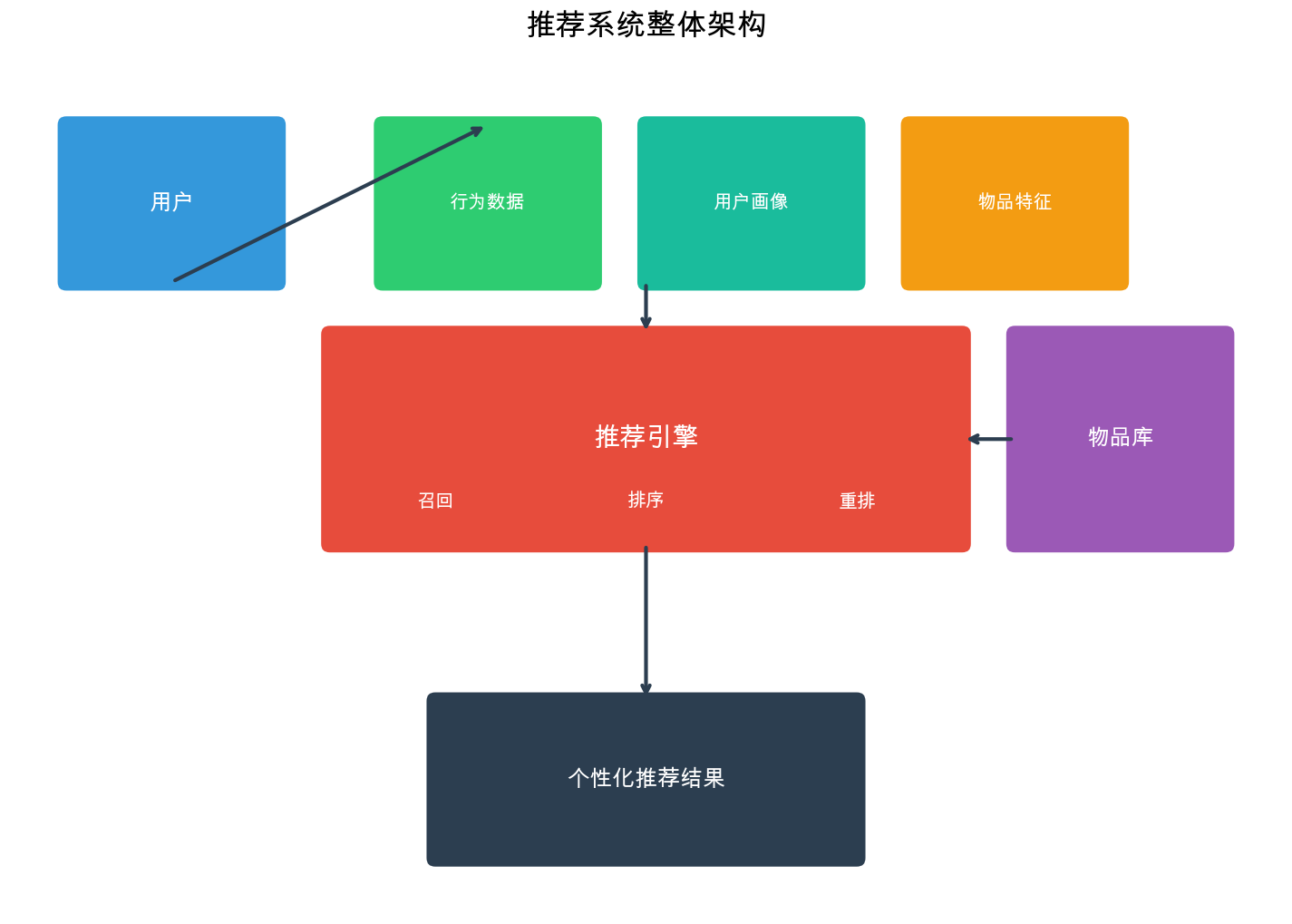
推荐系统架构
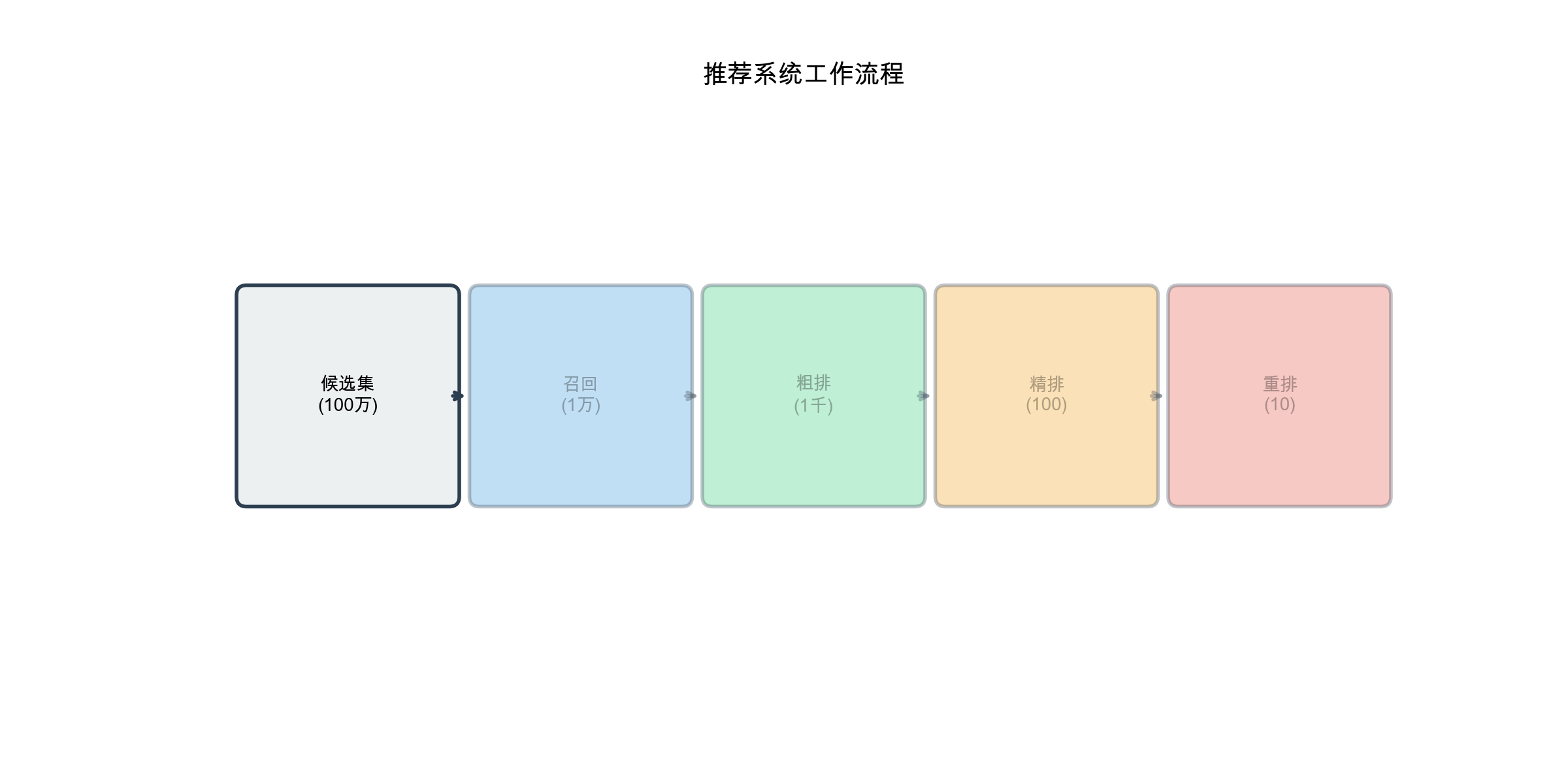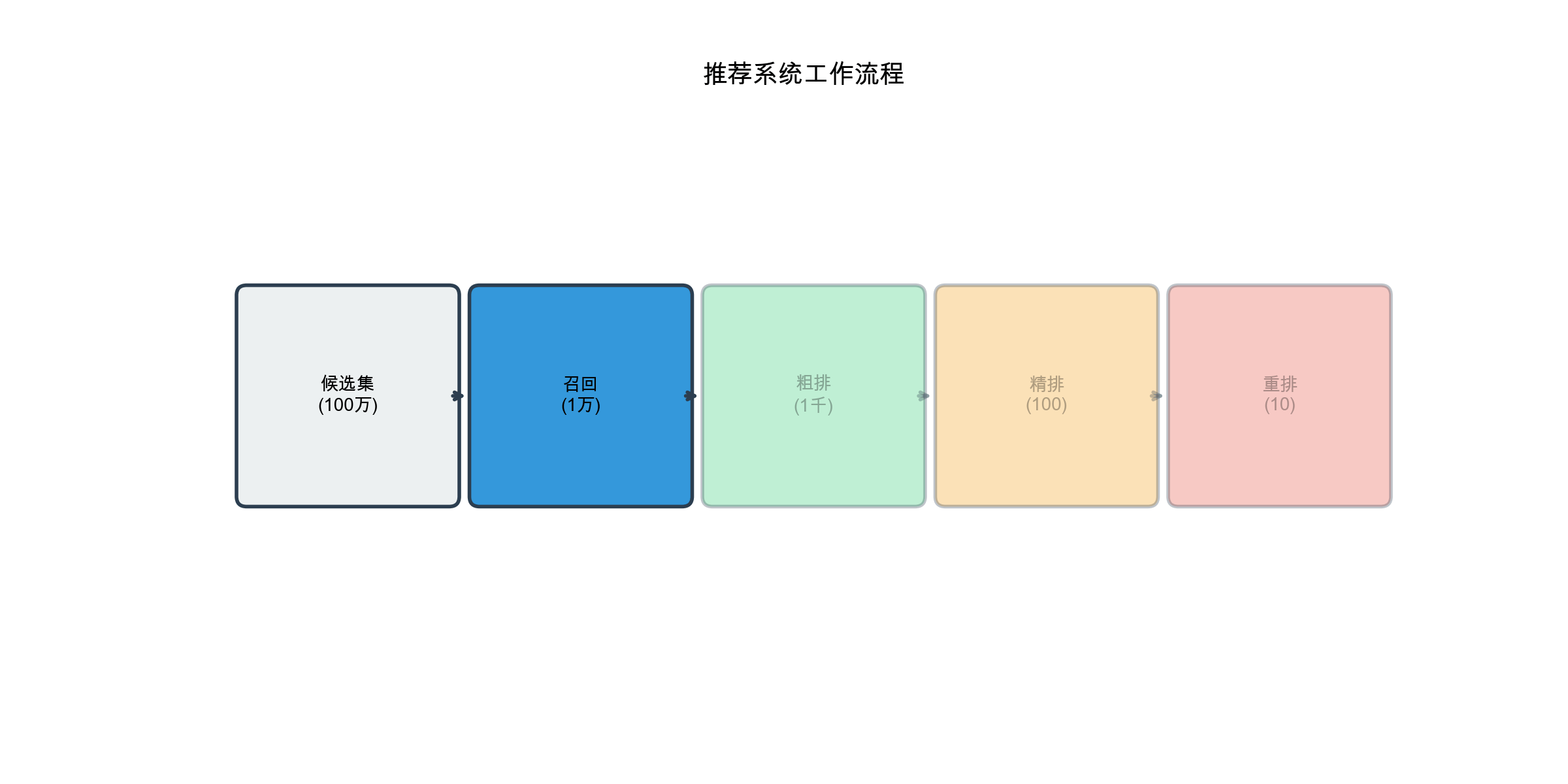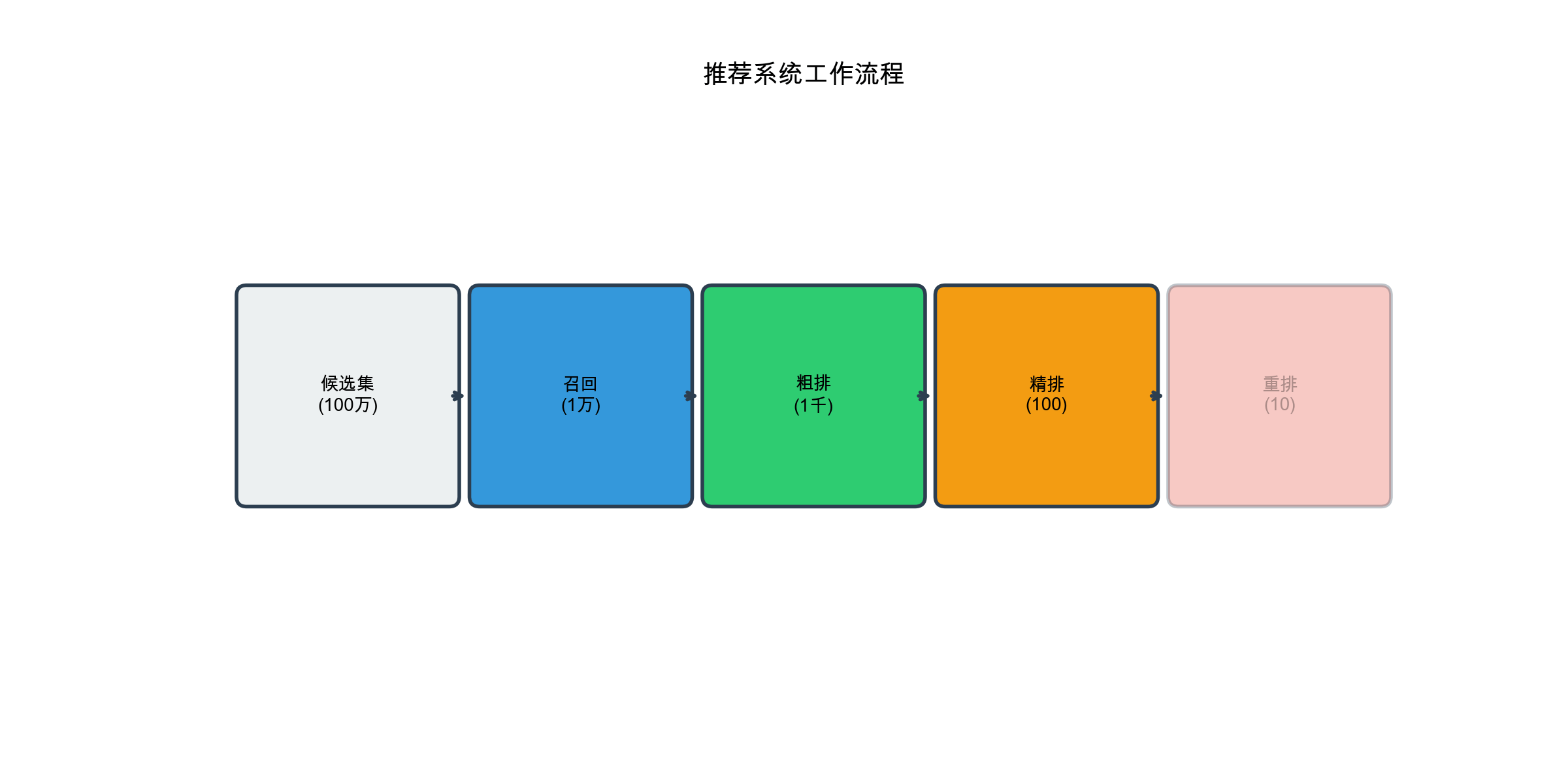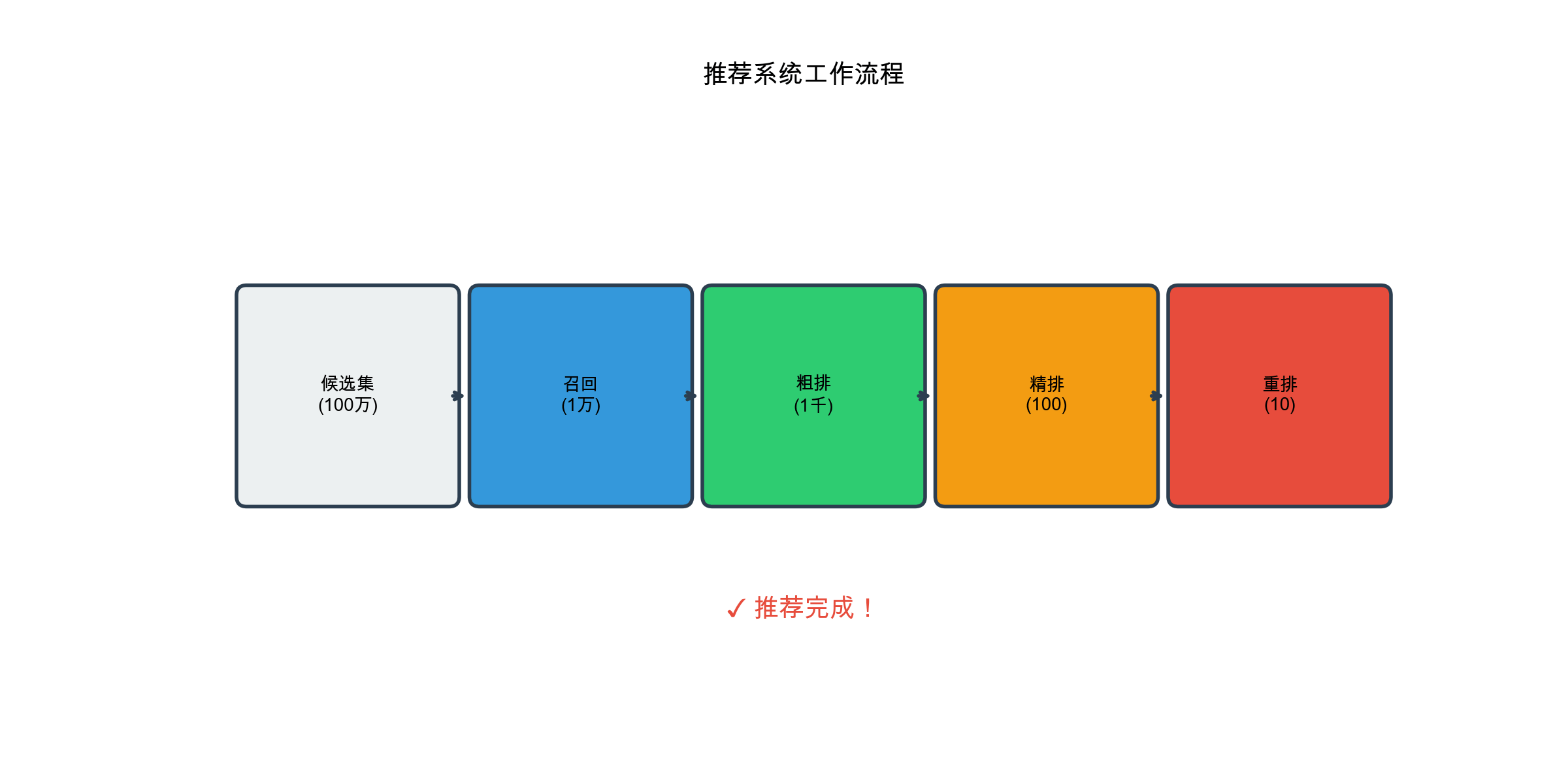
工业级推荐系统通常采用多阶段架构,分为召回 (
Recall)、粗排 ( Coarse
Ranking)、精排 ( Fine
Ranking)和重排 (
Reranking)四个阶段。这种架构在效果和效率之间取得了平衡。
1 2 3 4 5 6 7 8 9 10 11 用户请求 ↓ [召回层] ← 从百万级候选集中召回数千个物品 ↓ [粗排层] ← 用简单模型快速排序,保留数百个 ↓ [精排层] ← 用复杂模型精确排序,保留数十个 ↓ [重排层] ← 考虑多样性、新颖性等业务规则 ↓ 最终推荐列表
召回层( Recall)
召回层的目标是从百万甚至千万级的物品库中,快速召回数千个候选物品。召回层的特点:
速度快 :需要在几十毫秒内完成覆盖全 :不能漏掉用户可能感兴趣的物品模型简单 :通常使用简单的协同过滤、内容匹配或向量检索
常见的召回方法:
协同过滤召回 : - User-CF:找相似用户喜欢的物品 -
Item-CF:找用户历史喜欢物品的相似物品 -
矩阵分解:将用户和物品映射到低维空间,用向量相似度召回
内容召回 : - 关键词匹配 - 标签匹配 -
向量检索(如使用 Faiss 、 Milvus 等向量数据库)
热门召回 : - 全局热门 - 分类热门 - 实时热门
多路召回 :同时使用多种召回策略,合并结果。
粗排层( Coarse Ranking)
粗排层对召回的结果进行初步排序,目标是快速筛选出数百个更相关的物品。粗排层的特点:
速度较快 :需要在百毫秒级完成模型中等复杂度 :可以使用简单的机器学习模型(如 LR
、 GBDT)特征较少 :主要使用统计特征、用户画像特征
精排层( Fine Ranking)
精排层是推荐系统的核心,使用最复杂的模型和最丰富的特征,对粗排结果进行精确排序。精排层的特点:
模型复杂 :可以使用深度学习模型(如 Wide&Deep 、
DeepFM 、 DIN 等)特征丰富 :用户特征、物品特征、上下文特征、交叉特征等计算量大 :可以使用 GPU 加速
重排层( Reranking)
重排层在精排结果的基础上,考虑业务规则和多样性等约束,生成最终的推荐列表。重排层的特点:
规则驱动 :去重、打散、多样性保证、新颖性保证业务导向 :考虑商业目标(如 GMV 、 CTR 等)
常见的重排策略:
多样性打散 :避免连续推荐相同类别的物品
去重 :去除用户已经看过的物品
新颖性提升 :提升长尾物品的曝光
商业规则 :保证某些物品的曝光率
系统架构的工程实现
工业级推荐系统的架构设计需要考虑多个方面:
数据流设计
1 2 3 4 5 用户行为数据 → 实时流处理 → 特征存储 ↓ 离线批处理 → 模型训练 → 模型服务 ↓ 用户请求 → 召回服务 → 粗排服务 → 精排服务 → 重排服务 → 返回结果
特征工程
特征工程是推荐系统的关键环节:
用户特征 : - 静态特征:年龄、性别、地域、注册时间 -
动态特征:最近 N 天点击率、购买率、活跃度 -
行为序列:最近点击的物品序列、搜索关键词序列
物品特征 : - 静态特征:类别、价格、品牌、发布时间 -
动态特征:最近 N 天点击率、购买率、评分 -
内容特征:文本、图片、视频特征
上下文特征 : - 时间特征:小时、星期、是否节假日 -
位置特征: GPS 位置、 IP 地址 - 设备特征:设备类型、操作系统、浏览器
交叉特征 : -
用户-物品交叉:用户历史是否点击过该物品类别 -
用户-上下文交叉:用户在此时段的活跃度 -
物品-上下文交叉:物品在此时段的受欢迎程度
模型服务
模型服务需要考虑:
延迟要求 :精排层通常要求在 100ms 内返回结果并发能力 :需要支持高并发请求模型更新 :支持模型热更新,无需重启服务A/B 测试 :支持多版本模型同时在线
常用技术: - TensorFlow Serving : Google
的模型服务框架 - TorchServe : PyTorch 的模型服务框架 -
Redis :缓存特征和热门结果 -
Kafka :消息队列,用于实时特征更新
监控和告警
推荐系统需要完善的监控体系:
指标监控 : - 系统指标: QPS 、延迟、错误率 -
业务指标: CTR 、 GMV 、用户留存 - 模型指标:预测分数分布、特征分布
异常检测 : - 指标异常: CTR 突然下降、延迟突然上升 -
数据异常:特征分布偏移、数据缺失
告警机制 : - 实时告警:关键指标异常立即告警 -
定期报告:每日/每周效果报告
推荐系统的核心挑战
推荐系统在实际应用中面临诸多挑战,理解这些挑战有助于设计更好的系统。
冷启动问题
冷启动是指新用户或新物品缺乏历史数据,难以进行推荐。
新用户冷启动 : -
问题:新用户没有历史行为,无法计算用户相似度或构建用户画像 - 解决方案:
- 收集用户注册信息(年龄、性别、地域等),使用人口统计学特征 -
推荐热门物品 - 让用户选择兴趣标签 -
使用内容推荐(基于用户填写的兴趣)
新物品冷启动 : -
问题:新物品没有被用户评分或点击,难以被推荐 - 解决方案: -
使用内容特征(文本、图片、标签等) -
给予新物品一定的曝光机会(探索机制) - 使用多臂老虎机( Multi-Armed
Bandit)算法平衡探索和利用
数据稀疏性问题
推荐系统中,用户-物品评分矩阵通常非常稀疏。例如, Netflix
的评分矩阵稀疏度超过 99%,即 99% 以上的用户-物品对没有评分。
稀疏性的影响 : - 难以找到相似用户或相似物品 -
预测准确率下降 - 覆盖率低
解决方案 : -
矩阵分解 :将高维稀疏矩阵分解为低维稠密矩阵,学习用户和物品的潜在特征
-
隐式反馈 :利用点击、浏览时长等隐式反馈,数据量远大于显式评分
- 深度学习 :使用神经网络学习用户和物品的表示
长尾问题
长尾问题是指推荐系统倾向于推荐热门物品,而忽略小众但可能更符合用户兴趣的物品。
长尾问题的影响 : - 推荐结果同质化 -
小众创作者/商家难以获得曝光 - 用户体验下降(信息茧房)
解决方案 : -
多样性优化 :在排序时加入多样性约束 -
长尾提升 :给予长尾物品更高的权重 -
探索机制 :主动推荐一些长尾物品,收集反馈
可解释性问题
用户希望知道为什么推荐某个物品,但很多推荐算法(特别是深度学习模型)是黑盒,难以解释。
可解释性的价值 : - 增加用户信任 -
帮助用户理解推荐逻辑 - 便于调试和优化
解决方案 : - 使用可解释的模型(如
Item-CF:"因为你喜欢 A,所以推荐相似的 B") -
提供推荐理由(如"相似用户也喜欢"、"基于你的浏览历史") -
使用注意力机制可视化模型关注的特征
实时性问题
用户行为是动态的,推荐系统需要快速响应用户的最新兴趣变化。
实时性的挑战 : -
特征更新:用户特征、物品特征需要实时更新 -
模型更新:模型需要在线学习或定期更新 -
系统延迟:需要在毫秒级返回结果
解决方案 : - 流式计算 :使用 Flink
、 Spark Streaming 等实时计算框架 -
在线学习 :模型在线更新,无需重新训练 -
缓存优化 :缓存热门结果,减少计算
公平性问题
推荐系统可能存在偏见,对某些用户群体或物品类别不公平。
公平性的挑战 : -
算法偏见:模型可能学习到数据中的偏见 - 数据偏见:训练数据本身存在偏见 -
反馈循环:推荐结果影响用户行为,进一步强化偏见
解决方案 : - 公平性约束:在优化目标中加入公平性项 -
数据平衡:确保训练数据的多样性 - 定期审计:监控推荐结果的公平性
推荐系统的性能优化
推荐系统需要处理海量数据和实时请求,性能优化至关重要。
计算优化
相似度计算优化 : - 只计算有共同评分的用户对/物品对 -
使用稀疏矩阵存储和计算 - 并行计算:使用多线程或多进程
向量检索优化 : - 使用 Faiss 、 Milvus 等向量数据库 -
使用 LSH 、 HNSW 等近似最近邻算法 - 使用 GPU 加速
模型推理优化 : - 模型量化:将浮点数转换为低精度(如
int8) - 模型剪枝:移除不重要的神经元 - 模型蒸馏:用大模型训练小模型 -
批量推理:一次处理多个请求
存储优化
缓存策略 : - 热门结果缓存:缓存热门用户的推荐结果 -
特征缓存:缓存用户特征和物品特征 -
相似度缓存:缓存用户相似度和物品相似度
数据存储 : - 使用列式存储(如 Parquet)存储特征 -
使用 Redis 存储热点数据 - 使用 HBase/Cassandra 存储大规模数据
系统优化
负载均衡 : - 使用 Nginx 、 HAProxy 等负载均衡器 -
根据服务器负载动态分配请求
异步处理 : -
非关键路径异步处理(如日志记录、特征更新) - 使用消息队列解耦服务
降级策略 : - 当精排服务不可用时,使用粗排结果 -
当召回服务不可用时,返回热门结果
推荐系统的部署实践
开发环境
推荐系统的开发需要: -
数据环境 :训练数据、测试数据、线上数据 -
计算资源 : GPU 服务器用于模型训练 -
开发工具 : Jupyter Notebook 、 PyCharm 、 VS Code
测试环境
测试环境应该尽可能接近生产环境: -
数据 :使用生产数据的采样 -
配置 :使用与生产环境相同的配置 -
性能测试 :压力测试、延迟测试
生产环境
生产环境需要考虑: -
高可用 :多副本部署,避免单点故障 -
可扩展 :支持水平扩展 -
监控告警 :完善的监控和告警机制 -
灰度发布 :先在小流量上测试,再全量发布
版本管理
推荐系统的版本管理: -
模型版本 :记录模型版本、训练数据、超参数 -
特征版本 :记录特征定义和计算逻辑 -
代码版本 :使用 Git 管理代码 -
实验管理 :记录每次实验的配置和结果
基础算法实现
下面我们实现 User-CF 和 Item-CF 算法,使用 Python 和 NumPy 。
数据准备
在实现协同过滤算法之前,需要先准备测试数据。推荐系统的核心数据结构是用户-物品评分矩阵 。在实际应用中,这个矩阵通常非常大(百万用户
× 百万物品)且非常稀疏(用户只会对少数物品评分, 99%
以上的元素为空)。
为什么需要特殊的数据结构 ?
推荐系统的评分矩阵有两个特点: 1. 高维稀疏性 :
Netflix
有数亿用户和数万电影,但每个用户平均只评分几百部电影,矩阵稀疏度超过 99%
2.
动态更新 :用户会不断产生新的评分,需要支持高效的增删改查操作
如果使用传统的二维数组(如 NumPy 的
ndarray)存储,会浪费大量内存空间(存储大量 0
值),且查询效率低。因此,需要使用更适合稀疏数据的数据结构。
解决方案:嵌套字典结构
我们采用 Python 的嵌套字典来存储评分矩阵: -
外层字典 :键为用户 ID,值为该用户的所有评分记录 -
内层字典 :键为物品 ID,值为评分值
这种设计的优势: 1.
内存高效 :只存储非零元素,不存储空值 2.
查询快速 :O(1)
时间复杂度判断用户是否对某物品评分 3.
易于扩展 :添加新评分只需
ratings[user_id][item_id] = rating 4.
灵活性强 :可以轻松处理不同用户评分不同数量物品的情况
数据格式选择 :
我们使用 MovieLens 数据集格式的简化版本进行演示。 MovieLens
是推荐系统领域最常用的公开数据集,由 GroupLens
研究组维护,包含用户对电影的显式评分( 1-5
分)数据。在实际应用中,你可能需要: - 从 CSV 文件读取数据 -
处理时间戳信息(用于时间衰减) - 处理隐式反馈(点击、浏览时长等) -
数据清洗和预处理(去除异常值、处理缺失值)
下面我们展示如何构建和操作这种数据结构:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import numpy as np from collections import defaultdict from typing import List , Tuple , Dict ratings = { 1 : {1 : 5 , 2 : 4 , 3 : 3 , 4 : 5 }, 2 : {1 : 4 , 2 : 5 , 3 : 4 , 5 : 3 }, 3 : {2 : 3 , 3 : 5 , 4 : 4 , 5 : 5 }, 4 : {1 : 3 , 3 : 4 , 4 : 3 , 5 : 4 }, 5 : {2 : 5 , 4 : 5 , 5 : 4 } }
数据说明 :
这个示例数据集包含 5 个用户和 5 个物品,共 20
个评分记录。从数据中可以观察到:
数据稀疏性 :总共有 5 × 5=25
个可能的用户-物品对,但只有 20 个评分,稀疏度为
20%(实际推荐系统中稀疏度通常 < 1%)评分分布 :用户的评分习惯不同,有些用户倾向于打高分(如用户
5),有些用户评分较为分散共同评分 :部分用户对同一物品进行了评分(如物品 1
被用户 1 、 2 、 4 评分),这些共同评分是计算相似度的基础
数据准备代码深度解读
关键实现细节 :
嵌套字典的优势 :相比二维数组,嵌套字典在稀疏场景下内存占用更小。假设有
100 万用户和 10 万物品,但每个用户平均只评分 100 个物品:
二维数组:需要
1000000 × 100000 × 8 bytes ≈ 800 GB(假设 float64)
嵌套字典:只需要
1000000 × 100 × (8 + 8) bytes ≈ 1.6 GB(用户 ID + 物品 ID +
评分值)
内存节省:约 500 倍
查询效率 :判断用户 u 是否对物品
i 评分:
字典:item_id in ratings[user_id] → O(1)
平均时间复杂度
数组:需要遍历用户的所有评分 → O(k) 其中 k
是用户评分的物品数
数据扩展性 :当需要添加时间戳、评分来源等信息时,可以轻松扩展:
1 2 3 4 5 6 7 ratings_extended = { 1 : { 1 : {'rating' : 5 , 'timestamp' : 1234567890 , 'source' : 'web' }, 2 : {'rating' : 4 , 'timestamp' : 1234567900 , 'source' : 'mobile' } } }
常见问题与解决方案 :
问题
原因
解决方案
内存占用仍然很大
用户数量或物品数量非常大
使用稀疏矩阵库(如 scipy.sparse)或数据库存储
查询速度慢
字典嵌套层级深,或数据量过大
使用倒排索引(物品→用户映射)或向量数据库
数据不一致
多个数据源,格式不统一
建立统一的数据模型和验证规则
缺失值处理
用户未评分的物品如何处理
不存储缺失值(稀疏表示),预测时返回默认值
性能优化建议 :
大规模数据 :当用户数超过百万时,考虑:
使用 scipy.sparse.csr_matrix 或
scipy.sparse.csc_matrix 存储
使用数据库(如 Redis 、 HBase)存储评分数据
使用分布式存储(如 HDFS)
实时更新 :如果需要支持实时评分更新:
使用 Redis 等内存数据库缓存热点数据
使用消息队列(如 Kafka)异步更新
定期批量同步到持久化存储
数据预处理 :在实际应用中,通常需要:
去重 :同一用户对同一物品的多次评分,保留最新的异常值检测 :去除明显异常的评分(如 0
分或超过评分范围的值)数据归一化 :将评分归一化到 [0, 1]
区间,便于不同评分体系的数据融合
实际使用示例 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 import pandas as pddf = pd.read_csv('ratings.csv' ) ratings = {} for _, row in df.iterrows(): user_id = int (row['userId' ]) item_id = int (row['movieId' ]) rating = float (row['rating' ]) if user_id not in ratings: ratings[user_id] = {} ratings[user_id][item_id] = rating print (f"用户数: {len (ratings)} " )print (f"物品数: {len (set (item for items in ratings.values() for item in items.keys()))} " )print (f"总评分数: {sum (len (items) for items in ratings.values())} " )n_users = len (ratings) n_items = len (set (item for items in ratings.values() for item in items.keys())) n_ratings = sum (len (items) for items in ratings.values()) sparsity = 1 - n_ratings / (n_users * n_items) print (f"稀疏度: {sparsity:.4 f} " )
User-CF 实现
下面我们实现基于用户的协同过滤算法( User-CF)。 User-CF
的基本思路:找到与目标用户相似的用户,然后推荐这些相似用户喜欢但目标用户还没接触过的物品。
问题背景 :
User-CF
要解决的核心问题是:如何为新用户推荐他们可能感兴趣的物品?
当用户刚注册或历史行为很少时,我们无法直接基于用户自己的历史来推荐。
User-CF
的解决思路是"物以类聚,人以群分 "——找到与目标用户兴趣相似的其他用户,利用这些相似用户的偏好来预测目标用户的兴趣。
解决思路 :
User-CF 算法可以分为四个核心步骤:
计算用户相似度 :这是算法的核心。需要衡量两个用户的兴趣相似程度。常用的相似度度量包括:
余弦相似度 :关注评分向量的"方向"而非"长度",适合处理评分尺度不同的情况皮尔逊相关系数 :考虑用户评分习惯的差异,通过减去平均评分消除偏差调整余弦相似度 :在 Item-CF 中更常用,但在 User-CF
中也可以使用 构建相似度矩阵 :计算所有用户对之间的相似度,构建一个
n × n 的相似度矩阵( n
是用户数)。这一步是预处理阶段,可以离线完成。
预测评分 :对于目标用户未评分的物品,找到对该物品有评分且与目标用户最相似的
K 个用户( K 通常取 10-50),用这些用户的评分加权平均来预测:
其中
生成推荐 :对所有未评分物品预测评分后,按预测评分降序排序,取
Top-N 推荐给用户。
设计考虑 :
为什么用加权平均而不是简单平均 ?
相似度高的用户,其评分应该对预测结果影响更大
相似度为负的用户(兴趣相反)也应该考虑,但权重较小
加权平均能更好地利用相似度信息
为什么要减去平均评分 ?
不同用户有不同的评分习惯:有些用户习惯打高分( 4-5
分),有些习惯打低分( 2-3 分)
减去平均评分后,我们关注的是"相对偏好"而非"绝对评分"
例如:用户 A 对电影 1 打 5 分,用户 B 对电影 1 打 3 分。如果 A
的平均评分是 4.5, B 的平均评分是
2.5,那么他们的相对偏好都是"比平均水平高 0.5
分",说明他们都喜欢这部电影
K 值的选择 :
K 太小 (如
K=1-3):信息不足,预测不稳定,容易受噪声影响K 太大 (如
K>100):引入不相似的用户,降低预测准确率推荐范围 :通常取
10-50,可以通过交叉验证选择最优值 相似度计算的优化 :
只计算有共同评分的用户对(没有共同评分则相似度为 0)
只存储相似度 > 0 的用户对,节省存储空间
对于大规模系统,可以只保留每个用户的 Top-K 相似用户
算法流程回顾 : 1.
计算所有用户之间的相似度,构建用户相似度矩阵 2.
对于目标用户未评分的物品,找到对该物品有评分且与目标用户相似的 K 个用户
3. 用这 K 个相似用户的评分加权平均,预测目标用户的评分 4.
按预测评分排序,推荐 Top-N 物品
下面我们给出完整的实现,包含详细的注释和边界情况处理:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 class UserCF : """基于用户的协同过滤推荐算法 该类实现了 User-CF 的完整流程,包括: - 用户相似度计算(支持余弦相似度和皮尔逊相关系数) - 评分预测 - Top-N 推荐 """ def __init__ (self, k: int = 3 , similarity: str = 'cosine' ): """初始化 User-CF 模型 Args: k: 选择最相似的 k 个用户进行评分预测 - k 过小可能导致推荐不准确(信息不足) - k 过大会引入噪声(不太相似的用户) - 通常取 3-10 之间 similarity: 相似度计算方法 - 'cosine': 余弦相似度,适合评分尺度一致的情况 - 'pearson': 皮尔逊相关系数,考虑用户评分习惯差异 """ self.k = k self.similarity = similarity self.user_similarity = {} self.ratings = {} self.user_avg_ratings = {} def fit (self, ratings: Dict [int , Dict [int , float ]] ): """训练模型:计算用户相似度矩阵 这一步是 User-CF 的核心准备工作。需要: 1. 计算每个用户的平均评分(用于皮尔逊相关系数) 2. 计算所有用户对之间的相似度 时间复杂度: O(n ²× m),其中 n 是用户数, m 是平均每个用户的评分数 空间复杂度: O(n ²),需要存储所有用户对的相似度 Args: ratings: 用户-物品评分字典 {user_id: {item_id: rating }} 例如:{1: {1: 5, 2: 4}, 2: {1: 4, 3: 5 }} """ self.ratings = ratings self._compute_user_averages() self._compute_user_similarity() def _compute_user_averages (self ): """计算每个用户的平均评分 用户平均评分的用途: 1. 皮尔逊相关系数需要减去平均值,消除用户评分习惯的影响 2. 评分预测时,用作基准值(当无法找到相似用户时,返回用户平均评分) 例如:用户 A 习惯打 4-5 分,用户 B 习惯打 2-3 分 即使他们的偏好相似,直接比较评分值会产生误导 """ for user_id, items in self.ratings.items(): ratings_list = list (items.values()) self.user_avg_ratings[user_id] = np.mean(ratings_list) def _compute_user_similarity (self ): """计算用户相似度矩阵 这是 User-CF 最核心的步骤。我们计算所有用户对之间的相似度。 实现细节: 1. 只计算上三角矩阵( i < j),因为相似度是对称的: sim(u1, u2) = sim(u2, u1) 2. 只存储相似度 > 0 的用户对,节省存储空间 3. 同时存储 (u1, u2) 和 (u2, u1) 两个方向,方便后续查找 优化空间: - 对于大规模数据,可以只保留 Top-K 相似用户 - 可以使用 LSH(局部敏感哈希)加速相似度计算 """ users = list (self.ratings.keys()) n_users = len (users) for i in range (n_users): for j in range (i+1 , n_users): u1, u2 = users[i], users[j] sim = self._calculate_similarity(u1, u2) if sim > 0 : self.user_similarity[(u1, u2)] = sim self.user_similarity[(u2, u1)] = sim def _calculate_similarity (self, u1: int , u2: int ) -> float : """计算两个用户的相似度 相似度计算的前提是两个用户有共同评分的物品。 如果没有共同评分,相似度为 0(无法判断两个用户是否相似)。 Args: u1: 用户 1 的 ID u2: 用户 2 的 ID Returns: 相似度值,范围通常在[-1, 1]之间(对于皮尔逊相关系数)或[0, 1]之间(对于余弦相似度) """ items_u1 = set (self.ratings[u1].keys()) items_u2 = set (self.ratings[u2].keys()) common_items = items_u1 & items_u2 if len (common_items) == 0 : return 0.0 if self.similarity == 'cosine' : return self._cosine_similarity(u1, u2, common_items) elif self.similarity == 'pearson' : return self._pearson_similarity(u1, u2, common_items) else : raise ValueError(f"Unknown similarity: {self.similarity} " ) def _cosine_similarity (self, u1: int , u2: int , common_items: set ) -> float : """计算余弦相似度 余弦相似度衡量两个向量在高维空间中的夹角。 公式: cos(θ) = (u · v) / (||u|| × ||v||) 几何意义: - 如果两个用户的评分模式完全相同(方向一致),夹角为 0 °,余弦值为 1 - 如果评分模式完全相反,夹角为 180 °,余弦值为-1 - 如果评分模式正交(无关),夹角为 90 °,余弦值为 0 优势: - 只考虑向量方向,不考虑大小,因此对评分尺度不敏感 - 计算简单,效率高 Args: u1, u2: 两个用户的 ID common_items: 两个用户共同评分的物品集合 Returns: 余弦相似度,范围[-1, 1],值越大表示越相似 """ numerator = sum (self.ratings[u1][item] * self.ratings[u2][item] for item in common_items) sum_sq_u1 = sum (self.ratings[u1][item] ** 2 for item in common_items) sum_sq_u2 = sum (self.ratings[u2][item] ** 2 for item in common_items) denominator = np.sqrt(sum_sq_u1) * np.sqrt(sum_sq_u2) if denominator == 0 : return 0.0 return numerator / denominator def _pearson_similarity (self, u1: int , u2: int , common_items: set ) -> float : """计算皮尔逊相关系数 皮尔逊相关系数衡量两个变量的线性相关性。与余弦相似度不同,它先减去各自的均值。 公式:ρ = Σ[(r_ui - r ̄_u)(r_vi - r ̄_v)] / (σ_u × σ_v) 优势: - 考虑了用户的评分习惯差异 - 对评分的绝对值不敏感,只关注评分的趋势 - 例如:用户 A 所有评分都加 2 分,不影响与用户 B 的皮尔逊相关系数 适用场景: - 当用户评分习惯差异大时(有人喜欢打高分,有人喜欢打低分) - 需要消除评分基准线影响时 Args: u1, u2: 两个用户的 ID common_items: 两个用户共同评分的物品集合 Returns: 皮尔逊相关系数,范围[-1, 1] - 1 表示完全正相关(评分趋势完全一致) - -1 表示完全负相关(评分趋势完全相反) - 0 表示无相关性 """ avg_u1 = self.user_avg_ratings[u1] avg_u2 = self.user_avg_ratings[u2] numerator = sum ((self.ratings[u1][item] - avg_u1) * (self.ratings[u2][item] - avg_u2) for item in common_items) sum_sq_diff_u1 = sum ((self.ratings[u1][item] - avg_u1) ** 2 for item in common_items) sum_sq_diff_u2 = sum ((self.ratings[u2][item] - avg_u2) ** 2 for item in common_items) denominator = np.sqrt(sum_sq_diff_u1) * np.sqrt(sum_sq_diff_u2) if denominator == 0 : return 0.0 return numerator / denominator def predict (self, user_id: int , item_id: int ) -> float : """预测用户对物品的评分 预测流程: 1. 检查用户和物品是否存在,处理边界情况 2. 如果用户已经对该物品评分,直接返回原评分 3. 找到对该物品有评分且与目标用户相似的 K 个用户 4. 用这 K 个相似用户的评分加权平均,预测目标用户的评分 预测公式: r ̂_ui = r ̄_u + Σ[sim(u,v) × (r_vi - r ̄_v)] / Σ|sim(u,v)| 公式解释: - r ̄_u: 目标用户的平均评分(基准线) - sim(u,v): 用户 u 和 v 的相似度(权重) - (r_vi - r ̄_v): 用户 v 对物品 i 的评分减去其平均评分(消除用户评分习惯差异) - 最终预测值 = 基准线 + 相似用户的偏差加权平均 Args: user_id: 目标用户 ID item_id: 目标物品 ID Returns: 预测评分,范围[1.0, 5.0] """ if user_id not in self.ratings: return self.user_avg_ratings.get(user_id, 3.0 ) if item_id in self.ratings[user_id]: return self.ratings[user_id][item_id] similar_users = [] for other_user in self.ratings.keys(): if other_user == user_id: continue if item_id not in self.ratings[other_user]: continue sim_key = (user_id, other_user) if sim_key in self.user_similarity: similar_users.append((other_user, self.user_similarity[sim_key])) similar_users.sort(key=lambda x: x[1 ], reverse=True ) similar_users = similar_users[:self.k] if len (similar_users) == 0 : return self.user_avg_ratings.get(user_id, 3.0 ) numerator = 0.0 denominator = 0.0 avg_rating_u = self.user_avg_ratings[user_id] for other_user, sim in similar_users: rating = self.ratings[other_user][item_id] avg_rating_v = self.user_avg_ratings[other_user] numerator += sim * (rating - avg_rating_v) denominator += abs (sim) if denominator == 0 : return avg_rating_u predicted = avg_rating_u + numerator / denominator return max (1.0 , min (5.0 , predicted)) def recommend (self, user_id: int , n: int = 10 ) -> List [Tuple [int , float ]]: """为用户推荐 Top-N 物品 推荐流程: 1. 找到用户未评分的所有候选物品 2. 对每个候选物品预测评分 3. 按预测评分降序排序 4. 返回 Top-N 物品 Args: user_id: 目标用户 ID n: 推荐物品数量 Returns: 推荐列表:[(item_id, predicted_rating), ...] 按 predicted_rating 降序排列 """ if user_id not in self.ratings: return [] user_items = set (self.ratings[user_id].keys()) all_items = set () for items in self.ratings.values(): all_items.update(items.keys()) candidate_items = all_items - user_items predictions = [] for item_id in candidate_items: pred_rating = self.predict(user_id, item_id) predictions.append((item_id, pred_rating)) predictions.sort(key=lambda x: x[1 ], reverse=True ) return predictions[:n]
User-CF 代码深度解读
关键实现细节 :
相似度计算的对称性优化 (第 815-823 行):
我们只计算上三角矩阵(i < j),因为相似度是对称的:sim(u1, u2) = sim(u2, u1)
同时存储 (u1, u2) 和 (u2, u1)
两个方向,方便后续查找
这种设计在用户数较少时内存开销可接受,但在大规模系统中应该只存储
Top-K 相似用户
余弦相似度的几何意义 (第 855-892 行):
余弦相似度衡量的是两个向量在高维空间中的夹角,而非距离
即使两个用户给的分数不同(向量长度不同),只要他们对不同物品的偏好模式一致(方向相同),相似度就会很高
例如:用户 A 对物品 1-3 的评分是 [5, 4, 3],用户 B 的评分是 [10, 8,
6],虽然 B 的分数更高,但他们的偏好模式相同,余弦相似度为 1.0
皮尔逊相关系数的优势 (第 894-941 行):
通过减去平均评分,消除了用户评分习惯的影响
例如:用户 A 习惯打高分(平均 4.5 分),用户 B 习惯打低分(平均 2.5
分),但他们对物品的相对偏好可能相同
皮尔逊相关系数能捕捉到这种"相对偏好"的相似性
预测公式的数学原理 (第 1171-1172 行):
公式:
第二部分是相似用户的"偏差"加权平均,权重是相似度
这种设计既考虑了用户的整体评分水平,又考虑了相似用户的偏好偏差
设计权衡 :
相似度存储 vs 计算时间 :
当前设计 :预先计算所有用户对的相似度,存储空间
替代方案 :按需计算相似度,存储空间 选择 :对于中小规模系统(用户数 < 10
万),预先计算更高效;对于大规模系统,应该只存储 Top-K 相似用户 K 值的选择 :
K 太小 :信息不足,预测不稳定,容易受噪声影响K
太大 :引入不相似的用户,降低预测准确率,计算开销增大实践建议 :通过交叉验证选择,通常取 10-50 相似度度量的选择 :
余弦相似度 :计算简单,但对评分尺度敏感皮尔逊相关系数 :考虑了用户评分习惯差异,但计算稍复杂选择建议 :如果用户评分习惯差异大,使用皮尔逊;否则使用余弦相似度
常见问题与解决方案 :
问题
原因
解决方案
推荐结果都是热门物品
只考虑相似度,没有考虑物品流行度
加入 IDF 惩罚:
冷启动用户无推荐
新用户没有评分历史,无法计算相似度
结合内容推荐或使用全局热门作为初始推荐
计算太慢
相似度矩阵太大,或用户数太多
使用 LSH(局部敏感哈希)或 FAISS 等 ANN 算法加速相似度计算
推荐不够多样
Top-K 邻居兴趣太集中
增大 K 值,或在推荐时加入多样性约束( MMR 算法)
内存占用过大
存储所有用户对的相似度
只存储每个用户的 Top-K 相似用户,或使用稀疏矩阵存储
性能优化建议 :
时间复杂度分析 :
相似度计算 :预测评分 :推荐生成 : 大规模系统优化 :
近似最近邻( ANN) :使用 LSH 、 FAISS
等工具加速相似度计算分布式计算 :使用 MapReduce 或 Spark
并行计算相似度矩阵增量更新 :当新用户加入时,只计算与新用户相关的相似度,而非重新计算整个矩阵 实际使用示例 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 from sklearn.model_selection import train_test_splitratings = { 1 : {1 : 5 , 2 : 4 , 3 : 3 , 4 : 5 }, 2 : {1 : 4 , 2 : 5 , 3 : 4 , 5 : 3 }, 3 : {2 : 3 , 3 : 5 , 4 : 4 , 5 : 5 }, 4 : {1 : 3 , 3 : 4 , 4 : 3 , 5 : 4 }, 5 : {2 : 5 , 4 : 5 , 5 : 4 } } user_cf = UserCF(k=3 , similarity='cosine' ) user_cf.fit(ratings) recommendations = user_cf.recommend(user_id=1 , n=5 ) print ("推荐结果:" )for item_id, score in recommendations: print (f" 物品 {item_id} : 预测评分 {score:.2 f} " ) predicted_rating = user_cf.predict(user_id=1 , item_id=5 ) print (f"\n 用户 1 对物品 5 的预测评分: {predicted_rating:.2 f} " )print ("\n 与用户 1 最相似的用户:" )similar_users = [] for other_user in ratings.keys(): if other_user != 1 : sim_key = (1 , other_user) if sim_key in user_cf.user_similarity: similar_users.append((other_user, user_cf.user_similarity[sim_key])) similar_users.sort(key=lambda x: x[1 ], reverse=True ) for user_id, sim in similar_users[:3 ]: print (f" 用户 {user_id} : 相似度 {sim:.3 f} " )
与 Item-CF 的对比 :
特性
User-CF
Item-CF
相似度基础
用户相似度
物品相似度
稳定性
用户兴趣变化快,相似度不稳定
物品特征变化慢,相似度更稳定
可解释性
"相似用户也喜欢"
"因为你喜欢 A,所以推荐相似的 B"(更好)
计算效率
用户数通常 > 物品数,计算量大
物品数通常 < 用户数,计算量小
适用场景
用户数少,物品数多
物品数少,用户数多(更常用)
在实际应用中,Item-CF
通常表现更好 ,因为物品相似度更稳定,且可解释性更强。但 User-CF
也有其优势:能发现用户的潜在兴趣(通过相似用户),对用户兴趣变化更敏感。
Item-CF 实现
下面实现基于物品的协同过滤算法( Item-CF)。 Item-CF 与 User-CF
的思路类似,但是基于物品相似度而非用户相似度。 Item-CF
的基本思路:找到与用户历史喜欢的物品相似的物品,推荐给用户。
问题背景 :
Item-CF
要解决的核心问题是:如何基于用户的历史偏好,推荐他们可能感兴趣的新物品?
与 User-CF 不同, Item-CF
关注的是物品之间的相似性,而非用户之间的相似性。这种方法的直觉是:如果用户喜欢物品
A,而物品 B 与物品 A 相似,那么用户很可能也会喜欢物品 B 。
为什么 Item-CF 通常比 User-CF 更好?
稳定性 :物品的特征(如电影的类型、导演、演员)变化很慢,而用户的兴趣可能快速变化。因此,物品相似度比用户相似度更稳定,不需要频繁重新计算。
计算效率 :在大多数推荐场景中,物品数量远少于用户数量(例如,
Netflix
有数亿用户,但只有数万部电影)。计算物品相似度矩阵的计算量和存储空间都更小。
可解释性 : Item-CF
的推荐理由更直观:"因为你喜欢《肖申克的救赎》,所以我们推荐相似的《阿甘正传》"。这种解释更容易被用户理解和接受。
实时性 :物品相似度可以提前离线计算好,在线推荐时只需要简单的查表和加权平均,延迟很低。
解决思路 :
Item-CF 算法可以分为四个核心步骤:
计算物品相似度 :这是算法的核心。需要衡量两个物品的相似程度。常用的相似度度量包括:
余弦相似度 :基于用户对两个物品的评分向量计算调整余弦相似度 (推荐使用):减去用户平均评分,消除用户评分习惯的影响。这是
Item-CF 的标准做法。 构建相似度矩阵 :计算所有物品对之间的相似度,构建一个
m × m 的相似度矩阵( m
是物品数)。这一步可以离线完成,定期更新。
预测评分 :对于用户未评分的物品
其中
生成推荐 :对所有未评分物品预测评分后,按预测评分降序排序,取
Top-N 推荐给用户。
设计考虑 :
为什么 Item-CF 不需要减去平均评分?
与 User-CF 不同, Item-CF
的预测公式直接使用评分值,而不是偏差值
这是因为我们关注的是"用户对相似物品的评分",而不是"用户评分习惯的偏差"
但在计算相似度时,我们仍然使用调整余弦相似度(减去用户平均评分),以消除用户评分习惯的影响
调整余弦相似度的重要性 :
假设用户 A 习惯打高分(平均 4.5 分),用户 B 习惯打低分(平均 2.5
分)
如果他们都对物品 1 打 5 分,对物品 2 打 4 分,那么:
普通余弦相似度:可能认为两个物品不相似(因为评分值差异大)
调整余弦相似度:减去平均分后,两个用户对两个物品的相对偏好都是"比平均水平高
0.5 分",能正确识别相似性
K 值的选择 :
与 User-CF 类似, K 值的选择需要在准确率和稳定性之间权衡
通常取 10-50,可以通过交叉验证选择最优值
算法流程 : 1.
计算所有物品之间的相似度,构建物品相似度矩阵 2. 对于用户未评分的物品
i,找到与 i 相似且用户已评分的 K 个物品 3. 用这 K
个相似物品的评分加权平均,预测用户对物品 i 的评分 4.
按预测评分排序,推荐 Top-N 物品
下面我们给出完整的实现,特别关注调整余弦相似度的计算:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 class ItemCF : """基于物品的协同过滤推荐算法 该类实现了 Item-CF 的完整流程,包括: - 物品相似度计算(支持余弦相似度和调整余弦相似度) - 评分预测 - Top-N 推荐 """ def __init__ (self, k: int = 3 , similarity: str = 'cosine' ): """初始化 Item-CF 模型 Args: k: 选择最相似的 k 个物品进行评分预测 通常取 3-10 之间 similarity: 相似度计算方法 - 'cosine': 余弦相似度 - 'adjusted_cosine': 调整余弦相似度(推荐使用) 调整余弦相似度减去用户平均评分,消除用户评分习惯的影响 """ self.k = k self.similarity = similarity self.item_similarity = {} self.ratings = {} self.item_avg_ratings = {} def fit (self, ratings: Dict [int , Dict [int , float ]] ): """训练模型:计算物品相似度矩阵 Args: ratings: 用户-物品评分字典 """ self.ratings = ratings self._compute_item_averages() self._compute_item_similarity() def _compute_item_averages (self ): """计算每个物品的平均评分 物品平均评分用途: 1. 作为默认返回值(当无法预测评分时) 2. 可以用来评估物品的整体受欢迎程度 """ item_ratings = defaultdict(list ) for user_id, items in self.ratings.items(): for item_id, rating in items.items(): item_ratings[item_id].append(rating) for item_id, ratings_list in item_ratings.items(): self.item_avg_ratings[item_id] = np.mean(ratings_list) def _compute_item_similarity (self ): """计算物品相似度矩阵 实现策略: 1. 先构建物品-用户倒排索引,方便查找评分过某个物品的所有用户 2. 遍历所有物品对,计算相似度 3. 只存储相似度 > 0 的物品对 """ item_users = defaultdict(set ) for user_id, items in self.ratings.items(): for item_id in items.keys(): item_users[item_id].add(user_id) items = list (item_users.keys()) n_items = len (items) for i in range (n_items): for j in range (i+1 , n_items): item1, item2 = items[i], items[j] sim = self._calculate_similarity(item1, item2) if sim > 0 : self.item_similarity[(item1, item2)] = sim self.item_similarity[(item2, item1)] = sim def _calculate_similarity (self, item1: int , item2: int ) -> float : """计算两个物品的相似度 Args: item1, item2: 两个物品的 ID Returns: 相似度值 """ users_item1 = set () users_item2 = set () for user_id, items in self.ratings.items(): if item1 in items: users_item1.add(user_id) if item2 in items: users_item2.add(user_id) common_users = users_item1 & users_item2 if len (common_users) == 0 : return 0.0 if self.similarity == 'cosine' : return self._cosine_similarity(item1, item2, common_users) elif self.similarity == 'adjusted_cosine' : return self._adjusted_cosine_similarity(item1, item2, common_users) else : raise ValueError(f"Unknown similarity: {self.similarity} " ) def _cosine_similarity (self, item1: int , item2: int , common_users: set ) -> float : """计算物品的余弦相似度 与用户相似度计算类似,但是基于用户维度而非物品维度 """ numerator = sum (self.ratings[user][item1] * self.ratings[user][item2] for user in common_users) sum_sq_item1 = sum (self.ratings[user][item1] ** 2 for user in common_users) sum_sq_item2 = sum (self.ratings[user][item2] ** 2 for user in common_users) denominator = np.sqrt(sum_sq_item1) * np.sqrt(sum_sq_item2) if denominator == 0 : return 0.0 return numerator / denominator def _adjusted_cosine_similarity (self, item1: int , item2: int , common_users: set ) -> float : """计算调整余弦相似度(减去用户平均评分) 调整余弦相似度是 Item-CF 的推荐做法,它消除了用户评分习惯的影响。 例如: - 用户 A 喜欢打高分( 4-5 分),对物品 1 打 5 分,对物品 2 打 4 分 - 用户 B 喜欢打低分( 2-3 分),对物品 1 打 3 分,对物品 2 打 2 分 如果使用普通余弦相似度,两个物品的相似度会受到用户评分习惯的影响。 但如果我们先减去用户的平均评分: - 用户 A:物品 1=5-4.5=0.5,物品 2=4-4.5=-0.5 - 用户 B:物品 1=3-2.5=0.5,物品 2=2-2.5=-0.5 可以看到,两个用户对两个物品的评分模式是一致的,都是"物品 1 比物品 2 好"。 调整余弦相似度能够捕捉到这种模式。 """ numerator = 0.0 sum_sq_diff_item1 = 0.0 sum_sq_diff_item2 = 0.0 for user in common_users: user_avg = np.mean(list (self.ratings[user].values())) diff1 = self.ratings[user][item1] - user_avg diff2 = self.ratings[user][item2] - user_avg numerator += diff1 * diff2 sum_sq_diff_item1 += diff1 ** 2 sum_sq_diff_item2 += diff2 ** 2 denominator = np.sqrt(sum_sq_diff_item1) * np.sqrt(sum_sq_diff_item2) if denominator == 0 : return 0.0 return numerator / denominator def predict (self, user_id: int , item_id: int ) -> float : """预测用户对物品的评分 Item-CF 的预测公式: r ̂_ui = Σ[sim(i,j) × r_uj] / Σ|sim(i,j)| 与 User-CF 不同, Item-CF 不需要减去平均评分,直接用评分加权平均。 Args: user_id: 目标用户 ID item_id: 目标物品 ID Returns: 预测评分,范围[1.0, 5.0] """ if user_id not in self.ratings: return self.item_avg_ratings.get(item_id, 3.0 ) if item_id in self.ratings[user_id]: return self.ratings[user_id][item_id] user_items = self.ratings[user_id] similar_items = [] for rated_item in user_items.keys(): sim_key = (item_id, rated_item) if sim_key in self.item_similarity: similar_items.append((rated_item, self.item_similarity[sim_key])) similar_items.sort(key=lambda x: x[1 ], reverse=True ) similar_items = similar_items[:self.k] if len (similar_items) == 0 : return self.item_avg_ratings.get(item_id, 3.0 ) numerator = 0.0 denominator = 0.0 for similar_item, sim in similar_items: rating = self.ratings[user_id][similar_item] numerator += sim * rating denominator += abs (sim) if denominator == 0 : return self.item_avg_ratings.get(item_id, 3.0 ) predicted = numerator / denominator return max (1.0 , min (5.0 , predicted)) def recommend (self, user_id: int , n: int = 10 ) -> List [Tuple [int , float ]]: """为用户推荐 Top-N 物品""" if user_id not in self.ratings: return [] user_items = set (self.ratings[user_id].keys()) all_items = set () for items in self.ratings.values(): all_items.update(items.keys()) candidate_items = all_items - user_items predictions = [] for item_id in candidate_items: pred_rating = self.predict(user_id, item_id) predictions.append((item_id, pred_rating)) predictions.sort(key=lambda x: x[1 ], reverse=True ) return predictions[:n]
Item-CF 代码深度解读
关键实现细节 :
倒排索引的构建 (第 1441-1446 行):
我们构建了物品到用户的倒排索引 item_users,格式为
{item_id: {user_id1, user_id2, ...}}
这种数据结构使得查找"评分过某个物品的所有用户"变得非常高效(
如果没有倒排索引,需要遍历所有用户,时间复杂度为
调整余弦相似度的计算 (第 1527-1561 行):
这是 Item-CF 的核心创新点。对于每个共同用户,我们计算:
diff1 = rating(item1) - user_avg:用户对物品 1
的评分减去该用户的平均评分diff2 = rating(item2) - user_avg:用户对物品 2
的评分减去该用户的平均评分
然后计算 diff1 * diff2 的累加和作为分子
这种设计消除了用户评分习惯的影响,只关注"相对偏好"
预测公式的简化 (第 1605-1613 行):
Item-CF 的预测公式比 User-CF 更简单:
直接用用户对相似物品的评分加权平均即可
用户平均评分的即时计算 (第 1549 行):
在计算调整余弦相似度时,我们对每个用户即时计算平均评分:user_avg = np.mean(list(self.ratings[user].values()))
优化建议 :可以预先计算并缓存用户平均评分,避免重复计算。对于大规模系统,这种优化能显著提升性能。
设计权衡 :
相似度计算的优化 :
当前实现 :遍历所有物品对,时间复杂度 优化方案
1 :只计算有共同用户的物品对,使用倒排索引加速优化方案 2 :对于大规模系统,使用 MapReduce 或 Spark
并行计算优化方案 3 :只存储每个物品的 Top-K
相似物品,节省存储空间 调整余弦相似度 vs 普通余弦相似度 :
调整余弦相似度 :消除了用户评分习惯的影响,更准确,但计算稍复杂普通余弦相似度 :计算简单,但对用户评分习惯敏感选择建议 :除非有特殊原因,否则应该使用调整余弦相似度 K 值的选择 :
与 User-CF 类似, K 值需要在准确率和稳定性之间权衡
通常取 10-50,可以通过交叉验证选择最优值
注意 :如果用户历史评分的物品数少于
K,则使用所有已评分物品
常见问题与解决方案 :
问题
原因
解决方案
新物品无法被推荐
新物品没有评分历史,无法计算相似度
使用内容特征计算相似度,或给予新物品一定的曝光机会(探索机制)
热门物品总是被推荐
热门物品与很多物品都有相似度,容易被推荐
加入流行度惩罚:
计算太慢
物品数量很大,相似度矩阵计算量大
使用 LSH 、 FAISS 等工具加速,或只计算 Top-K 相似物品
内存占用过大
存储所有物品对的相似度
只存储每个物品的 Top-K 相似物品,或使用稀疏矩阵存储
相似度计算不准确
共同用户太少,相似度不稳定
设置最小共同用户数阈值(如至少 5 个共同用户才计算相似度)
性能优化建议 :
时间复杂度分析 :
相似度计算 :预测评分 :推荐生成 : 大规模系统优化 :
并行计算 :使用 MapReduce 或 Spark
并行计算物品相似度矩阵增量更新 :当新物品加入时,只计算与新物品相关的相似度近似算法 :使用 LSH 、 FAISS
等工具加速相似度计算缓存优化 :缓存热门物品的相似物品列表,减少重复计算 实际使用示例 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 from sklearn.model_selection import train_test_splitratings = { 1 : {1 : 5 , 2 : 4 , 3 : 3 , 4 : 5 }, 2 : {1 : 4 , 2 : 5 , 3 : 4 , 5 : 3 }, 3 : {2 : 3 , 3 : 5 , 4 : 4 , 5 : 5 }, 4 : {1 : 3 , 3 : 4 , 4 : 3 , 5 : 4 }, 5 : {2 : 5 , 4 : 5 , 5 : 4 } } for similarity in ['cosine' , 'adjusted_cosine' ]: print (f"\n 使用 {similarity} 相似度:" ) item_cf = ItemCF(k=3 , similarity=similarity) item_cf.fit(ratings) recommendations = item_cf.recommend(user_id=1 , n=5 ) print ("推荐结果:" ) for item_id, score in recommendations: print (f" 物品 {item_id} : 预测评分 {score:.2 f} " ) print ("\n 物品相似度示例(物品 1 与其他物品):" ) for item_id in [2 , 3 , 4 , 5 ]: sim_key = (1 , item_id) if sim_key in item_cf.item_similarity: sim = item_cf.item_similarity[sim_key] print (f" 物品 1 与 物品{item_id} 的相似度: {sim:.3 f} " )
与 User-CF 的对比总结 :
维度
User-CF
Item-CF
相似度基础 用户相似度
物品相似度
稳定性 用户兴趣变化快,相似度不稳定
物品特征变化慢,相似度更稳定 ⭐
可解释性 "相似用户也喜欢"
"因为你喜欢 A,所以推荐相似的 B" ⭐
计算效率 用户数通常 > 物品数,计算量大
物品数通常 < 用户数,计算量小 ⭐
存储需求
实时性 需要实时计算用户相似度
可以提前离线计算物品相似度 ⭐
适用场景 用户数少,物品数多,用户兴趣变化快
物品数少,用户数多(更常见) ⭐
结论 :在实际应用中,Item-CF
通常表现更好 ,因为物品相似度更稳定,计算效率更高,且可解释性更强。这也是为什么
Amazon 、 Netflix 等大型推荐系统主要使用 Item-CF 的原因。但 User-CF
也有其价值:能发现用户的潜在兴趣,对用户兴趣变化更敏感,适合用户兴趣快速变化的场景。
使用示例
下面展示如何使用我们实现的 User-CF 和 Item-CF
算法。我们将使用前面定义的示例数据,演示完整的训练和推荐流程。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 ratings = { 1 : {1 : 5 , 2 : 4 , 3 : 3 , 4 : 5 }, 2 : {1 : 4 , 2 : 5 , 3 : 4 , 5 : 3 }, 3 : {2 : 3 , 3 : 5 , 4 : 4 , 5 : 5 }, 4 : {1 : 3 , 3 : 4 , 4 : 3 , 5 : 4 }, 5 : {2 : 5 , 4 : 5 , 5 : 4 } } print ("=" * 50 )print ("User-CF 推荐示例" )print ("=" * 50 )user_cf = UserCF(k=3 , similarity='cosine' ) user_cf.fit(ratings) recommendations = user_cf.recommend(user_id=1 , n=5 ) print ("\nUser-CF 推荐结果:" )for item_id, score in recommendations: print (f" 物品 {item_id} : 预测评分 {score:.2 f} " ) pred = user_cf.predict(user_id=1 , item_id=5 ) print (f"\n 用户 1 对物品 5 的预测评分: {pred:.2 f} " )print ("\n" + "=" * 50 )print ("Item-CF 推荐示例" )print ("=" * 50 )item_cf = ItemCF(k=3 , similarity='cosine' ) item_cf.fit(ratings) recommendations = item_cf.recommend(user_id=1 , n=5 ) print ("\nItem-CF 推荐结果:" )for item_id, score in recommendations: print (f" 物品 {item_id} : 预测评分 {score:.2 f} " )
运行结果分析 :
User-CF 和 Item-CF 的推荐结果可能略有不同,这是因为: 1.
相似度基础不同 : User-CF 基于用户相似度, Item-CF
基于物品相似度 2. 信息来源不同 : User-CF
利用相似用户的偏好, Item-CF 利用用户自己对相似物品的偏好 3.
稳定性不同 : Item-CF 通常更稳定,因为物品特征变化慢
在实际应用中,两种方法各有优势,可以结合使用(混合推荐)。
评估指标实现
推荐系统的评估指标是衡量推荐效果的重要工具。下面我们实现几个常用的评估指标,包括
Precision@K 、 Recall@K 、 AP@K 、 DCG@K 和 NDCG@K 。
评估指标的作用 : -
Precision@K :推荐列表中有多少是用户真正喜欢的(准确率)
- Recall@K :用户喜欢的物品中有多少被推荐了(召回率) -
AP@K :考虑位置信息的平均准确率 -
NDCG@K :考虑位置折扣和相关性等级的归一化折扣累积增益
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 def precision_at_k (recommended: List [int ], relevant: List [int ], k: int ) -> float : """计算 Precision@K Precision@K 衡量推荐列表前 K 个物品中,有多少是用户真正感兴趣的。 公式: Precision@K = |推荐列表 ∩ 相关物品| / K 取值范围:[0, 1] - 1 表示推荐的 K 个物品都是相关的(完美推荐) - 0 表示推荐的 K 个物品都不相关(完全失败) Args: recommended: 推荐列表(按推荐顺序排列) relevant: 用户真正感兴趣的物品列表(测试集) k: 只考虑前 K 个推荐 Returns: Precision@K 值 示例: recommended = [1, 2, 3, 4, 5] relevant = [2, 4, 6] precision_at_k(recommended, relevant, 5) = 2/5 = 0.4 (推荐的 5 个物品中,物品 2 和 4 是相关的) """ recommended_k = set (recommended[:k]) relevant_set = set (relevant) if len (recommended_k) == 0 : return 0.0 return len (recommended_k & relevant_set) / len (recommended_k) def recall_at_k (recommended: List [int ], relevant: List [int ], k: int ) -> float : """计算 Recall@K Recall@K 衡量用户真正感兴趣的物品中,有多少被推荐系统找到了。 公式: Recall@K = |推荐列表 ∩ 相关物品| / |相关物品| 取值范围:[0, 1] - 1 表示所有相关物品都被推荐了(完全召回) - 0 表示没有相关物品被推荐(完全遗漏) Args: recommended: 推荐列表 relevant: 相关物品列表 k: 只考虑前 K 个推荐 Returns: Recall@K 值 示例: recommended = [1, 2, 3, 4, 5] relevant = [2, 4, 6] recall_at_k(recommended, relevant, 5) = 2/3 = 0.667 (相关的 3 个物品中,物品 2 和 4 被推荐了) """ recommended_k = set (recommended[:k]) relevant_set = set (relevant) if len (relevant_set) == 0 : return 0.0 return len (recommended_k & relevant_set) / len (relevant_set) def ap_at_k (recommended: List [int ], relevant: List [int ], k: int ) -> float : """计算 Average Precision@K AP@K 考虑了推荐列表中的位置信息。相关物品出现在越靠前的位置, AP 值越高。 公式: AP@K = (1/|相关物品|) × Σ [Precision@i × rel(i)] 其中 rel(i) = 1 如果位置 i 的物品相关,否则为 0 直观理解: - 如果相关物品都排在前面, AP 值高 - 如果相关物品都排在后面, AP 值低 - AP 兼顾了准确率和排序质量 Args: recommended: 推荐列表(按推荐顺序) relevant: 相关物品列表 k: 只考虑前 K 个推荐 Returns: AP@K 值 示例: recommended = [1, 2, 3, 4, 5] relevant = [2, 4] 位置 1(物品 1):不相关,跳过 位置 2(物品 2):相关, Precision@2 = 1/2 = 0.5 位置 3(物品 3):不相关,跳过 位置 4(物品 4):相关, Precision@4 = 2/4 = 0.5 位置 5(物品 5):不相关,跳过 AP@5 = (0.5 + 0.5) / 2 = 0.5 """ recommended_k = recommended[:k] relevant_set = set (relevant) if len (relevant_set) == 0 : return 0.0 hits = 0 precision_sum = 0.0 for i, item in enumerate (recommended_k, 1 ): if item in relevant_set: hits += 1 precision_at_i = hits / i precision_sum += precision_at_i if hits == 0 : return 0.0 return precision_sum / len (relevant_set) def dcg_at_k (recommended: List [int ], relevant: List [int ], k: int ) -> float : """计算 DCG@K( Discounted Cumulative Gain) DCG 是信息检索中常用的指标,考虑了: 1. 相关性等级(这里简化为 0 或 1) 2. 位置折扣(位置越靠后,折扣越大) 公式: DCG@K = Σ [(2^rel_i - 1) / log2(i+1)] 位置折扣因子 1/log2(i+1): - 位置 1: 1/log2(2) = 1.0 - 位置 2: 1/log2(3) = 0.631 - 位置 3: 1/log2(4) = 0.5 - 位置 4: 1/log2(5) = 0.431 - ...位置越靠后,权重越小 相关性增益 2^rel_i - 1: - rel=0(不相关): 2^0 - 1 = 0 - rel=1(相关): 2^1 - 1 = 1 - rel=2(很相关): 2^2 - 1 = 3 - rel=3(非常相关): 2^3 - 1 = 7 Args: recommended: 推荐列表 relevant: 相关物品列表 k: 只考虑前 K 个推荐 Returns: DCG@K 值 """ recommended_k = recommended[:k] relevant_set = set (relevant) dcg = 0.0 for i, item in enumerate (recommended_k, 1 ): rel = 1 if item in relevant_set else 0 dcg += (2 ** rel - 1 ) / np.log2(i + 1 ) return dcg def ndcg_at_k (recommended: List [int ], relevant: List [int ], k: int ) -> float : """计算 NDCG@K( Normalized DCG) NDCG 是 DCG 的归一化版本,将 DCG 除以理想情况下的 DCG( IDCG)。 公式: NDCG@K = DCG@K / IDCG@K 其中 IDCG@K 是理想情况下的 DCG,即将所有相关物品按相关性降序排列后的 DCG 。 优势: 1. 归一化后的值在[0,1]之间,便于比较 2. 考虑了位置信息和相关性等级 3. 广泛用于搜索引擎和推荐系统评估 取值范围:[0, 1] - 1 表示推荐列表的顺序是最优的 - 0 表示没有推荐任何相关物品 Args: recommended: 推荐列表 relevant: 相关物品列表 k: 只考虑前 K 个推荐 Returns: NDCG@K 值 """ dcg = dcg_at_k(recommended, relevant, k) ideal_relevant = sorted (relevant, reverse=True )[:k] idcg = dcg_at_k(ideal_relevant, relevant, k) if idcg == 0 : return 0.0 return dcg / idcg
评估指标的使用场景 :
Precision 和
Recall :最基础的指标,易于理解,但不考虑位置信息AP :考虑位置,适合评估排序质量NDCG :综合考虑位置和相关性等级,是最全面的指标,推荐使用
在实际应用中,通常需要同时关注多个指标,因为单一指标无法全面反映推荐系统的效果。
评估指标代码深度解读
关键实现细节 :
Precision@K 的边界情况处理 (第 1842-1845 行):
当推荐列表为空时,返回 0.0(没有推荐任何物品,准确率为 0)
使用集合的交集操作 & 快速计算共同元素,时间复杂度
注意 : Precision@K 的分母是
K(推荐数量),而不是相关物品数量
Recall@K 的边界情况处理 (第 1866-1869 行):
当相关物品集合为空时,返回 0.0(没有相关物品,召回率无意义)
注意 : Recall@K 的分母是相关物品数量,而不是 KPrecision 和 Recall 的区别: Precision 关注"推荐的质量", Recall
关注"覆盖的完整性"
AP@K 的位置加权 (第 1905-1911 行):
AP
考虑了推荐列表中的位置信息:相关物品出现在越靠前的位置,贡献越大
对于位置 Precision@i,即到当前位置为止的准确率
最终 AP 是所有相关物品的 Precision@i 的平均值
DCG 的位置折扣机制 (第 1987-1990 行):
位置折扣因子 1/log2(i+1) 确保位置越靠后,权重越小
相关性增益 2^rel - 1
使得相关性等级越高,增益越大(指数增长)
这种设计符合用户行为:用户更关注推荐列表的前几个物品
NDCG 的归一化 (第 2020-2033 行):
NDCG 将 DCG 除以理想 DCG( IDCG),使得结果在 [0, 1] 之间
IDCG 是将所有相关物品按相关性降序排列后的 DCG
归一化使得不同用户、不同推荐列表的 NDCG 值可以比较
设计权衡 :
Precision vs Recall :
Precision
优先 :推荐更准确,但可能遗漏用户喜欢的物品Recall
优先 :覆盖更全面,但可能推荐不相关的物品平衡 :使用 F1 分数:位置信息的考虑 :不考虑位置 : Precision 、 Recall
只关注推荐列表中是否有相关物品,不关心位置考虑位置 : AP 、 NDCG 认为位置越靠前,价值越大选择建议 :对于排序任务,应该使用考虑位置的指标( AP
、 NDCG) 相关性等级的表示 :
二值化 ( 0 或
1):实现简单,但丢失了相关性程度的差异多等级 (
0-5):更准确,但需要更细粒度的标注数据选择建议 :如果有细粒度标注,使用多等级;否则使用二值化
常见问题与解决方案 :
问题
原因
解决方案
Precision 很高但 Recall 很低
推荐列表太短,或只推荐热门物品
增加推荐数量,或优化算法提升覆盖率
Recall 很高但 Precision 很低
推荐了太多不相关的物品
优化算法提升准确率,或使用更严格的过滤规则
NDCG 值很低
相关物品排在后面,或推荐列表质量差
优化排序算法,确保相关物品排在前面
不同用户的指标差异大
用户行为差异大,或数据不平衡
分别计算每个用户的指标,然后取平均( Mean NDCG)
离线指标与在线指标不一致
离线评估无法完全模拟线上环境
结合 A/B 测试,同时关注离线指标和在线指标
性能优化建议 :
计算效率 :
使用集合操作(set)进行交集计算,时间复杂度
使用向量化操作( NumPy)加速批量计算
实际使用示例 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 def evaluate_recommender (model, test_data: Dict [int , List [int ]], k: int = 10 ) -> Dict [str , float ]: """评估推荐模型 Args: model: 训练好的推荐模型(有 recommend 方法) test_data: 测试数据 {user_id: [relevant_item_ids]} k: Top-K 推荐 Returns: 评估指标字典 """ all_precisions = [] all_recalls = [] all_aps = [] all_ndcgs = [] for user_id, relevant_items in test_data.items(): recommendations = model.recommend(user_id, n=k) recommended_items = [item_id for item_id, _ in recommendations] prec = precision_at_k(recommended_items, relevant_items, k) rec = recall_at_k(recommended_items, relevant_items, k) ap = ap_at_k(recommended_items, relevant_items, k) ndcg = ndcg_at_k(recommended_items, relevant_items, k) all_precisions.append(prec) all_recalls.append(rec) all_aps.append(ap) all_ndcgs.append(ndcg) return { 'Precision@K' : np.mean(all_precisions), 'Recall@K' : np.mean(all_recalls), 'MAP@K' : np.mean(all_aps), 'NDCG@K' : np.mean(all_ndcgs) } user_cf = UserCF(k=3 , similarity='cosine' ) user_cf.fit(ratings) test_data = { 1 : [5 ], 2 : [3 , 4 ], } metrics = evaluate_recommender(user_cf, test_data, k=10 ) print ("评估结果:" )for metric_name, value in metrics.items(): print (f" {metric_name} : {value:.4 f} " )
指标选择指南 :
场景
推荐指标
原因
排序任务
NDCG 、 MAP
考虑位置信息,最全面
分类任务
Precision 、 Recall 、 F1
关注准确率和覆盖率
隐式反馈
Precision 、 Recall
只有点击/未点击,无评分等级
显式反馈
NDCG 、 MAP
有评分等级,可以区分相关性程度
多样性评估
需要额外指标
Precision/Recall 无法评估多样性
业务指标
CTR 、 GMV
离线指标与在线指标可能不一致
总结 :评估指标的选择应该根据具体场景和业务目标来决定。没有单一指标能全面反映推荐系统的效果,通常需要组合使用多个指标。同时,离线指标和在线指标可能不一致,需要通过
A/B 测试验证。
更多代码示例
示例 1:矩阵分解( Matrix
Factorization)
矩阵分解是协同过滤的重要扩展,将用户-物品矩阵分解为两个低维矩阵的乘积。
问题背景 :
传统的协同过滤方法( User-CF 、 Item-CF)存在两个核心问题: 1.
数据稀疏性 :用户-物品评分矩阵通常非常稀疏( 99%+
的元素为空),导致难以找到相似用户或相似物品 2.
可扩展性差 :相似度矩阵的计算和存储成本为
矩阵分解通过将高维稀疏矩阵分解为两个低维稠密矩阵的乘积,解决了这两个问题。
解决思路 :
矩阵分解的基本思路:假设用户对物品的评分可以表示为用户潜在特征向量和物品潜在特征向量的内积 。
数学表示: $$
R P Q^T$$
其中: -
预测公式:
其中
设计考虑 :
为什么用低维表示 ?
降维 :从 泛化能力 :低维表示能捕捉用户和物品的本质特征,避免过拟合计算效率 :预测时只需要计算两个 潜在特征的含义 :潜在特征没有明确的语义解释,是模型自动学习的
例如:对于电影推荐,潜在特征可能捕捉"动作程度"、"浪漫程度"、"艺术性"等抽象维度
用户和物品在同一个潜在空间中,相似的用户/物品在潜在空间中距离较近
优化目标 :
最小化预测误差:{(u,i) } (r {ui} - _u _iT) 2 + (|_u|^2
+ |_i|^2)$4. 优化方法 :
随机梯度下降(
SGD) :逐个样本更新参数,速度快,适合大规模数据交替最小二乘(
ALS) :交替固定一个矩阵,优化另一个矩阵,收敛快但内存占用大批量梯度下降 :每次使用所有样本更新,收敛稳定但速度慢
下面我们实现基于 SGD 的矩阵分解算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 import numpy as npfrom scipy.optimize import minimizefrom typing import Dict , List , Tuple class MatrixFactorization : """矩阵分解推荐算法 该类实现了基于随机梯度下降( SGD)的矩阵分解算法,将用户-物品评分矩阵 分解为两个低维矩阵的乘积,从而学习用户和物品的潜在特征表示。 核心优势: 1. 解决数据稀疏性问题:通过低维表示泛化到未观测的评分 2. 计算效率高:预测时间复杂度 O(k),其中 k 是潜在特征维度 3. 可扩展性强:参数量为 O((m+n)× k),远小于原始矩阵的 O(m × n) """ def __init__ (self, n_factors: int = 10 , learning_rate: float = 0.01 , reg: float = 0.01 , n_iterations: int = 100 ): """初始化矩阵分解模型 Args: n_factors: 潜在特征维度 k - 太小(如 k=5):表达能力不足,无法捕捉复杂的用户-物品关系 - 太大(如 k=200):容易过拟合,计算开销大 - 推荐范围: 10-100,通常取 20-50 learning_rate: 学习率( SGD 的步长) - 太大:可能无法收敛,损失函数震荡 - 太小:收敛速度慢,训练时间长 - 推荐范围: 0.001-0.1,通常取 0.01 reg: 正则化系数 λ,防止过拟合 - 控制模型复杂度:λ 越大,模型越简单(参数越小) - 推荐范围: 0.001-0.1,通常取 0.01 n_iterations: 训练迭代次数 - 太少:模型未充分训练,预测不准 - 太多:可能过拟合,训练时间长 - 推荐范围: 50-200,可以通过早停( early stopping)优化 """ self.n_factors = n_factors self.learning_rate = learning_rate self.reg = reg self.n_iterations = n_iterations self.user_factors = None self.item_factors = None def fit (self, ratings: Dict [int , Dict [int , float ]] ): """训练矩阵分解模型 训练流程: 1. 构建用户和物品的索引映射(将原始 ID 映射到连续索引) 2. 初始化用户和物品的潜在特征矩阵(随机初始化) 3. 使用随机梯度下降( SGD)迭代优化,最小化预测误差 时间复杂度: O(iterations × |R| × k),其中 |R| 是评分数量, k 是特征维度 空间复杂度: O((m+n) × k),其中 m 是用户数, n 是物品数 Args: ratings: 用户-物品评分字典 格式:{user_id: {item_id: rating, ...}, ...} 例如:{1: {1: 5, 2: 4}, 2: {1: 4, 3: 5 }} """ users = sorted (set (ratings.keys())) items = set () for user_items in ratings.values(): items.update(user_items.keys()) items = sorted (items) n_users = len (users) n_items = len (items) self.user_to_idx = {u: i for i, u in enumerate (users)} self.idx_to_user = {i: u for u, i in self.user_to_idx.items()} self.item_to_idx = {i: idx for idx, i in enumerate (items)} self.idx_to_item = {idx: i for i, idx in self.item_to_idx.items()} self.user_factors = np.random.normal(0 , 0.1 , (n_users, self.n_factors)) self.item_factors = np.random.normal(0 , 0.1 , (n_items, self.n_factors)) train_data = [] for user_id, items_dict in ratings.items(): user_idx = self.user_to_idx[user_id] for item_id, rating in items_dict.items(): item_idx = self.item_to_idx[item_id] train_data.append((user_idx, item_idx, rating)) for iteration in range (self.n_iterations): np.random.shuffle(train_data) for user_idx, item_idx, rating in train_data: self._update_factors(user_idx, item_idx, rating) def _update_factors (self, user_idx: int , item_idx: int , rating: float ): """使用随机梯度下降更新用户和物品的潜在特征向量 这是矩阵分解的核心:对于每个观测到的评分 r_ui,我们: 1. 计算预测值: r ̂_ui = p_u · q_i^T 2. 计算预测误差: e_ui = r_ui - r ̂_ui 3. 更新用户特征: p_u ← p_u + α(e_ui · q_i - λ · p_u) 4. 更新物品特征: q_i ← q_i + α(e_ui · p_u - λ · q_i) 其中: - α 是学习率( learning_rate) - λ 是正则化系数( reg) - e_ui · q_i 是误差对用户特征的梯度 - e_ui · p_u 是误差对物品特征的梯度 - λ · p_u 和 λ · q_i 是正则化项的梯度 注意:更新物品特征时使用 user_factor_old(更新前的值), 而不是更新后的值,这是 SGD 的标准做法。 Args: user_idx: 用户的索引(不是原始 ID) item_idx: 物品的索引(不是原始 ID) rating: 用户对物品的真实评分 r_ui """ prediction = np.dot(self.user_factors[user_idx], self.item_factors[item_idx]) error = rating - prediction user_factor_old = self.user_factors[user_idx].copy() self.user_factors[user_idx] += self.learning_rate * ( error * self.item_factors[item_idx] - self.reg * self.user_factors[user_idx] ) self.item_factors[item_idx] += self.learning_rate * ( error * user_factor_old - self.reg * self.item_factors[item_idx] ) def predict (self, user_id: int , item_id: int ) -> float : """预测用户对物品的评分 预测公式: r ̂_ui = p_u · q_i^T 时间复杂度: O(k),其中 k 是潜在特征维度 空间复杂度: O(1) Args: user_id: 用户的原始 ID item_id: 物品的原始 ID Returns: 预测评分,范围 [1.0, 5.0] 如果用户或物品不在训练集中,返回默认值 3.0(中等评分) """ if user_id not in self.user_to_idx or item_id not in self.item_to_idx: return 3.0 user_idx = self.user_to_idx[user_id] item_idx = self.item_to_idx[item_id] prediction = np.dot(self.user_factors[user_idx], self.item_factors[item_idx]) return max (1.0 , min (5.0 , prediction)) def recommend (self, user_id: int , n: int = 10 ) -> List [Tuple [int , float ]]: """为用户推荐 Top-N 物品 推荐流程: 1. 获取用户的潜在特征向量 2. 计算用户对所有物品的预测评分(向量化操作,高效) 3. 按预测评分降序排序 4. 返回 Top-N 物品 时间复杂度: O(n_items × k + n_items × log(n_items)) 空间复杂度: O(n_items) Args: user_id: 用户的原始 ID n: 推荐物品数量( Top-N) Returns: 推荐列表:[(item_id, predicted_rating), ...] 按 predicted_rating 降序排列 """ if user_id not in self.user_to_idx: return [] user_idx = self.user_to_idx[user_id] user_vector = self.user_factors[user_idx] predictions = np.dot(self.item_factors, user_vector) item_scores = [(self.idx_to_item[i], score) for i, score in enumerate (predictions)] item_scores.sort(key=lambda x: x[1 ], reverse=True ) return item_scores[:n]
矩阵分解代码深度解读
关键实现细节 :
索引映射的必要性 (第 2208-2221 行):
原始用户 ID 和物品 ID 可能不连续(如 1, 3, 5,
100),直接用作数组索引会浪费大量内存
映射到连续索引( 0, 1, 2, 3)后,可以使用高效的 NumPy 数组操作
优化建议 :对于大规模系统,可以使用哈希表或数据库存储映射关系 随机初始化的选择 (第 2224-2225 行):
使用正态分布 N(0, 0.1)
随机初始化,避免初始值过大或过小
Xavier 初始化 :对于更深层的网络,可以使用
N(0, 1/k) 或 N(0, 2/(k+1))预训练初始化 :如果有其他数据源,可以使用预训练的嵌入向量初始化 SGD 更新规则 (第 2241-2255 行):
关键点 1 :更新物品特征时使用
user_factor_old(更新前的值),这是 SGD 的标准做法关键点 2 :正则化项 λ · p_u 和
λ · q_i 防止参数过大,避免过拟合关键点 3 :学习率 α
控制更新步长,太大可能导致不收敛,太小收敛慢 向量化预测 (第 2277 行):
使用 np.dot(self.item_factors, user_vector)
一次性计算所有物品的预测评分
这比循环调用 predict() 快得多( NumPy
的矩阵乘法经过高度优化)
时间复杂度:
设计权衡 :
SGD vs ALS vs 批量梯度下降 :
SGD (当前实现):速度快,内存占用小,适合大规模数据,但需要调学习率ALS :收敛快,但内存占用大(需要存储中间结果),适合中小规模数据批量梯度下降 :收敛稳定,但速度慢,不适合大规模数据 潜在特征维度 k 的选择 :
k 太小 (如
k=5):表达能力不足,无法捕捉复杂的用户-物品关系k 太大 (如
k=200):容易过拟合,计算开销大,泛化能力差推荐范围 : 10-100,通常取
20-50,可以通过交叉验证选择最优值 正则化系数 λ 的选择 :
λ 太小 :模型容易过拟合,参数值可能过大λ
太大 :模型欠拟合,参数值被过度压缩,预测能力下降推荐范围 : 0.001-0.1,通常取
0.01,可以通过交叉验证选择
常见问题与解决方案 :
问题
原因
解决方案
预测评分都是中等值( 3.0 左右)
模型未充分训练,或学习率太小
增加迭代次数,或增大学习率
训练损失不下降
学习率太大,或初始化不当
减小学习率,使用更小的初始化标准差
过拟合(训练集效果好,测试集效果差)
正则化系数太小,或特征维度太大
增大正则化系数,或减小特征维度
训练速度慢
迭代次数太多,或数据量太大
使用早停( early stopping),或采样训练数据
内存占用过大
特征维度太大,或用户/物品数太多
减小特征维度,或使用稀疏矩阵存储
性能优化建议 :
大规模系统优化 :
分布式训练 :使用 Spark MLlib 或 TensorFlow
的分布式训练增量更新 :当新用户/物品加入时,只更新相关参数,而非重新训练特征缓存 :缓存用户和物品的特征向量,避免重复计算 实际使用示例 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 from sklearn.model_selection import train_test_splitratings = { 1 : {1 : 5 , 2 : 4 , 3 : 3 , 4 : 5 }, 2 : {1 : 4 , 2 : 5 , 3 : 4 , 5 : 3 }, 3 : {2 : 3 , 3 : 5 , 4 : 4 , 5 : 5 }, 4 : {1 : 3 , 3 : 4 , 4 : 3 , 5 : 4 }, 5 : {2 : 5 , 4 : 5 , 5 : 4 } } mf = MatrixFactorization( n_factors=10 , learning_rate=0.01 , reg=0.01 , n_iterations=100 ) mf.fit(ratings) predicted_rating = mf.predict(user_id=1 , item_id=5 ) print (f"用户 1 对物品 5 的预测评分: {predicted_rating:.2 f} " )recommendations = mf.recommend(user_id=1 , n=5 ) print ("\n 推荐结果:" )for item_id, score in recommendations: print (f" 物品 {item_id} : 预测评分 {score:.2 f} " ) print (f"\n 用户 1 的潜在特征向量: {mf.user_factors[mf.user_to_idx[1 ]]} " )print (f"物品 5 的潜在特征向量: {mf.item_factors[mf.item_to_idx[5 ]]} " )
与协同过滤的对比 :
特性
User-CF / Item-CF
矩阵分解
数据稀疏性 需要足够的共同评分,稀疏时效果差
通过低维表示泛化,对稀疏数据更鲁棒 ⭐
可扩展性 相似度矩阵
参数量
可解释性 高("相似用户也喜欢")
低(潜在特征无明确语义)
计算效率 预测需要查找相似用户/物品
预测只需向量内积
冷启动 新用户/物品难以处理
可以通过其他特征初始化 ⭐
总结 :矩阵分解是协同过滤的重要扩展,通过低维表示解决了数据稀疏性和可扩展性问题。虽然可解释性不如传统协同过滤,但在大规模系统中表现更好,是现代推荐系统的基础方法。
示例 2:内容推荐实现
内容推荐( Content-Based
Recommendation)是推荐系统的另一大范式,与协同过滤不同,它基于物品的内容特征而非用户行为数据。
问题背景 :
协同过滤方法存在一个根本性问题:冷启动 。当新用户或新物品加入系统时,由于缺乏历史行为数据,无法进行推荐。内容推荐通过分析物品的内容特征(文本、标签、类别等)来解决这个问题。
解决思路 :
内容推荐的基本思路:如果用户喜欢某些物品,那么具有相似内容特征的其他物品也应该被推荐 。
算法流程: 1.
物品特征提取 :从物品内容中提取特征向量(如 TF-IDF
、词向量等) 2.
用户画像构建 :基于用户历史喜欢的物品,构建用户偏好向量(加权平均)
3. 相似度计算 :计算候选物品与用户画像的相似度 4.
生成推荐 :按相似度排序,取 Top-N
设计考虑 :
为什么用 TF-IDF ?
TF(词频) :衡量词语在文档中的重要性IDF(逆文档频率) :衡量词语的区分度(常见词权重低,罕见词权重高)TF-IDF :结合两者,既能捕捉文档特征,又能区分不同文档 用户画像的构建 :
使用加权平均:用户对物品的评分越高,该物品的特征对用户画像的贡献越大
公式:
相似度度量 :
使用余弦相似度:衡量用户画像向量和物品特征向量的夹角
余弦相似度只关注方向,不关注大小,适合处理不同长度的文本
下面我们实现完整的内容推荐算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 from sklearn.feature_extraction.text import TfidfVectorizerfrom sklearn.metrics.pairwise import cosine_similarityimport numpy as npfrom typing import Dict , List , Tuple , Set class ContentBased : """基于内容的推荐算法 该类实现了完整的内容推荐流程,包括: 1. 使用 TF-IDF 提取物品的文本特征 2. 基于用户历史评分构建用户画像(加权平均) 3. 使用余弦相似度计算物品与用户画像的相似度 4. 生成 Top-N 推荐 优势: - 可以处理冷启动问题(新用户、新物品) - 推荐结果可解释性强("因为物品包含关键词 X") - 不依赖用户行为数据,适合内容丰富的场景 局限性: - 需要高质量的内容特征 - 可能陷入"信息茧房"(只推荐相似内容) - 无法发现用户的潜在兴趣 """ def __init__ (self, max_features: int = 1000 ): """初始化内容推荐模型 Args: max_features: TF-IDF 的最大特征数(词汇表大小) - 太小:表达能力不足,可能丢失重要特征 - 太大:计算开销大,可能引入噪声 - 推荐范围: 500-5000,通常取 1000-2000 """ self.vectorizer = TfidfVectorizer(max_features=max_features) self.item_features = None self.user_profiles = {} self.item_ids = [] def fit (self, items: Dict [int , str ], ratings: Dict [int , Dict [int , float ]] ): """训练内容推荐模型 训练流程: 1. 提取物品特征:使用 TF-IDF 将物品文本转换为特征向量 2. 构建用户画像:基于用户历史评分,计算加权平均特征向量 时间复杂度: O(n_items × avg_text_length + n_users × avg_items_per_user × n_features) 空间复杂度: O(n_items × n_features + n_users × n_features) Args: items: 物品 ID 到文本内容的映射 例如:{1: "action movie with car chase", 2: "romantic comedy"} ratings: 用户-物品评分字典 格式:{user_id: {item_id: rating, ...}, ...} """ self.item_ids = list (items.keys()) item_texts = [items[item_id] for item_id in self.item_ids] self.item_features = self.vectorizer.fit_transform(item_texts) for user_id, user_ratings in ratings.items(): profile = np.zeros(self.item_features.shape[1 ]) total_weight = 0.0 for item_id, rating in user_ratings.items(): if item_id in self.item_ids: item_idx = self.item_ids.index(item_id) item_vector = self.item_features[item_idx].toarray()[0 ] profile += rating * item_vector total_weight += rating if total_weight > 0 : profile /= total_weight self.user_profiles[user_id] = profile def recommend (self, user_id: int , n: int = 10 , exclude_items: Set [int ] = None ) -> List [Tuple [int , float ]]: """为用户推荐 Top-N 物品 推荐流程: 1. 获取用户的画像向量 2. 计算用户画像与所有物品特征的余弦相似度 3. 过滤已排除的物品(如用户已评分的物品) 4. 按相似度降序排序,返回 Top-N 时间复杂度: O(n_items × n_features) 空间复杂度: O(n_items) Args: user_id: 目标用户 ID n: 推荐物品数量( Top-N) exclude_items: 需要排除的物品集合(如用户已评分的物品) Returns: 推荐列表:[(item_id, similarity_score), ...] 按 similarity_score 降序排列 """ if user_id not in self.user_profiles: return [] user_profile = self.user_profiles[user_id].reshape(1 , -1 ) similarities = cosine_similarity(user_profile, self.item_features)[0 ] results = [] exclude_items = exclude_items or set () for item_id, similarity in zip (self.item_ids, similarities): if item_id not in exclude_items: results.append((item_id, similarity)) results.sort(key=lambda x: x[1 ], reverse=True ) return results[:n]
内容推荐代码深度解读
关键实现细节 :
TF-IDF 特征提取 (第 2317 行):
TF-IDF 将文本转换为数值向量,捕捉词语的重要性
TF(词频) :IDF(逆文档频率) :TF-IDF :用户画像的加权平均 (第 2324-2332 行):使用评分作为权重:用户对物品的评分越高,该物品的特征对用户画像的贡献越大
归一化:除以总权重,确保用户画像不受评分数量影响
优势 :比简单平均更能反映用户的真实偏好 余弦相似度计算 (第 2357 行):
余弦相似度衡量两个向量的夹角,范围 [-1, 1]
只关注方向,不关注大小,适合处理不同长度的文本
公式:设计权衡 :
TF-IDF vs Word2Vec vs BERT :
TF-IDF (当前实现):简单快速,适合短文本,但无法捕捉语义Word2Vec :能捕捉词语的语义相似性,但需要预训练模型BERT :最强大,能捕捉深层语义,但计算开销大 用户画像构建方法 :
加权平均 (当前实现):考虑评分权重,更准确简单平均 :不考虑评分差异,计算简单但不够准确时间衰减 :给最近的行为更高权重,适合兴趣变化的场景
常见问题与解决方案 :
问题
原因
解决方案
推荐结果过于相似
只考虑内容特征,陷入"信息茧房"
结合协同过滤,增加多样性
新用户无推荐
新用户没有历史评分,无法构建画像
使用注册信息或热门物品作为初始推荐
特征维度太高
max_features 太大,计算慢
减小 max_features,或使用特征选择
文本质量差
物品描述不准确或不完整
使用多源特征(标签、类别、图像等)
实际使用示例 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 items = { 1 : "action thriller car chase explosion" , 2 : "romantic comedy love story happy ending" , 3 : "sci-fi space adventure future" , 4 : "horror scary ghost mystery" , 5 : "action adventure hero save world" } ratings = { 1 : {1 : 5 , 5 : 4 }, 2 : {2 : 5 , 3 : 4 }, } cb = ContentBased(max_features=1000 ) cb.fit(items, ratings) recommendations = cb.recommend( user_id=1 , n=3 , exclude_items={1 , 5 } ) print ("推荐结果:" )for item_id, score in recommendations: print (f" 物品 {item_id} : 相似度 {score:.3 f} " ) print (f" 内容: {items[item_id]} " )
与协同过滤的对比 :
特性
协同过滤
内容推荐
数据需求 用户行为数据
物品内容特征 ⭐
冷启动 新用户/物品难以处理
可以处理新用户/物品 ⭐
可解释性 中等("相似用户也喜欢")
高("因为物品包含特征 X") ⭐
多样性 可以发现潜在兴趣
可能陷入"信息茧房"
适用场景 用户行为丰富
内容特征丰富 ⭐
总结 :内容推荐通过分析物品内容特征解决了冷启动问题,推荐结果可解释性强。但可能陷入"信息茧房",通常与协同过滤结合使用(混合推荐)。
示例 3:评估框架
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 class RecommendationEvaluator : """推荐系统评估器""" def __init__ (self, test_data: Dict [int , List [int ]] ): """ Args: test_data: 测试数据 {user_id: [relevant_item_ids]} """ self.test_data = test_data def evaluate (self, recommendations: Dict [int , List [int ]], metrics: List [str ] = ['precision' , 'recall' , 'ndcg' ], k: int = 10 ) -> Dict [str , float ]: """评估推荐结果 Args: recommendations: 推荐结果 {user_id: [recommended_item_ids]} metrics: 要计算的指标列表 k: Top-K """ results = {} if 'precision' in metrics: results['precision' ] = self._mean_precision(recommendations, k) if 'recall' in metrics: results['recall' ] = self._mean_recall(recommendations, k) if 'ndcg' in metrics: results['ndcg' ] = self._mean_ndcg(recommendations, k) if 'map' in metrics: results['map' ] = self._mean_ap(recommendations, k) return results def _mean_precision (self, recommendations: Dict [int , List [int ]], k: int ) -> float : """计算平均 Precision@K""" precisions = [] for user_id, recommended in recommendations.items(): if user_id in self.test_data: relevant = self.test_data[user_id] prec = precision_at_k(recommended, relevant, k) precisions.append(prec) return np.mean(precisions) if precisions else 0.0 def _mean_recall (self, recommendations: Dict [int , List [int ]], k: int ) -> float : """计算平均 Recall@K""" recalls = [] for user_id, recommended in recommendations.items(): if user_id in self.test_data: relevant = self.test_data[user_id] rec = recall_at_k(recommended, relevant, k) recalls.append(rec) return np.mean(recalls) if recalls else 0.0 def _mean_ndcg (self, recommendations: Dict [int , List [int ]], k: int ) -> float : """计算平均 NDCG@K""" ndcgs = [] for user_id, recommended in recommendations.items(): if user_id in self.test_data: relevant = self.test_data[user_id] ndcg = ndcg_at_k(recommended, relevant, k) ndcgs.append(ndcg) return np.mean(ndcgs) if ndcgs else 0.0 def _mean_ap (self, recommendations: Dict [int , List [int ]], k: int ) -> float : """计算平均 AP@K""" aps = [] for user_id, recommended in recommendations.items(): if user_id in self.test_data: relevant = self.test_data[user_id] ap = ap_at_k(recommended, relevant, k) aps.append(ap) return np.mean(aps) if aps else 0.0
示例 4:处理稀疏性的技巧
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 def jaccard_similarity (set1: set , set2: set ) -> float : """计算 Jaccard 相似度(适用于隐式反馈)""" intersection = len (set1 & set2) union = len (set1 | set2) return intersection / union if union > 0 else 0.0 def normalize_ratings (ratings: Dict [int , Dict [int , float ]] ) -> Dict [int , Dict [int , float ]]: """归一化评分(减去用户平均评分)""" normalized = {} user_avgs = {} for user_id, items in ratings.items(): user_avgs[user_id] = np.mean(list (items.values())) for user_id, items in ratings.items(): normalized[user_id] = { item_id: rating - user_avgs[user_id] for item_id, rating in items.items() } return normalized def implicit_feedback_to_ratings (clicks: Dict [int , List [int ]], threshold: int = 1 ) -> Dict [int , Dict [int , float ]]: """将隐式反馈(点击)转换为评分""" ratings = {} for user_id, clicked_items in clicks.items(): item_counts = defaultdict(int ) for item_id in clicked_items: item_counts[item_id] += 1 ratings[user_id] = { item_id: min (5.0 , 1.0 + count * 0.5 ) for item_id, count in item_counts.items() if count >= threshold } return ratings
示例 5:多样性优化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 def diversify_recommendations (recommendations: List [Tuple [int , float ]], item_categories: Dict [int , str ], max_same_category: int = 2 ) -> List [Tuple [int , float ]]: """增加推荐结果的多样性""" diversified = [] category_counts = defaultdict(int ) for item_id, score in recommendations: category = item_categories.get(item_id, 'unknown' ) if category_counts[category] < max_same_category: diversified.append((item_id, score)) category_counts[category] += 1 if len (diversified) >= len (recommendations): break return diversified def mmr_rerank (candidates: List [Tuple [int , float ]], item_features: np.ndarray, lambda_param: float = 0.5 , n: int = 10 ) -> List [int ]: """使用 MMR (Maximal Marginal Relevance) 重排序""" if len (candidates) == 0 : return [] selected = [] remaining = candidates.copy() first_item, first_score = remaining.pop(0 ) selected.append(first_item) while len (selected) < n and len (remaining) > 0 : best_score = -float ('inf' ) best_idx = -1 for idx, (item_id, rel_score) in enumerate (remaining): max_sim = 0.0 item_feature = item_features[item_id] for selected_item in selected: selected_feature = item_features[selected_item] sim = cosine_similarity([item_feature], [selected_feature])[0 ][0 ] max_sim = max (max_sim, sim) mmr_score = lambda_param * rel_score - (1 - lambda_param) * max_sim if mmr_score > best_score: best_score = mmr_score best_idx = idx if best_idx >= 0 : selected_item, _ = remaining.pop(best_idx) selected.append(selected_item) return selected
示例 6:冷启动处理
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class ColdStartHandler : """冷启动处理""" def __init__ (self, popular_items: List [int ], item_features: Dict [int , np.ndarray] = None ): self.popular_items = popular_items self.item_features = item_features def recommend_for_new_user (self, user_info: Dict [str , any ], n: int = 10 ) -> List [int ]: """为新用户推荐""" if len (self.popular_items) >= n: return self.popular_items[:n] if self.item_features and 'interests' in user_info: interests = user_info['interests' ] return self.popular_items[:n] return self.popular_items[:n] def recommend_for_new_item (self, item_features: np.ndarray, user_profiles: Dict [int , np.ndarray], n: int = 10 ) -> List [int ]: """为新物品推荐用户""" if not user_profiles: return [] similarities = [] for user_id, profile in user_profiles.items(): sim = cosine_similarity([item_features], [profile])[0 ][0 ] similarities.append((user_id, sim)) similarities.sort(key=lambda x: x[1 ], reverse=True ) return [user_id for user_id, _ in similarities[:n]]
示例 7:实时推荐更新
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class OnlineRecommender : """在线推荐系统(支持实时更新)""" def __init__ (self, base_model ): self.base_model = base_model self.user_recent_actions = defaultdict(list ) self.item_popularity = defaultdict(int ) def update_user_action (self, user_id: int , item_id: int , action_type: str ): """更新用户行为""" self.user_recent_actions[user_id].append({ 'item_id' : item_id, 'action_type' : action_type, 'timestamp' : time.time() }) self.item_popularity[item_id] += 1 if len (self.user_recent_actions[user_id]) > 100 : self.user_recent_actions[user_id] = \ self.user_recent_actions[user_id][-100 :] def recommend_with_realtime (self, user_id: int , n: int = 10 ) -> List [int ]: """结合实时行为的推荐""" base_recs = self.base_model.recommend(user_id, n * 2 ) recent_items = [action['item_id' ] for action in self.user_recent_actions[user_id][-10 :]] boosted_recs = [] for item_id, score in base_recs: boost = 1.0 for recent_item in recent_items: if self._are_similar(item_id, recent_item): boost *= 1.2 boosted_recs.append((item_id, score * boost)) boosted_recs.sort(key=lambda x: x[1 ], reverse=True ) return [item_id for item_id, _ in boosted_recs[:n]] def _are_similar (self, item1: int , item2: int ) -> bool : """判断两个物品是否相似(简化实现)""" return False
示例 8: A/B 测试框架
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class ABTestFramework : """A/B 测试框架""" def __init__ (self ): self.experiments = {} self.results = defaultdict(list ) def create_experiment (self, name: str , variants: Dict [str , any ] ): """创建实验""" self.experiments[name] = variants def assign_user (self, user_id: int , experiment_name: str ) -> str : """为用户分配实验组""" hash_val = hash (str (user_id) + experiment_name) % 100 variants = list (self.experiments[experiment_name].keys()) variant_idx = hash_val % len (variants) return variants[variant_idx] def log_result (self, experiment_name: str , variant: str , metric: str , value: float ): """记录实验结果""" key = (experiment_name, variant, metric) self.results[key].append(value) def get_statistics (self, experiment_name: str , metric: str ) -> Dict : """获取实验统计结果""" stats = {} for (exp, variant, met), values in self.results.items(): if exp == experiment_name and met == metric: stats[variant] = { 'mean' : np.mean(values), 'std' : np.std(values), 'count' : len (values) } return stats
示例 9:特征工程工具
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 class FeatureEngineer : """特征工程工具类""" def __init__ (self ): self.feature_stats = {} self.scalers = {} def compute_user_statistics (self, ratings: Dict [int , Dict [int , float ]], window_days: int = 30 ) -> Dict [int , Dict ]: """计算用户统计特征""" import datetime from collections import defaultdict user_stats = defaultdict(lambda : { 'total_ratings' : 0 , 'avg_rating' : 0.0 , 'rating_std' : 0.0 , 'recent_ratings' : 0 , 'active_days' : set () }) current_time = datetime.datetime.now() for user_id, items in ratings.items(): ratings_list = list (items.values()) user_stats[user_id]['total_ratings' ] = len (ratings_list) user_stats[user_id]['avg_rating' ] = np.mean(ratings_list) user_stats[user_id]['rating_std' ] = np.std(ratings_list) user_stats[user_id]['recent_ratings' ] = len (ratings_list) user_stats[user_id]['active_days' ] = len (set ()) return dict (user_stats) def compute_item_statistics (self, ratings: Dict [int , Dict [int , float ]] ) -> Dict [int , Dict ]: """计算物品统计特征""" from collections import defaultdict item_stats = defaultdict(lambda : { 'total_ratings' : 0 , 'avg_rating' : 0.0 , 'rating_std' : 0.0 , 'popularity' : 0.0 }) item_users = defaultdict(list ) for user_id, items in ratings.items(): for item_id, rating in items.items(): item_users[item_id].append((user_id, rating)) for item_id, user_ratings in item_users.items(): ratings_list = [r for _, r in user_ratings] item_stats[item_id]['total_ratings' ] = len (ratings_list) item_stats[item_id]['avg_rating' ] = np.mean(ratings_list) item_stats[item_id]['rating_std' ] = np.std(ratings_list) item_stats[item_id]['popularity' ] = len (user_ratings) return dict (item_stats) def normalize_features (self, features: np.ndarray, method: str = 'standard' ) -> np.ndarray: """特征归一化""" from sklearn.preprocessing import StandardScaler, MinMaxScaler if method == 'standard' : scaler = StandardScaler() elif method == 'minmax' : scaler = MinMaxScaler() else : raise ValueError(f"Unknown normalization method: {method} " ) normalized = scaler.fit_transform(features) return normalized
示例 10:批量预测优化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class BatchPredictor : """批量预测优化器""" def __init__ (self, model, batch_size: int = 100 ): self.model = model self.batch_size = batch_size def predict_batch (self, user_ids: List [int ], item_ids: List [int ] ) -> List [float ]: """批量预测,提高效率""" predictions = [] for i in range (0 , len (user_ids), self.batch_size): batch_users = user_ids[i:i+self.batch_size] batch_items = item_ids[i:i+self.batch_size] batch_preds = [] for user_id, item_id in zip (batch_users, batch_items): pred = self.model.predict(user_id, item_id) batch_preds.append(pred) predictions.extend(batch_preds) return predictions def recommend_batch (self, user_ids: List [int ], n: int = 10 ) -> Dict [int , List [Tuple [int , float ]]]: """批量推荐""" results = {} for user_id in user_ids: recs = self.model.recommend(user_id, n) results[user_id] = recs return results
示例 11:推荐结果缓存
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 from functools import lru_cacheimport timeclass CachedRecommender : """带缓存的推荐器""" def __init__ (self, base_model, cache_ttl: int = 3600 ): self.base_model = base_model self.cache_ttl = cache_ttl self.cache = {} self.cache_times = {} def _is_cache_valid (self, key: str ) -> bool : """检查缓存是否有效""" if key not in self.cache: return False cache_time = self.cache_times.get(key, 0 ) return (time.time() - cache_time) < self.cache_ttl def recommend (self, user_id: int , n: int = 10 ) -> List [Tuple [int , float ]]: """带缓存的推荐""" cache_key = f"user_{user_id} _n_{n} " if self._is_cache_valid(cache_key): return self.cache[cache_key] recommendations = self.base_model.recommend(user_id, n) self.cache[cache_key] = recommendations self.cache_times[cache_key] = time.time() return recommendations def invalidate_cache (self, user_id: int = None ): """清除缓存""" if user_id is None : self.cache.clear() self.cache_times.clear() else : keys_to_remove = [k for k in self.cache.keys() if f"user_{user_id} " in k] for key in keys_to_remove: del self.cache[key] del self.cache_times[key]
示例 12:推荐结果解释
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 class ExplainableRecommender : """可解释的推荐器""" def __init__ (self, base_model ): self.base_model = base_model def explain_recommendation (self, user_id: int , item_id: int , method: str = 'item_cf' ) -> Dict [str , any ]: """解释推荐理由""" explanation = { 'item_id' : item_id, 'predicted_rating' : self.base_model.predict(user_id, item_id), 'reasons' : [] } if method == 'item_cf' and hasattr (self.base_model, 'item_similarity' ): user_items = self.base_model.ratings.get(user_id, {}) similar_items = [] for rated_item in user_items.keys(): sim_key = (item_id, rated_item) if sim_key in self.base_model.item_similarity: sim = self.base_model.item_similarity[sim_key] rating = user_items[rated_item] similar_items.append({ 'item_id' : rated_item, 'similarity' : sim, 'user_rating' : rating }) similar_items.sort(key=lambda x: x['similarity' ], reverse=True ) explanation['reasons' ] = [ f"因为你喜欢物品 {item['item_id' ]} (评分 {item['user_rating' ]} )," f"而该物品与推荐物品相似度为 {item['similarity' ]:.2 f} " for item in similar_items[:3 ] ] elif method == 'user_cf' and hasattr (self.base_model, 'user_similarity' ): similar_users = [] for other_user in self.base_model.ratings.keys(): if other_user == user_id: continue if item_id not in self.base_model.ratings.get(other_user, {}): continue sim_key = (user_id, other_user) if sim_key in self.base_model.user_similarity: sim = self.base_model.user_similarity[sim_key] rating = self.base_model.ratings[other_user][item_id] similar_users.append({ 'user_id' : other_user, 'similarity' : sim, 'rating' : rating }) similar_users.sort(key=lambda x: x['similarity' ], reverse=True ) explanation['reasons' ] = [ f"相似用户 {user['user_id' ]} 也喜欢该物品(评分 {user['rating' ]} )," f"你们相似度为 {user['similarity' ]:.2 f} " for user in similar_users[:3 ] ] return explanation
示例 13:推荐系统性能分析
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 import timeimport cProfileimport pstatsclass PerformanceAnalyzer : """性能分析器""" def __init__ (self ): self.metrics = defaultdict(list ) def time_function (self, func, *args, **kwargs ): """计时函数执行""" start_time = time.time() result = func(*args, **kwargs) end_time = time.time() execution_time = end_time - start_time self.metrics[func.__name__].append(execution_time) return result, execution_time def profile_function (self, func, *args, **kwargs ): """性能分析""" profiler = cProfile.Profile() profiler.enable() result = func(*args, **kwargs) profiler.disable() stats = pstats.Stats(profiler) stats.sort_stats('cumulative' ) stats.print_stats(10 ) return result def get_statistics (self, func_name: str ) -> Dict : """获取统计信息""" if func_name not in self.metrics: return {} times = self.metrics[func_name] return { 'mean' : np.mean(times), 'std' : np.std(times), 'min' : np.min (times), 'max' : np.max (times), 'count' : len (times) }
示例 14:推荐系统可视化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 import matplotlib.pyplot as pltimport seaborn as snsclass RecommendationVisualizer : """推荐系统可视化工具""" def plot_user_similarity_matrix (self, user_similarity: Dict [Tuple [int , int ], float ], user_ids: List [int ] ): """绘制用户相似度矩阵""" n_users = len (user_ids) similarity_matrix = np.zeros((n_users, n_users)) user_to_idx = {u: i for i, u in enumerate (user_ids)} for (u1, u2), sim in user_similarity.items(): if u1 in user_to_idx and u2 in user_to_idx: i1, i2 = user_to_idx[u1], user_to_idx[u2] similarity_matrix[i1, i2] = sim plt.figure(figsize=(10 , 8 )) sns.heatmap(similarity_matrix, annot=True , fmt='.2f' , cmap='YlOrRd' ) plt.title('User Similarity Matrix' ) plt.xlabel('User ID' ) plt.ylabel('User ID' ) plt.show() def plot_recommendation_distribution (self, recommendations: Dict [int , List [Tuple [int , float ]]] ): """绘制推荐分数分布""" all_scores = [] for recs in recommendations.values(): scores = [score for _, score in recs] all_scores.extend(scores) plt.figure(figsize=(10 , 6 )) plt.hist(all_scores, bins=50 , edgecolor='black' ) plt.xlabel('Predicted Rating' ) plt.ylabel('Frequency' ) plt.title('Distribution of Predicted Ratings' ) plt.show() def plot_coverage_over_time (self, recommendations_history: List [Dict [int , List [int ]]] ): """绘制覆盖率随时间的变化""" coverage_history = [] all_items = set () for recs in recommendations_history: items = set () for item_list in recs.values(): items.update(item_list) all_items.update(items) coverage_history.append(len (items)) plt.figure(figsize=(10 , 6 )) plt.plot(coverage_history) plt.xlabel('Time Step' ) plt.ylabel('Number of Unique Items Recommended' ) plt.title('Coverage Over Time' ) plt.show()
常见问题解答( Q&A)
Q1:
协同过滤和内容推荐有什么区别?什么时候用哪个?
A :
协同过滤基于用户行为数据,不需要物品内容信息,但需要足够的用户-物品交互数据。内容推荐基于物品特征,可以处理冷启动问题,但需要提取有效的物品特征。
选择建议 : -
如果有丰富的用户行为数据,优先使用协同过滤(特别是 Item-CF) -
如果物品有丰富的文本/标签特征,且用户行为数据稀疏,使用内容推荐 -
最佳实践是混合使用两种方法
Q2: User-CF 和 Item-CF
哪个更好?
A : 在大多数场景下, Item-CF 表现更好,原因: 1.
物品相似度比用户相似度更稳定(物品特征变化慢) 2.
物品数量通常少于用户数量,计算效率更高 3. 可解释性更好("因为你喜欢
A,所以推荐 B")
但 User-CF 也有优势: - 能发现用户潜在兴趣(通过相似用户) -
对用户兴趣变化更敏感
Q3:
推荐系统如何解决数据稀疏性问题?
A : 主要方法: 1.
矩阵分解 :将稀疏矩阵分解为低维稠密矩阵 2.
隐式反馈 :利用点击、浏览时长等数据,数据量远大于显式评分
3. 内容特征 :结合物品内容特征,补充协同过滤 4.
深度学习 :使用神经网络学习用户和物品的表示
Q4: 如何评估推荐系统的效果?
A : 需要多维度评估: - 准确率指标 :
Precision 、 Recall 、 NDCG 、 MAP -
多样性指标 :类别多样性、平均成对距离 -
覆盖率指标 :物品覆盖率、长尾覆盖率 -
新颖性指标 :平均流行度倒数 -
业务指标 : CTR 、 GMV 、用户留存等
没有单一指标能全面反映效果,需要组合使用。
Q5:
推荐系统如何处理冷启动问题?
A : 分两种情况:
新用户冷启动 : - 收集注册信息(年龄、性别、地域等)
- 推荐热门物品 - 让用户选择兴趣标签 - 使用内容推荐
新物品冷启动 : - 使用内容特征(文本、图片、标签) -
给予新物品曝光机会(探索机制) - 使用多臂老虎机算法
Q6:
为什么推荐系统需要多阶段架构(召回-粗排-精排-重排)?
A : 这是效果和效率的平衡: -
召回层 :从百万级物品中快速召回数千个候选(毫秒级) -
粗排层 :用简单模型快速筛选到数百个(百毫秒级) -
精排层 :用复杂模型精确排序到数十个(可接受延迟) -
重排层 :考虑业务规则和多样性
如果只用精排模型处理所有物品,计算量太大,无法满足实时性要求。
Q7: 推荐系统如何保证多样性?
A : 方法包括: 1.
多样性约束 :在排序时加入多样性项 2.
类别打散 :避免连续推荐相同类别 3. MMR
算法 :平衡相关性和多样性 4.
重排层规则 :在最终推荐列表中保证多样性
Q8:
深度学习在推荐系统中如何应用?
A : 深度学习主要用于精排层: -
Wide&Deep :结合线性模型和深度神经网络 -
DeepFM :自动学习特征交叉 -
DIN :使用注意力机制建模用户兴趣 -
BERT :用于文本特征提取
深度学习的优势是能自动学习特征交互,但需要大量数据和计算资源。
Q9:
推荐系统如何平衡准确率和多样性?
A : 这是一个权衡问题: -
准确率优先 :可能推荐过于同质化,用户容易疲劳 -
多样性优先 :可能推荐不相关的内容,用户体验下降
常用方法: 1. 多目标优化 :同时优化准确率和多样性 2.
重排策略 :先按准确率排序,再在重排层保证多样性 3.
探索-利用平衡 :在推荐准确内容的同时,探索用户可能感兴趣的新内容
Q10:
推荐系统如何应对用户兴趣变化?
A : 方法包括: 1.
时间衰减 :给最近的行为更高权重 2.
实时更新 :实时更新用户特征和推荐结果 3.
短期/长期兴趣分离 :分别建模用户的短期和长期兴趣 4.
在线学习 :模型在线更新,无需重新训练
Q11:
推荐系统的可解释性重要吗?如何实现?
A : 可解释性很重要: - 增加用户信任 -
帮助用户理解推荐逻辑 - 便于调试和优化
实现方法: 1. 可解释模型 :使用 Item-CF
等可解释的算法 2.
推荐理由 :提供"相似用户也喜欢"、"基于你的浏览历史"等理由
3. 注意力可视化 :使用注意力机制可视化模型关注的特征
Q12:
推荐系统如何处理公平性问题?
A : 公平性是一个重要但容易被忽视的问题: 1.
公平性约束 :在优化目标中加入公平性项 2.
数据平衡 :确保训练数据的多样性 3.
定期审计 :监控推荐结果的公平性 4.
去偏见算法 :使用去偏见的推荐算法
Q13:
推荐系统如何评估离线效果和在线效果的一致性?
A : 离线指标和在线指标可能不一致: -
离线指标 : Precision 、 Recall 、 NDCG 等 -
在线指标 : CTR 、 GMV 、用户留存等
方法: 1. A/B 测试 :在线上对比不同算法 2.
相关性分析 :分析离线指标和在线指标的相关性 3.
模拟环境 :构建模拟环境,更接近线上情况
Q14:
推荐系统的计算复杂度如何优化?
A : 优化方法: 1.
多阶段架构 :召回-粗排-精排-重排 2.
缓存 :缓存热门结果和用户特征 3.
近似算法 :使用 LSH 、 ANN 等近似最近邻算法 4.
分布式计算 :使用 Spark 、 Flink 等分布式框架 5.
模型压缩 :模型量化、剪枝等
Q15:
推荐系统如何处理多目标优化(如 CTR 和 GMV)?
A : 多目标优化方法: 1.
加权求和 :将多个目标加权平均 2. Pareto
优化 :寻找 Pareto 最优解 3.
多任务学习 :同时优化多个目标 4.
业务规则 :在不同场景下调整目标权重
总结
推荐系统是一个复杂而有趣的领域,涉及算法、工程、产品等多个方面。本文介绍了推荐系统的基础概念、主流方法、评估指标、系统架构和核心挑战,并提供了完整的代码实现。
关键要点 : 1.
推荐系统三大范式:协同过滤、内容推荐、混合推荐 2.
评估需要多维度:准确率、多样性、覆盖率、新颖性 3.
工业级系统采用多阶段架构:召回-粗排-精排-重排 4.
核心挑战:冷启动、稀疏性、长尾、可解释性、实时性、公平性 5. 基础算法:
User-CF 、 Item-CF 、矩阵分解
下一步学习方向 : - 深度学习推荐模型( Wide&Deep
、 DeepFM 、 DIN 等) - 序列推荐( RNN 、 Transformer) -
强化学习在推荐中的应用 - 推荐系统的工程实践(特征工程、模型服务、 A/B
测试)
推荐系统是一个不断发展的领域,新的算法和技术层出不穷。但无论技术如何变化,核心目标始终不变:理解用户,推荐他们真正感兴趣的内容 。