强化学习（六）—— PPO 与 TRPO：信任域策略优化
Chen Kai BOSS
  2024-09-03 14:30:00 2024-09-03 14:30      8.9k 字  36 分钟  

在第三章中，我们介绍了策略梯度方法的基本原理：通过采样轨迹计算梯度，直接优化策略参数。然而， vanilla 策略梯度存在一个根本性问题——更新不稳定。一次过大的策略更新可能导致性能急剧下降，而且由于策略已经改变，很难从错误中恢复。这就像在悬崖边走钢丝：一步走错，满盘皆输。

信任域方法（ Trust Region Methods）的核心思想是：限制每次策略更新的幅度，确保新策略不会偏离旧策略太远。 TRPO（ Trust Region Policy Optimization）通过 KL 散度约束实现这一目标，而 PPO（ Proximal Policy Optimization）则用更简单的裁剪机制达到类似效果。 PPO 因其实现简单、性能稳定，已成为当今应用最广泛的强化学习算法——从 OpenAI Five 到 ChatGPT 的 RLHF， PPO 无处不在。

本章将从策略梯度的不稳定性问题出发，深入剖析信任域方法的理论基础，详解 TRPO 的数学推导和自然梯度的几何直觉，然后介绍 PPO 如何用简单的裁剪机制近似 TRPO 的效果。我们还将探讨这些算法在实践中的技巧和在 RLHF 中的应用。

策略梯度的不稳定性问题

Vanilla Policy Gradient 回顾

让我们先回顾策略梯度的核心思想。策略梯度方法直接参数化策略，目标是最大化期望回报：

$$

J() = {}[R()] = {}$$

通过 REINFORCE 算法，我们可以得到梯度的无偏估计：

其中 是从时刻 开始的折扣回报。这个公式的直觉是：如果一个动作序列获得了高回报，就增加采取这些动作的概率；反之则降低。

引入基线（ baseline） 后，我们通常使用优势函数 代替，这样可以降低方差同时保持无偏性：

为什么策略更新不稳定？

策略梯度看起来简洁优美，但在实践中却经常遇到训练不稳定的问题。让我们通过一个具体例子来理解这个问题。

例子：动作概率的剧烈变化

假设当前策略在某个状态 下选择动作 的概率是 0.9，选择 的概率是 0.1 。在一次采样中，我们恰好采样到了动作，并且这个轨迹获得了很高的回报。

策略梯度会做什么？它会大幅增加 的概率！但问题是：

  1. 高方差：由于 被采样的概率很低（只有 0.1），这样的"好运"轨迹非常罕见。大部分时候我们采样到的是，即使 的回报一般，梯度也会指向增加 的概率。这导致梯度估计的方差非常大。

  2. 分布漂移（ Distribution Shift）：一旦我们更新了策略，新策略 与旧策略 的数据分布就不同了。但我们用来计算梯度的数据是从旧策略采集的！这意味着我们的梯度估计可能在新策略下完全不准确。

  3. 性能塌陷（ Performance Collapse）：一次过大的更新可能将策略推向一个非常糟糕的区域。比如，如果我们把 的概率从 0.1 提升到 0.8，但 实际上只是因为运气好才获得了高回报，那么新策略的性能会急剧下降。更糟糕的是，由于数据分布已经改变，我们很难从这个错误中恢复。

数学分析：步长的影响

考虑策略参数的梯度更新：。

对目标函数做泰勒展开：

$$

J(') J() + (' - )^T _J() + (' - )^T H (' - )$$

其中 是 Hessian 矩阵。代入：

$$

J(') J() + ||J()||^2 + J()^T H _J()$$

如果步长 太大，二阶项 可能变得很大。如果 有负特征值（目标函数非凸），这一项可能是负的，导致——性能下降了！

参数空间 vs 策略空间

更深层的问题是：参数空间的欧氏距离并不能反映策略的真实变化程度。

考虑两个高斯策略： - ，方差很小 - ，方差很大

这两个策略可能只有一个参数（方差）不同，在参数空间中距离很近。但它们的行为完全不同！ 几乎确定性地选择附近的动作，而 的动作几乎是随机的。

这告诉我们：我们不应该在参数空间中限制更新步长，而应该在策略分布空间中限制更新幅度。这正是信任域方法的核心思想。

一个形象的类比

想象你在一个陌生的山区徒步。你的目标是到达山顶（最大化回报）。

Vanilla Policy Gradient就像这样：你看了一眼指南针（梯度方向），然后朝那个方向走一大步。问题是： - 你可能走到悬崖边 - 你可能掉进深坑 - 一旦走错，很难回头

Trust Region Methods更谨慎：你确保每一步都不会走太远，始终待在"安全区域"内。即使方向稍有偏差，你也不会陷入危险。

重要性采样与策略优化

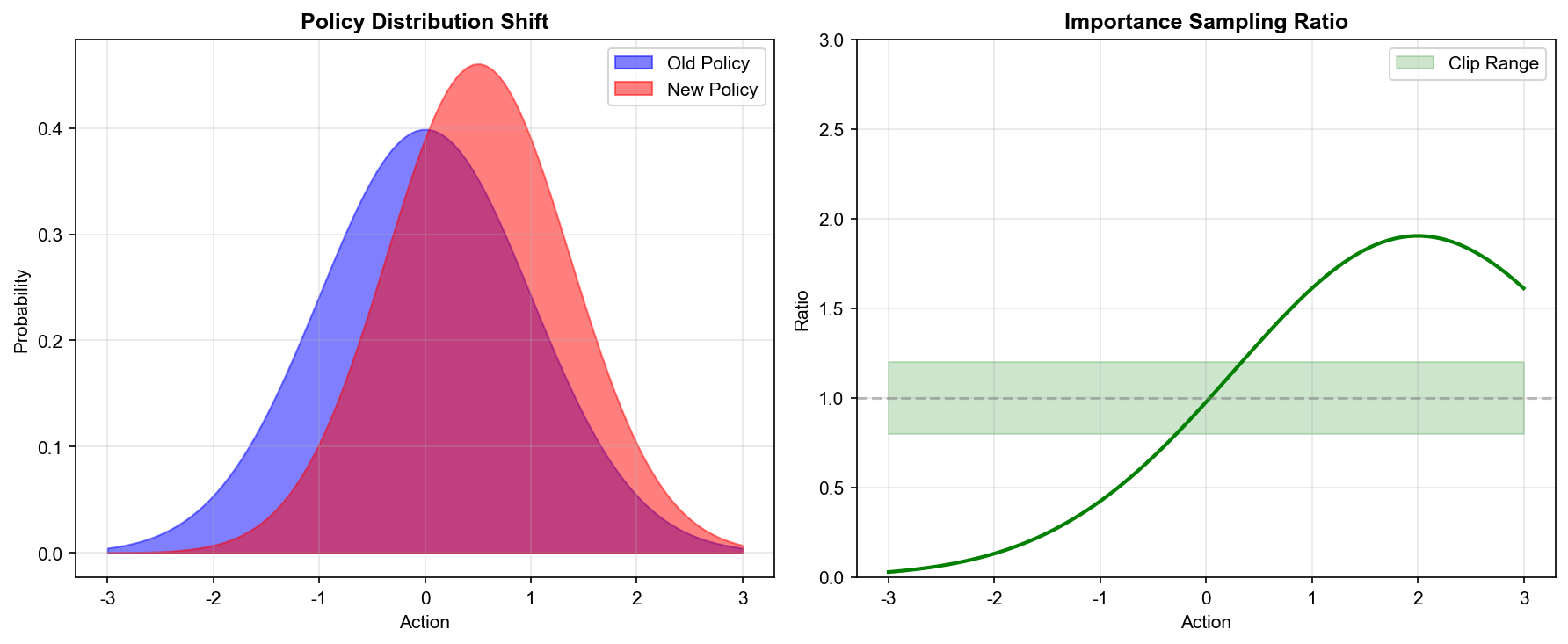
重要性采样：重用旧数据

在策略梯度中，每次更新策略后，旧数据就"过时"了——它们是从旧策略采集的，分布与新策略不同。这导致样本效率很低：我们需要不断采集新数据。

重要性采样（ Importance Sampling）提供了一种重用旧数据的方法。基本思想是：如果我们想计算分布 下的期望，但只有分布 的样本，可以通过加权来修正：

权重 叫做重要性权重，它修正了分布的差异。

应用到策略优化

假设我们有旧策略采集的轨迹数据，现在想评估新策略 的性能。应用重要性采样：

$$

J() = {{_{old}}}$$

其中轨迹 的概率比为：

注意到初始状态分布 和转移概率 在分子分母中相同，可以约掉：

这是一个关键结果：轨迹的重要性权重只取决于策略的动作概率比，与环境动态无关！

代理目标函数

直接优化 仍然有问题：轨迹的重要性权重是所有时间步权重的乘积，当 很大时，这个乘积的方差会指数增长。

一个更实用的方法是定义代理目标函数（ Surrogate Objective），只考虑单步的重要性权重：

$$

L^{CPI}() = {s,a {_{old}}}$$

其中 是旧策略的优势函数。我们通常简写为：

$$

L^{CPI}() = _t$$

其中 是概率比。

代理目标函数的关键性质：

  1. 一阶近似：在 处， 与真实目标 有相同的梯度：

  1. 值相等：在 处，，所以。

这意味着代理目标函数是真实目标函数的一个良好局部近似！但问题是：当 远离 时，这个近似可能完全失效。

重要性采样的方差问题

当新旧策略差异较大时，重要性权重的方差会急剧增大。考虑权重的期望和方差：

期望总是 1，很好。但方差呢？

如果某个动作 在新策略下概率很高（）但在旧策略下概率很低（），则权重，权重的平方是 81！这会导致：

  1. 梯度估计的方差爆炸
  2. 少数高权重样本主导整个梯度
  3. 训练极不稳定

这就是为什么我们需要限制新旧策略的差异——这正是信任域方法的核心。

TRPO：信任域策略优化

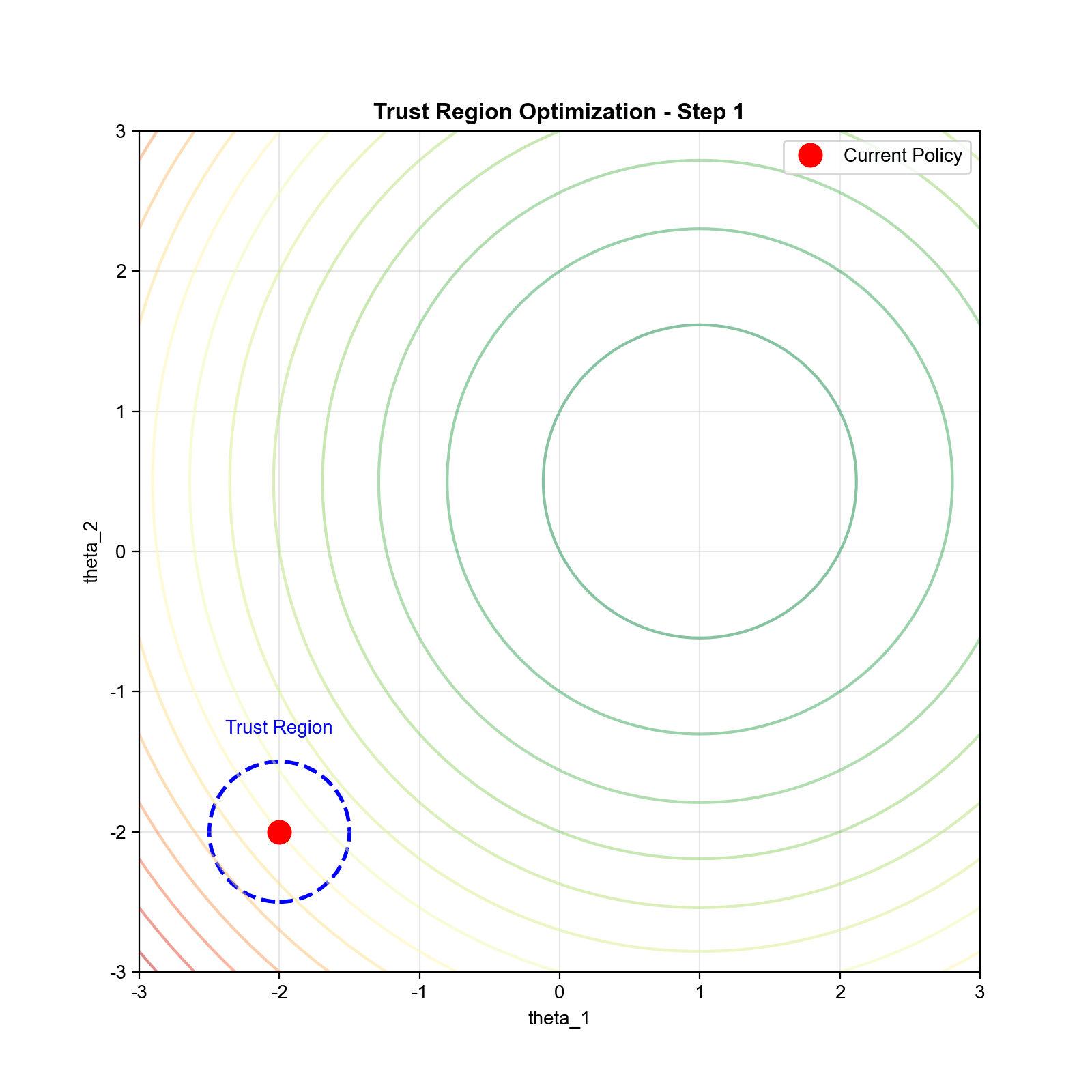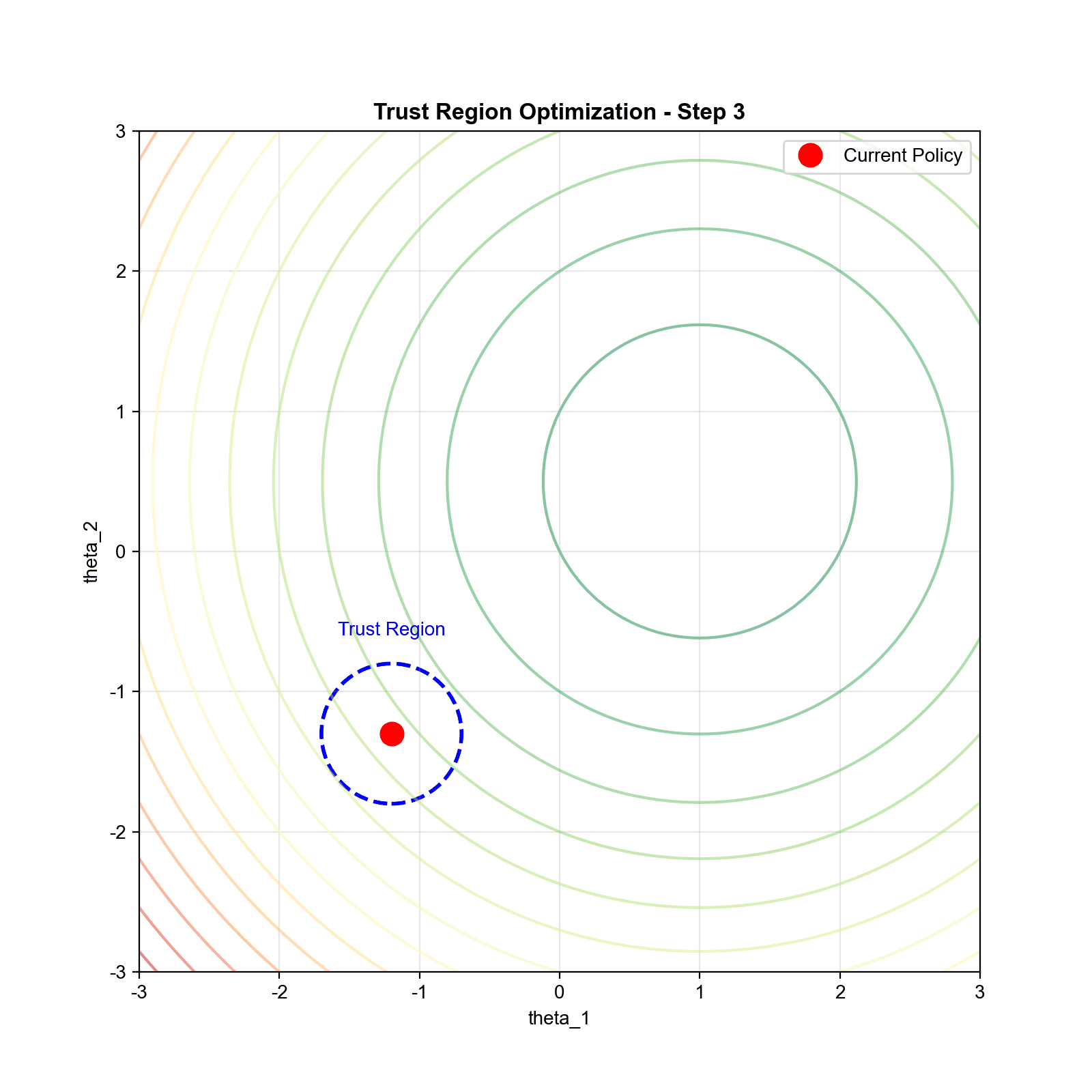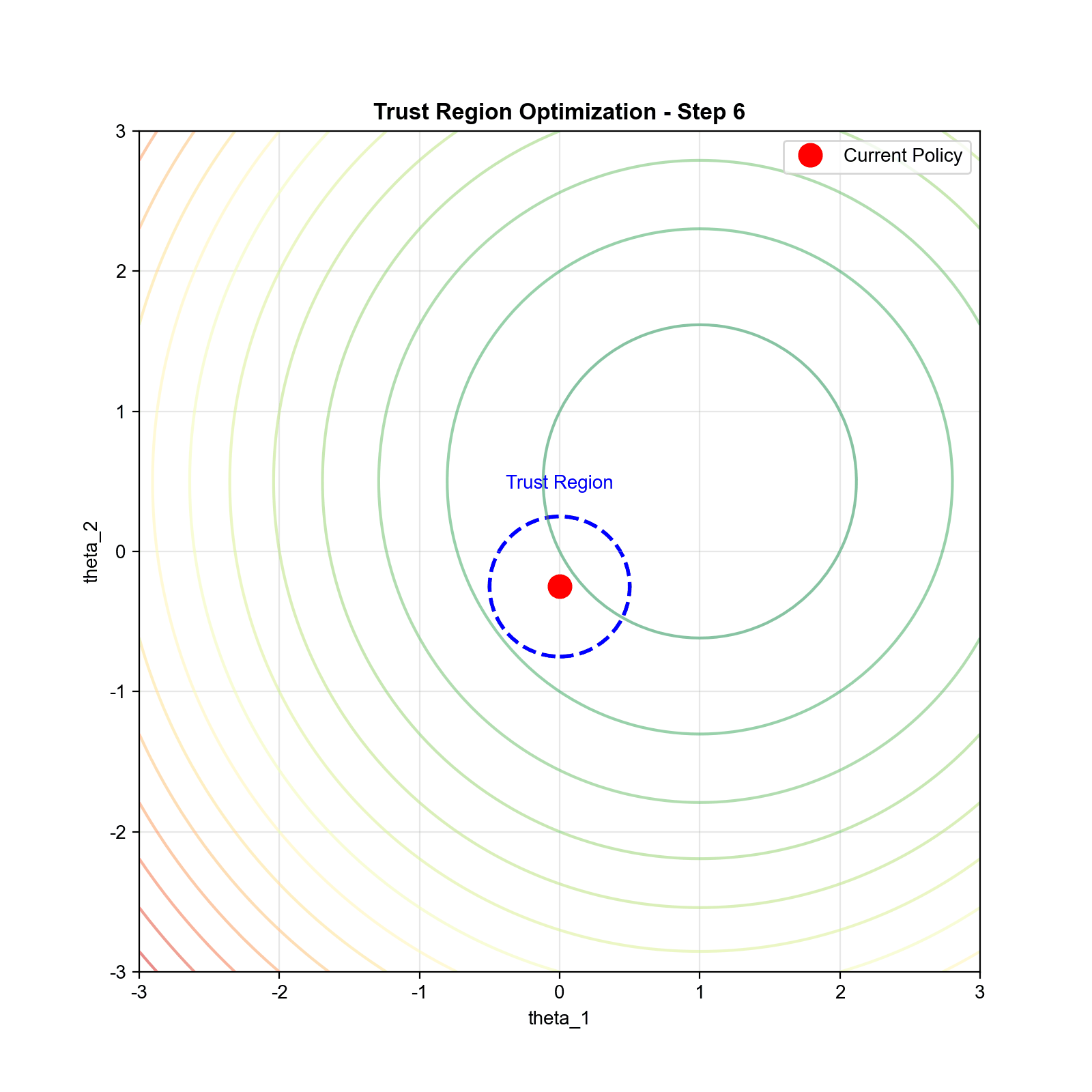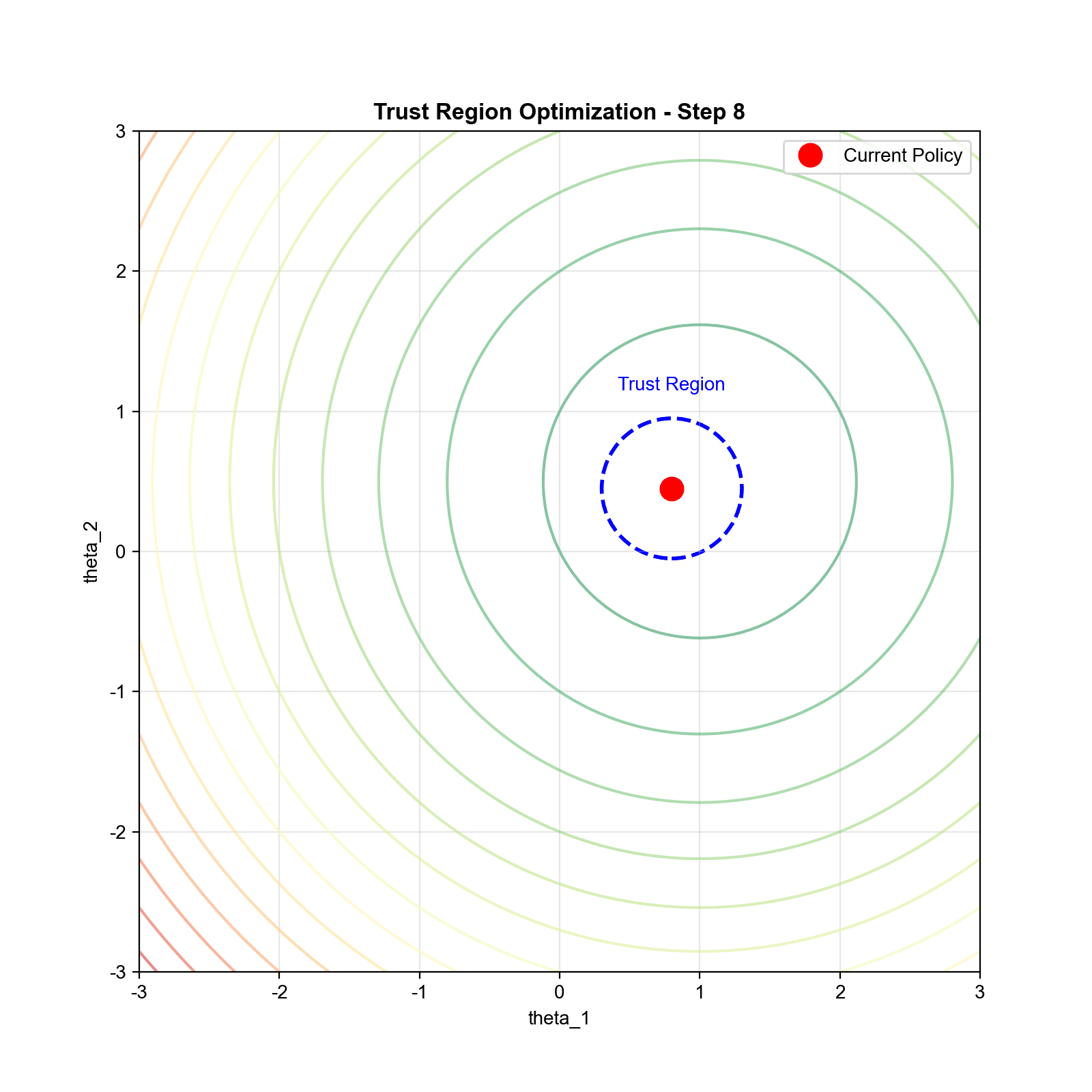
理论基础：策略改进下界

TRPO 的理论基础来自 Kakade 和 Langford (2002)的一个重要结果。

定义策略 的期望回报：

定理：新策略 的期望回报可以表示为：

其中 是旧策略 的优势函数。

证明思路：

利用 的关系，以及 telescope sum 技巧，可以得到：

这个定理告诉我们：新策略的性能等于旧策略的性能加上一个"优势项"。如果我们能让新策略在每个状态下都选择正优势的动作，性能就会提升！

从精确等式到可优化的近似

上面的等式看起来很美，但有一个问题：右边的期望是在 下计算的，而我们还没有！这是一个鸡生蛋的问题。

近似 1：用旧策略的状态分布

定义在旧策略状态分布下的代理目标：

$$

L_(') = () + s (s) a '(a|s) A(s,a)$$

其中 是旧策略的折扣状态访问频率。

这个 可以用旧策略的数据估计：

$$

L_(') = () + {s , a '}$$

用重要性采样把 换成：

$$

L_(') = () + {s , a }$$

关键问题： 和真实目标 差多远？

策略改进的保守下界

Schulman et al. (2015) 证明了一个关键定理：

定理（策略改进下界）：

其中： - 是优势函数的最大绝对值 - 是最大总变差距离 - 是总变差距离

由于总变差距离和 KL 散度的关系：，我们得到：

其中。

这个定理的意义：

它给出了新策略性能的一个保守下界。只要我们： 1. 最大化代理目标$L_(')同时限制散度D_{KL}^{}(|| ')$ 不要太大

就能保证新策略 的性能至少不会比旧策略差太多！这就是信任域方法的理论基础。

TRPO 的优化问题

基于上述理论， TRPO 将策略优化形式化为约束优化问题：

其中 是信任域大小，通常取 0.01 左右。

注意：我们用平均 KL 散度 代替了最大 KL 散度。这是一个实用的近似——最大 KL 散度在实践中很难计算和优化。

自然梯度：策略空间的几何

要理解 TRPO 的优化方法，我们需要先理解自然梯度的概念。

问题：参数空间的欧氏距离有什么问题？

考虑标准梯度下降：。这等价于求解：

最后一项 是参数空间的欧氏距离约束。但正如我们之前讨论的，参数空间的欧氏距离不能反映策略的真实变化。

自然梯度的思想

自然梯度不在参数空间中做约束，而是在概率分布空间中做约束。具体来说，我们用 KL 散度来衡量策略的变化：

$

当 接近 时， KL 散度可以用泰勒展开近似：

$$

D_{KL}(|| {'}) (' - )^T F (' - )$$

其中 是Fisher 信息矩阵：

$$

F = {s , a }$$

Fisher 矩阵定义了策略空间的黎曼度量，它告诉我们在每个参数点，策略分布对参数变化有多敏感。

自然梯度的形式

用拉格朗日乘数法求解上述约束优化问题，可以得到自然梯度更新：

其中 就是自然梯度。

直觉理解：

普通梯度在参数空间中指向"最陡"的方向。但如果参数空间的坐标系选得不好（某些方向对策略影响大，某些方向影响小），这个方向可能不是提升性能最快的。

自然梯度通过 Fisher 矩阵"校正"了这个问题。它在策略分布空间中找到最陡的方向，然后映射回参数空间。这就像在地球上导航：虽然经纬度是正交坐标，但在不同纬度，一度经度对应的实际距离是不同的。自然梯度考虑了这种"度量的变化"。

TRPO 的具体实现

TRPO 使用共轭梯度法（ Conjugate Gradient）高效求解约束优化问题，避免显式计算和存储。

算法步骤：

  1. 收集数据：用当前策略采集轨迹
  2. 估计优势：计算每个状态-动作对的优势（通常用 GAE）
  3. 计算策略梯度：$g = L()|{_{old}}用共轭梯度求解：x = F^{-1}g$ - 不需要显式计算，只需要计算（矩阵-向量乘积）
    • 可以用一次前向和反向传播高效计算
  4. 计算步长：（使得 KL 约束刚好满足）
  5. 回溯线搜索：找到满足约束且确实提升目标的最大步长
  6. 更新参数： 共轭梯度法的核心

共轭梯度法求解，只需要能计算 即可。 Fisher 矩阵-向量乘积可以高效计算：

$$

Fv = _$$

这需要两次反向传播，但不需要存储整个 矩阵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
import torch
import torch.nn as nn
import numpy as np
from torch.distributions import Categorical, Normal

class TRPOAgent:
    def __init__(self, state_dim, action_dim, hidden_dim=64, delta=0.01, 
                 gamma=0.99, lam=0.95, continuous=False):
        self.continuous = continuous
        self.delta = delta
        self.gamma = gamma
        self.lam = lam
        
        # 策略网络
        if continuous:
            self.policy_mean = nn.Sequential(
                nn.Linear(state_dim, hidden_dim),
                nn.Tanh(),
                nn.Linear(hidden_dim, hidden_dim),
                nn.Tanh(),
                nn.Linear(hidden_dim, action_dim)
            )
            self.policy_log_std = nn.Parameter(torch.zeros(action_dim))
        else:
            self.policy = nn.Sequential(
                nn.Linear(state_dim, hidden_dim),
                nn.Tanh(),
                nn.Linear(hidden_dim, hidden_dim),
                nn.Tanh(),
                nn.Linear(hidden_dim, action_dim),
                nn.Softmax(dim=-1)
            )
        
        # 价值网络
        self.value = nn.Sequential(
            nn.Linear(state_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, 1)
        )
        self.value_optimizer = torch.optim.Adam(self.value.parameters(), lr=1e-3)
    
    def get_policy_params(self):
        """获取策略网络的参数"""
        if self.continuous:
            return list(self.policy_mean.parameters()) + [self.policy_log_std]
        else:
            return list(self.policy.parameters())
    
    def get_action_and_log_prob(self, state):
        """获取动作和对数概率"""
        state = torch.FloatTensor(state)
        if self.continuous:
            mean = self.policy_mean(state)
            std = torch.exp(self.policy_log_std)
            dist = Normal(mean, std)
            action = dist.sample()
            log_prob = dist.log_prob(action).sum()
            return action.detach().numpy(), log_prob.detach()
        else:
            probs = self.policy(state)
            dist = Categorical(probs)
            action = dist.sample()
            return action.item(), dist.log_prob(action).detach()
    
    def compute_advantages(self, rewards, values, dones):
        """计算 GAE 优势估计"""
        advantages = []
        gae = 0
        for t in reversed(range(len(rewards))):
            if t == len(rewards) - 1:
                next_value = 0
            else:
                next_value = values[t+1]
            delta = rewards[t] + self.gamma * next_value * (1 - dones[t]) - values[t]
            gae = delta + self.gamma * self.lam * (1 - dones[t]) * gae
            advantages.insert(0, gae)
        return torch.FloatTensor(advantages)
    
    def flat_grad(self, grads):
        """将梯度展平为一维向量"""
        return torch.cat([g.view(-1) for g in grads if g is not None])
    
    def flat_params(self):
        """将参数展平为一维向量"""
        params = self.get_policy_params()
        return torch.cat([p.view(-1) for p in params])
    
    def set_flat_params(self, flat_params):
        """从一维向量恢复参数"""
        params = self.get_policy_params()
        idx = 0
        for p in params:
            p.data.copy_(flat_params[idx:idx+p.numel()].view(p.shape))
            idx += p.numel()
    
    def compute_kl(self, states):
        """计算新旧策略的 KL 散度"""
        if self.continuous:
            mean = self.policy_mean(states)
            std = torch.exp(self.policy_log_std)
            mean_old = mean.detach()
            std_old = std.detach()
            
            # KL(old || new) for Gaussian
            kl = (torch.log(std/std_old) + (std_old**2 + (mean_old-mean)**2)/(2*std**2) - 0.5).sum(dim=1).mean()
        else:
            probs = self.policy(states)
            probs_old = probs.detach()
            kl = (probs_old * (torch.log(probs_old + 1e-8) - torch.log(probs + 1e-8))).sum(dim=1).mean()
        return kl
    
    def hessian_vector_product(self, states, vector, damping=0.1):
        """计算 Fisher 矩阵与向量的乘积: Fv"""
        kl = self.compute_kl(states)
        
        params = self.get_policy_params()
        grads = torch.autograd.grad(kl, params, create_graph=True)
        flat_grads = self.flat_grad(grads)
        
        grad_vector_product = (flat_grads * vector).sum()
        hv = torch.autograd.grad(grad_vector_product, params)
        flat_hv = self.flat_grad(hv)
        
        return flat_hv + damping * vector
    
    def conjugate_gradient(self, states, b, n_steps=10, residual_tol=1e-10):
        """共轭梯度法求解 Fx = b"""
        x = torch.zeros_like(b)
        r = b.clone()
        p = r.clone()
        rdotr = r.dot(r)
        
        for _ in range(n_steps):
            Ap = self.hessian_vector_product(states, p)
            alpha = rdotr / (p.dot(Ap) + 1e-8)
            x += alpha * p
            r -= alpha * Ap
            new_rdotr = r.dot(r)
            if new_rdotr < residual_tol:
                break
            p = r + (new_rdotr / rdotr) * p
            rdotr = new_rdotr
        
        return x
    
    def compute_surrogate_loss(self, states, actions, advantages):
        """计算代理目标函数"""
        if self.continuous:
            mean = self.policy_mean(states)
            std = torch.exp(self.policy_log_std)
            dist = Normal(mean, std)
            log_probs = dist.log_prob(actions).sum(dim=1)
        else:
            probs = self.policy(states)
            dist = Categorical(probs)
            log_probs = dist.log_prob(actions)
        
        # 这里简化了，实际应该用重要性权重
        return (log_probs * advantages).mean()
    
    def line_search(self, states, actions, advantages, step_direction, max_kl):
        """回溯线搜索找到满足约束的最大步长"""
        old_params = self.flat_params().clone()
        old_loss = self.compute_surrogate_loss(states, actions, advantages).item()
        
        # 计算最大步长（使 KL 约束刚好满足）
        sAs = 0.5 * step_direction.dot(self.hessian_vector_product(states, step_direction))
        max_step = torch.sqrt(max_kl / (sAs + 1e-8))
        
        # 回溯线搜索
        for shrink_factor in [0.5 ** i for i in range(10)]:
            step = max_step * shrink_factor
            new_params = old_params + step * step_direction
            self.set_flat_params(new_params)
            
            # 检查 KL 约束
            kl = self.compute_kl(states)
            
            # 检查目标函数是否提升
            new_loss = self.compute_surrogate_loss(states, actions, advantages).item()
            
            if kl.item() < max_kl and new_loss > old_loss:
                return True
        
        # 回退到旧参数
        self.set_flat_params(old_params)
        return False
    
    def update(self, states, actions, rewards, dones):
        """TRPO 更新"""
        states = torch.FloatTensor(np.array(states))
        if self.continuous:
            actions = torch.FloatTensor(np.array(actions))
        else:
            actions = torch.LongTensor(actions)
        
        # 计算价值和优势
        with torch.no_grad():
            values = self.value(states).squeeze().numpy()
        advantages = self.compute_advantages(rewards, values, dones)
        advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)
        
        # 计算策略梯度
        loss = self.compute_surrogate_loss(states, actions, advantages)
        params = self.get_policy_params()
        grads = torch.autograd.grad(loss, params)
        flat_grads = self.flat_grad(grads)
        
        # 共轭梯度求解自然梯度方向
        step_direction = self.conjugate_gradient(states, flat_grads)
        
        # 线搜索
        success = self.line_search(states, actions, advantages, step_direction, self.delta)
        
        # 更新价值函数
        returns = advantages + torch.FloatTensor(values)
        for _ in range(10):
            value_pred = self.value(states).squeeze()
            value_loss = ((value_pred - returns) ** 2).mean()
            self.value_optimizer.zero_grad()
            value_loss.backward()
            self.value_optimizer.step()
        
        return loss.item(), success

TRPO 的优缺点

优点： 1. 理论保证：有明确的性能改进下界 2. 稳定更新： KL 约束确保每次更新不会太激进 3. 样本效率：可以多次重用同一批数据（在 KL 约束内）

缺点： 1. 实现复杂：需要共轭梯度、线搜索 2. 计算昂贵：每次更新需要多次反向传播 3. 调参困难：信任域大小 的选择需要经验

PPO：近端策略优化

从 TRPO 到 PPO 的动机

TRPO 虽然理论优美，但实现复杂，计算昂贵。 Schulman 等人在 2017 年提出了 PPO，目标是：用一阶优化方法近似 TRPO 的效果，同时保持实现简单。

PPO 的核心思想：既然我们想限制新旧策略的差异，为什么不直接在目标函数中加入这个约束？

PPO-Clip：裁剪版本

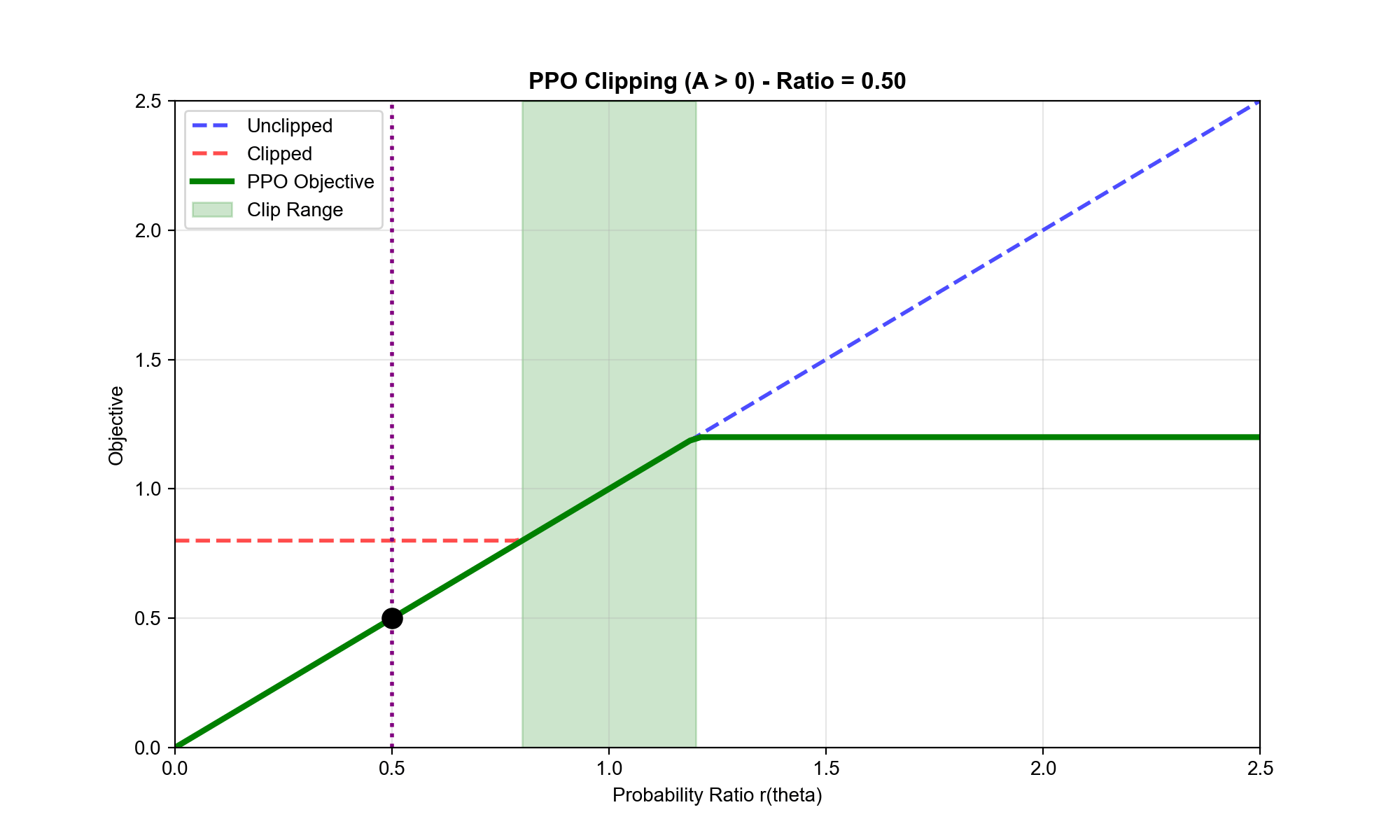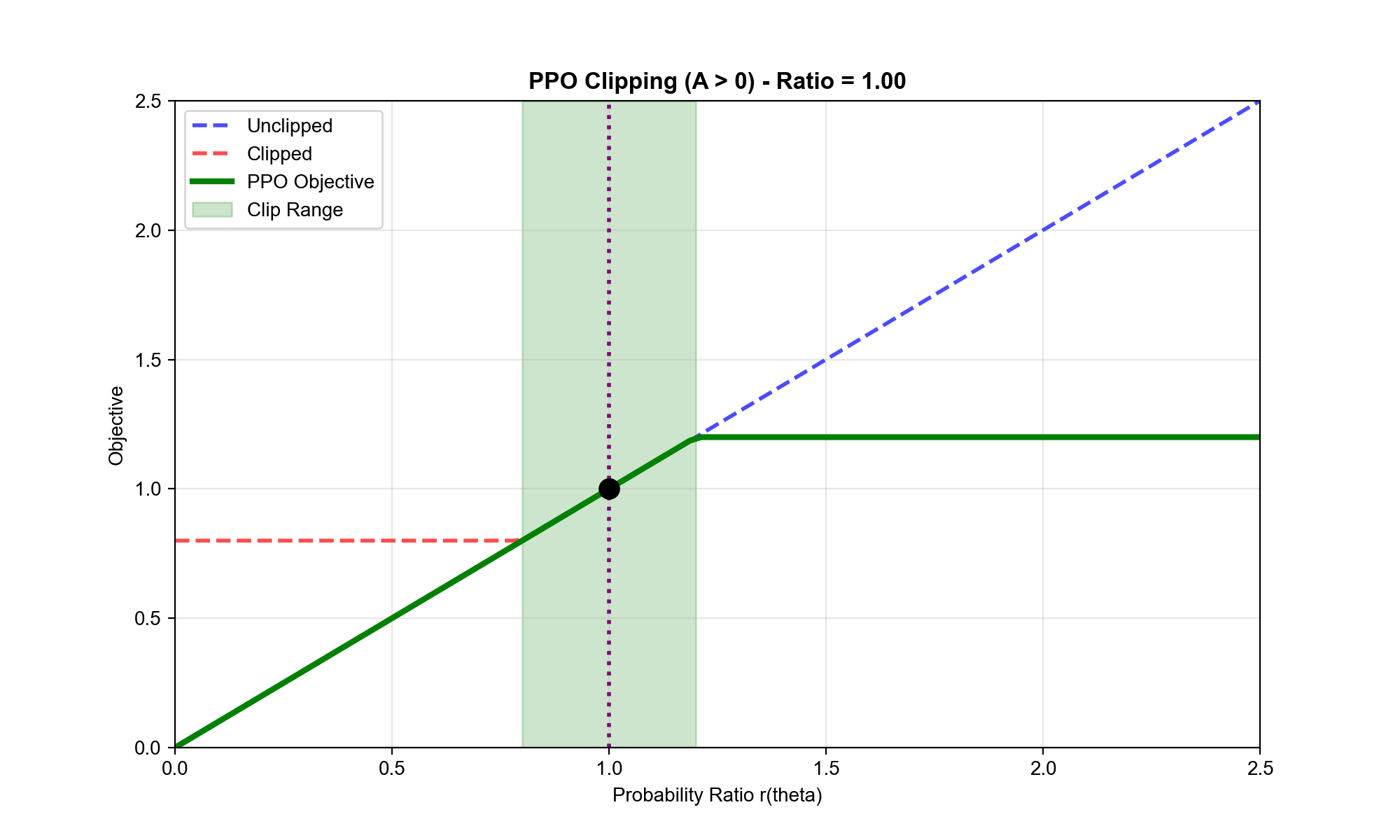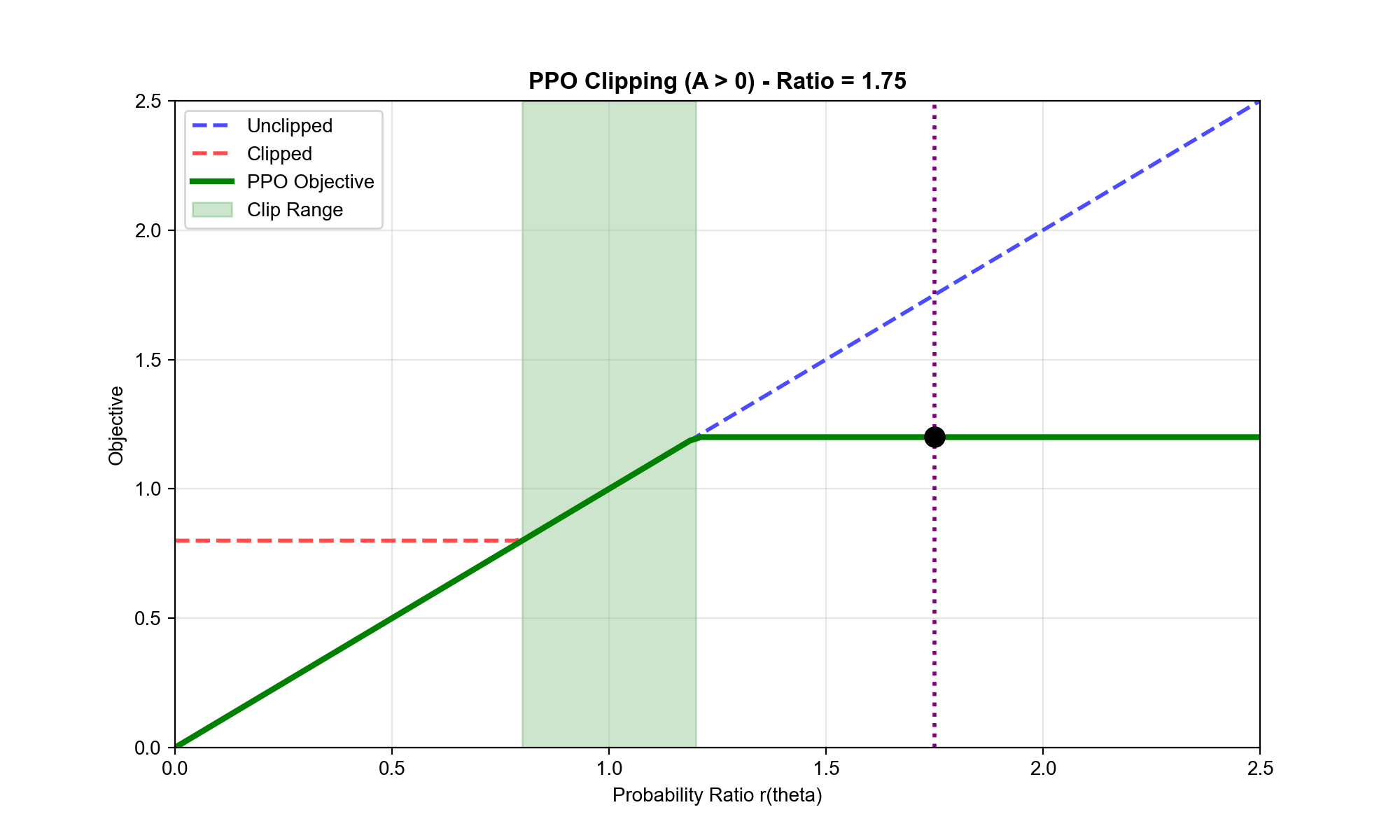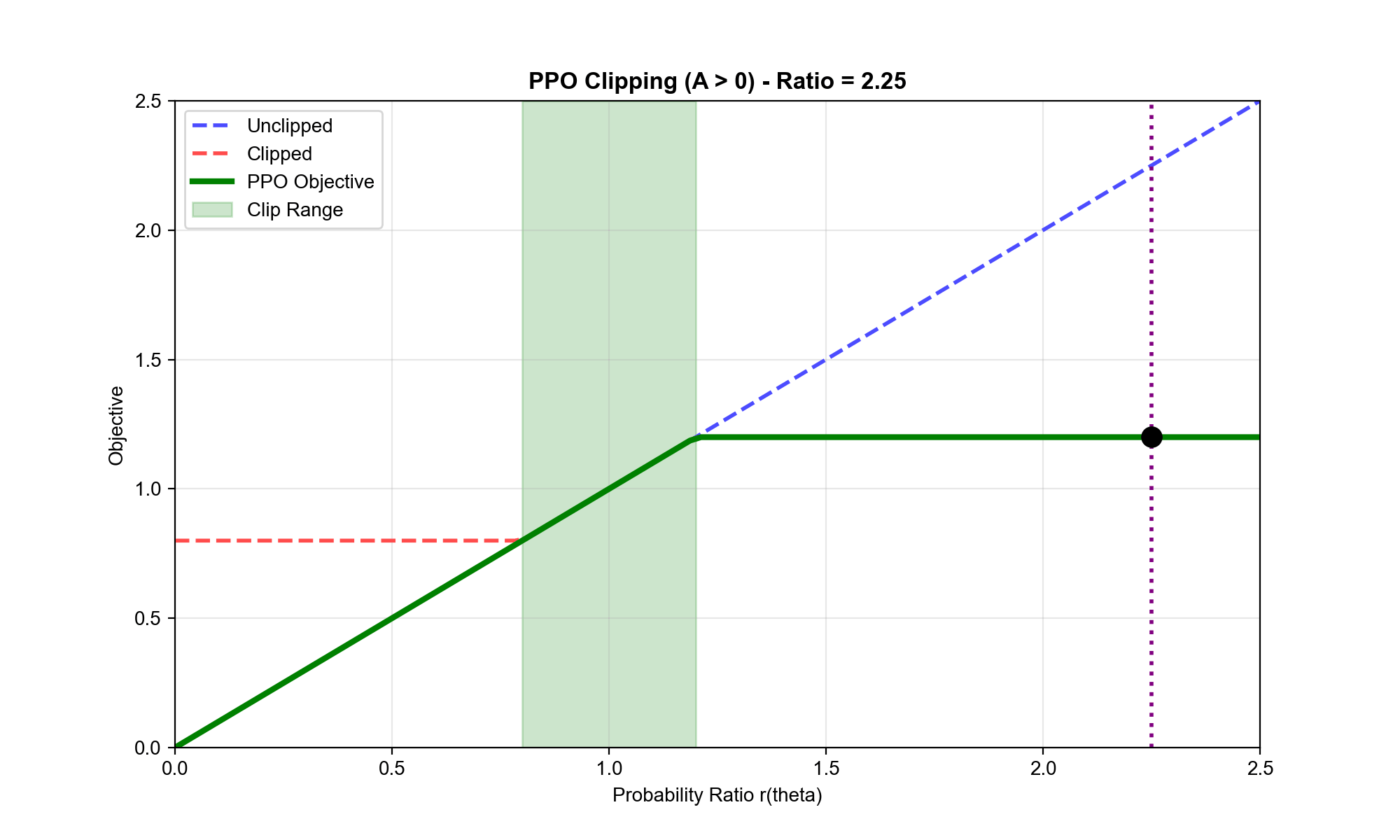
PPO 最流行的变体是裁剪版本，它通过裁剪概率比来限制策略更新：

$$

L^{CLIP}() = _t$$

其中： - 是概率比 - 是裁剪参数，通常取 0.1 或 0.2 - 将限制在 范围内

详细分析目标函数：

让我们分情况讨论：

情况 1：（好动作，我们希望增加其概率）

  • 如果（新策略降低了概率）：，梯度鼓励增加
  • 如果：，梯度继续鼓励增加
  • 如果：，梯度为 0！

最后一种情况很关键：当概率比已经超过 时，目标函数变成常数，梯度为 0 。这阻止了策略继续朝这个方向更新——即使优势很大，我们也不能过度增加动作概率。

情况 2：（坏动作，我们希望降低其概率）

  • 如果（新策略增加了概率）：（负值），梯度鼓励降低
  • 如果：，梯度继续鼓励降低
  • 如果：，梯度为 0！

同样，当概率比已经低于 时，梯度变为 0，阻止进一步降低动作概率。

直觉总结： PPO-Clip 的目标函数是"悲观"的——它取两个目标中较小的那个。这确保了： - 不会因为一个高优势样本就大幅改变策略 - 即使采样噪声导致某些优势估计不准确，策略也不会剧烈波动

PPO-Penalty：惩罚版本

另一种 PPO 变体是将 KL 散度作为惩罚项加入目标函数：

$$

L^{KLPEN}() = _t- _t$$

其中 是 KL 惩罚系数。这等价于 TRPO 的拉格朗日形式，但把约束变成了惩罚项。

自适应 KL 惩罚：

的选择很重要。如果 太小， KL 散度可能过大；如果太大，学习会太保守。 PPO 使用自适应调整：

1
2
3
4
5
6
7
8
9
10
11
def adaptive_kl_penalty(kl, d_target=0.01, beta=1.0):
    """
    自适应调整 KL 惩罚系数
    """
    if kl < d_target / 1.5:
        # KL 太小，可以更激进
        beta /= 2
    elif kl > d_target * 1.5:
        # KL 太大，需要更保守
        beta *= 2
    return beta

实践中， PPO-Clip 比 PPO-Penalty 更常用，因为它不需要调整。

PPO 的完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
from torch.distributions import Categorical, Normal

class PPOAgent:
    def __init__(self, state_dim, action_dim, hidden_dim=64, 
                 lr=3e-4, gamma=0.99, lam=0.95, eps_clip=0.2,
                 c1=0.5, c2=0.01, k_epochs=10, continuous=False):
        """
        PPO 智能体
        
        Args:
            state_dim: 状态维度
            action_dim: 动作维度
            hidden_dim: 隐藏层维度
            lr: 学习率
            gamma: 折扣因子
            lam: GAE 的 lambda 参数
            eps_clip: PPO 裁剪参数
            c1: 价值损失系数
            c2: 熵系数（鼓励探索）
            k_epochs: 每批数据的更新轮数
            continuous: 是否是连续动作空间
        """
        self.continuous = continuous
        self.gamma = gamma
        self.lam = lam
        self.eps_clip = eps_clip
        self.c1 = c1
        self.c2 = c2
        self.k_epochs = k_epochs
        
        if continuous:
            # 连续动作空间：输出均值和标准差
            self.policy_mean = nn.Sequential(
                nn.Linear(state_dim, hidden_dim),
                nn.Tanh(),
                nn.Linear(hidden_dim, hidden_dim),
                nn.Tanh(),
                nn.Linear(hidden_dim, action_dim)
            )
            self.policy_log_std = nn.Parameter(torch.zeros(action_dim))
            policy_params = list(self.policy_mean.parameters()) + [self.policy_log_std]
        else:
            # 离散动作空间：输出动作概率
            self.policy = nn.Sequential(
                nn.Linear(state_dim, hidden_dim),
                nn.Tanh(),
                nn.Linear(hidden_dim, hidden_dim),
                nn.Tanh(),
                nn.Linear(hidden_dim, action_dim),
                nn.Softmax(dim=-1)
            )
            policy_params = self.policy.parameters()
        
        # 价值网络
        self.value = nn.Sequential(
            nn.Linear(state_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.Tanh(),
            nn.Linear(hidden_dim, 1)
        )
        
        # 统一优化器
        self.optimizer = optim.Adam(
            list(policy_params) + list(self.value.parameters()), 
            lr=lr
        )
        
    def get_action(self, state):
        """
        根据当前策略采样动作
        
        Returns:
            action: 采样的动作
            log_prob: 动作的对数概率
        """
        state = torch.FloatTensor(state)
        
        if self.continuous:
            mean = self.policy_mean(state)
            std = torch.exp(self.policy_log_std)
            dist = Normal(mean, std)
            action = dist.sample()
            log_prob = dist.log_prob(action).sum()
            return action.detach().numpy(), log_prob.detach()
        else:
            probs = self.policy(state)
            dist = Categorical(probs)
            action = dist.sample()
            return action.item(), dist.log_prob(action).detach()
    
    def evaluate(self, states, actions):
        """
        评估给定状态-动作对的对数概率、价值和熵
        """
        if self.continuous:
            mean = self.policy_mean(states)
            std = torch.exp(self.policy_log_std)
            dist = Normal(mean, std)
            log_probs = dist.log_prob(actions).sum(dim=1)
            entropy = dist.entropy().sum(dim=1).mean()
        else:
            probs = self.policy(states)
            dist = Categorical(probs)
            log_probs = dist.log_prob(actions)
            entropy = dist.entropy().mean()
        
        values = self.value(states).squeeze()
        return log_probs, values, entropy
    
    def compute_gae(self, rewards, values, dones, next_value):
        """
        计算广义优势估计(Generalized Advantage Estimation)
        
        GAE 平衡了偏差和方差：
        - lambda=0: 使用单步 TD 误差，低方差但高偏差
        - lambda=1: 使用蒙特卡洛回报，低偏差但高方差
        - lambda=0.95: 实践中常用的平衡点
        """
        advantages = []
        gae = 0
        values = list(values) + [next_value]
        
        for t in reversed(range(len(rewards))):
            # TD 误差
            delta = rewards[t] + self.gamma * values[t+1] * (1 - dones[t]) - values[t]
            # GAE 递推
            gae = delta + self.gamma * self.lam * (1 - dones[t]) * gae
            advantages.insert(0, gae)
        
        return torch.FloatTensor(advantages)
    
    def update(self, states, actions, old_log_probs, rewards, dones, next_state):
        """
        PPO 更新
        
        核心思想：
        1. 计算优势函数（用 GAE）
        2. 多轮迭代优化，每轮使用 PPO-Clip 目标
        3. 同时优化策略和价值函数
        """
        # 转换为张量
        states = torch.FloatTensor(np.array(states))
        if self.continuous:
            actions = torch.FloatTensor(np.array(actions))
        else:
            actions = torch.LongTensor(actions)
        old_log_probs = torch.stack(old_log_probs)
        
        # 计算优势和回报（不需要梯度）
        with torch.no_grad():
            values = self.value(states).squeeze().numpy()
            next_value = self.value(torch.FloatTensor(next_state)).item()
            advantages = self.compute_gae(rewards, values, dones, next_value)
            returns = advantages + torch.FloatTensor(values)
            
            # 标准化优势（重要！减少方差）
            advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)
        
        # 记录损失用于监控
        policy_losses = []
        value_losses = []
        entropies = []
        
        # 多轮优化
        for _ in range(self.k_epochs):
            # 评估当前策略
            log_probs, value_pred, entropy = self.evaluate(states, actions)
            
            # 计算概率比
            ratios = torch.exp(log_probs - old_log_probs)
            
            # PPO-Clip 目标
            surr1 = ratios * advantages
            surr2 = torch.clamp(ratios, 1 - self.eps_clip, 1 + self.eps_clip) * advantages
            policy_loss = -torch.min(surr1, surr2).mean()
            
            # 价值损失（也可以用 clip 版本）
            value_loss = ((value_pred - returns) ** 2).mean()
            
            # 总损失 = 策略损失 + 价值损失系数 * 价值损失 - 熵系数 * 熵
            # 注意：熵是负的（我们最大化熵，所以减去）
            loss = policy_loss + self.c1 * value_loss - self.c2 * entropy
            
            # 梯度更新
            self.optimizer.zero_grad()
            loss.backward()
            # 梯度裁剪（可选，但推荐）
            if self.continuous:
                nn.utils.clip_grad_norm_(
                    list(self.policy_mean.parameters()) + [self.policy_log_std] + 
                    list(self.value.parameters()), 
                    0.5
                )
            else:
                nn.utils.clip_grad_norm_(
                    list(self.policy.parameters()) + list(self.value.parameters()), 
                    0.5
                )
            self.optimizer.step()
            
            policy_losses.append(policy_loss.item())
            value_losses.append(value_loss.item())
            entropies.append(entropy.item())
        
        return {
            'policy_loss': np.mean(policy_losses),
            'value_loss': np.mean(value_losses),
            'entropy': np.mean(entropies)
        }

def train_ppo(env_name='CartPole-v1', num_episodes=500, 
              update_freq=2048, batch_size=64, render=False):
    """
    PPO 训练流程
    
    Args:
        env_name: 环境名称
        num_episodes: 训练的 episode 数
        update_freq: 每多少步更新一次
        batch_size: 小批量大小（用于并行计算，这里简化为全批量）
        render: 是否渲染环境
    """
    import gym
    env = gym.make(env_name)
    state_dim = env.observation_space.shape[0]
    
    # 检查动作空间类型
    if isinstance(env.action_space, gym.spaces.Discrete):
        action_dim = env.action_space.n
        continuous = False
    else:
        action_dim = env.action_space.shape[0]
        continuous = True
    
    agent = PPOAgent(state_dim, action_dim, continuous=continuous)
    
    # 数据缓冲区
    states, actions, log_probs, rewards, dones = [], [], [], [], []
    
    episode_rewards = []
    total_steps = 0
    
    for episode in range(num_episodes):
        state = env.reset()
        episode_reward = 0
        done = False
        
        while not done:
            if render:
                env.render()
            
            # 采样动作
            action, log_prob = agent.get_action(state)
            next_state, reward, done, _ = env.step(action)
            
            # 存储经验
            states.append(state)
            actions.append(action)
            log_probs.append(log_prob)
            rewards.append(reward)
            dones.append(done)
            
            state = next_state
            episode_reward += reward
            total_steps += 1
            
            # 达到更新频率时进行更新
            if total_steps % update_freq == 0 and len(states) > 0:
                info = agent.update(states, actions, log_probs, rewards, dones, state)
                # 清空缓冲区
                states, actions, log_probs, rewards, dones = [], [], [], [], []
                print(f"  Update: policy_loss={info['policy_loss']:.4f}, "
                      f"value_loss={info['value_loss']:.4f}, entropy={info['entropy']:.4f}")
        
        episode_rewards.append(episode_reward)
        
        # 每 10 个 episode 打印一次
        if episode % 10 == 0:
            avg_reward = np.mean(episode_rewards[-10:]) if len(episode_rewards) >= 10 else np.mean(episode_rewards)
            print(f"Episode {episode}, Avg Reward (last 10): {avg_reward:.2f}")
    
    env.close()
    return agent, episode_rewards

PPO 的关键技巧

广义优势估计（ GAE）

GAE 是一个计算优势函数的技巧，通过参数 在偏差和方差之间取得平衡：

$$

A^{GAE(, )}t = {l=0}^{} ()^l _{t+l}$$

其中 是 TD 误差。

特殊情况： - ：（单步 TD，低方差高偏差） - ：（蒙特卡洛，高方差低偏差）

实践中通常取，这是一个很好的平衡点。

价值函数裁剪

为了进一步稳定训练，可以对价值函数也应用裁剪：

$$

L^{VF}() = $$

这防止价值函数的更新过于激进。

学习率退火

在训练后期降低学习率可以提升最终性能：

1
2
3
4
5
6
7
8
9
10
def linear_schedule(initial_lr, final_lr, current_step, total_steps):
    """线性退火"""
    progress = current_step / total_steps
    return initial_lr + (final_lr - initial_lr) * progress

# 更常用的是 cosine 退火
def cosine_schedule(initial_lr, final_lr, current_step, total_steps):
    """余弦退火"""
    progress = current_step / total_steps
    return final_lr + 0.5 * (initial_lr - final_lr) * (1 + np.cos(np.pi * progress))

并行环境采样

使用多个并行环境可以大幅提升采样效率和数据多样性：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import multiprocessing as mp

class ParallelEnvs:
    """并行环境封装"""
    def __init__(self, env_name, n_envs=8):
        self.envs = [gym.make(env_name) for _ in range(n_envs)]
        self.n_envs = n_envs
    
    def reset(self):
        return np.array([env.reset() for env in self.envs])
    
    def step(self, actions):
        results = [env.step(a) for env, a in zip(self.envs, actions)]
        states, rewards, dones, infos = zip(*results)
        
        # 自动重置完成的环境
        for i, done in enumerate(dones):
            if done:
                states = list(states)
                states[i] = self.envs[i].reset()
                states = tuple(states)
        
        return np.array(states), np.array(rewards), np.array(dones), infos

正交初始化

对神经网络使用正交初始化可以改善训练稳定性：

1
2
3
4
5
def orthogonal_init(layer, gain=1.0):
    """正交初始化"""
    if isinstance(layer, nn.Linear):
        nn.init.orthogonal_(layer.weight, gain=gain)
        nn.init.constant_(layer.bias, 0)

TRPO 与 PPO 的深度对比

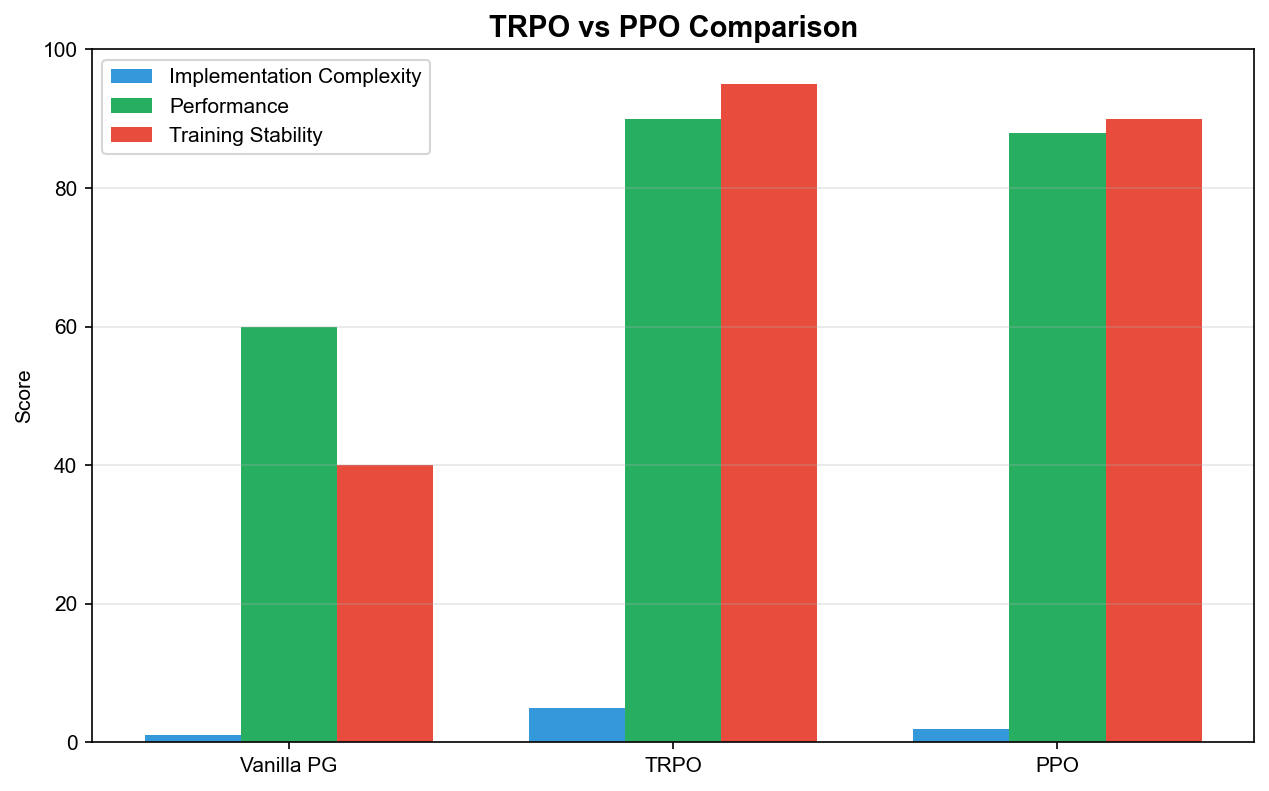
理论保证

方面 TRPO PPO-Clip
策略改进保证 有严格的理论下界 无严格理论保证
KL 约束 硬约束（通过线搜索确保） 软约束（裁剪是启发式的）
更新稳定性 理论保证不会性能下降 经验上稳定，但可能有例外
收敛性 有收敛分析 无严格收敛证明

实现复杂度

方面 TRPO PPO-Clip
优化方法 二阶（自然梯度） 一阶（ SGD/Adam）
是否需要 Fisher 矩阵 是 否
是否需要共轭梯度 是 否
是否需要线搜索 是 否
代码行数（核心） ~300 行 ~100 行
调参复杂度 中等（ 的选择） 低（ 不太敏感）

计算效率

方面 TRPO PPO-Clip
每次更新的反向传播次数 ~20 次（共轭梯度+线搜索） 1 次
内存占用 较高（需要存储 Hessian-向量乘积的中间结果） 较低
并行化难度 较高 较低
GPU 利用率 中等 高

实践性能

在大多数标准强化学习基准上， PPO 与 TRPO 性能相当，有时 PPO 甚至更好。这可能是因为：

  1. 多轮更新： PPO 可以在同一批数据上进行多轮更新（通常 10 轮），而 TRPO 通常只更新一次。这让 PPO 能更充分地利用数据。

  2. 更好的探索： PPO 的熵正则化鼓励探索，而 TRPO 没有显式的探索机制。

  3. 更稳定的价值函数： PPO 通常同时训练策略和价值网络，共享底层表示，这有助于学习更好的特征。

  4. 实现细节： PPO 的简单性使得实现更容易正确，减少了 bug 的可能性。

PPO 在 RLHF 中的应用

PPO 是当今大语言模型对齐（ RLHF）的核心算法。让我们详细了解它在这个场景下的应用。

RLHF 的流程

RLHF（ Reinforcement Learning from Human Feedback）的目标是让语言模型生成更符合人类偏好的回复。流程如下：

  1. 监督微调（ SFT）：在高质量对话数据上微调预训练模型
  2. 训练奖励模型（ RM）：收集人类偏好数据，训练一个模型预测人类会更喜欢哪个回复
  3. PPO 微调：用奖励模型的输出作为奖励信号，用 PPO 微调语言模型

RLHF 中的 PPO 目标

在 RLHF 中， PPO 的目标函数有一些特殊之处：

$$

L^{RLHF}() = {x D, y (y|x)}$$

其中： - 是用户的输入（ prompt） - 是模型生成的回复 - 是奖励模型对回复的评分 - 是参考模型（通常是 SFT 后的模型） - 是 KL 惩罚系数

为什么需要 KL 惩罚？

没有 KL 惩罚，模型可能会找到"黑魔法"来欺骗奖励模型——生成一些奖励模型给高分但实际上质量很差的回复。 KL 惩罚确保模型不会偏离 SFT 模型太远，保持生成的合理性。

实现细节

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
class RLHFPPOTrainer:
    def __init__(self, policy_model, ref_model, reward_model, 
                 kl_coef=0.1, clip_range=0.2):
        """
        RLHF 中的 PPO 训练器
        
        Args:
            policy_model: 要训练的策略模型（语言模型）
            ref_model: 参考模型（冻结的 SFT 模型）
            reward_model: 奖励模型
            kl_coef: KL 惩罚系数
            clip_range: PPO 裁剪范围
        """
        self.policy = policy_model
        self.ref = ref_model
        self.reward = reward_model
        self.kl_coef = kl_coef
        self.clip_range = clip_range
        
        # 冻结参考模型
        for param in self.ref.parameters():
            param.requires_grad = False
    
    def compute_rewards(self, prompts, responses):
        """
        计算奖励（包括 KL 惩罚）
        
        Returns:
            rewards: 最终奖励 = 奖励模型分数 - KL 惩罚
        """
        # 奖励模型评分
        rm_scores = self.reward(prompts, responses)
        
        # 计算 KL 散度
        with torch.no_grad():
            ref_logprobs = self.ref.get_log_probs(prompts, responses)
        policy_logprobs = self.policy.get_log_probs(prompts, responses)
        
        kl = policy_logprobs - ref_logprobs  # 逐 token 的 KL
        kl_penalty = self.kl_coef * kl.sum(dim=1)  # 整个序列的 KL
        
        rewards = rm_scores - kl_penalty
        return rewards, rm_scores, kl_penalty
    
    def ppo_step(self, prompts, old_responses, old_logprobs, advantages):
        """
        PPO 更新步骤
        """
        # 获取新策略下的 log 概率
        new_logprobs = self.policy.get_log_probs(prompts, old_responses)
        
        # 计算概率比
        ratio = torch.exp(new_logprobs - old_logprobs)
        
        # PPO-Clip 目标
        surr1 = ratio * advantages
        surr2 = torch.clamp(ratio, 1 - self.clip_range, 1 + self.clip_range) * advantages
        policy_loss = -torch.min(surr1, surr2).mean()
        
        return policy_loss
    
    def train_step(self, prompts):
        """
        完整的训练步骤
        """
        # 1. 生成回复
        with torch.no_grad():
            responses, old_logprobs = self.policy.generate_with_logprobs(prompts)
        
        # 2. 计算奖励
        rewards, rm_scores, kl_penalty = self.compute_rewards(prompts, responses)
        
        # 3. 计算优势（这里简化，实际可能用更复杂的方法）
        advantages = rewards - rewards.mean()
        advantages = advantages / (advantages.std() + 1e-8)
        
        # 4. PPO 更新
        loss = self.ppo_step(prompts, responses, old_logprobs, advantages)
        
        return loss, rm_scores.mean(), kl_penalty.mean()

RLHF 中 PPO 的挑战

  1. 奖励黑客（ Reward Hacking）：模型可能找到欺骗奖励模型的方法
  2. KL 散度爆炸：如果 KL 惩罚太弱，模型可能快速偏离参考模型
  3. 训练不稳定：语言模型的输出空间巨大，优化 landscape 复杂
  4. 计算成本：需要同时运行多个大模型

最新进展： DPO 和替代方法

由于 RLHF + PPO 的复杂性，最近出现了一些更简单的替代方法：

  • DPO（ Direct Preference Optimization）：直接从偏好数据优化，跳过奖励模型和 PPO
  • IPO（ Identity Preference Optimization）： DPO 的改进版本
  • KTO（ Kahneman-Tversky Optimization）：基于前景理论的优化方法

但 PPO 仍然是很多场景下的首选，特别是当我们需要细粒度控制或在线学习时。

实践建议与调参技巧

超参数选择指南

超参数 典型范围 说明
学习率 1e-4 ~ 3e-4 太大不稳定，太小收敛慢
裁剪参数 0.1 ~ 0.3 0.2 是最常用的
GAE 0.9 ~ 0.99 0.95 通常效果好
折扣因子 0.99 ~ 0.999 任务越长，越接近 1
批量大小 2048 ~ 8192 越大越稳定，但更新越慢
每批更新轮数 3 ~ 10 太多可能过拟合当前数据
熵系数 0.0 ~ 0.01 鼓励探索
价值损失系数 0.5 ~ 1.0

常见问题与解决方案

问题 1：性能不提升或震荡

可能原因： - 学习率太大：降低学习率 - 批量太小：增加批量大小 - 优势估计不准：检查 GAE 实现

问题 2：策略坍塌到确定性策略

可能原因： - 熵系数太小：增加熵系数 - 裁剪参数太小：增加 问题 3：价值函数预测很差

可能原因： - 价值网络容量不足：增加隐藏层大小 - 回报尺度太大：对回报进行归一化 - 学习率不匹配：单独调整价值网络学习率

Debug 技巧

  1. 监控 KL 散度：如果 KL 散度太大（>0.1），说明更新太激进
  2. 监控概率比：大部分比值应该在 范围内
  3. 监控熵：熵应该逐渐下降，但不要降到 0
  4. 可视化优势分布：应该大致对称，均值接近 0

总结

信任域方法的核心思想是约束策略更新幅度，确保学习过程稳定：

  1. TRPO通过 KL 散度约束和自然梯度提供了严格的理论保证，但实现复杂，计算昂贵

  2. PPO通过简单的裁剪机制实现了类似效果，成为了事实上的标准算法

  3. 两者的关键差异：

    • TRPO：二阶优化，硬约束，理论保证
    • PPO：一阶优化，软约束，实践有效

  4. PPO 的成功秘诀：

    • 实现简单，易于调试
    • 可以多次重用数据
    • 与其他技术（ GAE 、并行采样）无缝集成
    • 在 RLHF 等新领域大放异彩

从算法发展的角度看， PPO 代表了一种重要的工程哲学：简单有效的近似往往比复杂的精确方法更有价值。在深度学习时代，这种实用主义的思路尤为重要——我们追求的不是数学上的完美，而是实践中的有效。

下一章，我们将探讨另一个重要方向——模仿学习与逆强化学习：当我们有专家示范但没有明确奖励函数时，如何让智能体学习？

参考文献

  1. Schulman, J., Levine, S., Abbeel, P., Jordan, M., & Moritz, P. (2015). Trust Region Policy Optimization. ICML.
  2. Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv.
  3. Kakade, S., & Langford, J. (2002). Approximately Optimal Approximate Reinforcement Learning. ICML.
  4. Ouyang, L., et al. (2022). Training language models to follow instructions with human feedback. NeurIPS.
  5. Achiam, J. (2018). Spinning Up in Deep RL. OpenAI Documentation.
  6. Amari, S. (1998). Natural Gradient Works Efficiently in Learning. Neural Computation.
  7. Rafailov, R., et al. (2023). Direct Preference Optimization: Your Language Model is Secretly a Reward Model. NeurIPS.

Q&A：常见问题解答

Q1: PPO 和 TRPO 哪个更适合初学者？

A: PPO 。它实现简单，调参容易，性能稳定。建议先掌握 PPO，再学习 TRPO 的理论。

Q2: 裁剪参数 怎么选？

A: 0.2 是最常用的值，适用于大多数任务。如果发现训练不稳定，可以降到 0.1；如果学习太慢，可以尝试 0.3 。

Q3: 为什么 PPO 要多轮更新？

A: 因为 PPO 的裁剪机制限制了每轮更新的幅度。多轮更新可以在裁剪约束内更充分地利用数据。但要注意不能太多轮，否则可能过拟合当前批数据。

Q4: GAE 的 和折扣因子 有什么区别？

A: 控制对未来奖励的重视程度（任务层面）； 控制优势估计中 TD 误差的衰减（估计层面）。两者都在 0 和 1 之间，但作用不同。

Q5: PPO 能用于连续动作空间吗？

A: 可以。用高斯分布参数化动作，学习均值和方差。实现时要注意对数概率的计算。

Q6: 为什么 RLHF 要用 PPO 而不是其他 RL 算法？

A: PPO 稳定性好，不容易导致语言模型"崩溃"（生成胡言乱语）。此外， PPO 的裁剪机制天然与 KL 惩罚配合良好。

Q7: 如何判断 PPO 训练是否正常？

A: 监控以下指标： - 策略损失应该下降 - 平均 KL 散度不应该太大（<0.02 通常是好的） - 裁剪比例不应该太高（<20%） - 平均回报应该上升

Q8: PPO 和 Actor-Critic 有什么关系？

A: PPO 是 Actor-Critic 的一种。 Actor 是策略网络， Critic 是价值网络。 PPO 的特别之处在于它的目标函数设计（裁剪）。

  • 本文标题：强化学习（六）—— PPO 与 TRPO：信任域策略优化
  • 本文作者：Chen Kai
  • 创建时间：2024-09-03 14:30:00
  • 本文链接：https://www.chenk.top/%E5%BC%BA%E5%8C%96%E5%AD%A6%E4%B9%A0%EF%BC%88%E5%85%AD%EF%BC%89%E2%80%94%E2%80%94-PPO%E4%B8%8ETRPO%EF%BC%9A%E4%BF%A1%E4%BB%BB%E5%9F%9F%E7%AD%96%E7%95%A5%E4%BC%98%E5%8C%96/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
 评论