强化学习（五）—— Model-Based 强化学习与世界模型
Chen Kai BOSS
  2024-08-30 09:15:00 2024-08-30 09:15      7.8k 字  33 分钟  

如果说前几章的 Model-Free 方法是"边做边学"——通过大量试错直接优化策略或价值函数,那么 Model-Based 方法则是"先想后做"——通过学习环境的动态模型,在想象中规划未来,大幅提升样本效率。人类和动物的智能很大程度上依赖于对世界的内部模型:国际象棋大师在脑中模拟未来几十步棋局,婴儿通过物理直觉预测物体的运动轨迹。 DeepMind 的 AlphaGo 通过蒙特卡洛树搜索在模拟棋局中规划,OpenAI 的 Dota 2 智能体在训练中使用环境模拟器提前"演练"策略。 Model-Based RL 的核心优势是样本效率——在真实环境中交互很昂贵的场景(如机器人控制、自动驾驶),通过学习的模型生成虚拟经验,可以用 1/10 甚至 1/100 的样本达到 Model-Free 方法的性能。从经典的 Dyna 架构到结合深度学习的 World Models,从隐式规划的 MuZero 到在隐空间梦境中学习的 Dreamer 系列,Model-Based RL 已经在样本效率、泛化能力和可解释性上展现出巨大潜力。本章将系统梳理这一演进路径,深入剖析每个算法的设计动机、数学原理和实现细节。

Model-Based vs Model-Free：两条路径的对比

核心差异

Model-Free RL:直接从经验 学习策略 或价值函数,不显式建模环境动态。

优点: - 算法简单,易于实现 - 不需要对环境做假设 - 在模型复杂或不可知的任务中表现好

缺点: - 样本效率低——需要百万级交互才能学好 - 难以泛化到新任务——策略只对训练环境有效 - 缺乏可解释性——无法理解智能体为什么这样做

Model-Based RL:显式学习环境模型 和奖励函数,利用模型进行规划或生成虚拟数据。

优点: - 样本效率高——可以在想象中学习,减少真实交互 - 泛化能力强——模型学到的动态知识可以迁移到新任务 - 可解释性好——可以可视化智能体对世界的理解

缺点: - 模型误差累积——预测误差会随规划步数指数增长 - 计算昂贵——需要训练额外的模型网络,规划也需要计算 - 难以建模复杂环境——高维观测(如像素)的动态模型很难学

样本效率对比

在经典的控制任务中,Model-Based 方法的样本优势明显:

算法类型 环境 达到专家水平所需样本
DQN (Model-Free) Atari Pong 10M frames
PPO (Model-Free) MuJoCo HalfCheetah 1M steps
Dreamer (Model-Based) DMControl Walker 100K steps
MBPO (Model-Based) MuJoCo HalfCheetah 100K steps

Model-Based 方法通常只需要 Model-Free 方法 1/10 的样本量!

何时使用 Model-Based 方法

适合场景: - 真实交互成本高(机器人、自动驾驶) - 环境动态相对简单可学(物理模拟器、棋类游戏) - 需要快速适应新任务(迁移学习、元学习) - 需要可解释性和安全保证

不适合场景: - 环境高度随机(如股票市场) - 观测高维且动态复杂(如复杂 3D 游戏) - 有大量免费模拟器(如 Atari,本身就是模拟器)

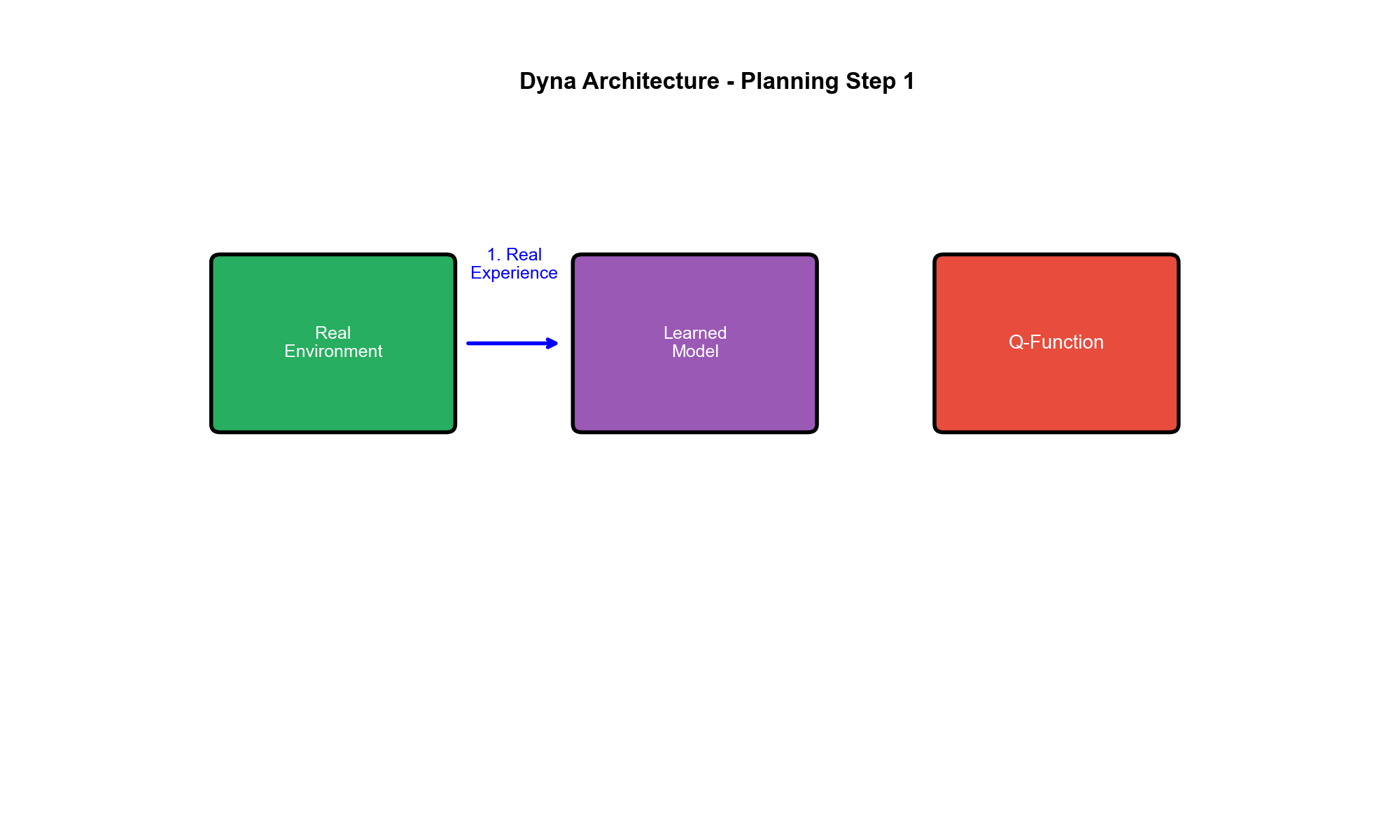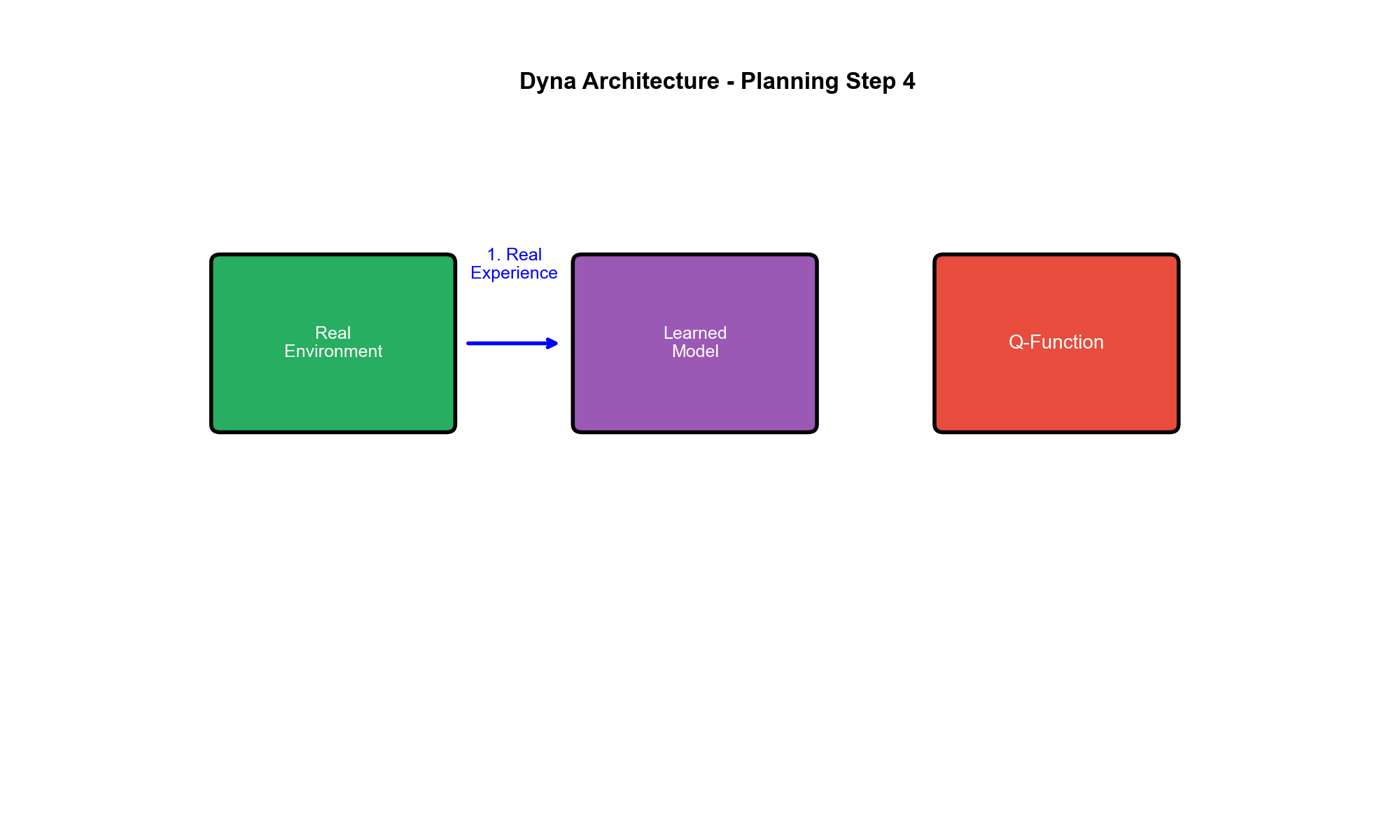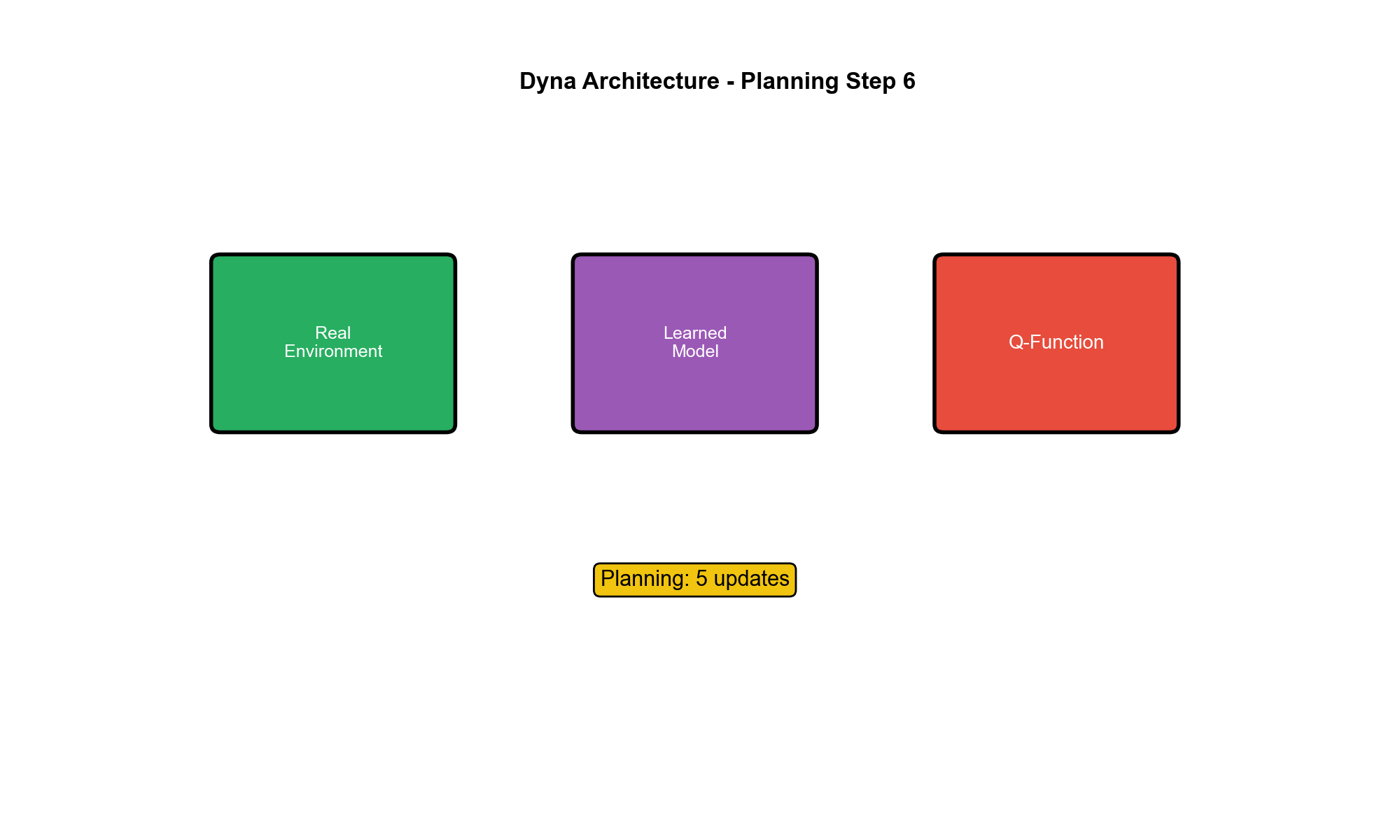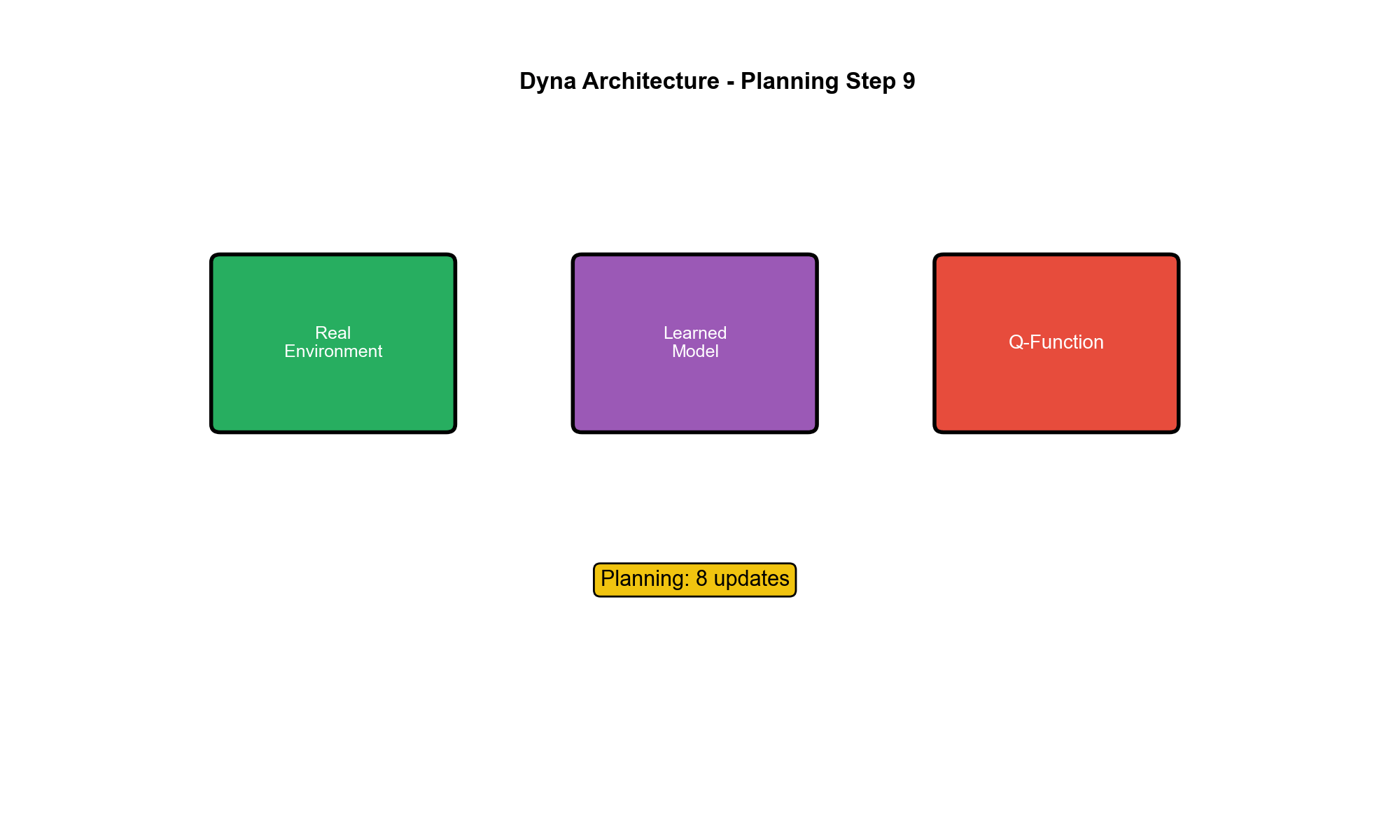
Dyna 架构：整合学习与规划

历史背景

Dyna 架构由 Richard Sutton 在 1990 年提出,是最早系统化的 Model-Based RL 框架。核心思想:交替进行真实经验学习和模拟经验学习。

Dyna 包含三个核心组件:

  1. 直接学习(Direct Learning):从真实环境收集,更新策略/价值函数(Model-Free)
  2. 模型学习(Model Learning):从真实经验学习环境模型3. 规划(Planning):用学习的模型生成模拟经验,进一步更新策略/价值函数

Dyna-Q 算法

Dyna-Q 是 Dyna 架构在 Q-Learning 上的实例化:

算法流程:

  1. 初始化 Q 表 和模型$M(s,a) (r, s')每个时间步真实交互在环境中执行动作a_t (s_t)观测(r_t, s_{t+1})$ - (b) 直接学习:更新 Q 值(标准 Q-Learning): $$

Q(s_t, a_t) Q(s_t, a_t) + $$

  • (c) 模型学习:更新模型:(表格型模型直接记录)
  • (d) 规划:重复 次:
    • 从已访问的状态-动作对中随机采样 - 用模型生成模拟经验: - 用模拟经验更新 Q 值(虚拟 Q-Learning): $$

Q(s, a) Q(s, a) + $$

代码实现(表格型 Dyna-Q)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
import numpy as np
import gym

class DynaQ:
    """Dyna-Q 算法(表格型)"""
    def __init__(self, n_states, n_actions, alpha=0.1, gamma=0.95, epsilon=0.1, planning_steps=5):
        self.n_states = n_states
        self.n_actions = n_actions
        self.alpha = alpha
        self.gamma = gamma
        self.epsilon = epsilon
        self.planning_steps = planning_steps
        
        # Q 表
        self.Q = np.zeros((n_states, n_actions))
        
        # 模型:存储每个(s,a)对应的(r, s')
        self.model = {}
        
        # 已访问的(s,a)对,用于规划时采样
        self.visited = set()
    
    def select_action(self, state):
        """epsilon-greedy 选择动作"""
        if np.random.rand() < self.epsilon:
            return np.random.randint(self.n_actions)
        return np.argmax(self.Q[state])
    
    def update_q(self, s, a, r, s_next):
        """Q-Learning 更新"""
        target = r + self.gamma * np.max(self.Q[s_next])
        self.Q[s, a] += self.alpha * (target - self.Q[s, a])
    
    def learn(self, state, action, reward, next_state):
        """Dyna-Q 学习步骤"""
        # (a) 直接学习
        self.update_q(state, action, reward, next_state)
        
        # (b) 模型学习
        self.model[(state, action)] = (reward, next_state)
        self.visited.add((state, action))
        
        # (c) 规划(用模型生成模拟经验)
        for _ in range(self.planning_steps):
            if not self.visited:
                break
            # 随机采样已访问的(s,a)
            s, a = list(self.visited)[np.random.randint(len(self.visited))]
            r, s_next = self.model[(s, a)]
            # 用模拟经验更新 Q 值
            self.update_q(s, a, r, s_next)

def train_dyna_q(env_name='FrozenLake-v1', episodes=500):
    """训练 Dyna-Q"""
    env = gym.make(env_name, is_slippery=False)
    n_states = env.observation_space.n
    n_actions = env.action_space.n
    
    agent = DynaQ(n_states, n_actions, planning_steps=10)
    
    rewards_history = []
    for episode in range(episodes):
        state = env.reset()
        total_reward = 0
        done = False
        
        while not done:
            action = agent.select_action(state)
            next_state, reward, done, _ = env.step(action)
            agent.learn(state, action, reward, next_state)
            
            state = next_state
            total_reward += reward
        
        rewards_history.append(total_reward)
        
        if (episode + 1) % 50 == 0:
            avg_reward = np.mean(rewards_history[-50:])
            print(f"Episode {episode+1}, Avg Reward: {avg_reward:.2f}")
    
    return agent

# 运行示例
agent = train_dyna_q()

优势与问题

优势: - 简单直观,易于实现 - 样本效率显著提升——每个真实样本可以通过规划产生 个虚拟样本 - 在简单环境(如 GridWorld)中效果卓越

问题 1:模型误差累积

当环境模型 不准确时,用模拟经验更新 Q 值会引入偏差。随着规划步数增加,误差会指数累积,导致策略崩溃。

示例:在 FrozenLake 中,如果模型错误地认为某个状态转移到陷阱的概率是 0,智能体会在规划中高估该状态的价值,导致在真实环境中频繁失败。

问题 2:计算效率

每次真实交互后都要进行 步规划,计算开销是 Model-Free 方法的 倍。在大状态空间中,遍历所有 对不现实。

问题 3:分布偏移(Distribution Shift)

规划时采样的状态可能与策略实际访问的状态分布不同,导致浪费计算在不重要的区域。

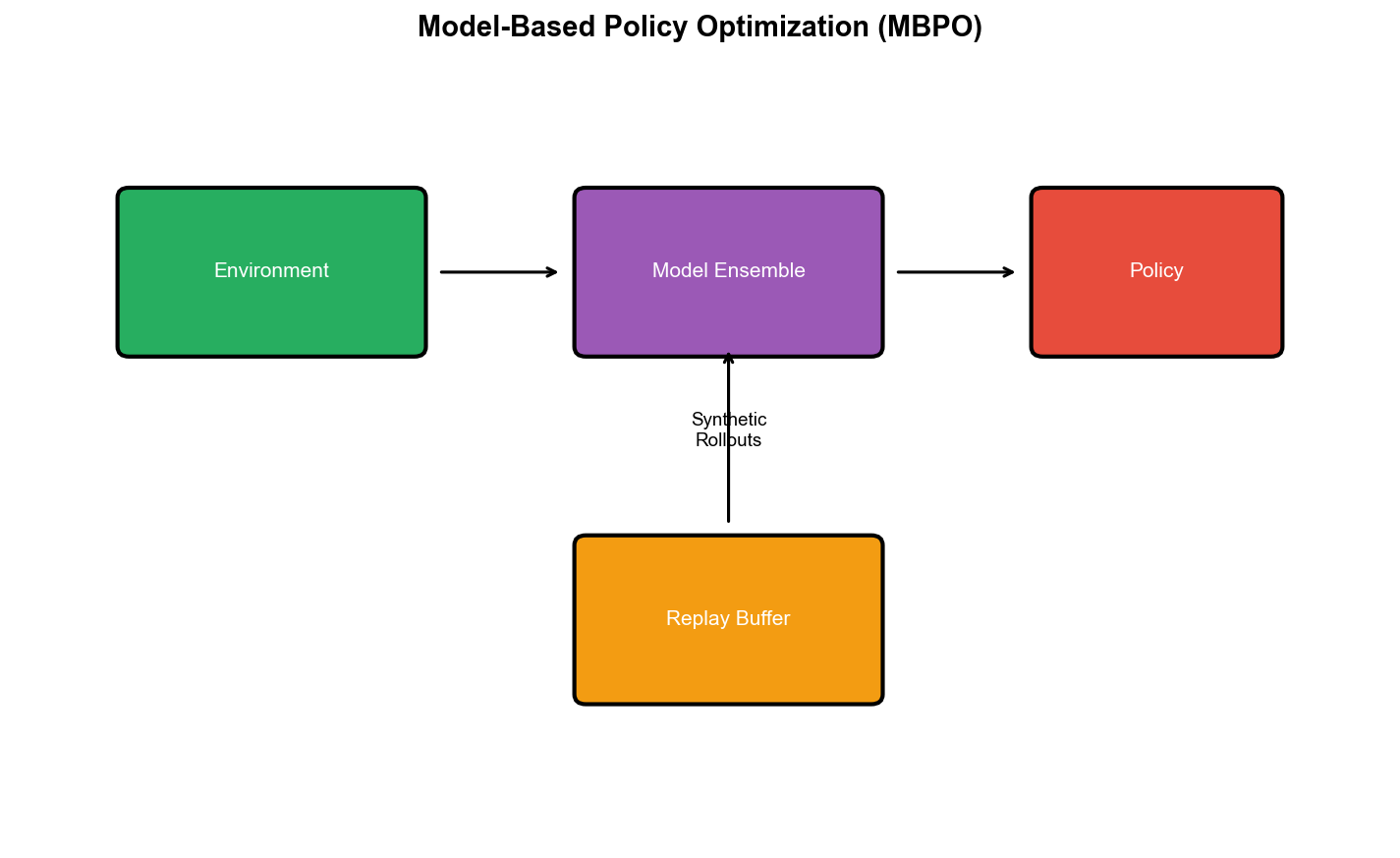
MBPO：通过短视想象缓解模型误差

动机:模型误差的诅咒

在深度 RL 中,环境模型通常是神经网络。问题在于:模型预测误差会随规划长度指数增长。

假设每步预测的均方误差是,那么规划 步后,累积误差约为(线性)到(最坏情况)。当 很大时(如 50 步),即使单步误差很小,累积误差也会让规划完全失效。

Model-Based Policy Optimization (MBPO)(Janner et al., NeurIPS 2019)提出了一个简单而有效的解决方案:只在短视想象中规划。

核心思想

MBPO 的关键洞察: - 长期规划(H=50)容易受模型误差影响 - 短期规划(H=1-5)模型误差可控 - 结合短视模型想象和 Model-Free 优化,可以兼得样本效率和鲁棒性

算法流程：

  1. 收集真实数据：在环境中执行策略，收集经验存入真实 buffer

  2. 训练动态模型：用训练模型和奖励函数

  3. 生成虚拟数据：

    • 从中采样起始状态
    • 在模型中展开步（通常是 1-5）：

    • 将虚拟经验存入虚拟 buffer

  4. 更新策略：用 SAC（或其他 Model-Free 算法）在混合 buffer上训练

关键细节：展开长度是通过理论分析和实验确定的，通常。Janner 等人证明了存在最优的，使得模型偏差和真实数据方差的权衡最优。

数学分析：为什么短视有效

定义策略的真实回报和模型预测回报的差异：

其中是模型的平均误差，是总变差距离。

这个界告诉我们：折扣因子越小（即越短视），模型误差的影响越小。MBPO 通过限制展开长度，等效地使用了更小的，从而减轻了模型误差的负面影响。

完整代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from collections import deque

# ========== 动态模型 ==========
class EnsembleDynamicsModel(nn.Module):
    """集成动态模型(预测下一状态和奖励)"""
    def __init__(self, state_dim, action_dim, hidden_dim=256, n_models=5):
        super().__init__()
        self.n_models = n_models
        self.models = nn.ModuleList([
            nn.Sequential(
                nn.Linear(state_dim + action_dim, hidden_dim),
                nn.ReLU(),
                nn.Linear(hidden_dim, hidden_dim),
                nn.ReLU(),
                nn.Linear(hidden_dim, state_dim + 1)  # 预测 delta_state 和 reward
            ) for _ in range(n_models)
        ])
    
    def forward(self, state, action):
        """
        返回每个模型的预测
        state: (B, state_dim)
        action: (B, action_dim)
        返回: (n_models, B, state_dim+1)
        """
        x = torch.cat([state, action], dim=-1)
        preds = torch.stack([model(x) for model in self.models])
        return preds
    
    def predict(self, state, action):
        """随机选择一个模型预测(用于展开)"""
        with torch.no_grad():
            preds = self.forward(state, action)
            # 随机选择一个模型的预测
            idx = np.random.randint(self.n_models)
            pred = preds[idx]
            
            delta_state = pred[:, :-1]
            reward = pred[:, -1:]
            
            next_state = state + delta_state  # 预测状态变化量
            return next_state, reward
    
    def train_model(self, replay_buffer, batch_size=256, epochs=5):
        """训练动态模型"""
        optimizer = torch.optim.Adam(self.parameters(), lr=1e-3)
        
        for epoch in range(epochs):
            batch = replay_buffer.sample(batch_size)
            states, actions, rewards, next_states, _ = batch
            
            # 计算真实的 delta_state
            delta_states = next_states - states
            targets = torch.cat([delta_states, rewards.unsqueeze(1)], dim=-1)
            
            # 所有模型的预测
            preds = self.forward(states, actions)
            
            # 最大似然损失(每个模型独立)
            losses = []
            for i in range(self.n_models):
                loss = F.mse_loss(preds[i], targets)
                losses.append(loss)
            
            total_loss = sum(losses)
            
            optimizer.zero_grad()
            total_loss.backward()
            optimizer.step()
        
        return total_loss.item()

# ========== MBPO 算法 ==========
class MBPO:
    """Model-Based Policy Optimization"""
    def __init__(self, env, state_dim, action_dim, rollout_length=5):
        self.env = env
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.rollout_length = rollout_length
        
        # 真实环境 buffer
        self.env_buffer = ReplayBuffer(state_dim, action_dim, max_size=1_000_000)
        
        # 虚拟环境 buffer
        self.model_buffer = ReplayBuffer(state_dim, action_dim, max_size=1_000_000)
        
        # 动态模型
        self.dynamics_model = EnsembleDynamicsModel(state_dim, action_dim)
        
        # 策略(这里用 SAC,也可以用其他 Model-Free 算法)
        self.policy = SAC(state_dim, action_dim)
    
    def collect_real_data(self, n_steps=1000):
        """收集真实环境数据"""
        state = self.env.reset()
        for _ in range(n_steps):
            action = self.policy.select_action(state)
            next_state, reward, done, _ = self.env.step(action)
            self.env_buffer.add(state, action, reward, next_state, done)
            
            state = next_state if not done else self.env.reset()
    
    def generate_virtual_data(self, n_rollouts=1000):
        """用模型生成虚拟数据"""
        self.model_buffer.clear()
        
        for _ in range(n_rollouts):
            # 从真实 buffer 采样起始状态
            states, _, _, _, _ = self.env_buffer.sample(1)
            state = states[0]
            
            # 在模型中展开 k 步
            for _ in range(self.rollout_length):
                action = self.policy.select_action(state.cpu().numpy())
                action_tensor = torch.FloatTensor(action).unsqueeze(0)
                
                # 用模型预测
                next_state, reward = self.dynamics_model.predict(state.unsqueeze(0), action_tensor)
                
                # 存入虚拟 buffer
                self.model_buffer.add(
                    state.cpu().numpy(),
                    action,
                    reward.item(),
                    next_state.squeeze(0).cpu().numpy(),
                    False  # 虚拟数据不设置 done
                )
                
                state = next_state.squeeze(0)
    
    def train(self, total_steps=100_000):
        """MBPO 训练循环"""
        # 初始随机数据收集
        self.collect_real_data(n_steps=5000)
        
        for step in range(total_steps):
            # 1. 收集少量真实数据
            self.collect_real_data(n_steps=100)
            
            # 2. 训练动态模型
            if step % 250 == 0:
                model_loss = self.dynamics_model.train_model(self.env_buffer)
                print(f"Step {step}, Model Loss: {model_loss:.4f}")
            
            # 3. 生成虚拟数据
            self.generate_virtual_data(n_rollouts=1000)
            
            # 4. 混合训练策略(真实+虚拟)
            for _ in range(20):
                # 从两个 buffer 采样(可以调整比例)
                real_batch = self.env_buffer.sample(128)
                model_batch = self.model_buffer.sample(128)
                
                # 混合 batch(这里简化为分别训练)
                self.policy.train_step(real_batch)
                self.policy.train_step(model_batch)
            
            # 5. 评估
            if step % 1000 == 0:
                eval_reward = self.evaluate()
                print(f"Step {step}, Eval Reward: {eval_reward:.2f}")
    
    def evaluate(self, n_episodes=10):
        """评估策略"""
        total_rewards = []
        for _ in range(n_episodes):
            state = self.env.reset()
            episode_reward = 0
            done = False
            while not done:
                action = self.policy.select_action(state, deterministic=True)
                state, reward, done, _ = self.env.step(action)
                episode_reward += reward
            total_rewards.append(episode_reward)
        return np.mean(total_rewards)

实验效果

Janner et al.的论文显示,MBPO 在 MuJoCo 连续控制任务上取得了突破:

  • HalfCheetah:100K 步达到 10000 分(SAC 需要 1M 步)
  • Hopper:100K 步达到 3000 分,样本效率是 SAC 的 10 倍
  • Humanoid:首次在 100K 步内学会站立行走

关键发现:

  1. 展开长度 在大多数任务上最优(短视最好!)
  2. 集成模型(5 个网络取平均)显著提升鲁棒性
  3. 虚拟数据和真实数据的混合比例是 4:1 最佳

论文链接:arXiv:1906.08253

World Models：在压缩的潜在空间中梦境

动机:像素空间的模型学习困境

MBPO 在低维状态空间(如 MuJoCo 的关节角度)表现优异,但在高维观测(如 Atari 的 像素)中直接建模 几乎不可能——像素级预测需要学习每个像素的 RGB 值,计算和存储开销巨大,且模型容易过拟合。

World Models(Ha & Schmidhuber, NeurIPS 2018)提出了一个优雅的解决方案:不在原始像素空间建模,而在压缩的潜在空间中学习动态。

核心架构

World Models 包含三个核心组件:

1. Vision 模块(V):变分自编码器(VAE)

将高维观测(像素)压缩到低维潜在编码:

$$

z_t q_(z|o_t) = ((o_t), (o_t)) $$

VAE 的目标是最大化 ELBO:

2. Memory 模块(M):循环神经网络(RNN/LSTM)

在潜在空间预测下一个状态:

其中 是 RNN 的隐状态, 用混合密度网络(MDN-RNN)参数化,输出 的高斯混合分布。

3. Controller 模块(C):策略网络

从潜在状态选择动作:

$$

a_t = C(z_t, h_t) $$

Controller 是一个简单的线性策略或小型 MLP 。

训练流程

阶段 1:数据收集

用随机策略在环境中收集轨迹。

阶段 2:训练 V 模块

用所有观测训练 VAE,学习压缩表示。

阶段 3:训练 M 模块

用编码后的轨迹 训练 MDN-RNN,学习潜在动态:

阶段 4:训练 C 模块

在"梦境"中训练策略——完全在学习的模型 中展开,不再与真实环境交互:

其中轨迹 由模型 生成。 Controller 用进化策略(CMA-ES)或强化学习算法优化。

代码实现(简化版)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
import torch
import torch.nn as nn
import torch.nn.functional as F

# ========== VAE 编码器 ==========
class VAE(nn.Module):
    """变分自编码器"""
    def __init__(self, obs_channels=3, latent_dim=32):
        super().__init__()
        # 编码器
        self.encoder = nn.Sequential(
            nn.Conv2d(obs_channels, 32, 4, stride=2, padding=1),
            nn.ReLU(),
            nn.Conv2d(32, 64, 4, stride=2, padding=1),
            nn.ReLU(),
            nn.Conv2d(64, 128, 4, stride=2, padding=1),
            nn.ReLU(),
            nn.Conv2d(128, 256, 4, stride=2, padding=1),
            nn.ReLU(),
            nn.Flatten()
        )
        
        # 潜在分布参数
        self.fc_mu = nn.Linear(256 * 4 * 4, latent_dim)
        self.fc_logvar = nn.Linear(256 * 4 * 4, latent_dim)
        
        # 解码器
        self.fc_decode = nn.Linear(latent_dim, 256 * 4 * 4)
        self.decoder = nn.Sequential(
            nn.ConvTranspose2d(256, 128, 4, stride=2, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(128, 64, 4, stride=2, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(64, 32, 4, stride=2, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(32, obs_channels, 4, stride=2, padding=1),
            nn.Sigmoid()
        )
    
    def encode(self, x):
        """编码到潜在分布"""
        h = self.encoder(x)
        mu = self.fc_mu(h)
        logvar = self.fc_logvar(h)
        return mu, logvar
    
    def reparameterize(self, mu, logvar):
        """重参数化技巧"""
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mu + eps * std
    
    def decode(self, z):
        """解码到图像"""
        h = self.fc_decode(z)
        h = h.view(-1, 256, 4, 4)
        return self.decoder(h)
    
    def forward(self, x):
        mu, logvar = self.encode(x)
        z = self.reparameterize(mu, logvar)
        recon = self.decode(z)
        return recon, mu, logvar
    
    def loss_function(self, recon, x, mu, logvar):
        """VAE 损失(重构+KL 散度)"""
        recon_loss = F.mse_loss(recon, x, reduction='sum')
        kl_loss = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
        return recon_loss + kl_loss

# ========== MDN-RNN ==========
class MDNRNN(nn.Module):
    """混合密度网络 RNN"""
    def __init__(self, latent_dim, action_dim, hidden_dim=256, n_gaussians=5):
        super().__init__()
        self.hidden_dim = hidden_dim
        self.n_gaussians = n_gaussians
        
        # LSTM
        self.lstm = nn.LSTM(latent_dim + action_dim, hidden_dim, batch_first=True)
        
        # MDN 参数输出
        self.mdn_mu = nn.Linear(hidden_dim, latent_dim * n_gaussians)
        self.mdn_sigma = nn.Linear(hidden_dim, latent_dim * n_gaussians)
        self.mdn_pi = nn.Linear(hidden_dim, n_gaussians)
    
    def forward(self, z, a, h=None):
        """
        预测下一个潜在状态的分布
        z: (B, T, latent_dim)
        a: (B, T, action_dim)
        h: 隐状态(可选)
        """
        x = torch.cat([z, a], dim=-1)
        lstm_out, h_next = self.lstm(x, h)
        
        # MDN 参数
        mu = self.mdn_mu(lstm_out)
        sigma = torch.exp(self.mdn_sigma(lstm_out))
        pi = F.softmax(self.mdn_pi(lstm_out), dim=-1)
        
        return mu, sigma, pi, h_next
    
    def sample(self, mu, sigma, pi):
        """从混合高斯分布采样"""
        # 选择高斯分量
        k = torch.multinomial(pi, 1).squeeze(-1)
        
        # 从选中的高斯采样
        mu_k = mu.gather(-1, k.unsqueeze(-1).expand(-1, -1, mu.size(-1) // self.n_gaussians))
        sigma_k = sigma.gather(-1, k.unsqueeze(-1).expand(-1, -1, sigma.size(-1) // self.n_gaussians))
        
        z_next = mu_k + sigma_k * torch.randn_like(mu_k)
        return z_next

# ========== Controller ==========
class Controller(nn.Module):
    """简单的线性策略"""
    def __init__(self, latent_dim, hidden_dim, action_dim):
        super().__init__()
        self.fc = nn.Linear(latent_dim + hidden_dim, action_dim)
    
    def forward(self, z, h):
        """输出动作"""
        x = torch.cat([z, h], dim=-1)
        return torch.tanh(self.fc(x))

# ========== 训练流程 ==========
def train_world_models(env, episodes=1000):
    """训练 World Models"""
    # 1. 收集数据
    print("Collecting data...")
    trajectories = collect_random_trajectories(env, episodes)
    
    # 2. 训练 VAE
    print("Training VAE...")
    vae = VAE()
    optimizer_vae = torch.optim.Adam(vae.parameters(), lr=1e-4)
    
    for epoch in range(50):
        total_loss = 0
        for obs_batch in get_obs_batches(trajectories):
            recon, mu, logvar = vae(obs_batch)
            loss = vae.loss_function(recon, obs_batch, mu, logvar)
            
            optimizer_vae.zero_grad()
            loss.backward()
            optimizer_vae.step()
            
            total_loss += loss.item()
        print(f"VAE Epoch {epoch}, Loss: {total_loss:.2f}")
    
    # 3. 编码所有观测到潜在空间
    print("Encoding observations...")
    latent_trajectories = encode_trajectories(vae, trajectories)
    
    # 4. 训练 MDN-RNN
    print("Training MDN-RNN...")
    mdn_rnn = MDNRNN(latent_dim=32, action_dim=env.action_space.shape[0])
    optimizer_rnn = torch.optim.Adam(mdn_rnn.parameters(), lr=1e-3)
    
    for epoch in range(50):
        total_loss = 0
        for z_seq, a_seq in get_latent_batches(latent_trajectories):
            mu, sigma, pi, _ = mdn_rnn(z_seq[:, :-1], a_seq[:, :-1])
            # 负对数似然损失
            loss = mdn_nll_loss(z_seq[:, 1:], mu, sigma, pi)
            
            optimizer_rnn.zero_grad()
            loss.backward()
            optimizer_rnn.step()
            
            total_loss += loss.item()
        print(f"RNN Epoch {epoch}, Loss: {total_loss:.2f}")
    
    # 5. 在梦境中训练 Controller
    print("Training Controller in dream...")
    controller = Controller(latent_dim=32, hidden_dim=256, action_dim=env.action_space.shape[0])
    # 用 CMA-ES 或 PPO 优化 controller(略)
    
    return vae, mdn_rnn, controller

实验效果

Ha & Schmidhuber 在 CarRacing 游戏上展示了 World Models 的强大能力:

  • Controller 只有 867 个参数(vs DQN 的 170 万)
  • 在模型中训练 10000 个虚拟 episode,完全不与真实环境交互
  • 达到 900+分(接近人类水平)
  • 可视化显示模型学会了预测赛道、背景和车辆行为

更令人震撼的是:即使在有视觉故障的环境中,智能体也能依靠内部模型完成任务——展示了世界模型的鲁棒性。

论文链接:arXiv:1803.10122

Dreamer：在潜在空间中端到端学习

从 World Models 到 Dreamer

World Models 的一个局限是分阶段训练:先训练 VAE,再训练 RNN,最后训练 Controller,每个阶段独立优化。这导致: - VAE 可能学到的表示不适合做规划 - RNN 的预测误差无法反向传播到 VAE 改进表示 - 需要手动调节各阶段的超参数

Dream to Control (Dreamer)(Hafner et al., ICLR 2020)提出端到端训练的世界模型:所有组件(表示、动态、策略)联合优化,在潜在空间的"梦境"中直接学习策略。

Dreamer 架构

Dreamer 包含四个核心组件：

1. 表示模型（Representation Model）

从观测和历史推断潜在状态：

其中是确定性的循环状态（RNN 隐状态），是随机潜在变量（类似 VAE）。

2. 过渡模型（Transition Model）

在潜在空间预测未来：

3. 观测模型（Observation Model）

解码潜在状态到观测：

4. 奖励模型（Reward Model）

预测奖励：

训练目标

Dreamer 同时优化三个目标:

1. 表示学习损失

这个损失同时训练: - 观测重构(第一项) - 奖励预测(第二项) - 过渡模型和表示的一致性(KL 项)

2. 行为学习损失(在梦境中优化策略)

在潜在空间展开 步,计算梦境中的回报:

$$

V_(s_) = _{p, } $$

其中 是潜在状态， 由奖励模型预测。策略 最大化价值：

3. 价值学习损失

训练价值函数 拟合梦境回报：

完整算法流程

1
2
3
4
5
6
7
8
9
10
11
12
1. 初始化所有模块参数
2. 收集初始数据到 replay buffer
3. Loop:
   a. 从 buffer 采样序列数据
   b. 通过表示模型编码潜在状态 (h, z)
   c. 更新世界模型(表示学习损失)
   d. 在梦境中展开 H 步:
      - 用过渡模型预测未来潜在状态
      - 用奖励模型预测奖励
      - 计算回报
   e. 更新策略(actor loss)和价值函数(critic loss)
   f. 在真实环境中执行策略,收集新数据

代码框架(简化)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
import torch
import torch.nn as nn

class Dreamer:
    """Dreamer 算法"""
    def __init__(self, obs_shape, action_dim, hidden_dim=200, latent_dim=30):
        # 表示模型
        self.encoder = Encoder(obs_shape, latent_dim)
        self.rnn = nn.GRUCell(latent_dim + action_dim, hidden_dim)
        self.posterior = nn.Linear(hidden_dim, latent_dim * 2)  # 输出 mu, std
        
        # 过渡模型
        self.prior = nn.Linear(hidden_dim, latent_dim * 2)
        
        # 观测和奖励模型
        self.decoder = Decoder(latent_dim + hidden_dim, obs_shape)
        self.reward_model = nn.Linear(latent_dim + hidden_dim, 1)
        
        # 策略和价值
        self.actor = nn.Linear(latent_dim + hidden_dim, action_dim)
        self.critic = nn.Linear(latent_dim + hidden_dim, 1)
    
    def encode_obs(self, obs, h_prev, z_prev, action):
        """表示学习:编码观测到潜在状态"""
        # RNN 更新
        h = self.rnn(torch.cat([z_prev, action], dim=-1), h_prev)
        
        # 后验分布 q(z|h,o)
        obs_feat = self.encoder(obs)
        post_params = self.posterior(torch.cat([h, obs_feat], dim=-1))
        post_mu, post_std = torch.chunk(post_params, 2, dim=-1)
        post_std = F.softplus(post_std)
        z = post_mu + post_std * torch.randn_like(post_mu)
        
        # 先验分布 p(z|h)
        prior_params = self.prior(h)
        prior_mu, prior_std = torch.chunk(prior_params, 2, dim=-1)
        prior_std = F.softplus(prior_std)
        
        return h, z, (post_mu, post_std, prior_mu, prior_std)
    
    def imagine_trajectory(self, h, z, horizon=15):
        """在梦境中展开轨迹"""
        states = []
        actions = []
        rewards = []
        
        for _ in range(horizon):
            # 策略选择动作
            state = torch.cat([h, z], dim=-1)
            action = torch.tanh(self.actor(state))
            
            # 过渡到下一状态
            h = self.rnn(torch.cat([z, action], dim=-1), h)
            prior_params = self.prior(h)
            prior_mu, prior_std = torch.chunk(prior_params, 2, dim=-1)
            prior_std = F.softplus(prior_std)
            z = prior_mu + prior_std * torch.randn_like(prior_mu)
            
            # 预测奖励
            reward = self.reward_model(torch.cat([h, z], dim=-1))
            
            states.append(state)
            actions.append(action)
            rewards.append(reward)
        
        return states, actions, rewards
    
    def update(self, batch):
        """单步更新"""
        obs_seq, action_seq, reward_seq = batch
        T = obs_seq.size(1)
        
        # === 表示学习 ===
        h = torch.zeros(obs_seq.size(0), 200)
        z = torch.zeros(obs_seq.size(0), 30)
        
        recon_loss = 0
        reward_loss = 0
        kl_loss = 0
        
        for t in range(T):
            h, z, (post_mu, post_std, prior_mu, prior_std) = self.encode_obs(
                obs_seq[:, t], h, z, action_seq[:, t]
            )
            
            # 重构观测
            recon = self.decoder(torch.cat([h, z], dim=-1))
            recon_loss += F.mse_loss(recon, obs_seq[:, t])
            
            # 预测奖励
            pred_reward = self.reward_model(torch.cat([h, z], dim=-1))
            reward_loss += F.mse_loss(pred_reward, reward_seq[:, t])
            
            # KL 散度
            kl = self.kl_divergence(post_mu, post_std, prior_mu, prior_std)
            kl_loss += kl.mean()
        
        world_model_loss = recon_loss + reward_loss + 0.1 * kl_loss
        
        # === 行为学习(在梦境中) ===
        with torch.no_grad():
            h_start = h.detach()
            z_start = z.detach()
        
        states, actions, rewards = self.imagine_trajectory(h_start, z_start, horizon=15)
        
        # 计算回报(lambda-return)
        returns = self.compute_lambda_return(states, rewards, gamma=0.99, lam=0.95)
        
        # Actor 损失
        values = torch.stack([self.critic(s) for s in states])
        actor_loss = -(returns.detach() - values.detach()).mean()
        
        # Critic 损失
        critic_loss = F.mse_loss(values.squeeze(), returns.detach())
        
        # 总损失
        total_loss = world_model_loss + actor_loss + critic_loss
        return total_loss
    
    def kl_divergence(self, mu1, std1, mu2, std2):
        """两个高斯分布的 KL 散度"""
        return torch.log(std2 / std1) + (std1**2 + (mu1 - mu2)**2) / (2 * std2**2) - 0.5
    
    def compute_lambda_return(self, states, rewards, gamma=0.99, lam=0.95):
        """计算 lambda-return(TD(lambda))"""
        values = torch.stack([self.critic(s) for s in states]).squeeze()
        rewards = torch.stack(rewards).squeeze()
        
        returns = []
        g = 0
        for t in reversed(range(len(rewards))):
            delta = rewards[t] + gamma * (values[t+1] if t+1 < len(values) else 0) - values[t]
            g = delta + gamma * lam * g
            returns.insert(0, g + values[t])
        
        return torch.stack(returns)

实验效果

Dreamer 在 DMControl 和 Atari 任务上取得了 SOTA 结果:

  • DMControl Walker:100K 步达到 900 分(SAC 需要 1M 步)
  • Atari Breakout:200K 步达到 400 分,样本效率是 Rainbow 的 5 倍
  • 连续 20 个任务平均:超越所有 baseline(包括 D4PG 、 SAC 、 PlaNet)

关键发现:

  1. 端到端训练的表示质量显著优于分阶段训练
  2. 在梦境中展开 15 步最优(平衡模型误差和长期规划)
  3. KL 正则化至关重要——防止过拟合和模式崩溃

论文链接:arXiv:1912.01603

后续版本DreamerV2(2021)和DreamerV3(2023)进一步改进,DreamerV3 在 Minecraft 等开放世界游戏中取得突破,展示了世界模型的巨大潜力。

MuZero：无需显式模型的规划

动机:为什么不需要完美重构

之前的方法(World Models 、 Dreamer)都试图学习能重构观测的模型——即预测。但对于决策,我们真的需要完美重构每个像素吗?

DeepMind 提出:只需要预测与决策相关的信息(如价值、策略、奖励),而不是完整的观测。

MuZero(Schrittwieser et al., Nature 2020)实现了这个想法:学习一个隐式模型,它不预测观测,只预测价值、策略和奖励——这些是 MCTS 规划所需的全部信息。

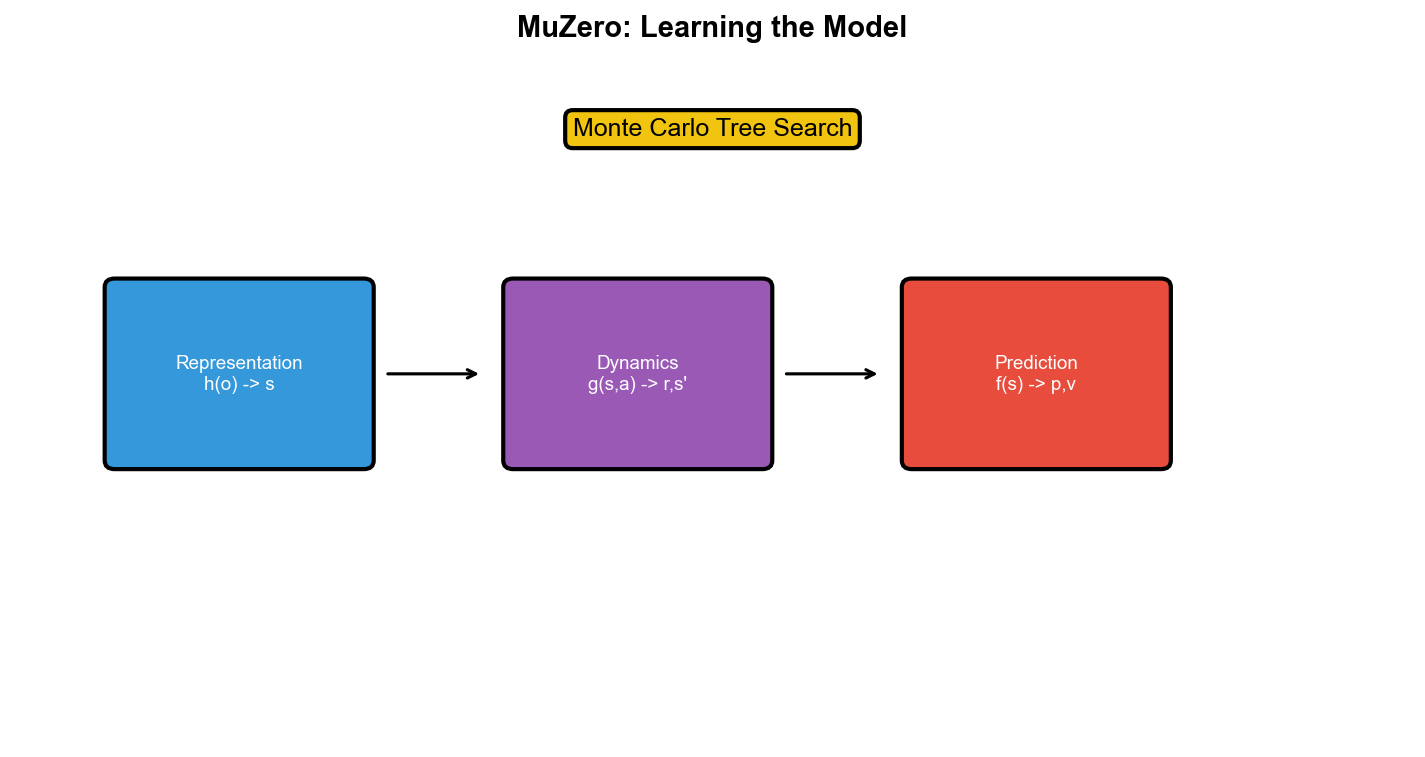
核心架构

MuZero 包含三个网络:

1. 表示网络(Representation Function)

将观测编码到隐藏状态:

$$

s^0 = h(o_1, , o_t) $$

注意: 不是物理状态,而是抽象的"规划状态"。

2. 动态网络(Dynamics Function)

预测下一个隐藏状态和奖励:

$$

s^{k+1}, r^k = g(s^k, a^k) $$

同样, 是抽象的,不对应任何物理意义。

3. 预测网络(Prediction Function)

预测策略和价值:

$$

p^k, v^k = f(s^k) $$

其中 是动作概率, 是状态价值。

训练目标

MuZero 通过 MCTS 在隐藏状态空间中规划,然后用自对弈数据训练。损失函数包含三项:

其中: - 是 MCTS 搜索得到的价值目标 - 是真实奖励 - 是 MCTS 改进后的策略

关键洞察:模型不需要预测观测,只需要预测 MCTS 所需的 三元组。这大大降低了模型学习的难度。

与 AlphaZero 的对比

特性 AlphaZero MuZero
环境模型 需要完美模拟器(如围棋规则) 从数据学习隐式模型
状态表示 显式物理状态 抽象隐藏状态
适用范围 仅限规则已知的游戏 任何环境(包括 Atari)
样本效率 无限模拟 需要真实交互

实验效果

MuZero 在多个领域取得突破:

  • 围棋:与 AlphaZero 相当(ELO ~5000)
  • 国际象棋:略逊于 Stockfish 但远超人类
  • Atari 57 游戏:平均得分超过 R2D2,在一半游戏上达到人类水平
  • DMControl:100K 步超越 Dreamer

最震撼的是:同一个算法,同样的超参数,在完全不同类型的任务(棋类、 Atari 、连续控制)上都取得 SOTA——展示了通用性。

论文链接:arXiv:1911.08265

理论分析与开放问题

Q&A： Model-Based RL 常见问题

Q1: 为什么模型误差会累积?

A: 假设单步预测误差是,那么预测 步后,误差变为 到(取决于误差是否相关)。这是因为每一步的预测都依赖于前一步的状态,错误会层层传播。想象你在地图上每步偏离 1 度,走 10 步后可能完全走错方向。

Q2: 如何评估模型质量?

A: 不能只看重构误差(MSE)!更重要的是:模型预测的轨迹是否导致好的决策。可以用: - 策略评估差异: - 规划质量:在模型中规划的策略在真实环境的表现 - 动态一致性:长期轨迹的分布是否匹配

Q3: Model-Based 能用于部分可观测环境吗?

A: 可以!Dreamer 就是例子——它用 RNN 的隐状态 编码历史,在潜在空间做规划。在 POMDP 中,Model-Based 反而更有优势,因为模型可以学习"记忆"重要的历史信息。

Q4: 如何缓解模型误差?

A: 几种方法:

  1. 短视规划(MBPO):只展开 1-5 步
  2. 集成模型:训练多个模型,取平均或随机采样
  3. 不确定性估计:用贝叶斯神经网络或 Dropout 估计预测不确定性,避免在不确定区域规划
  4. 模型正则化:惩罚过于自信的预测

Q5: Dyna 、 MBPO 、 Dreamer 有什么区别?

A: - Dyna:表格型,模型完美记录转移,适合小环境 - MBPO:学习状态空间的神经网络模型,短视展开,结合 SAC - Dreamer:学习潜在空间的模型,长期展开,端到端训练

共同点:都是"用模型生成数据,用 Model-Free 算法学策略"的框架。

Q6: 为什么 MuZero 不重构观测?

A: 重构高维观测(像素)很难,且很多细节与决策无关(如背景颜色)。 MuZero 只预测决策需要的信息,大大降低学习难度。类比:下围棋时,你不需要预测对手衣服的颜色,只需要预测他会下哪里。

Q7: Model-Based 能迁移到新任务吗?

A: 理论上可以,但实际很难。如果新任务的动态不同(如从走路迁移到跑步),模型需要重新训练或微调。元学习(Meta-Learning)和任务条件模型(Conditional Models)是活跃的研究方向。

Q8: 在哪些任务上 Model-Free 更好?

A: - 环境有便宜的模拟器(如 Atari 、 Go) - 动态极其复杂(如社交互动、股市) - 需要绝对最优性能(Model-Based 的模型误差可能限制上限)

Q9: Dreamer 的"梦境"是什么?

A: 梦境是指在学习的潜在空间模型中展开的想象轨迹。智能体不与真实环境交互,而是:

  1. 从当前潜在状态 出发
  2. 用策略选动作$a_t用模型预测s_{t+1}, r_t$4. 重复 15 步,收集虚拟经验
  3. 用这些经验更新策略

类比人类做白日梦:在脑中模拟未来可能发生的事,从中学习而不需要真正经历。

Q10: 未来 Model-Based RL 的研究方向?

A: - 可组合世界模型:学习可重用的模块(如"物体"、"物理规律"),组合到新场景 - 因果世界模型:不仅预测"会发生什么",还理解"为什么发生" - 终身学习:持续更新模型,适应动态变化的环境 - 安全规划:在模型中验证策略的安全性,再执行

论文推荐

  1. Dyna 架构
    • Integrated Architectures for Learning, Planning, and Reacting Based on Approximating Dynamic Programming (Sutton, 1990)
    • 经典教材:Reinforcement Learning: An Introduction Chapter 8
  2. MBPO
    • When to Trust Your Model: Model-Based Policy Optimization (Janner et al., NeurIPS 2019)
    • 链接:arXiv:1906.08253
  3. World Models
  4. PlaNet
    • Learning Latent Dynamics for Planning from Pixels (Hafner et al., ICML 2019)
    • 链接:arXiv:1811.04551
  5. Dreamer
    • Dream to Control: Learning Behaviors by Latent Imagination (Hafner et al., ICLR 2020)
    • 链接:arXiv:1912.01603
  6. DreamerV2
    • Mastering Atari with Discrete World Models (Hafner et al., ICLR 2021)
    • 链接:arXiv:2010.02193
  7. DreamerV3
    • Mastering Diverse Domains through World Models (Hafner et al., 2023)
    • 链接:arXiv:2301.04104
  8. MuZero
    • Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model (Schrittwieser et al., Nature 2020)
    • 链接:arXiv:1911.08265
  9. STEVE-1(Minecraft with World Models)
    • See, Think, Explore, Search, and Interact: Open-World AGI in Minecraft (2023)
    • 链接:arXiv:2311.08845
  10. Model-Based RL 综述
    • Model-Based Reinforcement Learning: A Survey (Moerland et al., 2023)
    • 链接:arXiv:2006.16712

核心公式总结

Dyna-Q 更新

$$

Q(s,a) Q(s,a) + $$

MBPO 展开

$$

s_{t+1} (|s_t, a_t), r_t = (s_t, a_t), k $$

Dreamer 表示学习

Dreamer 行为学习

MuZero 预测

$$

s^0 = h(o), (s^{k+1}, r^k) = g(s^k, a^k), (p^k, v^k) = f(s^k) $$

总结与展望

Model-Based 强化学习通过学习环境模型,实现了"先想后做"的智能决策,大幅提升了样本效率。从经典的 Dyna 架构到深度学习时代的 MBPO 、 World Models 、 Dreamer 和 MuZero,每一步改进都源于对模型误差、表示学习和规划效率的深刻理解。 Model-Based 方法在样本受限的实际应用(如机器人、自动驾驶)中展现出巨大潜力,但模型误差累积、计算开销和泛化能力仍是挑战。

未来的研究可能融合符号推理、因果建模和神经网络,构建更可解释、可组合、可迁移的世界模型。正如人类通过内部模型理解物理规律、社会规则和他人意图,下一代 AI 系统可能也需要类似的"世界理解"能力——这不仅是强化学习的核心问题,也是通向通用人工智能的关键路径之一。

从 Model-Based 的规划视角出发,下一章我们将进入 AlphaGo 与蒙特卡洛树搜索——通过结合深度学习与经典搜索算法,揭示如何在完美信息博弈中实现超人类水平,并探讨搜索与学习的深层联系。

  • 本文标题：强化学习（五）—— Model-Based 强化学习与世界模型
  • 本文作者：Chen Kai
  • 创建时间：2024-08-30 09:15:00
  • 本文链接：https://www.chenk.top/%E5%BC%BA%E5%8C%96%E5%AD%A6%E4%B9%A0%EF%BC%88%E4%BA%94%EF%BC%89%E2%80%94%E2%80%94-Model-Based%E5%BC%BA%E5%8C%96%E5%AD%A6%E4%B9%A0%E4%B8%8E%E4%B8%96%E7%95%8C%E6%A8%A1%E5%9E%8B/
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
 评论