强化学习（二）—— Q-Learning 与深度 Q 网络（ DQN）

从棋盘游戏到 Atari 电子游戏，价值函数方法一直是强化学习的核心技术路线。 Q-Learning 通过迭代更新状态-动作对的价值，让智能体学会选择最优动作；但面对高维状态空间（比如一个 84x84 像素的游戏画面），传统的表格方法会遭遇维度诅咒。 DeepMind 在 2013 年提出的深度 Q 网络（ DQN）通过引入神经网络作为函数逼近器，结合经验回放和目标网络两大创新，首次让计算机在多款 Atari 游戏中达到超越人类的表现。这一突破不仅推动了深度强化学习的快速发展，也催生了 Double DQN 、 Dueling DQN 、 Prioritized Experience Replay 等一系列改进技术，最终集大成于 Rainbow 算法。本章将从 Q-Learning 的数学原理出发，逐步解构 DQN 的核心机制，并深入分析各种变体的设计动机与实现细节。

Q-Learning 基础：从动态规划到时序差分

Bellman 最优方程与 Q 值

在第一章中我们介绍了价值函数和动作价值函数。对于最优策略，它的 Q 值函数满足 Bellman 最优方程：

Q^{*}(s,a) = [r + _{a'} Q^{*}(s',a')] $$

这个方程的直觉是：在状态下执行动作的最优价值，等于即时奖励加上转移到下一状态后能获得的最大价值（折扣后）。这个递归定义看起来像"鸡生蛋蛋生鸡"，但 Banach 不动点定理保证了它有唯一解，且可以通过迭代逼近。

与策略评估中的不同，对应的是最优策略——一旦我们知道了，就可以通过贪心策略直接得到最优行为。这正是 Q-Learning 的核心思想：不需要显式建模策略，只需学习 Q 函数，策略自然蕴含其中。

Q-Learning 算法：增量式更新

Q-Learning 是一种 off-policy 时序差分（ TD）算法，由 Watkins 在 1989 年提出。它的更新规则是：

Q(s,a) Q(s,a) + $$

这里是学习率，方括号内的部分称为 TD 误差（ temporal difference error）：

TD 误差衡量的是"实际得到的回报"与"当前估计"之间的差距。如果，说明我们低估了这个动作的价值，需要上调；反之则下调。这个更新方式是增量式的——每经历一次转移，就立即更新一次 Q 值，而不需要等到回合结束。

为什么叫 off-policy？因为更新公式中使用的是（对应贪心策略），但实际行为策略可以是任意的——比如 -greedy 策略会以的概率随机探索。这种"说一套做一套"的分离让 Q-Learning 既能保证探索，又能学习最优策略。

收敛性保证： Watkins & Dayan (1992)

Q-Learning 的收敛性由 Watkins 和 Dayan 在 1992 年证明，需要满足以下条件：

表格表示：状态和动作空间都是有限的， Q 值用表格存储
所有状态-动作对被无限次访问：每个都要被更新无穷多次
学习率满足 Robbins-Monro 条件：

直觉上，第一个条件保证意味着学习率的总和足够大，能够克服任意初始误差；第二个条件保证学习率递减到足够小，使得算法最终能稳定在最优值附近。典型的选择是或。

在这些条件下， Q-Learning 以概率 1 收敛到最优 Q 函数，无论使用什么行为策略（只要满足访问条件）。这是一个非常强的理论保证——它告诉我们，即使我们在探索时采用了随机策略，只要足够耐心，最终一定能学到最优策略。

Cliff Walking 示例： Q-Learning 的直觉

让我们用一个经典例子来建立直觉。 Cliff Walking 是一个网格世界：智能体从左下角出发，要到达右下角的目标点，但底部有一排悬崖，掉下去会获得-100 的奖励并回到起点。每走一步获得-1 的奖励。

在这个环境中，最优路径是紧贴悬崖走（最短路径），但探索时很容易掉下去。 Q-Learning 的更新会发生什么？

初始时所有 Q 值为 0 。当智能体第一次掉下悬崖后，转移会导致：

Q(s_{}, ) + = -100 $$

这个负值会传播到前一个状态：当从向右走到时：

Q(s_{}, ) + $$

如果，且已经是-100，那么会选择向右或向上（ Q 值更高），负值不会直接传播。但如果智能体继续探索并多次掉崖，悬崖边缘的 Q 值会逐渐下降，迫使策略学习绕路。

这个例子展示了 Q-Learning 的两个特性： 1. 负奖励的传播：危险区域的低 Q 值会向前传播，形成"禁区" 2. off-policy 的优势：即使行为策略经常掉崖（探索），学习的仍然对应最优路径（利用）

完整的 Python 实现如下：

import numpy as np
import matplotlib.pyplot as plt

class CliffWalkingEnv:
    """
    Cliff Walking 环境： 4x12 的网格世界
    起点：(3,0)，终点：(3,11)
    悬崖：(3,1)到(3,10)
    """
    def __init__(self):
        self.height = 4
        self.width = 12
        self.start = (3, 0)
        self.goal = (3, 11)
        self.cliff = [(3, i) for i in range(1, 11)]
        
    def reset(self):
        self.state = self.start
        return self.state
    
    def step(self, action):
        # 动作： 0=上, 1=右, 2=下, 3=左
        row, col = self.state
        if action == 0:
            row = max(0, row - 1)
        elif action == 1:
            col = min(self.width - 1, col + 1)
        elif action == 2:
            row = min(self.height - 1, row + 1)
        elif action == 3:
            col = max(0, col - 1)
        
        next_state = (row, col)
        
        # 检查是否掉悬崖
        if next_state in self.cliff:
            reward = -100
            done = False
            next_state = self.start  # 回到起点
        elif next_state == self.goal:
            reward = 0  # 到达终点，不给奖励（因为每步-1 已经惩罚了）
            done = True
        else:
            reward = -1
            done = False
        
        self.state = next_state
        return next_state, reward, done

def q_learning(env, episodes=500, alpha=0.1, gamma=0.99, epsilon=0.1):
    """
    Q-Learning 算法
    """
    Q = {}  # 用字典存储 Q 值，稀疏表示
    for s in [(i,j) for i in range(env.height) for j in range(env.width)]:
        for a in range(4):
            Q[(s, a)] = 0.0
    
    rewards_per_episode = []
    
    for ep in range(episodes):
        state = env.reset()
        total_reward = 0
        steps = 0
        
        while steps < 1000:  # 防止无限循环
            # epsilon-greedy 策略
            if np.random.rand() < epsilon:
                action = np.random.randint(4)
            else:
                q_values = [Q[(state, a)] for a in range(4)]
                action = np.argmax(q_values)
            
            next_state, reward, done = env.step(action)
            total_reward += reward
            
            # Q-Learning 更新
            best_next_q = max([Q[(next_state, a)] for a in range(4)])
            td_error = reward + gamma * best_next_q - Q[(state, action)]
            Q[(state, action)] += alpha * td_error
            
            state = next_state
            steps += 1
            
            if done:
                break
        
        rewards_per_episode.append(total_reward)
        
        if (ep + 1) % 100 == 0:
            avg_reward = np.mean(rewards_per_episode[-100:])
            print(f"Episode {ep+1}, Avg Reward: {avg_reward:.2f}")
    
    return Q, rewards_per_episode

# 运行实验
env = CliffWalkingEnv()
Q, rewards = q_learning(env, episodes=500)

# 可视化学习曲线
plt.figure(figsize=(10, 5))
plt.plot(rewards, alpha=0.3)
plt.plot(np.convolve(rewards, np.ones(50)/50, mode='valid'), linewidth=2)
plt.xlabel('Episode')
plt.ylabel('Total Reward')
plt.title('Q-Learning on Cliff Walking')
plt.grid(True)
plt.show()

# 提取最优策略
def extract_policy(Q, env):
    policy = {}
    for s in [(i,j) for i in range(env.height) for j in range(env.width)]:
        q_values = [Q[(s, a)] for a in range(4)]
        policy[s] = np.argmax(q_values)
    return policy

optimal_policy = extract_policy(Q, env)
print("最优策略示例（起点附近）：", 
      {s: ['↑','→','↓','←'][optimal_policy[s]] 
       for s in [(3,0), (2,0), (2,1), (2,2)]})

这段代码展示了 Q-Learning 的完整流程：初始化 Q 表、与环境交互、计算 TD 误差、更新 Q 值。运行后你会发现，学习曲线在初期震荡很大（频繁掉崖），但随着训练进行，智能体逐渐学会绕开悬崖，最终稳定在-13 左右的回报（最优路径长度）。

函数逼近的必要性与挑战

维度诅咒：为什么表格不够用

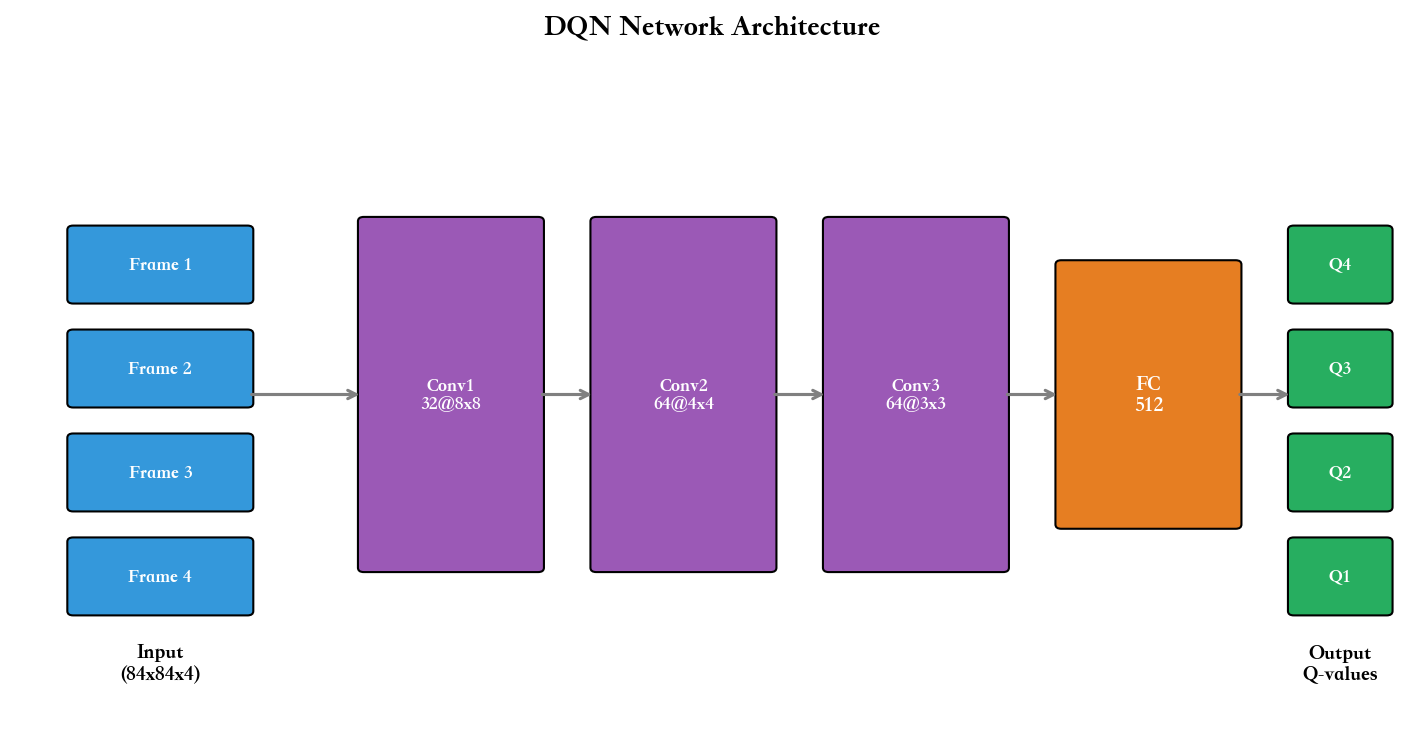
Cliff Walking 只有 48 个状态，用表格存储 Q 值完全没问题。但考虑 Atari 游戏：

Breakout（打砖块）：输入是 84x84x4 的灰度帧栈（ 4 帧历史），状态空间大小约为
Go（围棋）： 19x19 棋盘，每个交叉点有 3 种状态（黑/白/空），状态空间即使用最先进的存储技术，也无法为每个状态存储一个 Q 值。更严重的是，在如此巨大的空间中，智能体几乎不可能两次遇到完全相同的状态——这意味着每个状态只会被访问一次，无法满足 Q-Learning 的收敛条件。

解决方案是函数逼近（ function approximation）：用一个参数化的函数来近似真实的 Q 值，其中是可学习的参数。对于神经网络，是权重和偏置。这样，即使遇到新状态，只要它与见过的状态"相似"，网络也能通过泛化给出合理的 Q 值估计。

Deadly Triad：稳定性的三重威胁

然而，函数逼近带来了严重的稳定性问题。 Sutton 和 Barto 在《 Reinforcement Learning: An Introduction 》中总结了 Deadly Triad（致命三角）：

Bootstrapping（自举）：用估计值更新估计值
- Q-Learning 的更新目标本身依赖于 Q 的估计
Function Approximation（函数逼近）：用参数化函数替代表格
- 更新一个状态的 Q 值会影响到其他"相似"状态的 Q 值
Off-Policy（离策略）：学习的策略与行为策略不同
- 行为策略的分布与目标策略不同，引入分布偏移

这三者结合会导致训练发散。让我们用数学分析为什么会这样。

发散的数学机制

考虑线性函数逼近：，其中是特征向量。 Q-Learning 的参数更新是：

问题在于，目标依赖于——当我们更新时，目标也在移动（ moving target）。这就像射击一个移动的靶子，而且靶子的移动方向还取决于你的瞄准方向。

更糟糕的是，函数逼近会引入泛化：更新会影响到（如果和相似）。如果更新方向不一致，可能出现振荡：

更新使其增大 → 由于泛化，也增大
但的真实 Q 值较低 → 下次更新使其减小
再次泛化回，形成循环

Baird 在 1995 年构造了一个反例，展示了即使是简单的线性函数逼近+Q-Learning 也会发散。在他的"star counterexample"中， 7 个状态连接成星形结构，用 6 个特征表示，标准的 Q-Learning 更新会导致参数指数级爆炸。

早期尝试：神经拟合 Q 迭代（ NFQ）

在 DQN 之前， Riedmiller 在 2005 年提出了神经拟合 Q 迭代（ Neural Fitted Q-Iteration, NFQ）。它的思路是：

收集一批经验$(s,a,r,s') $用当前网络计算目标$ y = r + _{a'} Q(s',a') $用监督学习训练网络，最小化$ = (y - Q(s,a))^2$4. 重复步骤 1-3

NFQ 在一些简单任务上有效，但在 Atari 这样的高维环境中仍然不稳定。原因是： - 样本相关性：连续收集的经验高度相关（是的直接后继） - 分布非平稳：每次策略更新后，新收集的数据分布都会改变

DQN 的两大创新正是针对这两个问题。

DQN 的核心创新

经验回放（ Experience Replay）：打破相关性

经验回放的想法来自于监督学习中的"打乱数据"（ shuffling）。在监督学习中，如果按顺序训练（比如先训练所有猫的图片，再训练所有狗的图片），模型容易过拟合到数据的顺序，导致灾难性遗忘（ catastrophic forgetting）。解决方法是在每个 epoch 开始时随机打乱数据。

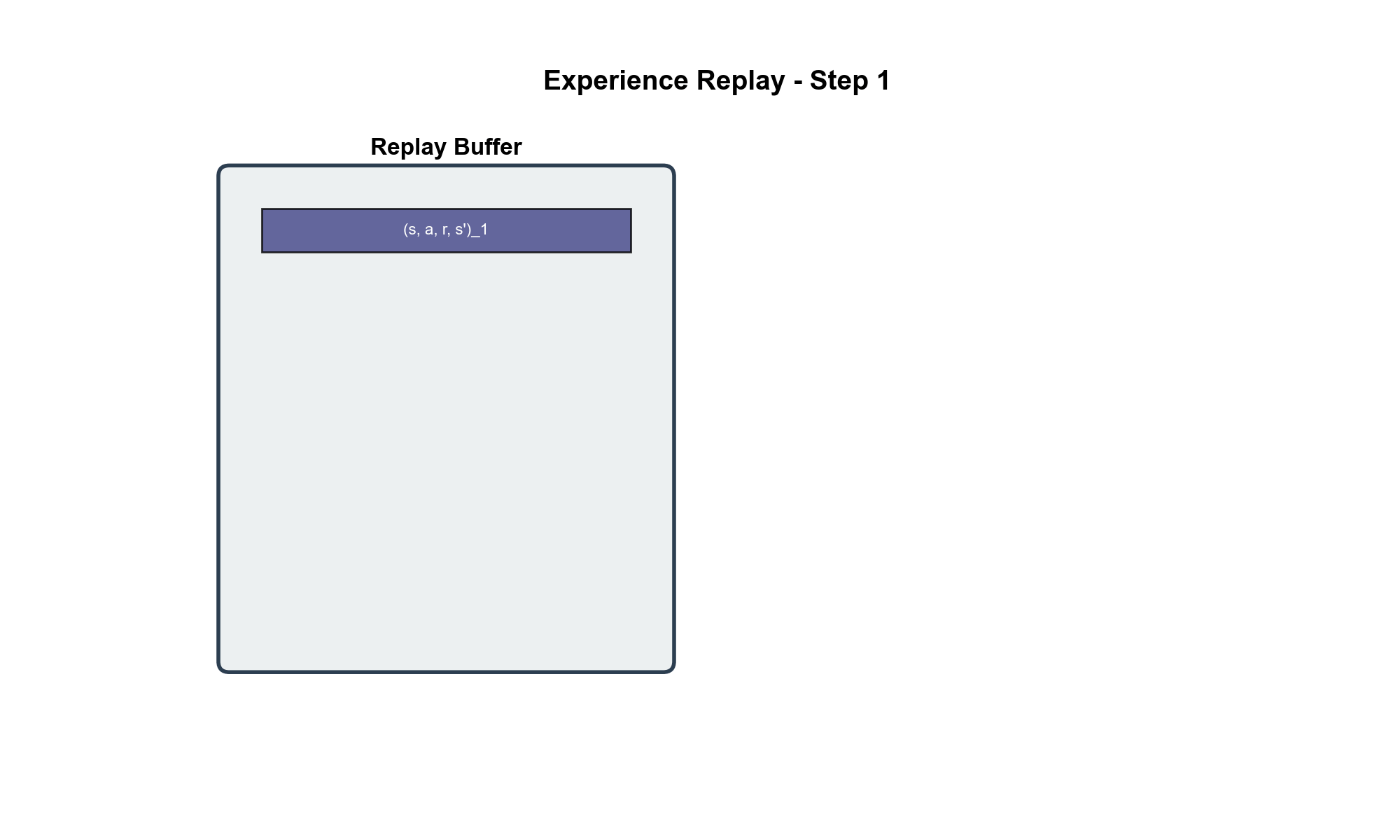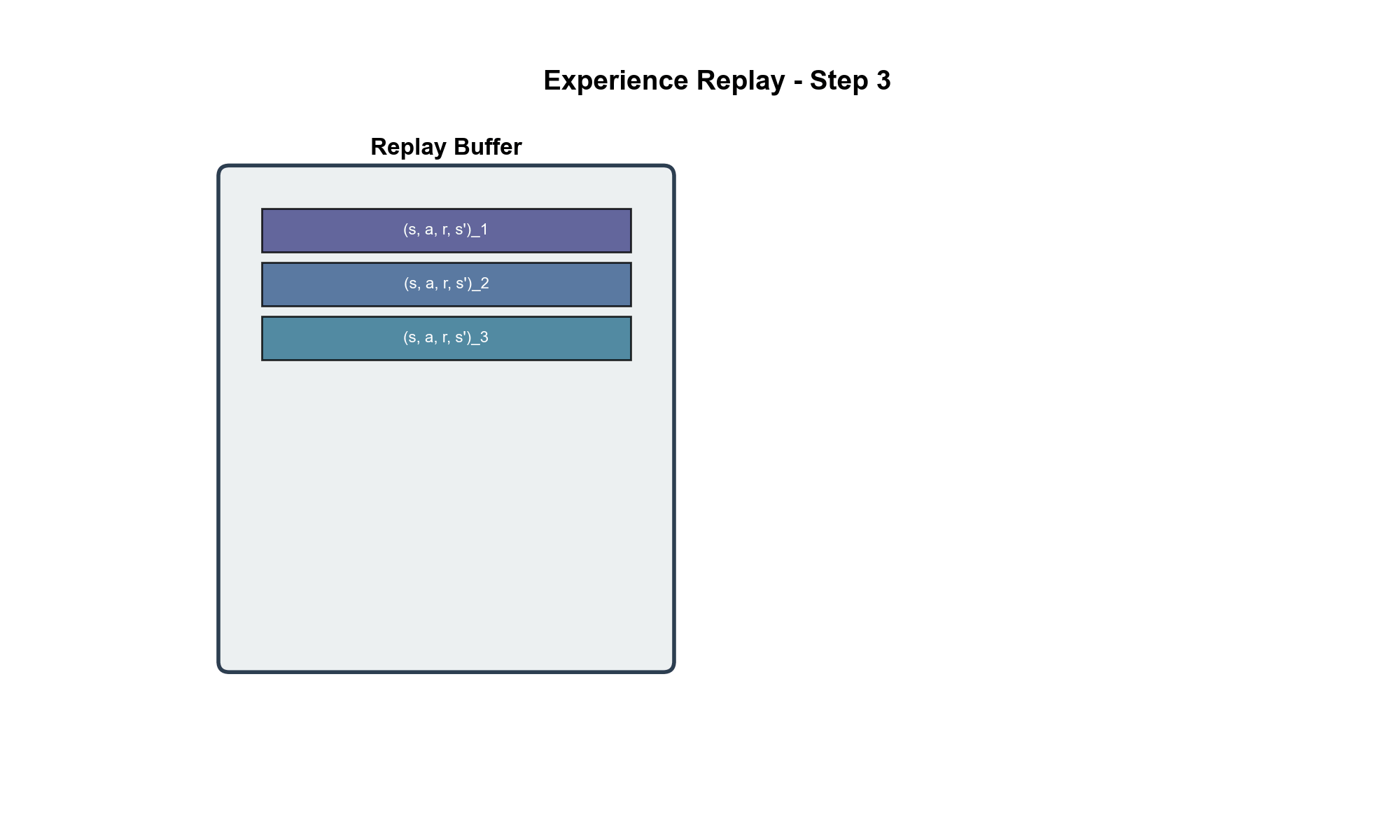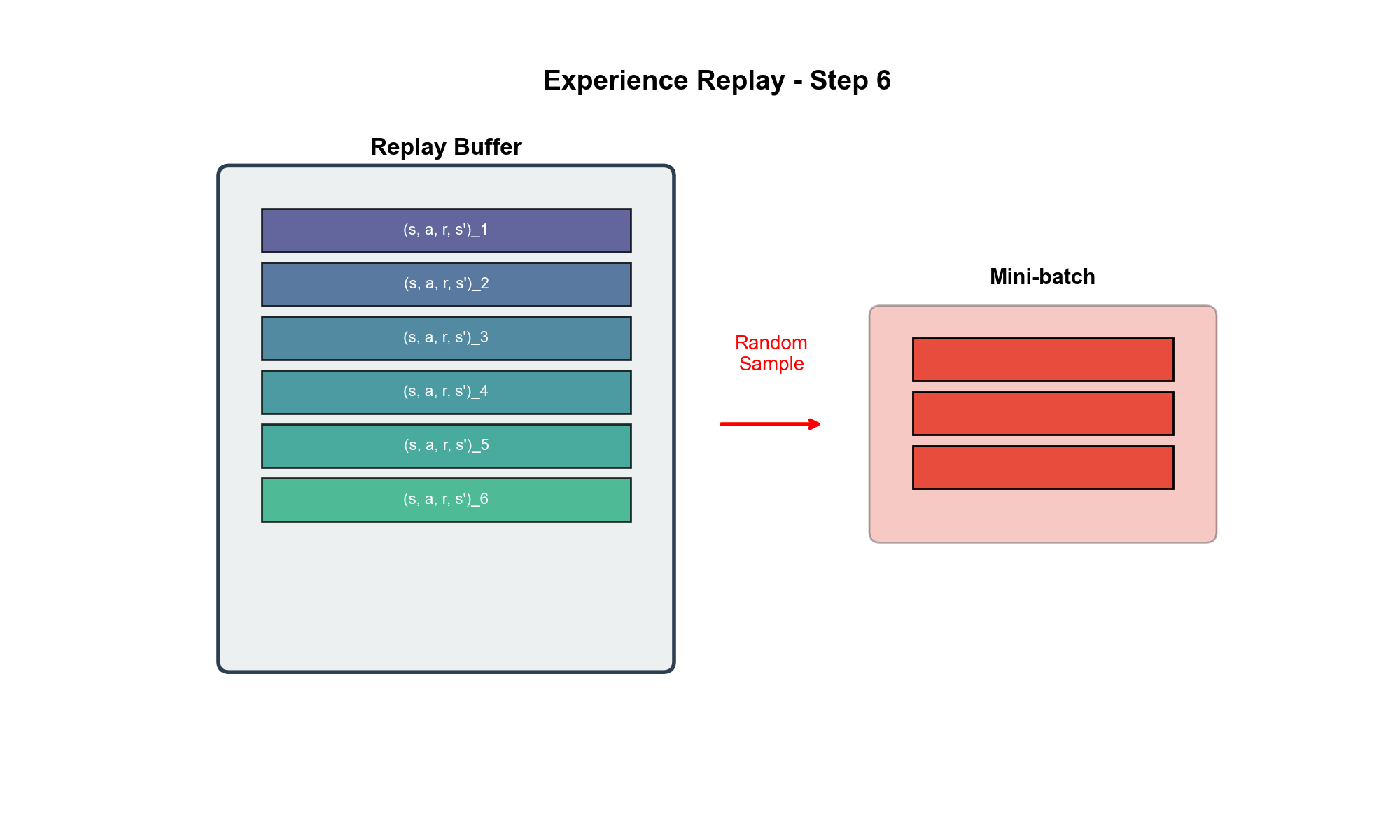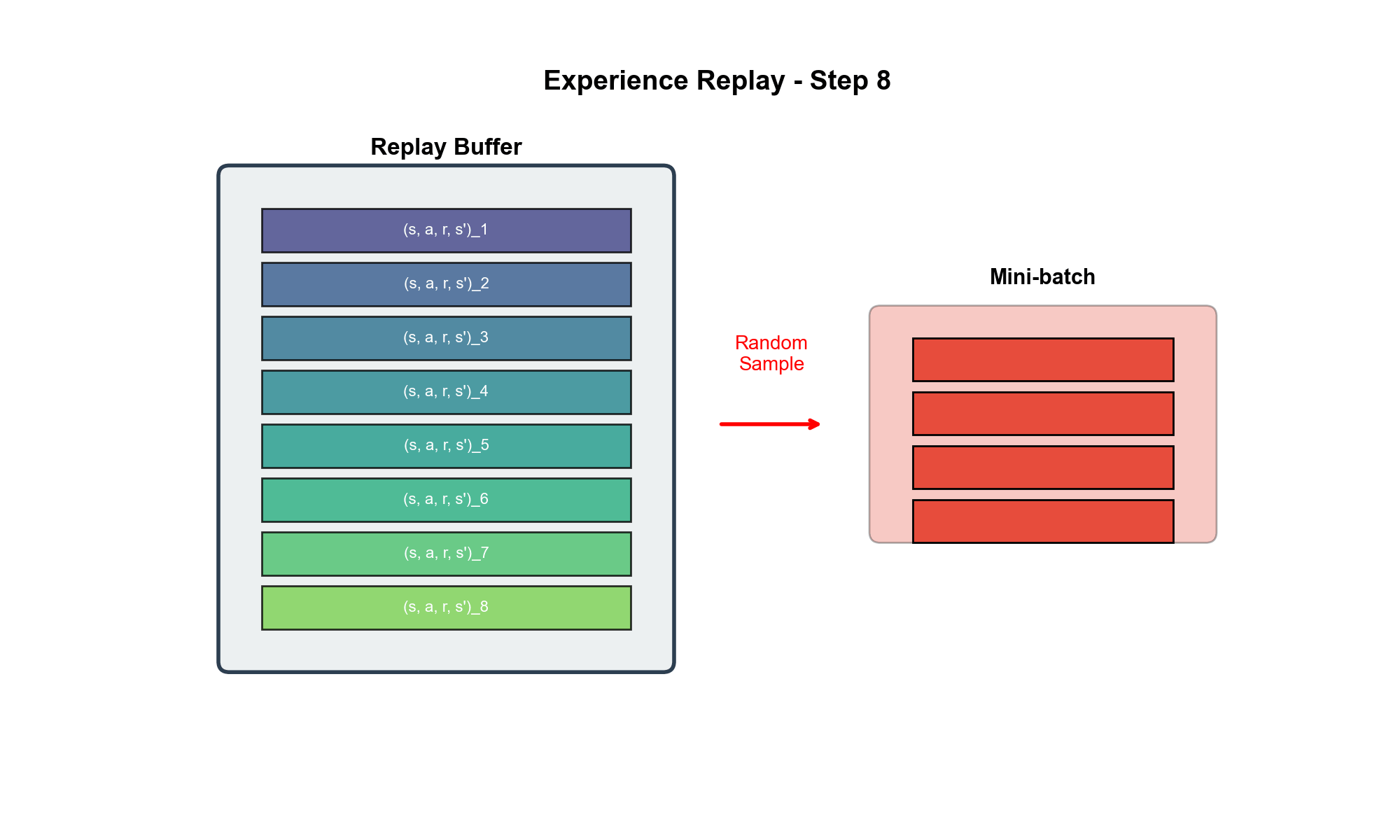
DQN 将这个思想应用到强化学习：

存储经验：维护一个回放缓冲区（ replay buffer），容量为（如 100 万）
添加经验：每次与环境交互得到后，将其存入$ $采样训练：每次更新时，从$ $ 中均匀随机采样一个小批量（如 32 条）
覆盖旧数据：当满时，新经验覆盖最旧的经验（ FIFO 队列）

这样做有三大好处：

好处 1：打破时间相关性

连续的经验和高度相关（共享）。如果用它们连续更新网络，梯度方向会非常相似，导致参数更新陷入局部模式。随机采样后，每个小批量中的样本来自不同时间步，相关性大大降低。

从信息论角度看，设连续样本的互信息为，随机采样后的期望互信息为：

$足够大$

这使得梯度估计的方差降低，训练更稳定。

好处 2：提高样本效率

在 on-policy 方法中，每条经验只能用一次（用完即扔）。而经验回放允许我们多次使用同一条经验——只要它还在 buffer 中，就可能被采样到。这对于样本昂贵的环境（比如机器人控制）特别重要。

设每条经验平均被使用次（取决于 buffer 大小和更新频率），样本效率提升约倍。在 DQN 的实现中，可以达到几十。

好处 3：平滑分布变化

策略更新时，新策略收集的数据分布会改变。但由于 buffer 中存储了大量旧策略的数据，当前训练用的数据分布是多个策略的混合，变化更加平滑。这避免了"急转弯"——一次策略更新导致数据分布剧变，进而导致下一次更新的目标完全不同。

数学上，设第次策略为，对应的状态分布为。 buffer 中的分布是：

d_{} _{i=k-N/m}^{k} d^{_i} $$

其中是每轮添加的新样本数。这个混合分布的变化率远小于单个的变化率。

实现细节： ReplayBuffer

import numpy as np
import random
from collections import deque

class ReplayBuffer:
    """
    经验回放缓冲区
    """
    def __init__(self, capacity=100000):
        self.buffer = deque(maxlen=capacity)
    
    def push(self, state, action, reward, next_state, done):
        """添加一条经验"""
        self.buffer.append((state, action, reward, next_state, done))
    
    def sample(self, batch_size):
        """随机采样一批经验"""
        batch = random.sample(self.buffer, batch_size)
        
        # 转换为 numpy 数组（方便 PyTorch 处理）
        states = np.array([x[0] for x in batch])
        actions = np.array([x[1] for x in batch])
        rewards = np.array([x[2] for x in batch])
        next_states = np.array([x[3] for x in batch])
        dones = np.array([x[4] for x in batch], dtype=np.float32)
        
        return states, actions, rewards, next_states, dones
    
    def __len__(self):
        return len(self.buffer)

这个实现用deque（双端队列）自动处理容量限制，新元素会挤掉最旧的元素。采样时用random.sample保证均匀性。

目标网络（ Target Network）：稳定移动目标

即使有了经验回放， DQN 仍然面临"移动目标"问题：更新参数会改变 TD 目标。目标网络的想法是：用一个独立的网络来计算目标，并定期同步。

具体来说， DQN 维护两个网络：

在线网络（ online network）：参数，用于选择动作和计算当前 Q 值
目标网络（ target network）：参数，仅用于计算 TD 目标

更新规则变为：

y = r + {a'} Q{^-}(s',a') () = _{(s,a,r,s') } $$

关键在于：在一定时间内（如 10000 步），保持不变，只有在更新。这样， TD 目标在这段时间内是固定的（或至少变化很慢），避免了"追逐移动靶子"的问题。

每隔步（如 10000），执行硬更新（ hard update）：

或者用软更新（ soft update），每步都执行：

DQN 原始论文使用硬更新，而后续很多算法（如 DDPG 、 SAC）使用软更新。软更新的好处是目标网络变化更平滑，但硬更新实现更简单。

理论分析：为什么目标网络有效

考虑 TD 误差的期望：

如果目标和当前用同一个网络（同一套参数），那么每次更新时： - 增大（朝目标方向） - 但也会改变（由于泛化），导致目标移动

两者的变化可能相互抵消，导致更新无效。更糟糕的是，如果的变化比更大（比如的特征与其他状态更相似），可能出现振荡。

目标网络切断了这个反馈循环：在固定的时间段内，目标只依赖于数据，不依赖于当前参数。这将强化学习的 bootstrapping 更新转化为类似监督学习的"固定目标"更新，稳定性大幅提升。

从优化角度看，固定目标网络相当于将目标函数的 Hessian 矩阵中的某些项置零（与相关的二阶导数），降低了优化表面的曲率，使梯度下降更容易收敛。

DQN 算法完整解析

伪代码与流程

现在我们可以写出完整的 DQN 算法：

算法： Deep Q-Network (DQN)

输入： - 环境 - Q 网络架构 - 回放缓冲区容量 - 批量大小 - 学习率 - 折扣因子 - 探索率${} , {} , {} $ - 目标网络更新频率输出：训练好的 Q 网络参数$ $初始化回放缓冲区$ $（容量$ N $）随机初始化网络参数$ $初始化目标网络参数$ ^- = 1, 2, , M$do 5. 初始化状态6. for do 7. 以概率选择随机动作，否则$a_t = a Q(s_t, a)$8. 执行，观察$r_t, s{t+1}, $9. 存储转移到$$10. 从中随机采样一批（大小） 11. 计算目标：$y_i = r_i + (1 - i) {a'} Q_{^-}(s'i, a')$12. 计算损失：$() = i (y_i - Q(s_i, a_i))^2$13. 梯度下降更新：$- ()$14. 每步更新目标网络：15. 衰减探索率：$({} , {} )$16. if then break 17. end for

几个关键点：

第 11 行：确保终止状态的目标为（没有未来回报）
第 10 行：只有当时才开始训练（预填充 buffer）
探索率衰减：初期鼓励探索，逐渐衰减到偏向利用

损失函数与梯度计算

DQN 的损失函数是均方 TD 误差：

对求梯度：

注意： 1. 目标被视为常数（ detach），不参与梯度计算 2. 只有的梯度被保留

这与监督学习的回归损失完全一致，只是这里的"真实标签" 是自己估计出来的（ bootstrapping）。

训练技巧

梯度裁剪（ Gradient Clipping）

Atari 环境的奖励范围很大（比如 Breakout 的砖块得分可以累积到几百），导致 TD 误差也很大，梯度可能爆炸。 DQN 使用梯度裁剪：

PyTorch 中可以用torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=10)。

学习率调度（ Learning Rate Schedule）

DQN 通常使用固定学习率（如），但在某些任务中，使用余弦退火或指数衰减可以提升后期性能：

奖励裁剪与归一化

Atari 游戏的奖励尺度差异很大（ Pong 是-1/0/+1， Breakout 可以到几百）。 DQN 论文对所有正奖励裁剪到+1，负奖励裁剪到-1：

r_{} = (r) $$

这使得不同游戏可以用相同的超参数。但代价是丢失了奖励的幅度信息——在某些任务中可能不合适。

完整 Atari DQN 实现

下面是一个完整的 DQN 实现，用于 Atari Pong 游戏（约 350 行代码）：

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import numpy as np
import random
from collections import deque
import gym

# ===== 神经网络架构 =====
class DQN(nn.Module):
    """
    DQN 网络： 3 个卷积层 + 2 个全连接层
    输入： 84x84x4 的状态（ 4 帧灰度图像栈）
    输出：每个动作的 Q 值
    """
    def __init__(self, n_actions):
        super(DQN, self).__init__()
        self.conv1 = nn.Conv2d(4, 32, kernel_size=8, stride=4)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=4, stride=2)
        self.conv3 = nn.Conv2d(64, 64, kernel_size=3, stride=1)
        self.fc1 = nn.Linear(64 * 7 * 7, 512)
        self.fc2 = nn.Linear(512, n_actions)
    
    def forward(self, x):
        # x: (batch, 4, 84, 84)
        x = F.relu(self.conv1(x))  # -> (batch, 32, 20, 20)
        x = F.relu(self.conv2(x))  # -> (batch, 64, 9, 9)
        x = F.relu(self.conv3(x))  # -> (batch, 64, 7, 7)
        x = x.view(x.size(0), -1)  # flatten
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

# ===== 经验回放缓冲区 =====
class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = deque(maxlen=capacity)
    
    def push(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))
    
    def sample(self, batch_size):
        batch = random.sample(self.buffer, batch_size)
        states, actions, rewards, next_states, dones = zip(*batch)
        return (np.array(states), np.array(actions), 
                np.array(rewards), np.array(next_states), 
                np.array(dones, dtype=np.float32))
    
    def __len__(self):
        return len(self.buffer)

# ===== DQN 智能体 =====
class DQNAgent:
    def __init__(self, n_actions, device='cuda'):
        self.n_actions = n_actions
        self.device = device
        
        # 初始化网络
        self.policy_net = DQN(n_actions).to(device)
        self.target_net = DQN(n_actions).to(device)
        self.target_net.load_state_dict(self.policy_net.state_dict())
        self.target_net.eval()  # 目标网络不需要训练
        
        # 优化器
        self.optimizer = optim.Adam(self.policy_net.parameters(), lr=2.5e-4)
        
        # 回放缓冲区
        self.memory = ReplayBuffer(capacity=100000)
        
        # 超参数
        self.gamma = 0.99
        self.batch_size = 32
        self.epsilon_start = 1.0
        self.epsilon_end = 0.01
        self.epsilon_decay = 0.995
        self.epsilon = self.epsilon_start
        self.target_update_freq = 10000
        self.steps_done = 0
    
    def select_action(self, state, training=True):
        """选择动作（ epsilon-greedy）"""
        if training and random.random() < self.epsilon:
            return random.randrange(self.n_actions)
        else:
            with torch.no_grad():
                state_t = torch.FloatTensor(state).unsqueeze(0).to(self.device)
                q_values = self.policy_net(state_t)
                return q_values.argmax(dim=1).item()
    
    def train_step(self):
        """执行一次训练更新"""
        if len(self.memory) < self.batch_size:
            return None
        
        # 采样一批经验
        states, actions, rewards, next_states, dones = self.memory.sample(self.batch_size)
        
        # 转换为 tensor
        states = torch.FloatTensor(states).to(self.device)
        actions = torch.LongTensor(actions).to(self.device)
        rewards = torch.FloatTensor(rewards).to(self.device)
        next_states = torch.FloatTensor(next_states).to(self.device)
        dones = torch.FloatTensor(dones).to(self.device)
        
        # 当前 Q 值： Q(s, a)
        current_q = self.policy_net(states).gather(1, actions.unsqueeze(1)).squeeze(1)
        
        # 目标 Q 值： r + gamma * max_a' Q_target(s', a')
        with torch.no_grad():
            next_q = self.target_net(next_states).max(1)[0]
            target_q = rewards + (1 - dones) * self.gamma * next_q
        
        # 计算损失
        loss = F.mse_loss(current_q, target_q)
        
        # 反向传播
        self.optimizer.zero_grad()
        loss.backward()
        # 梯度裁剪
        torch.nn.utils.clip_grad_norm_(self.policy_net.parameters(), max_norm=10)
        self.optimizer.step()
        
        # 更新步数
        self.steps_done += 1
        
        # 更新目标网络
        if self.steps_done % self.target_update_freq == 0:
            self.target_net.load_state_dict(self.policy_net.state_dict())
        
        # 衰减 epsilon
        if self.epsilon > self.epsilon_end:
            self.epsilon *= self.epsilon_decay
        
        return loss.item()
    
    def save(self, path):
        torch.save(self.policy_net.state_dict(), path)
    
    def load(self, path):
        self.policy_net.load_state_dict(torch.load(path))
        self.target_net.load_state_dict(self.policy_net.state_dict())

# ===== 环境包装器（预处理）=====
class AtariPreprocessing:
    """Atari 环境预处理：灰度化、缩放、帧栈"""
    def __init__(self, env, frame_stack=4):
        self.env = env
        self.frame_stack = frame_stack
        self.frames = deque(maxlen=frame_stack)
    
    def reset(self):
        obs = self.env.reset()
        obs = self._preprocess(obs)
        for _ in range(self.frame_stack):
            self.frames.append(obs)
        return self._get_state()
    
    def step(self, action):
        obs, reward, done, info = self.env.step(action)
        obs = self._preprocess(obs)
        self.frames.append(obs)
        return self._get_state(), np.sign(reward), done, info
    
    def _preprocess(self, frame):
        """灰度化并缩放到 84x84"""
        frame = frame[34:194]  # 裁剪 Pong 的上下边界
        frame = frame[::2, ::2, 0]  # 下采样并取单通道
        frame = frame / 255.0
        return frame
    
    def _get_state(self):
        """返回 4 帧栈"""
        return np.array(self.frames)

# ===== 训练循环 =====
def train_dqn(env_name='PongNoFrameskip-v4', n_episodes=1000, device='cuda'):
    # 创建环境
    env = gym.make(env_name)
    env = AtariPreprocessing(env)
    n_actions = env.env.action_space.n
    
    # 创建智能体
    agent = DQNAgent(n_actions, device=device)
    
    # 训练统计
    episode_rewards = []
    episode_losses = []
    
    for episode in range(n_episodes):
        state = env.reset()
        total_reward = 0
        losses = []
        
        while True:
            # 选择动作
            action = agent.select_action(state)
            
            # 执行动作
            next_state, reward, done, _ = env.step(action)
            total_reward += reward
            
            # 存储经验
            agent.memory.push(state, action, reward, next_state, done)
            
            # 训练
            loss = agent.train_step()
            if loss is not None:
                losses.append(loss)
            
            state = next_state
            
            if done:
                break
        
        episode_rewards.append(total_reward)
        avg_loss = np.mean(losses) if losses else 0
        episode_losses.append(avg_loss)
        
        # 打印进度
        if (episode + 1) % 10 == 0:
            avg_reward = np.mean(episode_rewards[-10:])
            print(f"Episode {episode+1}, Avg Reward: {avg_reward:.2f}, "
                  f"Epsilon: {agent.epsilon:.3f}, Loss: {avg_loss:.4f}")
        
        # 保存模型
        if (episode + 1) % 100 == 0:
            agent.save(f'dqn_pong_{episode+1}.pth')
    
    return agent, episode_rewards, episode_losses

# ===== 运行训练 =====
if __name__ == '__main__':
    device = 'cuda' if torch.cuda.is_available() else 'cpu'
    print(f"Using device: {device}")
    
    agent, rewards, losses = train_dqn(n_episodes=1000, device=device)
    
    # 可视化
    import matplotlib.pyplot as plt
    
    plt.figure(figsize=(12, 5))
    
    plt.subplot(1, 2, 1)
    plt.plot(rewards, alpha=0.3)
    plt.plot(np.convolve(rewards, np.ones(50)/50, mode='valid'), linewidth=2)
    plt.xlabel('Episode')
    plt.ylabel('Total Reward')
    plt.title('Training Rewards')
    plt.grid(True)
    
    plt.subplot(1, 2, 2)
    plt.plot(losses, alpha=0.3)
    plt.plot(np.convolve(losses, np.ones(50)/50, mode='valid'), linewidth=2)
    plt.xlabel('Episode')
    plt.ylabel('Loss')
    plt.title('Training Loss')
    plt.grid(True)
    
    plt.tight_layout()
    plt.savefig('dqn_training.png')
    plt.show()

这段代码包含了 DQN 的所有关键组件：卷积神经网络、经验回放、目标网络、 epsilon-greedy 探索、梯度裁剪。在 Pong 游戏上训练约 200-300 个 episode 后，智能体通常能达到接近最优的表现（平均奖励接近+21，即每局赢 21 分）。

DQN 变体：从 Double 到 Rainbow

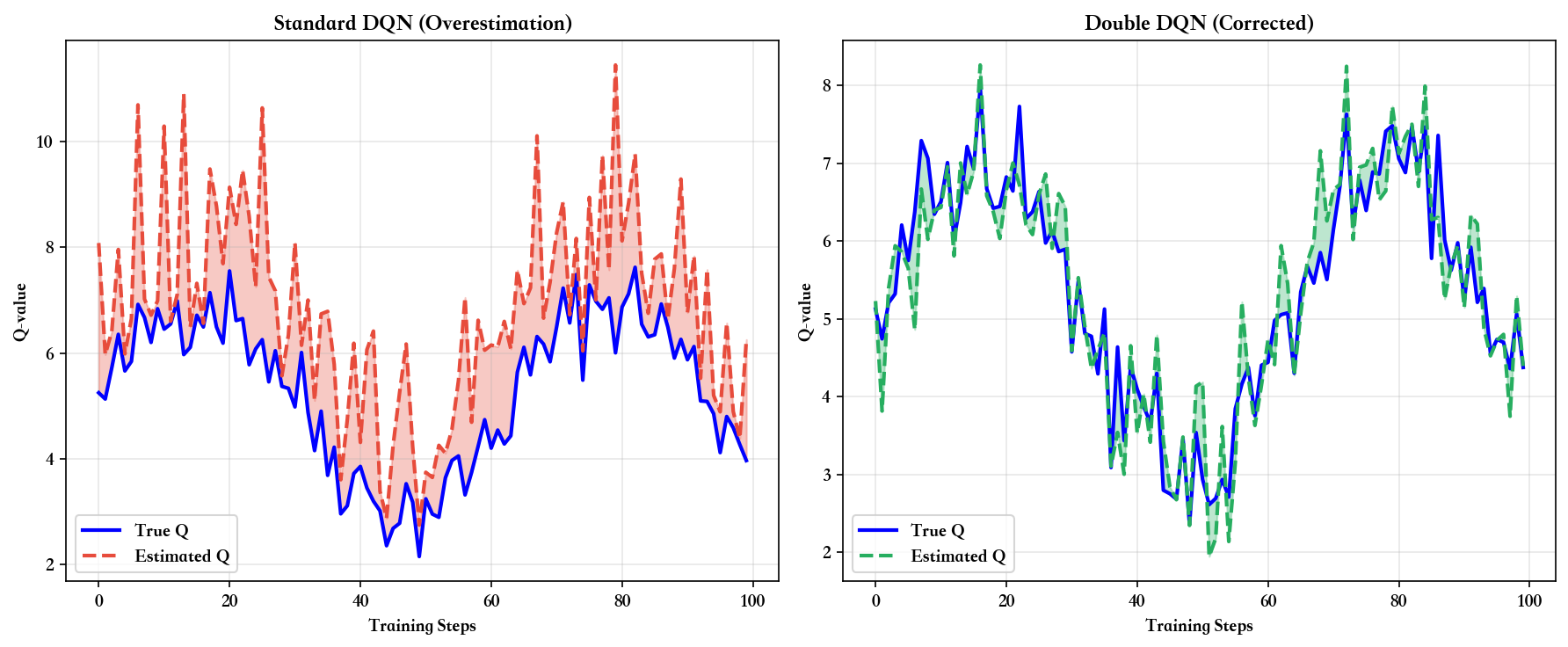
Double DQN：解决 Q 值过估计

问题：操作的正偏差

DQN 的更新目标中的操作会导致系统性的过估计（ overestimation）。原因是：

设真实 Q 值为，我们的估计为，其中是估计误差（零均值）。那么：

即使，由于取了最大值，偏向于选择误差为正的动作：

这个不等式是 Jensen 不等式（对于凸函数）。过估计会累积：当前状态的过估计会传播到前一状态，形成正反馈循环。

解决方案：解耦选择与评估

Double DQN（ van Hasselt et al., 2016）的思想是：用在线网络选择动作，用目标网络评估该动作的价值。更新目标变为：

y^{} = r + Q_{^-}(s', {a'} Q(s',a')) $$

注意到用的是（在线网络），但评估用的是（目标网络）。这样，即使在线网络高估了某个动作，目标网络不太可能同时高估同一个动作（两个网络的误差不相关），偏差被削弱。

数学上，设两个独立估计的误差为（独立同分布），那么：

因为与的选择无关（独立性），期望仍为零。

数值示例

考虑一个状态有 3 个动作，真实 Q 值为，估计误差为：

DQN：（高估 2）
Double DQN：在线网络选择动作 2（ Q=12），目标网络评估为（假设目标网络的误差），得到 9.5（更接近真实值）

实现

只需修改一行代码：

# DQN 原始目标
with torch.no_grad():
    next_q = self.target_net(next_states).max(1)[0]  # 用目标网络选择+评估
    target_q = rewards + (1 - dones) * self.gamma * next_q

# Double DQN 目标
with torch.no_grad():
    next_actions = self.policy_net(next_states).argmax(1)  # 在线网络选择
    next_q = self.target_net(next_states).gather(1, next_actions.unsqueeze(1)).squeeze(1)  # 目标网络评估
    target_q = rewards + (1 - dones) * self.gamma * next_q

实验表明， Double DQN 在多数 Atari 游戏上都能减少过估计，提升稳定性和最终性能。

Dueling DQN：分离状态价值与优势

动机：不是所有状态都需要关心动作

考虑 Atari 游戏中的两种场景： 1. 紧急情况（比如 Pong 中球即将错过）：选择哪个动作至关重要 2. 平淡时刻（比如球远离挡板）：无论选什么动作，价值都差不多

传统 DQN 用同一个网络头输出所有，需要同时学习"这个状态好不好"和"各个动作的相对优劣"。 Dueling DQN 将两者分离：

Q(s,a) = V(s) + A(s,a) $$

其中： - ：状态价值（ state value），衡量在下的期望回报，与动作无关 - ：优势函数（ advantage），衡量动作相对于平均动作的优劣

直觉上，回答"这个状态有多好"，回答"这个动作比平均水平好多少"。

可识别性问题

直接分离和有一个问题：给定，分解不唯一。比如可以分解为，也可以是。为了唯一性，强制优势函数的均值为 0：

Q(s,a) = V(s) + ( A(s,a) - _{a'} A(s,a') ) $$

或者用最大优势为 0（实践中更常用）：

Q(s,a) = V(s) + ( A(s,a) - _{a'} A(s,a') ) $$

这样，最优动作的为 0，就等于。

网络架构

Dueling DQN 的卷积层与 DQN 相同，但全连接层分为两个流（ stream）：

class DuelingDQN(nn.Module):
    def __init__(self, n_actions):
        super(DuelingDQN, self).__init__()
        # 共享卷积层
        self.conv1 = nn.Conv2d(4, 32, kernel_size=8, stride=4)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=4, stride=2)
        self.conv3 = nn.Conv2d(64, 64, kernel_size=3, stride=1)
        
        # 价值流
        self.value_fc = nn.Linear(64 * 7 * 7, 512)
        self.value_head = nn.Linear(512, 1)
        
        # 优势流
        self.advantage_fc = nn.Linear(64 * 7 * 7, 512)
        self.advantage_head = nn.Linear(512, n_actions)
    
    def forward(self, x):
        # 共享特征提取
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        x = F.relu(self.conv3(x))
        x = x.view(x.size(0), -1)
        
        # 价值流
        value = F.relu(self.value_fc(x))
        value = self.value_head(value)  # (batch, 1)
        
        # 优势流
        advantage = F.relu(self.advantage_fc(x))
        advantage = self.advantage_head(advantage)  # (batch, n_actions)
        
        # 组合： Q = V + (A - mean(A))
        q_values = value + (advantage - advantage.mean(dim=1, keepdim=True))
        return q_values

为什么有效

Dueling 架构的优势在于价值函数的学习更高效。在很多状态下，动作的选择对价值影响很小——此时可以从所有动作的经验中学习（数据共享），而不是每个单独学习。这相当于引入了归纳偏置（ inductive bias）：告诉网络"先学会评估状态好坏，再学细节"。

实验表明， Dueling DQN 在需要长期规划的任务（如 Seaquest 、 Enduro）中提升明显，因为这些任务中状态价值的差异更重要。

Prioritized Experience Replay：重要性采样

问题：并非所有经验同等重要

均匀随机采样的经验回放假设所有经验同等重要，但直觉上： - TD 误差大的经验更"出乎意料"，包含更多信息 - TD 误差小的经验已经被学得很好，重复训练意义不大

Prioritized Experience Replay（ PER， Schaul et al., 2016）根据 TD 误差的大小来分配采样概率。

优先级定义

每条经验的优先级定义为：

p_i = |_i| + $$

其中是 TD 误差，是小常数（避免优先级为 0）。采样概率为：

P(i) = $$

其中控制优先级的强度（退化为均匀采样，完全按优先级）。

重要性采样权重

Prioritized 采样改变了数据分布，会引入偏差。为了修正，使用重要性采样权重：

w_i = ( )^ $$

并归一化：。损失函数变为加权版本：

从 0.4 逐渐退火到 1.0（初期偏差修正较弱，后期完全修正）。

实现

需要维护一个优先级队列，可以用 SumTree 数据结构实现的采样和更新：

class PrioritizedReplayBuffer:
    def __init__(self, capacity, alpha=0.6):
        self.capacity = capacity
        self.alpha = alpha
        self.buffer = []
        self.priorities = np.zeros(capacity, dtype=np.float32)
        self.position = 0
    
    def push(self, transition):
        max_priority = self.priorities.max() if self.buffer else 1.0
        
        if len(self.buffer) < self.capacity:
            self.buffer.append(transition)
        else:
            self.buffer[self.position] = transition
        
        self.priorities[self.position] = max_priority
        self.position = (self.position + 1) % self.capacity
    
    def sample(self, batch_size, beta=0.4):
        N = len(self.buffer)
        priorities = self.priorities[:N]
        
        # 计算采样概率
        probs = priorities ** self.alpha
        probs /= probs.sum()
        
        # 采样索引
        indices = np.random.choice(N, batch_size, p=probs)
        
        # 计算重要性采样权重
        weights = (N * probs[indices]) ** (-beta)
        weights /= weights.max()
        
        # 提取经验
        batch = [self.buffer[i] for i in indices]
        
        return batch, indices, weights
    
    def update_priorities(self, indices, td_errors):
        """更新 TD 误差对应的优先级"""
        for idx, td_error in zip(indices, td_errors):
            self.priorities[idx] = abs(td_error) + 1e-6

PER 在样本效率上有显著提升，但实现复杂度更高，训练时间也略有增加。

其他 Rainbow 组件

Noisy Networks：用可学习的噪声替代-greedy 探索。在权重中加入噪声参数：

w = + , (0, I) $$

其中都是可学习的。这样探索策略也能通过梯度优化。

Multi-step Learning：用 n-step return 替代 1-step TD 目标：

y^{(n)} = {t=0}^{n-1} ^t r{t} + ^n _{a'} Q(s_n, a') $$

n-step 能更快传播奖励信号，但方差也更大（典型取）。

Distributional RL (C51)：不学习 Q 值的期望，而是学习整个分布。将值域离散化为 51 个桶（ bins），用交叉熵损失训练分布预测。这能捕捉风险（方差）信息，在探索中更有利。

Rainbow：将以上 6 种技术（ Double DQN 、 Dueling 、 PER 、 Noisy Nets 、 Multi-step 、 C51）全部组合，在 Atari 上达到当时的 SOTA 性能。消融实验表明，每种技术都有贡献，且组合效果超过单独叠加（协同作用）。

理论分析

经验回放的理论保证

从优化角度看，经验回放相当于从经验分布中采样，而不是从即时策略中采样。设当前策略对应的状态分布为， buffer 中的混合分布为。训练目标是最小化：

J() = _{(s,a) {d}} $$

如果（ buffer 覆盖了最优策略的分布），那么收敛点是最优 Q 函数。但实际上是多个策略的混合，可能与偏差较大——这是 off-policy 方法的固有问题。

好消息是， Munos 等人（ 2016）证明了：如果 replay buffer 中的数据满足一定的覆盖性条件（ coverage），且目标网络更新足够慢， DQN 仍然能以一定概率收敛到近似最优解，误差界为，其中${} $是函数逼近误差，$ {} $ 是采样误差。

目标网络的方差分析

目标网络的作用可以从方差-偏差权衡来理解。考虑 TD 目标的方差：

如果在快速变化（每步都更新），会很大。固定目标网络在步内不变，方差大幅降低：

代价是引入了偏差：是过时的参数，目标不是完全准确。但实验表明，这个偏差远小于方差降低带来的好处。

数学上，可以用 Bellman 误差的期望来量化：

其中是 Bellman 算子，是用固定参数的算子。第二项的方差更小，更容易优化。

实战技巧与调试

超参数选择

超参数	典型值	说明
`buffer_size`	100k-1M	越大越好，但内存有限； Atari 用 1M
`batch_size`	32-128	太小不稳定，太大训练慢； 32 是常见选择
`learning_rate`	1e-4 到 1e-3	Adam 优化器通常用 2.5e-4
`gamma`	0.99	折扣因子，长期任务用 0.99，短期任务可用 0.9
`epsilon_start`	1.0	初始探索率
`epsilon_end`	0.01-0.1	最终探索率， 0.01 适合 Atari
`epsilon_decay`	0.995	每轮衰减因子，或用线性衰减
`target_update_freq`	1k-10k	目标网络更新频率， 10k 步是常见选择

调参建议： 1. 先用较小的buffer_size和较大的learning_rate快速验证代码正确性 2. 确认 loss 在下降、 reward 在上升后，再用完整超参数长时间训练 3. 如果训练不稳定（ loss 振荡、 reward 崩溃），减小learning_rate或增大target_update_freq

训练曲线分析

正常曲线： reward 逐渐上升， loss 先上升后下降 - 初期（ 0-100 episodes）： reward 接近随机水平， loss 上升（因为 Q 值从 0 开始增长， TD 误差变大） - 中期（ 100-500 episodes）： reward 快速提升， loss 达到峰值后下降（ Q 值趋于稳定） - 后期（ 500+ episodes）： reward 收敛到接近最优， loss 稳定在低水平

异常现象： - Loss 爆炸：突然增大到 1e3 甚至 1e6 - 原因：梯度爆炸或 Q 值发散 - 解决：检查梯度裁剪，降低学习率，检查奖励是否未归一化 - Reward 崩溃：先上升后突然下降并不再恢复 - 原因：灾难性遗忘或陷入局部最优 - 解决：增大 buffer_size，降低学习率，检查目标网络更新是否过于频繁 - Reward 不涨：长时间停留在随机水平 - 原因：探索不足或网络容量不够 - 解决：增大 epsilon 或延长 epsilon_decay，检查网络架构

调试技巧

1. 监控 Q 值分布

在训练过程中打印 Q 值的统计量：

with torch.no_grad():
    q_values = agent.policy_net(states)
    print(f"Q mean: {q_values.mean():.2f}, Q std: {q_values.std():.2f}, "
          f"Q max: {q_values.max():.2f}, Q min: {q_values.min():.2f}")

正常情况下， Q 值应该逐渐增大并稳定。如果 Q 值持续爆炸（如超过 1000），说明有问题。

2. 检查 TD 误差

打印 TD 误差的分布：

1 2	td_errors = (target_q - current_q).abs() print(f"TD error mean: {td_errors.mean():.4f}, max: {td_errors.max():.4f}")

TD 误差应该逐渐减小。如果长期停留在高位，说明网络没有学到有用的模式。

3. 可视化动作分布

统计智能体选择各个动作的频率：

action_counts = np.zeros(n_actions)
for _ in range(100):
    action = agent.select_action(state, training=False)
    action_counts[action] += 1
print("Action distribution:", action_counts / 100)

如果某个动作从不被选择，可能是网络陷入了局部最优。

4. 简化环境测试

在复杂环境（如 Atari）调试时，先在简单环境（如 CartPole）上验证代码正确性：

1 2	env = gym.make('CartPole-v1') # CartPole 应该在 100-200 episodes 内解决（平均 reward > 195）

如果简单环境都不 work，说明代码有 bug 。

深度 Q&A

Q1：为什么 DQN 用 off-policy 而不是 on-policy？

A： Off-policy 的核心优势是数据利用效率。 On-policy 方法（如 SARSA 、 A3C）要求训练数据必须来自当前策略——每次更新策略后，旧数据就作废了。而 off-policy 方法（如 Q-Learning 、 DQN）可以使用任意策略收集的数据，只要它探索了相关的状态-动作对。

DQN 的经验回放正是利用了这一点： buffer 中的数据来自过去的多个策略（），但都可以用来更新当前策略。这使得每条经验可以被重复使用几十次，样本效率提升巨大。

代价是 off-policy 方法更难收敛（因为数据分布与目标策略不匹配），需要额外的稳定化技术（如目标网络）。但在样本昂贵的场景（如机器人、 Atari），这个 trade-off 是值得的。

Q2：经验回放的 buffer 大小如何选择？

A： Buffer 大小的选择需要平衡三个因素：

覆盖性：越大， buffer 覆盖的状态分布越广， off-policy 偏差越小
新鲜度：越小， buffer 中的数据越"新鲜"，越接近当前策略
内存限制：存储需要内存， Atari 的 84x84x4 图像占用约 28KB

典型选择： - Atari： 1M（约 28GB 内存） - 简单环境（如 CartPole）： 10k-100k - 连续控制（如 MuJoCo）： 100k-1M

经验法则： buffer 应该能容纳至少 100 个完整 episode 的数据。如果太小（如只有 10 个 episode）， buffer 会频繁被覆盖，样本多样性不足。

实验建议：先用较小的 buffer（如 10k）快速迭代，确认代码正确后再用大 buffer 训练。

Q3： Double DQN 解决的过估计问题有多严重？

A：在很多 Atari 游戏中， DQN 的 Q 值过估计非常显著。 van Hasselt 等人在论文中展示了一个例子：

Pong 游戏：真实 Q 值范围约为-21 到+21（游戏得分）
DQN 估计： Q 值逐渐膨胀到+50 甚至+100
Double DQN 估计：稳定在-21 到+21 附近

过估计的严重性取决于环境的随机性和动作空间大小： - 随机性大（如噪声奖励）→ 估计误差大 → 过估计严重 - 动作多（如 18 个动作）→ 操作的偏差大 → 过估计严重

在某些游戏中（如 Seaquest），过估计会导致智能体选择次优策略——因为某些"看起来很好"的动作（ Q 值被高估）实际上很差。 Double DQN 通过解耦选择与评估，能减少 50%-90%的过估计偏差。

但也有例外：在确定性环境（如下棋）中，过估计问题较轻， Double DQN 的提升有限。

Q4： Dueling DQN 在什么场景下效果最好？

A： Dueling DQN 在动作的影响差异小的场景中提升最大。具体包括：

长期规划任务（如 Seaquest 、 Enduro）：大部分时间在"巡航"，只有少数关键时刻需要精确动作。状态价值比优势更重要。
动作冗余度高（如 Atari 中某些动作几乎等价）：比如"向左"和"向左+射击"在没有敌人时效果相同。 Dueling 能自动识别这种冗余，集中学习。
稀疏奖励环境：在大部分状态下，所有动作的 Q 值都接近（因为奖励稀疏），此时接近 0，承载了主要信息。

反例：在动作差异大的环境（如格斗游戏，每个动作都至关重要）中， Dueling 的优势不明显，因为优势函数本身就很复杂，分离并没有简化学习。

Q5： Rainbow 为什么不是简单的 1+1=2？

A： Rainbow 的性能提升并非各技术的简单叠加，而是有协同作用（ synergy）。消融实验表明：

单独的 Double DQN：提升 30%
单独的 Dueling DQN：提升 20%
两者组合：提升 60%（大于 30%+20%）

原因是： - Double DQN 减少过估计 → Dueling 的更准确 → 优势的学习更稳定 - PER 优先训练重要样本 → 加速 Double DQN 的过估计修正 → 更快收敛 - Multi-step Learning 加速信用分配 → 配合 Distributional RL 捕捉不确定性 → 探索更高效

但也有负面交互： PER 的重要性采样权重会增大梯度方差，需要更小的学习率； Noisy Networks 的探索噪声可能与 Multi-step 的方差冲突。 Rainbow 的成功在于精心调整了这些组件的超参数，使协同效应最大化。

Q6： DQN 为什么不能处理连续动作空间？

A： DQN 的核心操作是和，需要遍历所有动作。在离散动作空间（如 Atari 的 18 个动作），这很简单——网络输出 18 个 Q 值，取最大。

但在连续动作空间（如机器人关节角度），操作变成一个优化问题：

没有解析解，需要用优化算法（如梯度上升、遗传算法）求解。这不仅计算昂贵，还会引入额外的近似误差。

解决方案： - 离散化：将连续动作空间划分为网格（如 10x10），但维度灾咒会导致组合爆炸 - Actor-Critic 方法：用单独的 actor 网络输出动作， critic 网络评估。这是 DDPG 、 TD3 、 SAC 的思路（下一章介绍） - NAF（ Normalized Advantage Functions）：将 Q 函数参数化为二次型，最优动作解析解为总结： DQN 是为离散动作设计的，扩展到连续动作需要额外的架构创新。

Q7：如何判断 DQN 训练是否收敛？

A：判断收敛的多个指标：

Reward 稳定：在测试环境中（ deterministic，无探索），连续 100 个 episode 的平均 reward 不再增长，且方差小于 5%。
Q 值稳定：监控的变化率：

如果连续 1000 步的，说明 Q 值已收敛。

策略稳定：在相同状态下，连续多次推理的动作一致性： $相同动作总次数$ 4. TD 误差稳定：测试集上的平均 TD 误差降到接近 0 。

实践中， Atari 游戏通常需要 10M-50M 帧（约 200-1000 episodes）才能收敛。如果训练 1000 episodes 后 reward 仍在随机游走，说明有问题。

Q8： DQN vs PPO，什么时候用哪个？

A： DQN 和 PPO 各有适用场景：

特性	DQN	PPO
动作空间	离散（小规模）	离散+连续
样本效率	高（经验回放）	低（ on-policy）
稳定性	需调参（目标网络等）	开箱即用
并行化	单环境训练	多环境并行
适用任务	Atari 、离散控制	机器人、连续控制

选择建议： - 离散动作 + 样本昂贵（如机器人抓取每次尝试 5 分钟） → DQN - 连续动作 + 可大量采样（如模拟器环境） → PPO - 需要快速原型（不想调参） → PPO - 追求极致性能（愿意精调） → Rainbow DQN

有趣的现象：在 Atari 上， DQN 的最终性能通常高于 PPO，但 PPO 的训练曲线更平滑。这反映了 off-policy 方法的"高风险高回报"特性。

Q9：如何处理高维图像输入（ Atari）？

A： Atari 环境的原始观测是 210x160x3 的 RGB 图像，直接作为输入会导致：

维度过高： 210x160x3 = 100,800 维，网络参数量爆炸
冗余信息：大部分像素是背景（黑色），信息密度低
时间相关性：单帧无法判断速度（如球的运动方向）

DQN 的预处理流程：

步骤 1：灰度化

1	gray = np.dot(rgb[...,:3], [0.299, 0.587, 0.114]) # 转灰度

步骤 2：裁剪无关区域

1	cropped = gray[34:194, :] # 去掉 Pong 的顶部得分栏

步骤 3：下采样

1	resized = cv2.resize(cropped, (84, 84)) # 缩放到 84x84

步骤 4：帧栈（ Frame Stacking）

1	state = np.stack([frame_t, frame_{t-1}, frame_{t-2}, frame_{t-3}], axis=0) # 4 帧栈

帧栈解决了速度信息问题——网络可以通过比较相邻帧推断运动方向。

步骤 5：归一化

1	state = state / 255.0 # 归一化到[0, 1]

经过这些处理，输入从 100,800 维降到 84x84x4 = 28,224 维，信息密度大幅提升。

Q10： DQN 的 sample efficiency 如何？

A： Sample efficiency 衡量的是"达到目标性能需要多少样本"。 DQN 在这方面表现中等：

与表格方法比较： - 表格 Q-Learning（ CartPole）：约 5000 步 - DQN（ CartPole）：约 50,000 步

DQN 需要 10 倍样本，因为神经网络需要更多数据来拟合 Q 函数。

与 on-policy 方法比较： - DQN（ Atari Pong）：约 200 万帧 - A3C（ on-policy）：约 1000 万帧

DQN 的经验回放提升了 5 倍样本效率。

与 model-based 方法比较： - DQN（模拟器环境）：约 10 万步 - Dyna-Q（ model-based）：约 1 万步

Model-based 方法通过学习环境模型并在模型中模拟，可以用更少的真实交互。

绝对数值：在 Atari 上， DQN 通常需要 10M-50M 帧（约 40-200 小时游戏时间）才能达到人类水平。这对于机器人等真实环境来说是不可接受的——因此实际应用中， DQN 更多用于模拟器环境，或结合 sim-to-real 技术。

提升 sample efficiency 的方向： - 更好的网络架构（如 ResNet 、 Transformer） - 辅助任务（如自监督学习、对比学习） - 迁移学习（预训练+微调）

参考文献

以下是 DQN 及其变体的核心论文（按时间顺序）：

Watkins, C. J., & Dayan, P. (1992). Q-learning. Machine Learning, 8(3-4), 279-292.
论文链接
Q-Learning 算法的收敛性证明
Mnih, V., Kavukcuoglu, K., Silver, D., et al. (2013). Playing Atari with Deep Reinforcement Learning. NIPS Deep Learning Workshop.
arXiv:1312.5602
DQN 首次提出，引入经验回放和目标网络
Mnih, V., Kavukcuoglu, K., Silver, D., et al. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529-533.
Nature 论文
DQN 完整版，在 49 款 Atari 游戏上达到人类水平
van Hasselt, H., Guez, A., & Silver, D. (2016). Deep Reinforcement Learning with Double Q-learning. AAAI.
arXiv:1509.06461
Double DQN，解决 Q 值过估计
Wang, Z., Schaul, T., Hessel, M., et al. (2016). Dueling Network Architectures for Deep Reinforcement Learning. ICML.
arXiv:1511.06581
Dueling DQN，分离状态价值与优势函数
Schaul, T., Quan, J., Antonoglou, I., & Silver, D. (2016). Prioritized Experience Replay. ICLR.
arXiv:1511.05952
PER，根据 TD 误差优先采样
Fortunato, M., Azar, M. G., Piot, B., et al. (2018). Noisy Networks for Exploration. ICLR.
arXiv:1706.10295
Noisy Networks，可学习的探索噪声
Bellemare, M. G., Dabney, W., & Munos, R. (2017). A Distributional Perspective on Reinforcement Learning. ICML.
arXiv:1707.06887
C51，学习值分布而非期望
Hessel, M., Modayil, J., van Hasselt, H., et al. (2018). Rainbow: Combining Improvements in Deep Reinforcement Learning. AAAI.
arXiv:1710.02298
Rainbow，集成 6 种 DQN 改进技术
Sutton, R. S., & Barto, A. G. (2018). Reinforcement Learning: An Introduction (2nd ed.). MIT Press.
在线版
强化学习经典教材，详细讲解 Q-Learning 和 Deadly Triad

从 Q-Learning 的表格更新到 DQN 的深度学习，从单一算法到 Rainbow 的技术集成， value-based 方法在过去三十年经历了巨大演进。 DQN 的两大创新——经验回放和目标网络——不仅解决了深度 Q 网络的稳定性问题，也为后续的 Deep RL 算法提供了设计范式。 Double DQN 、 Dueling DQN 、 PER 等变体各有侧重，针对性地解决过估计、学习效率、样本效率等问题。 Rainbow 的成功表明，精心组合的技术栈能产生超过简单叠加的协同效应。

然而， DQN 的局限也很明显：仅适用于离散动作空间，在连续控制任务中捉襟见肘。下一章我们将转向 Policy Gradient 方法和 Actor-Critic 架构，探讨如何直接优化策略，并自然地处理连续动作空间——这将引领我们进入 DDPG 、 TD3 、 SAC 等现代算法的世界。