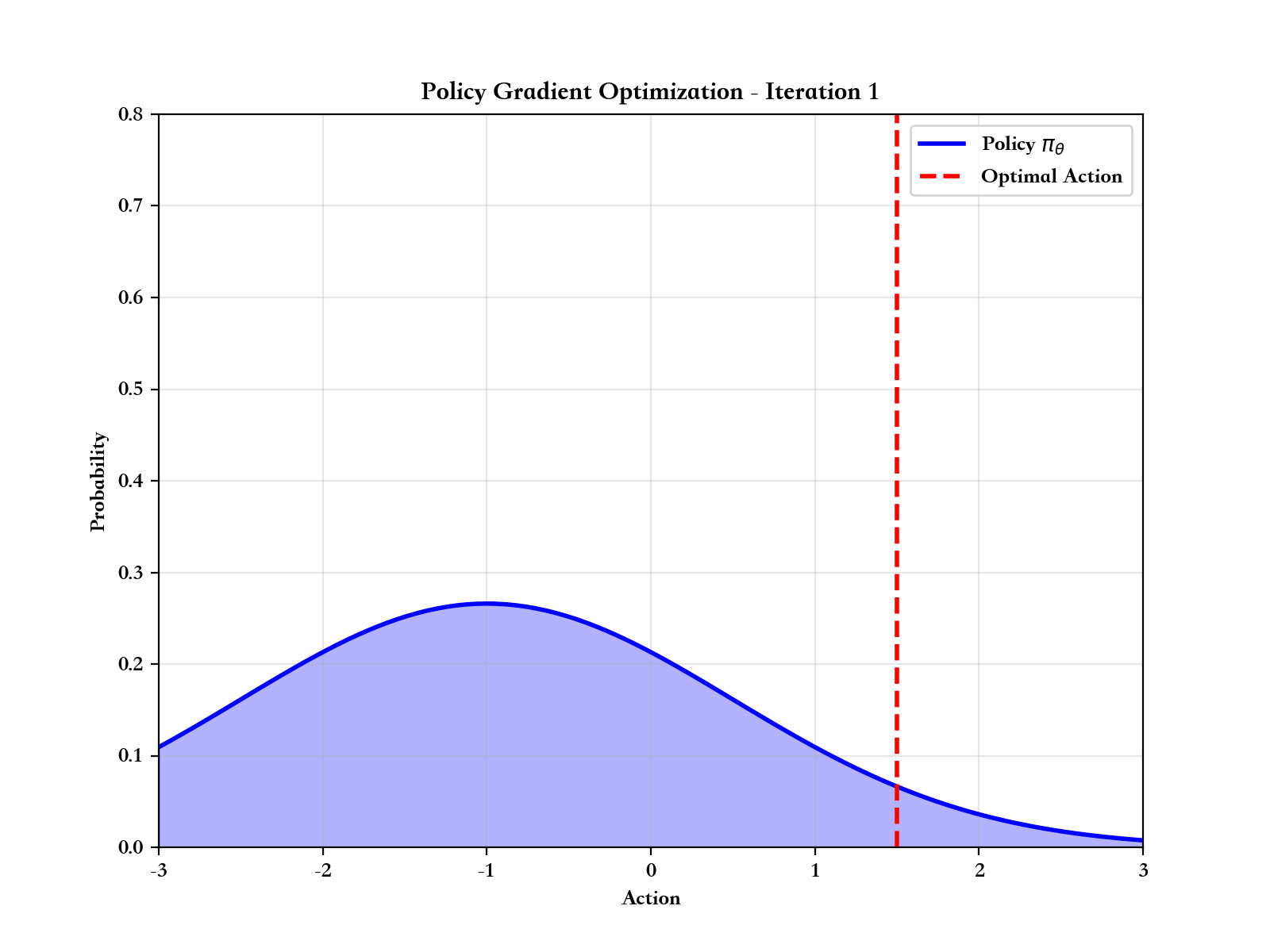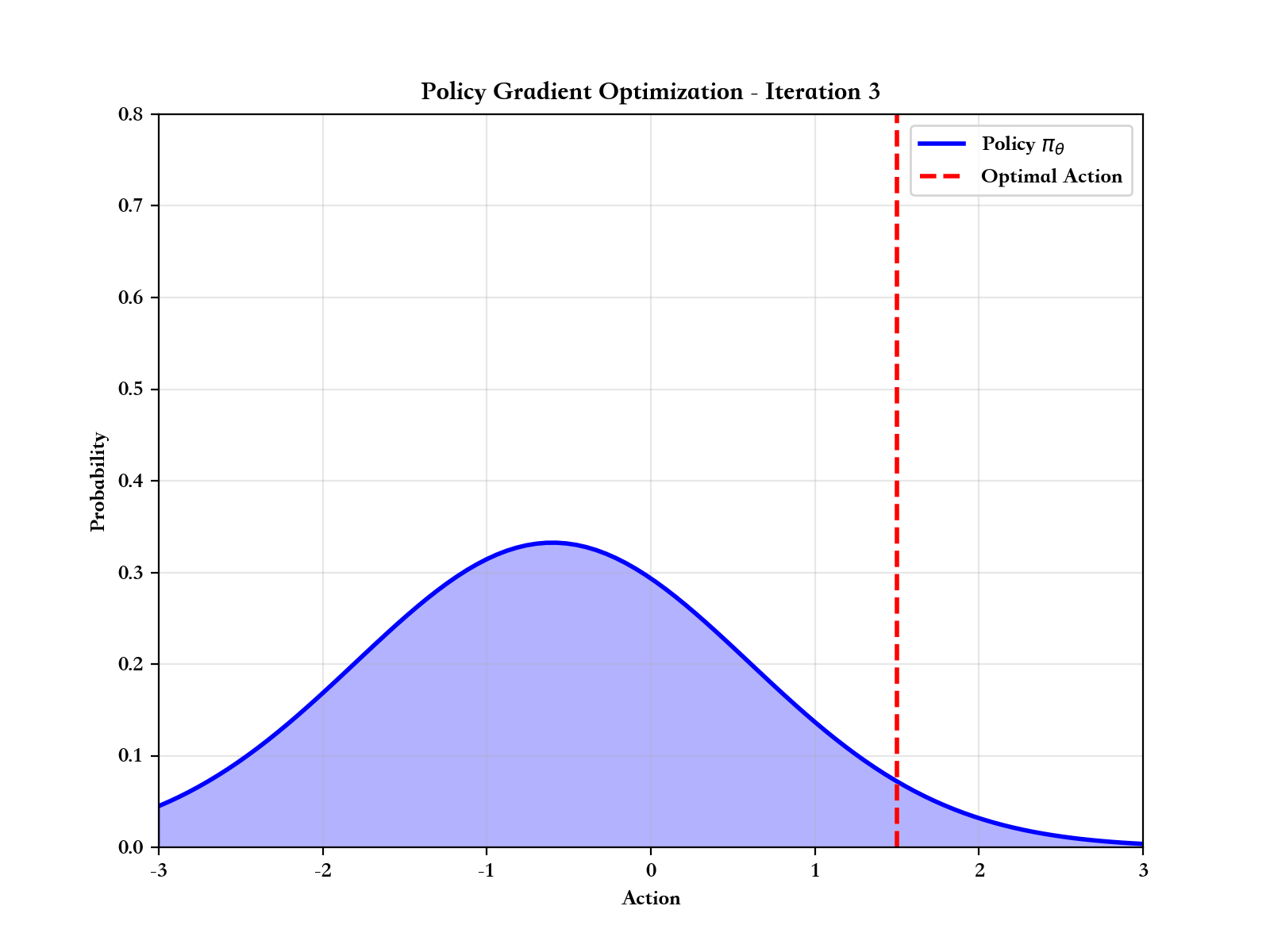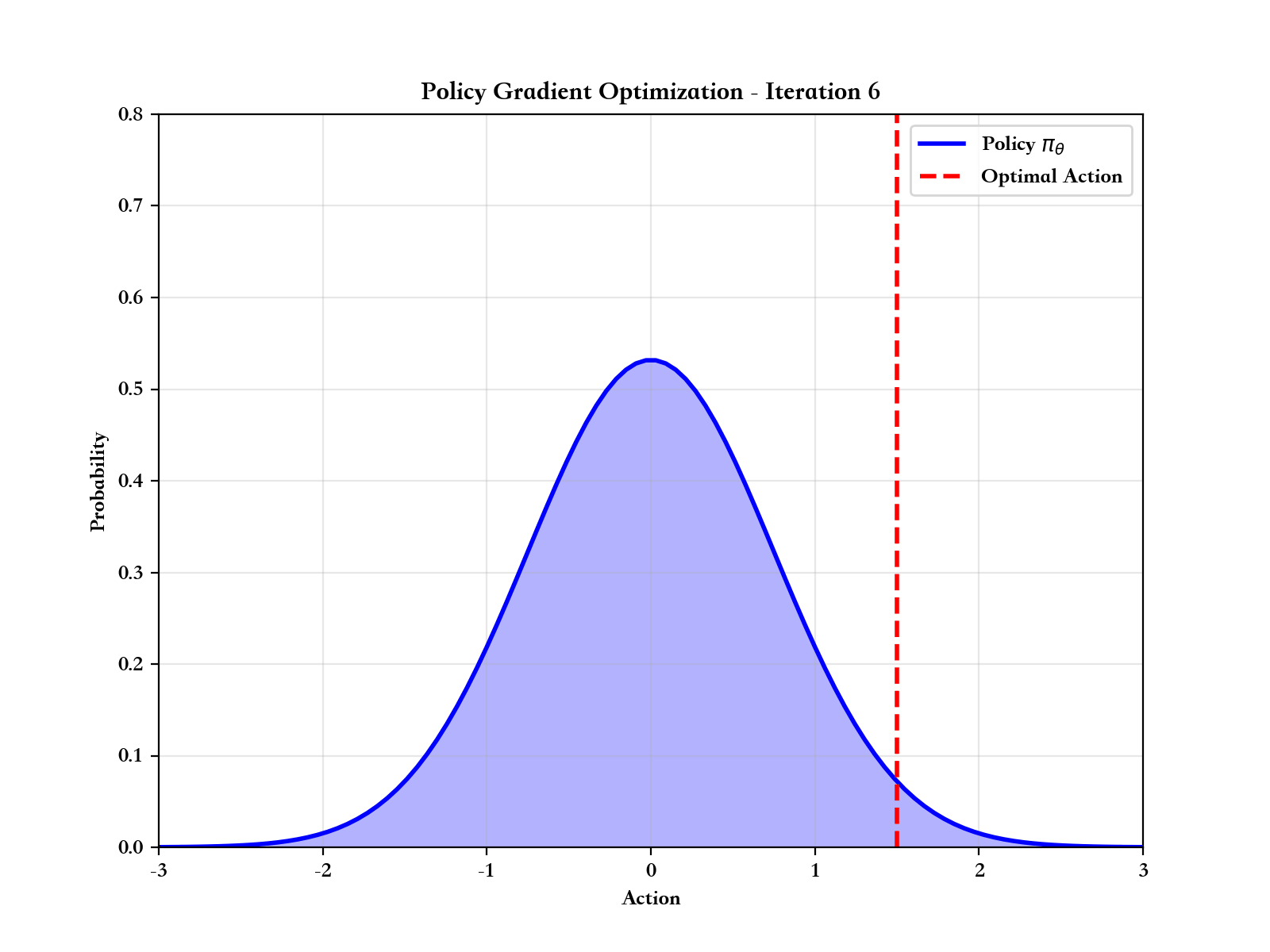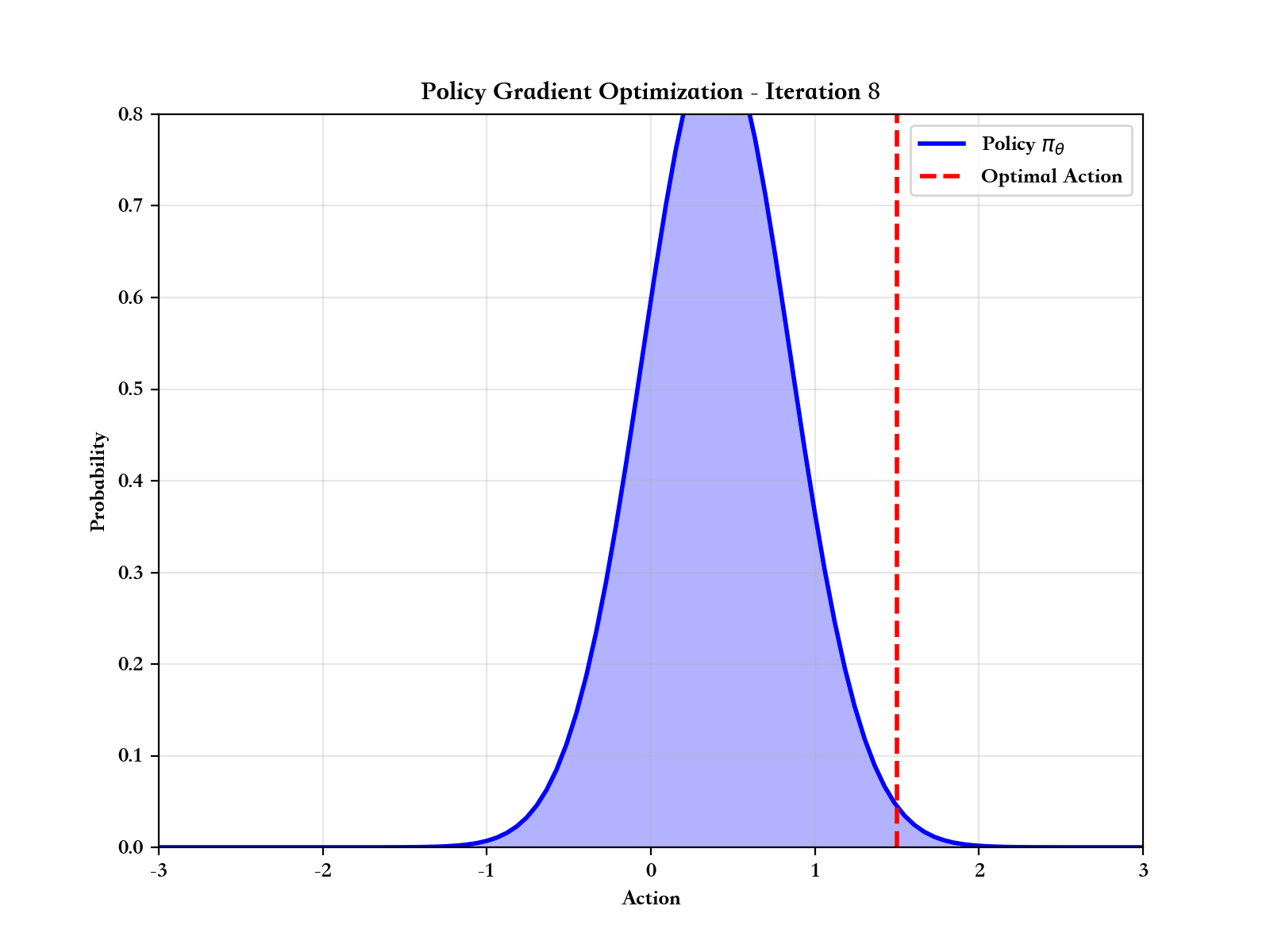
强化学习（三）—— Policy Gradient 与 Actor-Critic 方法

如果说价值函数方法是通过"评估动作好坏"来间接学习策略，那么策略梯度方法则是直接优化策略本身。 DQN 的成功证明了深度学习在强化学习中的巨大潜力,但其局限也很明显——只能处理离散动作空间,在机器人控制、自动驾驶等连续控制任务中无能为力。 Policy Gradient 方法通过将策略参数化为神经网络,利用梯度上升直接最大化期望回报,天然支持连续动作。从最早的 REINFORCE 算法到结合价值函数的 Actor-Critic 架构,从异步并行的 A3C 到突破性的 DDPG,从样本高效的 TD3 到工业界广泛应用的 PPO,再到最大熵框架下的 SAC ——策略梯度方法已经发展成深度强化学习的主流技术路线。本章将系统梳理这一演进路径,深入剖析每个算法的设计动机、数学原理和实现细节。

Policy Gradient 基础：直接优化策略

为什么需要 Policy Gradient

在第二章中,我们看到 DQN 通过学习 Q 函数并贪心选择动作来获得策略。这种间接方式有几个问题:

问题 1：只能处理离散动作

DQN 需要计算,在离散空间(如 Atari 的 18 个动作)可以遍历,但在连续空间(如机器人关节角度)需要求解优化问题,计算昂贵且不精确。

问题 2：确定性策略的探索困境

贪心策略是完全确定的,探索只能依赖-greedy 等启发式方法,缺乏原则性指导。

问题 3：值函数近似误差的累积

在高维状态空间,Q 函数的逼近误差会通过操作累积并放大(如第二章的过估计问题),影响最终策略质量。

问题 4：无法表示随机策略

某些问题的最优策略本身就是随机的。经典例子是石头剪刀布游戏——确定性策略必然被对手利用,最优策略是等概率随机。

Policy Gradient 方法通过直接参数化策略来规避这些问题: - 策略可以输出动作的概率分布(离散)或分布参数(连续),天然支持随机策略 - 对于连续动作,通常用高斯分布,直接输出均值和方差 - 优化目标是期望回报,通过梯度上升直接优化

策略梯度定理

设策略由参数控制,目标是最大化期望回报:

J() = {} = {s d^} [V^{_}(s)] $$

其中是策略诱导的状态分布, 是轨迹。

直觉上,我们想对求梯度:。但问题是期望里面的依赖于(策略变了,轨迹分布就变了),不能简单交换梯度和期望。

策略梯度定理(Policy Gradient Theorem, Sutton et al., 2000)给出了精确的梯度表达式:

这个公式非常优美: - 是 score function(得分函数),衡量参数变化对选择概率的影响 - 是该动作的长期价值 - 两者相乘:价值高的动作,增大其概率;价值低的动作,减小其概率

更妙的是,梯度不依赖于状态转移概率——即使环境模型未知,只要能采样轨迹,就能估计梯度。

推导:从轨迹分布到策略梯度

完整推导需要一些技巧。首先,将目标写成轨迹分布:

J() = P_() R() d $$

其中是轨迹概率。

对求导:

使用 log-derivative 技巧:,得到:

展开:

对求导时, 和不依赖,消失:

代入得:

这是 REINFORCE 算法的形式。进一步,注意到时刻的动作只影响之后的奖励(因果性),可以替换为,得到:

其中正是的无偏估计。这就是策略梯度定理。

Baseline：减小方差

策略梯度的一个问题是方差很大。考虑可能从-100 到+100,导致梯度估计非常不稳定。

一个简单但有效的技巧是减去一个 baseline:

只要不依赖,梯度的期望不变(因为),但方差可以大幅降低。

最常用的 baseline 是状态价值函数,此时:

A_t = G_t - V(s_t) $$

称为优势函数(advantage function)。直觉上, 是该状态的"平均"价值, 衡量动作比平均水平好多少。用替代,只强化"好于平均"的动作,避免所有动作概率都增大(即使有些动作很差)。

REINFORCE 算法：蒙特卡洛策略梯度

算法流程

REINFORCE(Williams, 1992)是最简单的策略梯度算法:

算法:REINFORCE

随机初始化策略参数$= 1, 2, , M$do
生成一条轨迹遵循 $Missing superscript or subscript argument_$ 4. for do
计算回报$G_t = {t'=t}^{T-1} ^{t'-t} r{t'}$6. 累积梯度$J = _(a_t|s_t) G_t$7. end for
更新参数9. end for

关键点: - 第 3 行:采样完整轨迹(on-policy,必须用当前策略) - 第 5 行:从到终止的折扣回报(蒙特卡洛估计) - 第 6 行:策略梯度公式 - 第 8 行:梯度上升更新

带 Baseline 的 REINFORCE

加入状态价值函数作为 baseline:

算法:REINFORCE with Baseline

初始化策略参数和价值函数参数$= 1, 2, $do
生成轨迹遵循 $Missing superscript or subscript argument_$ 4. for do
$

G_t {t'=t}^{T-1} ^{t'-t} r{t'}$6. $

A_t G_t - V_(s_t)$(优势估计) 7. 策略梯度$J = (a_t|s_t) A_t$8. 价值函数损失$V = (G_t - V(s_t))^2$9. end for 10. 更新$+ J$11. 更新$- __V$12. end for

第 8 行用均方误差训练价值函数,使其逼近真实回报。

代码实现:CartPole

下面用 PyTorch 实现 REINFORCE 解决 CartPole 环境:

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import gym
import numpy as np

class PolicyNetwork(nn.Module):
    """策略网络:输出动作概率分布"""
    def __init__(self, state_dim, action_dim, hidden_dim=128):
        super(PolicyNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, action_dim)
    
    def forward(self, state):
        x = F.relu(self.fc1(state))
        x = F.relu(self.fc2(x))
        action_logits = self.fc3(x)
        return F.softmax(action_logits, dim=-1)

class ValueNetwork(nn.Module):
    """价值网络:输出状态价值"""
    def __init__(self, state_dim, hidden_dim=128):
        super(ValueNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, 1)
    
    def forward(self, state):
        x = F.relu(self.fc1(state))
        x = F.relu(self.fc2(x))
        return self.fc3(x)

def compute_returns(rewards, gamma=0.99):
    """计算折扣回报"""
    returns = []
    R = 0
    for r in reversed(rewards):
        R = r + gamma * R
        returns.insert(0, R)
    return returns

def reinforce_with_baseline(env_name='CartPole-v1', episodes=1000, gamma=0.99):
    env = gym.make(env_name)
    state_dim = env.observation_space.shape[0]
    action_dim = env.action_space.n
    
    # 初始化网络
    policy_net = PolicyNetwork(state_dim, action_dim)
    value_net = ValueNetwork(state_dim)
    
    policy_optimizer = optim.Adam(policy_net.parameters(), lr=3e-4)
    value_optimizer = optim.Adam(value_net.parameters(), lr=1e-3)
    
    episode_rewards = []
    
    for episode in range(episodes):
        state = env.reset()
        log_probs = []
        values = []
        rewards = []
        
        # 采样轨迹
        while True:
            state_tensor = torch.FloatTensor(state).unsqueeze(0)
            
            # 策略网络选择动作
            action_probs = policy_net(state_tensor)
            dist = Categorical(action_probs)
            action = dist.sample()
            
            # 价值网络估计状态价值
            value = value_net(state_tensor)
            
            # 执行动作
            next_state, reward, done, _ = env.step(action.item())
            
            # 记录
            log_probs.append(dist.log_prob(action))
            values.append(value)
            rewards.append(reward)
            
            state = next_state
            
            if done:
                break
        
        # 计算回报
        returns = compute_returns(rewards, gamma)
        returns = torch.FloatTensor(returns)
        
        # 转换为 tensor
        log_probs = torch.stack(log_probs)
        values = torch.cat(values)
        
        # 计算优势
        advantages = returns - values.detach()
        
        # 策略损失(负号因为要做梯度上升)
        policy_loss = -(log_probs * advantages).mean()
        
        # 价值损失
        value_loss = F.mse_loss(values, returns)
        
        # 更新
        policy_optimizer.zero_grad()
        policy_loss.backward()
        policy_optimizer.step()
        
        value_optimizer.zero_grad()
        value_loss.backward()
        value_optimizer.step()
        
        episode_rewards.append(sum(rewards))
        
        if (episode + 1) % 100 == 0:
            avg_reward = np.mean(episode_rewards[-100:])
            print(f"Episode {episode+1}, Avg Reward: {avg_reward:.2f}")
    
    return policy_net, value_net, episode_rewards

# 运行训练
policy_net, value_net, rewards = reinforce_with_baseline(episodes=1000)

# 可视化
import matplotlib.pyplot as plt

plt.figure(figsize=(10, 5))
plt.plot(rewards, alpha=0.3)
plt.plot(np.convolve(rewards, np.ones(50)/50, mode='valid'), linewidth=2)
plt.xlabel('Episode')
plt.ylabel('Total Reward')
plt.title('REINFORCE with Baseline on CartPole')
plt.grid(True)
plt.show()

这段代码通常在 100-200 个 episode 内就能解决 CartPole(平均奖励>195)。

REINFORCE 的优缺点

优点: - 简单直观,易于实现 - 无偏梯度估计(因为用真实回报) - 天然支持连续动作空间(只需改变策略网络输出分布)

缺点: - 高方差: 的随机性很大,即使有 baseline - 样本效率低:on-policy,每条轨迹只用一次 - 训练不稳定:学习曲线震荡严重

这些缺点促使研究者探索更先进的方法。

Actor-Critic 架构:结合策略与价值

从 REINFORCE 到 Actor-Critic

REINFORCE 用完整回报估计 Q 值,这是蒙特卡洛方法,方差大。能否用时序差分(TD)来降低方差?

回顾策略梯度:

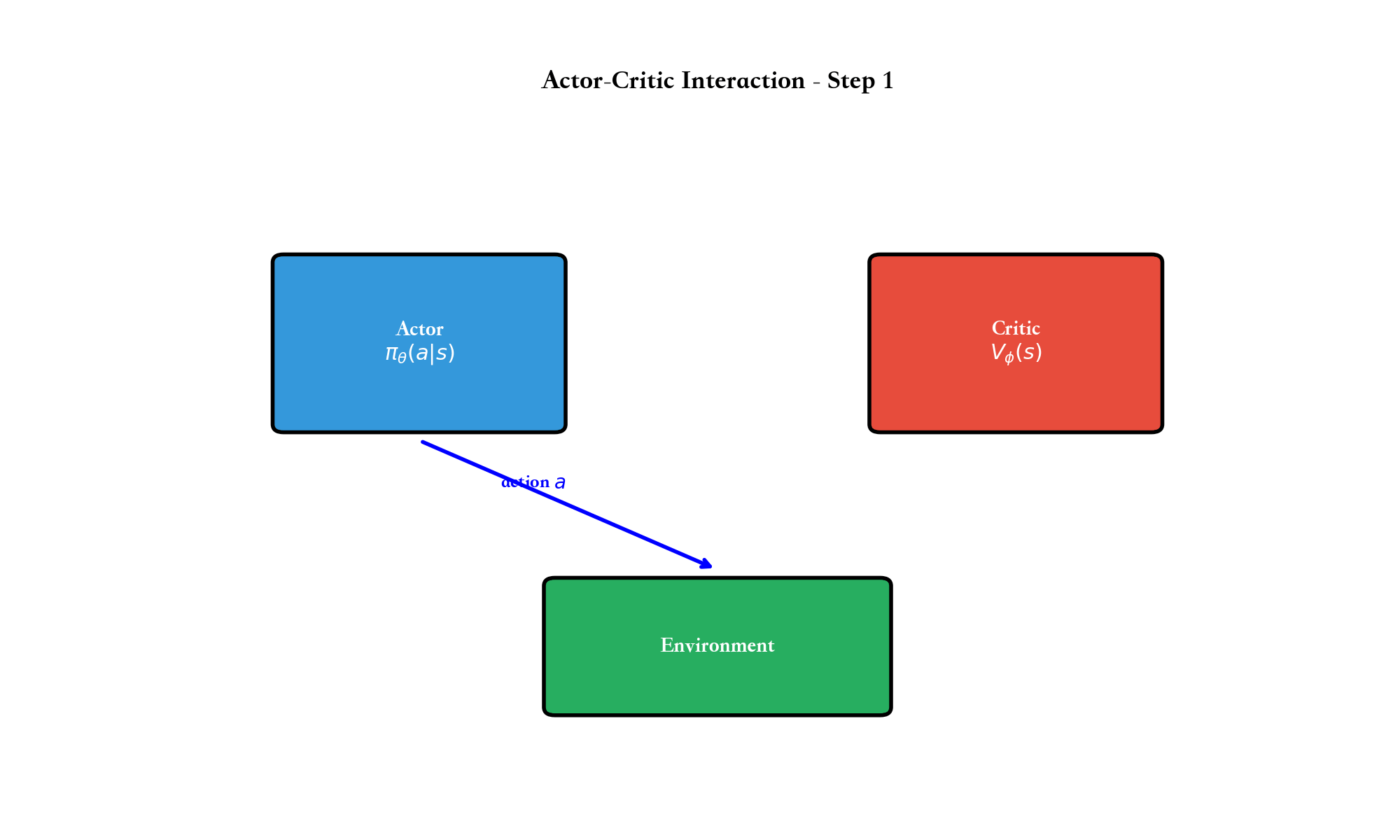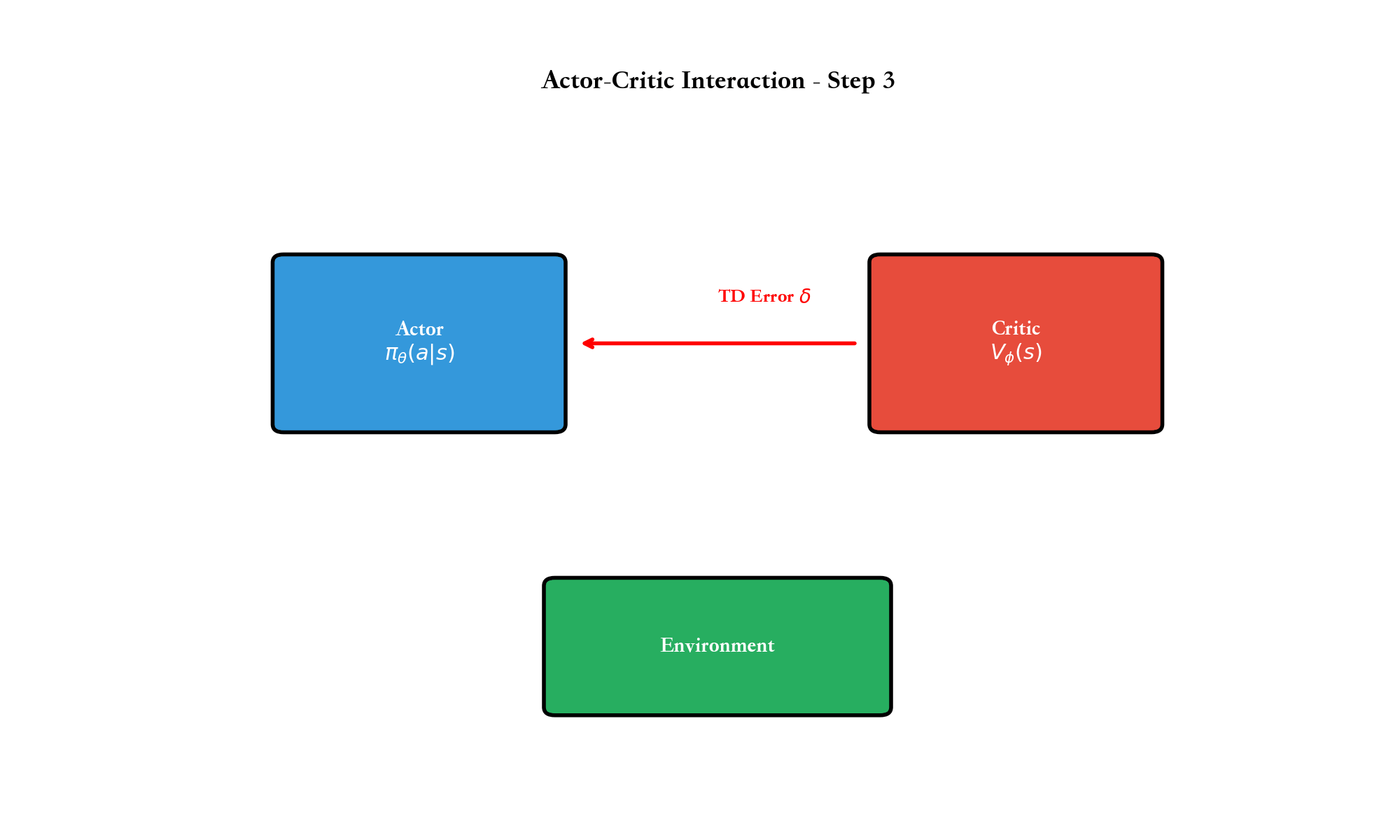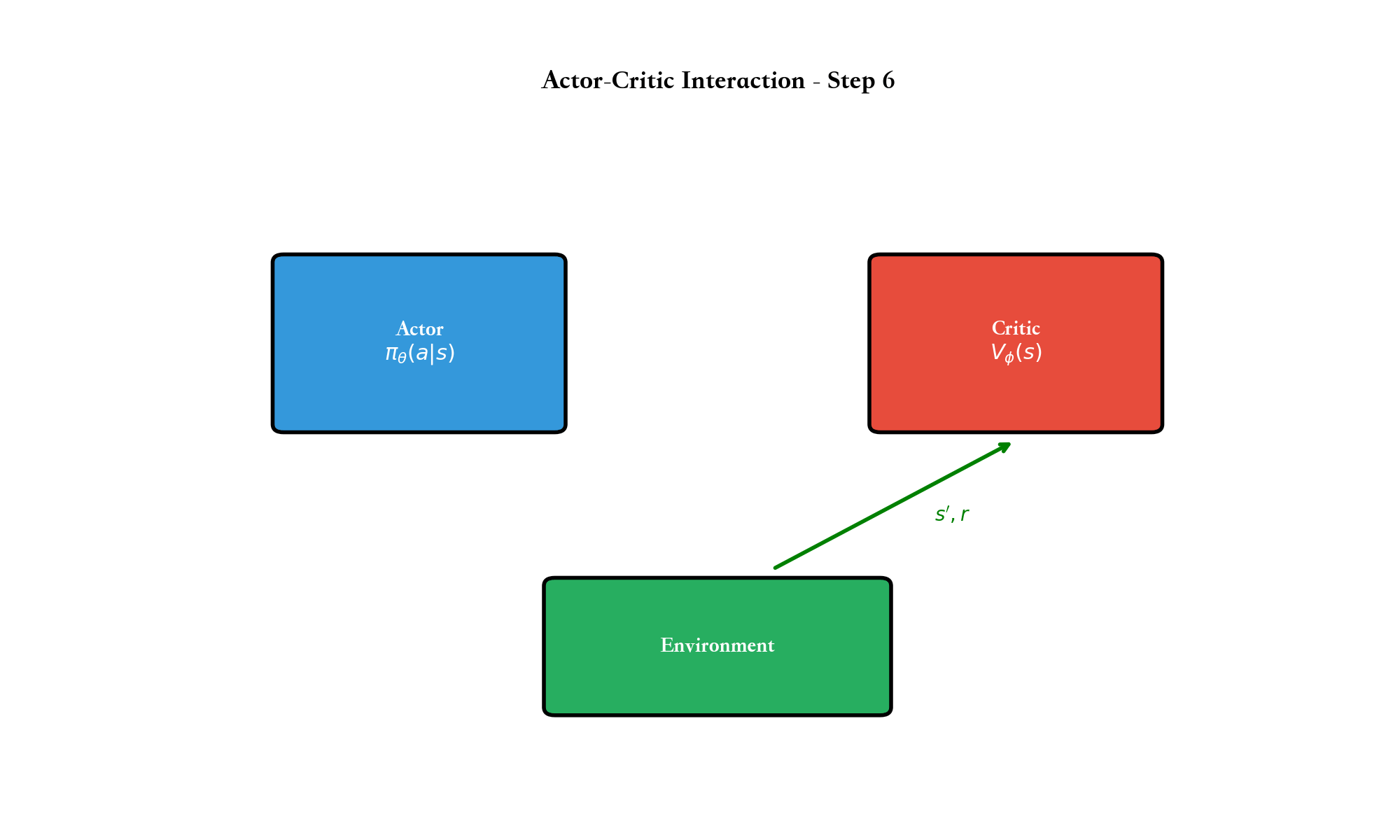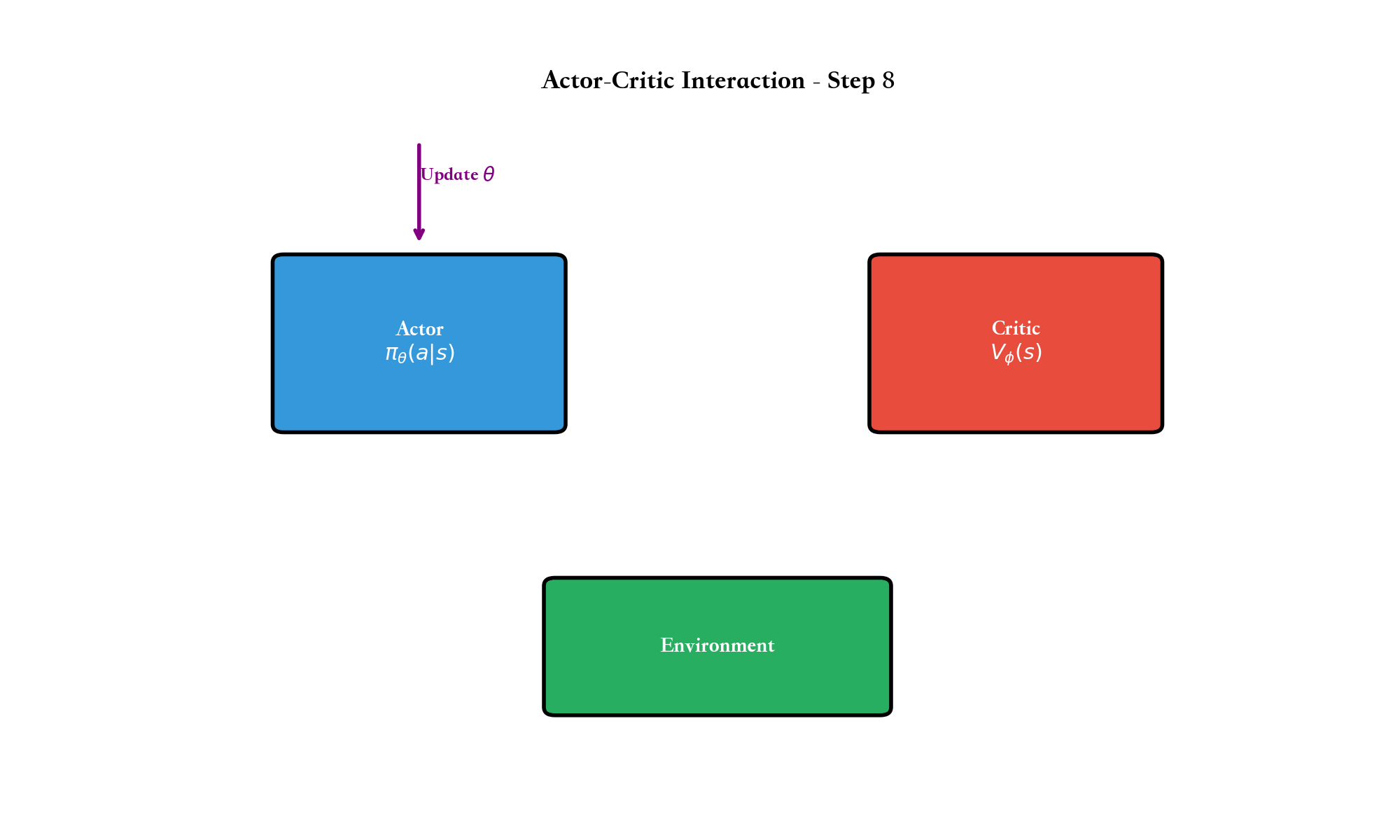
在 REINFORCE 中, 用估计。 Actor-Critic 的想法是:用一个神经网络或来近似 Q 值,然后用 TD 方法训练这个网络。

架构分为两部分: - Actor(演员):策略网络,负责选择动作 - Critic(评论家):价值网络或,负责评估动作

Actor 根据 Critic 的反馈更新,Critic 根据环境的奖励更新。这种"演员-评论家"的互动是 Actor-Critic 名字的由来。

优势 Actor-Critic(A2C)

使用状态价值函数作为 Critic,优势函数估计为:

A_t = r_t + V_(s_{t+1}) - V_(s_t) $$

这是 1-step TD 误差。相比,它的方差更小(只依赖一步转移),但引入了偏差(因为是近似的)。

完整算法:

算法:Advantage Actor-Critic (A2C)

初始化 Actor 参数和 Critic 参数$= 1, 2, $do
观察状态4. 根据选择动作$a_t (|s_t)$5. 执行,观察$r_t, s{t+1}$6. 计算 TD 误差$t = r_t + V(s_{t+1}) - V_(s_t)$7. 更新 Critic:$- t^2$8. 更新 Actor:$+ (a_t|s_t) _t$9. end for

注意: - 第 6 行用 TD 误差作为优势估计 - 第 7 行最小化价值函数的 TD 误差 - 第 8 行用 TD 误差指导策略更新

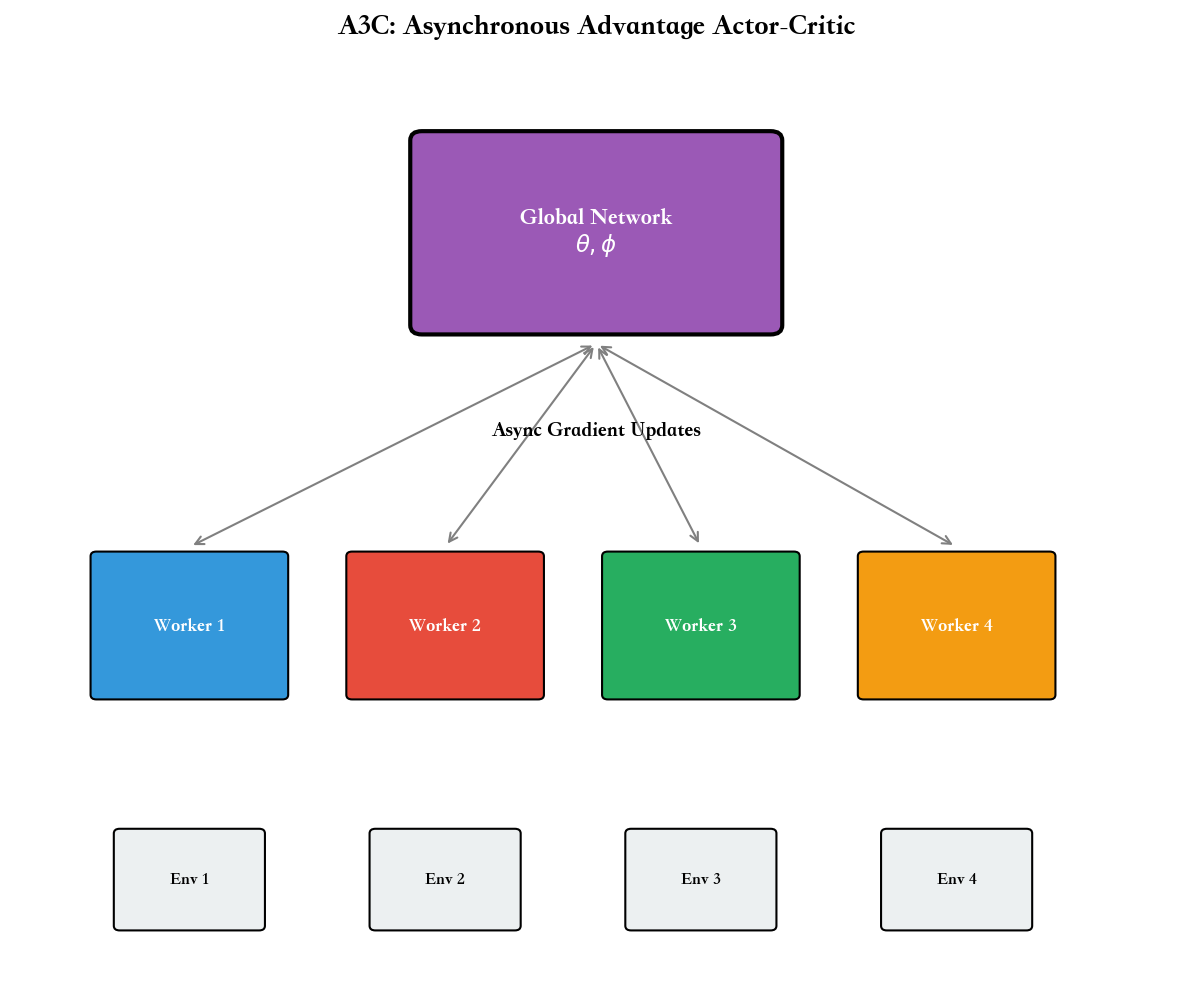
A3C:异步优势 Actor-Critic

A3C(Asynchronous Advantage Actor-Critic, Mnih et al., 2016)是 A2C 的并行版本,也是第一个在 Atari 上与 DQN 竞争的 on-policy 算法。

核心思想:并行运行多个环境实例,每个 worker 独立采样并计算梯度,异步更新共享的全局参数。

为什么并行有效? - 打破样本相关性:不同 worker 的经验来自不同状态,相关性降低 - 加速训练:多核 CPU 可以同时采样,GPU 用于更新网络 - 探索多样性:不同 worker 可以使用不同的探索策略(如不同的)

伪代码(简化版):

算法:A3C(单个 Worker)

全局参数共享
Worker:
初始化局部参数4. loop
同步6. 采样步经验$(s_t, a_t, r_t){t=1}^n$7. 计算 n-step return:$R_t = {k=0}^{n-1} ^k r_{t+k} + ^n V_{'}(s_{t+n})$8. 计算优势9. 累积策略梯度$J = t {'} {'}(a_t|s_t) A_t$10. 累积价值梯度$_V = t {'} (R_t - V{'}(s_t))^2$11. 异步更新全局参数12. end loop

A3C 在 2016 年取得了巨大成功,在 Atari 上达到接近 DQN 的性能,且训练速度更快(利用了多核 CPU)。但它也有缺点:异步更新可能导致梯度过时(一个 worker 计算梯度时,全局参数已被其他 worker 修改),影响稳定性。

现代实现通常使用同步版本 A2C(去掉"Asynchronous"),在多个环境中并行采样,统一更新参数,避免异步带来的问题。

代码实现:A2C 多环境

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import gym
import numpy as np

class ActorCritic(nn.Module):
    """共享参数的 Actor-Critic 网络"""
    def __init__(self, state_dim, action_dim, hidden_dim=128):
        super(ActorCritic, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        
        # Actor 头
        self.actor = nn.Linear(hidden_dim, action_dim)
        
        # Critic 头
        self.critic = nn.Linear(hidden_dim, 1)
    
    def forward(self, state):
        x = F.relu(self.fc1(state))
        x = F.relu(self.fc2(x))
        
        action_probs = F.softmax(self.actor(x), dim=-1)
        state_value = self.critic(x)
        
        return action_probs, state_value

def a2c_multi_env(env_name='CartPole-v1', n_envs=8, n_steps=5, 
                  episodes=500, gamma=0.99):
    # 创建多个环境
    envs = [gym.make(env_name) for _ in range(n_envs)]
    state_dim = envs[0].observation_space.shape[0]
    action_dim = envs[0].action_space.n
    
    # 初始化网络
    model = ActorCritic(state_dim, action_dim)
    optimizer = optim.Adam(model.parameters(), lr=3e-4)
    
    # 初始化状态
    states = [env.reset() for env in envs]
    episode_rewards = [0] * n_envs
    all_rewards = []
    
    for step in range(episodes * 200 // n_envs):  # 总步数
        # 存储 n 步经验
        log_probs_list = []
        values_list = []
        rewards_list = []
        dones_list = []
        
        for _ in range(n_steps):
            states_tensor = torch.FloatTensor(states)
            
            # 前向传播
            action_probs, values = model(states_tensor)
            dist = Categorical(action_probs)
            actions = dist.sample()
            
            log_probs_list.append(dist.log_prob(actions))
            values_list.append(values.squeeze())
            
            # 执行动作
            next_states = []
            rewards = []
            dones = []
            
            for i, (env, action) in enumerate(zip(envs, actions)):
                next_state, reward, done, _ = env.step(action.item())
                
                episode_rewards[i] += reward
                rewards.append(reward)
                dones.append(done)
                
                if done:
                    all_rewards.append(episode_rewards[i])
                    episode_rewards[i] = 0
                    next_state = env.reset()
                
                next_states.append(next_state)
            
            rewards_list.append(torch.FloatTensor(rewards))
            dones_list.append(torch.FloatTensor(dones))
            states = next_states
        
        # 计算 n-step return
        with torch.no_grad():
            next_states_tensor = torch.FloatTensor(states)
            _, next_values = model(next_states_tensor)
            next_values = next_values.squeeze()
        
        returns = next_values
        advantage_list = []
        
        for t in reversed(range(n_steps)):
            returns = rewards_list[t] + gamma * returns * (1 - dones_list[t])
            advantage = returns - values_list[t]
            advantage_list.insert(0, advantage)
        
        # 计算损失
        log_probs = torch.stack(log_probs_list)
        values = torch.stack(values_list)
        advantages = torch.stack(advantage_list)
        returns_all = values + advantages
        
        actor_loss = -(log_probs * advantages.detach()).mean()
        critic_loss = F.mse_loss(values, returns_all.detach())
        
        # 熵正则化(鼓励探索)
        entropy = -(action_probs * torch.log(action_probs + 1e-8)).sum(dim=-1).mean()
        
        loss = actor_loss + 0.5 * critic_loss - 0.01 * entropy
        
        # 更新
        optimizer.zero_grad()
        loss.backward()
        torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=0.5)
        optimizer.step()
        
        if (step + 1) % 100 == 0 and len(all_rewards) > 0:
            print(f"Step {step+1}, Avg Reward: {np.mean(all_rewards[-100:]):.2f}")
    
    return model, all_rewards

# 运行
model, rewards = a2c_multi_env(n_envs=8, episodes=500)

这个实现使用 8 个并行环境,每次采样 5 步(n-step return),大幅提升样本效率和训练速度。

连续控制:DDPG 与 TD3

从离散到连续:挑战

前面的算法(REINFORCE, A2C)都针对离散动作空间。对于连续动作(如机器人关节角度、自动驾驶的方向盘角度),策略通常建模为高斯分布:

网络输出均值和标准差,采样动作。

但这种随机策略有个问题:在某些任务中(如精确控制),最优策略可能是确定性的。每次都采样引入不必要的噪声,降低性能。

DDPG(Deep Deterministic Policy Gradient)的思路是:学习一个确定性策略,直接输出动作,不需要采样。

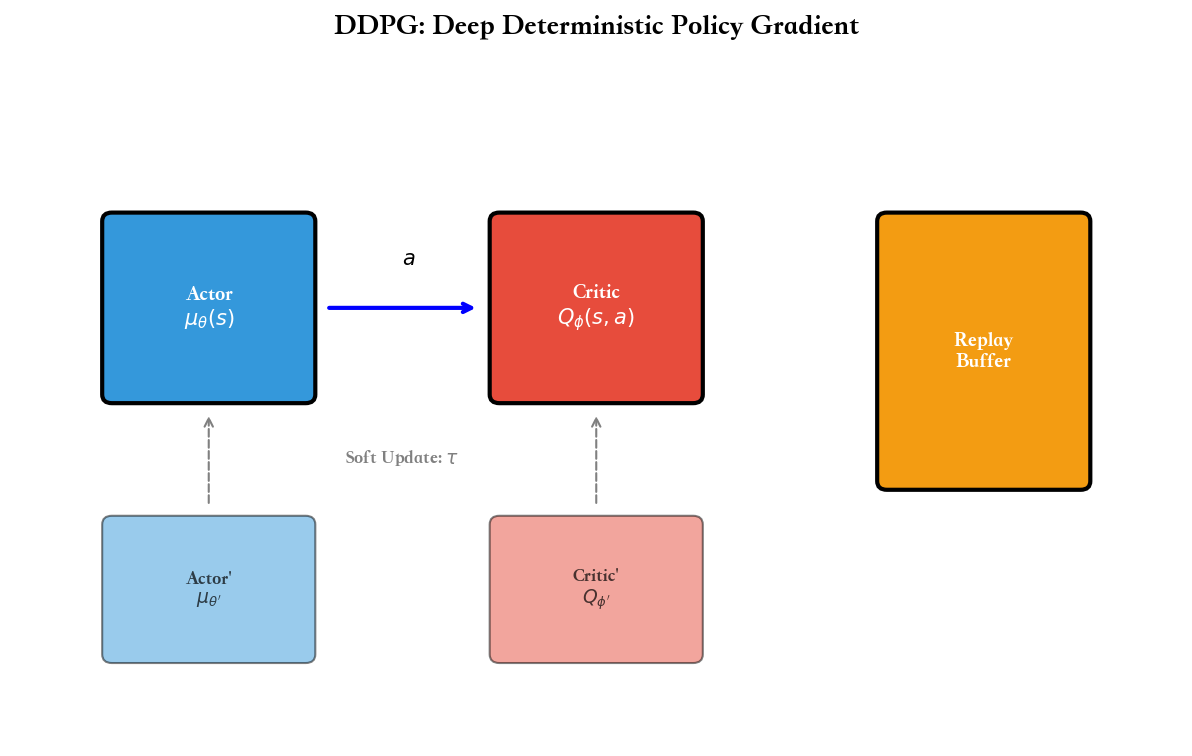
DDPG:确定性策略梯度

DDPG(Lillicrap et al., 2016)结合了 DQN 和 Actor-Critic 的思想: - 像 DQN 一样使用经验回放和目标网络 - 像 Actor-Critic 一样分离策略(Actor)和价值(Critic)

确定性策略梯度定理(Silver et al., 2014)指出,对于确定性策略,梯度为:

直觉:价值函数告诉我们"在状态下,动作有多好",我们想让策略输出的动作沿着使增大的方向移动。是 Q 关于动作的梯度,指向 Q 值增大的方向; 是策略关于参数的梯度,链式法则连接两者。

DDPG 算法:

算法:DDPG

初始化 Actor, Critic$Q_ $初始化目标网络$ _{'}$, : $' , ' $初始化经验回放$ = 1, 2, $do
初始化随机探索噪声$$6. 重置环境,得到初始状态7. for do
选择动作(加噪声探索)
执行,观察10. 存储到$$11. 从中采样小批量$(s_i, a_i, r_i, s'i)$12. 计算目标$y_i = r_i + Q{'}(s'i, {'}(s'i))$13. 更新 Critic:最小化$ = i (y_i - Q(s_i, a_i))^2$14. 更新 Actor:$J i (s_i) a Q(s_i, a)|{a=_(s_i)}$15. 软更新目标网络:

16. end for
end for

关键点: - 第 8 行:确定性策略+探索噪声(通常是 Ornstein-Uhlenbeck 过程) - 第 12 行:目标网络计算 TD 目标,注意动作也是目标网络给出 - 第 15 行:软更新,每步更新一点点(),比 DQN 的硬更新更平滑

TD3:双延迟 DDPG

DDPG 有个严重问题:Q 值过估计。原因类似 DQN ——目标中, 是由 Actor 选择的,而 Actor 训练时又依赖 Q 值,两者相互强化,导致 Q 值螺旋上升。

TD3(Twin Delayed DDPG, Fujimoto et al., 2018)引入三个技巧缓解这个问题:

技巧 1:Clipped Double Q-Learning

学习两个 Critic,取较小值作为目标:

y = r + {i=1,2} Q{'i}(s', {'}(s')) $$

直觉:两个独立估计都过估计的概率较小,取最小值偏保守,抑制过估计。

技巧 2:Delayed Policy Updates

Actor 的更新频率低于 Critic ——每更新 2 次 Critic 才更新 1 次 Actor 。原因是:Critic 需要先收敛到较准确的 Q 值,Actor 才能根据准确的 Q 值优化。如果两者同步更新,Actor 可能利用 Critic 的误差,学到错误的策略。

技巧 3:Target Policy Smoothing

在计算目标时,对目标动作加噪声:

a' = _{'}(s') + , ((0, ), -c, c)

y = r + {i=1,2} Q{'_i}(s', a') $$

直觉:平滑后的目标不会因为单个动作的 Q 值异常而剧烈波动,类似正则化。

完整算法太长,这里给出核心代码:

class TD3:
    def __init__(self, state_dim, action_dim, max_action):
        # Actor
        self.actor = Actor(state_dim, action_dim, max_action)
        self.actor_target = Actor(state_dim, action_dim, max_action)
        self.actor_target.load_state_dict(self.actor.state_dict())
        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=3e-4)
        
        # 两个 Critic
        self.critic_1 = Critic(state_dim, action_dim)
        self.critic_2 = Critic(state_dim, action_dim)
        self.critic_1_target = Critic(state_dim, action_dim)
        self.critic_2_target = Critic(state_dim, action_dim)
        self.critic_1_target.load_state_dict(self.critic_1.state_dict())
        self.critic_2_target.load_state_dict(self.critic_2.state_dict())
        self.critic_optimizer = optim.Adam(
            list(self.critic_1.parameters()) + list(self.critic_2.parameters()), 
            lr=3e-4
        )
        
        self.max_action = max_action
        self.total_it = 0
    
    def select_action(self, state):
        state = torch.FloatTensor(state).unsqueeze(0)
        return self.actor(state).cpu().data.numpy().flatten()
    
    def train(self, replay_buffer, batch_size=256):
        self.total_it += 1
        
        # 采样
        state, action, reward, next_state, done = replay_buffer.sample(batch_size)
        
        with torch.no_grad():
            # Target policy smoothing
            noise = (torch.randn_like(action) * 0.2).clamp(-0.5, 0.5)
            next_action = (self.actor_target(next_state) + noise).clamp(-self.max_action, self.max_action)
            
            # Clipped Double Q-Learning
            target_Q1 = self.critic_1_target(next_state, next_action)
            target_Q2 = self.critic_2_target(next_state, next_action)
            target_Q = torch.min(target_Q1, target_Q2)
            target_Q = reward + (1 - done) * 0.99 * target_Q
        
        # 更新 Critic
        current_Q1 = self.critic_1(state, action)
        current_Q2 = self.critic_2(state, action)
        critic_loss = F.mse_loss(current_Q1, target_Q) + F.mse_loss(current_Q2, target_Q)
        
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()
        
        # Delayed policy updates
        if self.total_it % 2 == 0:
            # 更新 Actor
            actor_loss = -self.critic_1(state, self.actor(state)).mean()
            
            self.actor_optimizer.zero_grad()
            actor_loss.backward()
            self.actor_optimizer.step()
            
            # 软更新目标网络
            for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
                target_param.data.copy_(0.005 * param.data + 0.995 * target_param.data)
            
            for param, target_param in zip(self.critic_1.parameters(), self.critic_1_target.parameters()):
                target_param.data.copy_(0.005 * param.data + 0.995 * target_param.data)
            
            for param, target_param in zip(self.critic_2.parameters(), self.critic_2_target.parameters()):
                target_param.data.copy_(0.005 * param.data + 0.995 * target_param.data)

TD3 在 MuJoCo 连续控制任务上超越了 DDPG,成为 off-policy 连续控制的基准算法。

信任域方法:TRPO 与 PPO

策略更新的困境

策略梯度方法有个根本问题:学习率难调。太小,训练慢;太大,新策略可能比旧策略差很多(毕竟梯度只是局部信息),导致性能崩溃。

一个改进思路是:限制每次更新的步长,确保新策略与旧策略"不太远"。但怎么衡量"距离"?欧氏距离不合适,因为参数空间的距离不等于策略空间的距离。

信任域方法(Trust Region Methods)用 KL 散度衡量策略之间的距离:

D_{} ({{} } | {{} }) = _{s} $$

并限制(如)。

TRPO:严格的信任域优化

TRPO(Trust Region Policy Optimization, Schulman et al., 2015)将策略优化写成约束优化问题:

目标函数中的是重要性采样权重,允许用旧策略的数据更新新策略(off-policy)。

TRPO 用共轭梯度法求解这个约束优化问题,理论上保证单调改进(新策略不会比旧策略差)。但实现复杂,计算昂贵。

PPO:简化的信任域

PPO(Proximal Policy Optimization, Schulman et al., 2017)简化 TRPO,用裁剪(clipping)替代 KL 约束:

L^{} () = $$

其中: - 是重要性采样权重 - 将裁剪到区间(如)

直觉: - 如果(好动作),希望增大,即增大。但裁剪限制,防止增长过快。 - 如果(坏动作),希望减小,即减小。但裁剪限制,防止减小过快。

PPO 的优势: - 实现简单,只需在损失函数中加裁剪 - 不需要计算 KL 散度或 Hessian 矩阵 - 性能接近 TRPO,但速度更快

PPO 已成为工业界最常用的策略梯度算法,OpenAI 、 DeepMind 等都广泛使用。

完整 PPO 实现

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import gym
import numpy as np

class PPOActorCritic(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=64):
        super(PPOActorCritic, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.actor = nn.Linear(hidden_dim, action_dim)
        self.critic = nn.Linear(hidden_dim, 1)
    
    def forward(self, state):
        x = F.tanh(self.fc1(state))
        x = F.tanh(self.fc2(x))
        action_probs = F.softmax(self.actor(x), dim=-1)
        state_value = self.critic(x)
        return action_probs, state_value

class PPO:
    def __init__(self, state_dim, action_dim, lr=3e-4, gamma=0.99, 
                 eps_clip=0.2, K_epochs=10):
        self.gamma = gamma
        self.eps_clip = eps_clip
        self.K_epochs = K_epochs
        
        self.policy = PPOActorCritic(state_dim, action_dim)
        self.optimizer = optim.Adam(self.policy.parameters(), lr=lr)
        self.policy_old = PPOActorCritic(state_dim, action_dim)
        self.policy_old.load_state_dict(self.policy.state_dict())
        
        self.MseLoss = nn.MSELoss()
    
    def select_action(self, state):
        with torch.no_grad():
            state = torch.FloatTensor(state).unsqueeze(0)
            action_probs, _ = self.policy_old(state)
            dist = Categorical(action_probs)
            action = dist.sample()
            action_logprob = dist.log_prob(action)
        
        return action.item(), action_logprob.item()
    
    def update(self, memory):
        # 蒙特卡洛估计回报
        rewards = []
        discounted_reward = 0
        for reward, is_terminal in zip(reversed(memory.rewards), reversed(memory.is_terminals)):
            if is_terminal:
                discounted_reward = 0
            discounted_reward = reward + (self.gamma * discounted_reward)
            rewards.insert(0, discounted_reward)
        
        # 归一化
        rewards = torch.tensor(rewards, dtype=torch.float32)
        rewards = (rewards - rewards.mean()) / (rewards.std() + 1e-7)
        
        # 转换为 tensor
        old_states = torch.FloatTensor(memory.states)
        old_actions = torch.LongTensor(memory.actions)
        old_logprobs = torch.FloatTensor(memory.logprobs)
        
        # 优化 K 个 epoch
        for _ in range(self.K_epochs):
            # 评估动作和状态
            action_probs, state_values = self.policy(old_states)
            dist = Categorical(action_probs)
            action_logprobs = dist.log_prob(old_actions)
            dist_entropy = dist.entropy()
            
            state_values = state_values.squeeze()
            
            # 重要性采样权重
            ratios = torch.exp(action_logprobs - old_logprobs.detach())
            
            # 优势
            advantages = rewards - state_values.detach()
            
            # PPO 损失
            surr1 = ratios * advantages
            surr2 = torch.clamp(ratios, 1-self.eps_clip, 1+self.eps_clip) * advantages
            
            loss = -torch.min(surr1, surr2) + 0.5*self.MseLoss(state_values, rewards) - 0.01*dist_entropy
            
            # 更新
            self.optimizer.zero_grad()
            loss.mean().backward()
            self.optimizer.step()
        
        # 复制新权重到 old policy
        self.policy_old.load_state_dict(self.policy.state_dict())

class Memory:
    def __init__(self):
        self.actions = []
        self.states = []
        self.logprobs = []
        self.rewards = []
        self.is_terminals = []
    
    def clear_memory(self):
        del self.actions[:]
        del self.states[:]
        del self.logprobs[:]
        del self.rewards[:]
        del self.is_terminals[:]

def train_ppo(env_name='CartPole-v1', max_episodes=1000, 
              update_timestep=200):
    env = gym.make(env_name)
    state_dim = env.observation_space.shape[0]
    action_dim = env.action_space.n
    
    ppo = PPO(state_dim, action_dim)
    memory = Memory()
    
    timestep = 0
    episode_rewards = []
    
    for episode in range(max_episodes):
        state = env.reset()
        episode_reward = 0
        
        for t in range(500):
            timestep += 1
            
            # 选择动作
            action, action_logprob = ppo.select_action(state)
            next_state, reward, done, _ = env.step(action)
            
            # 存储
            memory.states.append(state)
            memory.actions.append(action)
            memory.logprobs.append(action_logprob)
            memory.rewards.append(reward)
            memory.is_terminals.append(done)
            
            state = next_state
            episode_reward += reward
            
            # 更新
            if timestep % update_timestep == 0:
                ppo.update(memory)
                memory.clear_memory()
            
            if done:
                break
        
        episode_rewards.append(episode_reward)
        
        if (episode + 1) % 50 == 0:
            avg_reward = np.mean(episode_rewards[-50:])
            print(f"Episode {episode+1}, Avg Reward: {avg_reward:.2f}")
    
    return ppo, episode_rewards

# 训练
ppo, rewards = train_ppo(max_episodes=1000)

PPO 通常在 100-200 个 episode 内解决 CartPole,且训练曲线非常平滑(相比 REINFORCE)。

最大熵强化学习:SAC

熵正则化的动机

传统 RL 的目标是最大化期望回报。但这有个问题:策略可能过早收敛到局部最优,缺乏探索。

一个改进思路是鼓励策略的"多样性"——不要总是选择同一个动作,而是保持一定的随机性。衡量随机性的指标是熵(entropy):

H((|s)) = -_a (a|s) (a|s) $$

熵越大,策略越随机;熵为 0,策略完全确定。

最大熵强化学习的目标是:

J() = t {(s_t, a_t) _} [r(s_t, a_t) + H((|s_t))] $$

其中是温度系数,控制熵的权重。这个目标鼓励策略在最大化回报的同时保持探索。

好处: - 自动探索:不需要人工设计探索策略(如-greedy) - 鲁棒性:策略更平滑,对环境扰动不敏感 - 避免局部最优:熵惩罚阻止策略过早收敛

SAC:Soft Actor-Critic

SAC(Soft Actor-Critic, Haarnoja et al., 2018)是最大熵框架下的 off-policy 算法,结合了: - Actor-Critic 架构 - 经验回放和目标网络(like DDPG) - 熵正则化

核心思想:

Soft Q-function: Q 值包含熵奖励

Q^{} (s,a) = r + _{s', a'} [Q(s', a') + H((|s'))] $$

策略更新: 最大化 Q 值+熵

自动调节温度: 不是固定的,而是根据目标熵自动调节

伪代码(简化):

算法:SAC

初始化 Actor, 两个 Critic, 温度$ $初始化目标$ Q_{'1}, Q{'_2}= 1, 2, $do
采样动作,执行并存储5. 从 buffer 采样6. 采样,计算目标: $$

y_i = r_i + ({j=1,2} Q{'_j}(s'_i, a'i) - (a'_i|s'i))$$7. 更新 Critic:$Q = i (y_i - Q{j}(s_i, a_i))^2$8. 更新 Actor:$= {s , a } [(a|s) - Q{_1}(s,a)]$9. 更新温度:(目标熵) 10. 软更新目标网络 11. end for

SAC 在连续控制任务上表现出色,兼具样本效率(off-policy)和稳定性(最大熵),被广泛应用于机器人控制。

代码框架

完整的 SAC 实现较长(约 500 行),这里展示核心部分:

class SAC:
    def __init__(self, state_dim, action_dim, max_action):
        self.actor = GaussianPolicy(state_dim, action_dim, max_action)
        self.critic_1 = QNetwork(state_dim, action_dim)
        self.critic_2 = QNetwork(state_dim, action_dim)
        self.critic_1_target = QNetwork(state_dim, action_dim)
        self.critic_2_target = QNetwork(state_dim, action_dim)
        
        # 自动调节温度
        self.target_entropy = -action_dim
        self.log_alpha = torch.zeros(1, requires_grad=True)
        self.alpha = self.log_alpha.exp()
        
        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=3e-4)
        self.critic_optimizer = optim.Adam(
            list(self.critic_1.parameters()) + list(self.critic_2.parameters()), 
            lr=3e-4
        )
        self.alpha_optimizer = optim.Adam([self.log_alpha], lr=3e-4)
    
    def select_action(self, state, evaluate=False):
        state = torch.FloatTensor(state).unsqueeze(0)
        if evaluate:
            _, _, action = self.actor.sample(state)
        else:
            action, _, _ = self.actor.sample(state)
        return action.detach().cpu().numpy()[0]
    
    def train(self, replay_buffer, batch_size=256):
        state, action, reward, next_state, done = replay_buffer.sample(batch_size)
        
        with torch.no_grad():
            # 采样下一个动作
            next_action, next_log_prob, _ = self.actor.sample(next_state)
            
            # 计算目标 Q 值(包含熵)
            target_Q1 = self.critic_1_target(next_state, next_action)
            target_Q2 = self.critic_2_target(next_state, next_action)
            target_Q = torch.min(target_Q1, target_Q2) - self.alpha * next_log_prob
            target_Q = reward + (1 - done) * 0.99 * target_Q
        
        # 更新 Critic
        current_Q1 = self.critic_1(state, action)
        current_Q2 = self.critic_2(state, action)
        critic_loss = F.mse_loss(current_Q1, target_Q) + F.mse_loss(current_Q2, target_Q)
        
        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_optimizer.step()
        
        # 更新 Actor
        new_action, log_prob, _ = self.actor.sample(state)
        Q1_new = self.critic_1(state, new_action)
        Q2_new = self.critic_2(state, new_action)
        Q_new = torch.min(Q1_new, Q2_new)
        
        actor_loss = (self.alpha * log_prob - Q_new).mean()
        
        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        self.actor_optimizer.step()
        
        # 更新温度参数
        alpha_loss = -(self.log_alpha * (log_prob + self.target_entropy).detach()).mean()
        
        self.alpha_optimizer.zero_grad()
        alpha_loss.backward()
        self.alpha_optimizer.step()
        
        self.alpha = self.log_alpha.exp()
        
        # 软更新目标网络
        for param, target_param in zip(self.critic_1.parameters(), self.critic_1_target.parameters()):
            target_param.data.copy_(0.005 * param.data + 0.995 * target_param.data)
        
        for param, target_param in zip(self.critic_2.parameters(), self.critic_2_target.parameters()):
            target_param.data.copy_(0.005 * param.data + 0.995 * target_param.data)

SAC 在 MuJoCo 任务上通常优于 TD3 和 PPO,是目前连续控制的顶尖算法之一。

算法对比与选择指南

主要算法对比

算法	类型	动作空间	样本效率	稳定性	实现难度	适用场景
REINFORCE	On-policy	离散/连续	低	中	易	简单任务,教学用
A2C/A3C	On-policy	离散/连续	中	中	中	Atari,并行环境
PPO	On-policy	离散/连续	中	高	中	通用,工业界首选
TRPO	On-policy	离散/连续	中	高	难	理论研究
DDPG	Off-policy	连续	高	低	中	连续控制,已被 TD3 取代
TD3	Off-policy	连续	高	中	中	连续控制,样本效率重要
SAC	Off-policy	连续	高	高	难	连续控制,追求性能

选择建议

1. 根据动作空间: - 离散动作:PPO(首选)、 A2C 、 DQN - 连续动作:SAC(首选)、 TD3 、 PPO

2. 根据样本预算: - 样本昂贵(如真实机器人):SAC 、 TD3(off-policy,高样本效率) - 样本充足(如模拟器):PPO(更稳定)

3. 根据实现资源: - 快速原型:PPO(OpenAI Baselines 、 Stable Baselines 都有现成实现) - 从零实现:REINFORCE 或 A2C(代码简单)

4. 根据任务特点: - 稀疏奖励:SAC(熵鼓励探索) - 稠密奖励:PPO 或 TD3 - 部分可观测:LSTM+A2C 或 PPO - 多智能体:MADDPG(TD3 的多智能体版本)

5. 工业应用: - OpenAI 、 DeepMind:PPO 用于大规模训练(如 Dota 2 、 StarCraft II) - 机器人控制:SAC(Berkeley RL lab 推荐) - 自动驾驶:SAC 或 TD3

深度 Q&A

Q1:为什么 Policy Gradient 能处理连续动作而 DQN 不能?

A:根本区别在于策略的表示方式。 DQN 学习 Q 函数,通过隐式得到策略。在离散空间(如 18 个动作),枚举所有计算并取最大值很简单。但在连续空间(如机器人 7 个关节角度),需要求解:

这是一个连续优化问题,没有解析解,需要迭代算法(如梯度上升)求解。每次选择动作都要运行优化器,计算昂贵且不精确。

Policy Gradient 方法直接参数化策略: - 离散动作:输出 Softmax 分布,采样或取 argmax - 连续动作:输出高斯分布的均值和方差,采样一次前向传播就得到动作,无需优化,天然支持连续空间。

Q2:为什么 REINFORCE 方差大?如何降低?

A:REINFORCE 用完整回报估计 Q 值,方差来源于:

轨迹随机性:不同轨迹的可能差异很大
长期累积:误差沿时间累积, 越大方差越大

降低方差的方法:

方法 1:Baseline 减去状态价值,只保留优势。是该状态的"平均"回报,减去后消除状态本身的好坏,只关注动作的相对优劣。实验表明方差可降低 50%-90%。

方法 2:Critic(Actor-Critic) 用函数逼近或替代蒙特卡洛估计,引入偏差但大幅降低方差。 TD 方法只依赖一步转移,方差远小于。

方法 3:多步 return 用 n-step return 折中偏差和方差。是 TD(低方差高偏差), 是蒙特卡洛(高方差低偏差)。实践中到效果好。

方法 4:GAE(Generalized Advantage Estimation) 指数加权多步 TD 误差:

A_t^{} = {l=0}^{} ()^l {t+l} $$ 控制偏差-方差权衡。 PPO 常用。

Q3:PPO 的裁剪机制如何工作?

A:PPO 的目标是:

L^{} = [(r_t() A_t, (r_t, 1-, 1+) A_t)] $$

其中是新旧策略的概率比。

情况 1:(好动作,希望增大概率) - 如果:取的第一项,正常增大 - 如果:取第二项,梯度为 0(因为 clip 是常数),停止增大

直觉:好动作的概率不能增长过快,最多到旧策略的倍(如 1.2 倍)。

情况 2:(坏动作,希望减小概率) - 如果:取第一项(注意,所以是减小) - 如果:取第二项,梯度为 0,停止减小

直觉:坏动作的概率不能减小过快,最少到旧策略的倍(如 0.8 倍)。

这个机制确保新策略与旧策略的 KL 散度不会太大,避免"一步跨太大"导致性能崩溃。

Q4:DDPG 与 TD3 的核心区别?

A:TD3 在 DDPG 基础上加三个技巧解决 Q 值过估计:

1. Clipped Double Q-Learning - DDPG:单个 Critic,目标 - TD3:两个 Critic,目标取最小值抑制过估计。原因:两个独立的 Q 网络同时过估计同一动作的概率较小,最小值偏保守。

2. Delayed Policy Updates - DDPG:Actor 和 Critic 同步更新,每步都更新 - TD3:Critic 更新 2 次,Actor 才更新 1 次

原因:Critic 需要先收敛到准确的 Q 值,Actor 才能根据准确的梯度优化。如果同步更新,Actor 可能利用 Critic 的误差学到错误策略。

3. Target Policy Smoothing - DDPG:目标动作 - TD3: 加噪声平滑 Q 函数,避免单个动作的 Q 值异常导致目标剧烈波动。

实验表明,三个技巧都重要,组合后 TD3 在 MuJoCo 上全面超越 DDPG,成为新的 off-policy 连续控制基准。

Q5:SAC 的自动温度调节如何工作?

A:SAC 的目标是:

J() = [_t r_t + H((|s_t))] $$

温度控制熵的权重: 大,策略更随机(探索); 小,策略更确定(利用)。

早期 SAC 手动设置,但不同任务最优的差异很大。后续工作(Haarnoja et al., 2018)提出自动调节:

目标熵约束:设定目标熵(如,负的动作维度),要求:

即策略的平均熵不低于目标。

对偶优化:引入拉格朗日乘子,优化问题变为:

对求导:

- 如果当前策略熵(太随机),增大惩罚熵,迫使策略更确定 - 如果(太确定),减小鼓励探索

实现中, 保证非负,优化:

注意,所以就是负熵。

这样会自动调节到使策略熵接近目标的值,无需人工调参。

Q6:为什么 PPO 比 TRPO 更流行?

A:TRPO 理论上更严格(单调改进保证),但实践中 PPO 更受欢迎,原因:

1. 实现简单 - TRPO:需要计算 Hessian 矩阵的逆或用共轭梯度法,涉及二阶优化,代码复杂(约 1000 行) - PPO:只需修改损失函数加入 clip,一阶优化(Adam),代码简单(约 200 行)

2. 计算效率 - TRPO:共轭梯度法每次迭代需要多次 Hessian-向量乘法,计算昂贵 - PPO:标准梯度下降,速度快 2-3 倍

3. 性能相当 实验表明,PPO 在多数任务上性能接近或超过 TRPO 。 PPO 的 clip 机制虽然是启发式的,但实践中很有效。

4. 超参数鲁棒 - TRPO:对 KL 约束的选择敏感,需要仔细调参 - PPO:clip 范围在多数任务上都 work,鲁棒性好

5. 易于扩展 PPO 的 clip 机制很容易与其他技术结合(如 GAE 、奖励塑形、课程学习),而 TRPO 的约束优化框架不太灵活。

OpenAI 在训练 Dota 2 AI 和 ChatGPT 的 RLHF 阶段都使用 PPO,验证了其大规模应用的可行性。

Q7:on-policy vs off-policy,各有什么优缺点?

On-policy(REINFORCE, A2C, PPO, TRPO):

优点: - 稳定性好:训练数据与当前策略匹配,分布一致,梯度估计更准确 - 理论简单:直接优化期望回报,无需重要性采样修正 - 容易实现:不需要经验回放等复杂机制

缺点: - 样本效率低:每条经验只用一次(当前策略生成的),用完就扔 - 难以并行:虽然可以多环境采样(如 A3C),但数据必须来自当前策略 - 探索不足:依赖策略自身的随机性,可能过早收敛

Off-policy(DQN, DDPG, TD3, SAC):

优点: - 样本效率高:经验回放允许多次重用数据,每条经验可用几十次 - 灵活探索:可以用任意探索策略(如-greedy 、 OU 噪声)收集数据 - 支持人类数据:可以从演示或历史数据学习(imitation learning)

缺点: - 训练不稳定:数据分布与目标策略不匹配,需要重要性采样修正或目标网络稳定 - 理论复杂:涉及 off-policy 修正、分布偏移等问题 - 可能发散:函数逼近+off-policy+bootstrapping(deadly triad)容易不收敛

选择建议: - 样本昂贵(如真实机器人):off-policy(SAC 、 TD3) - 样本充足(如模拟器、 Atari):on-policy(PPO) - 需要稳定训练:on-policy - 需要从演示学习:off-policy

Q8:Actor-Critic 中 Actor 和 Critic 如何互相促进?

A:Actor-Critic 是一个迭代改进的过程:

Critic → Actor(评论家指导演员):

Critic 学习价值函数或,评估"状态有多好"或"动作有多好"。 Actor 根据这个评估优化策略: - 如果 Critic 说,Actor 增大,减小 - 策略梯度公式正是体现这一点

这样,Actor 不是盲目试错,而是有方向地改进(朝 Q 值增大的方向)。

Actor → Critic(演员帮助评论家):

Critic 需要数据来学习价值函数。 Actor 生成新的轨迹,提供训练数据: - On-policy:Critic 用当前 Actor 生成的数据,TD 更新 - Off-policy:Critic 用经验回放中的数据,覆盖更广的状态空间

更重要的是,Actor 的改进使策略更优,Critic 能访问到更高价值的状态,学习到更准确的价值函数(正样本增多)。

正反馈循环:

好的 Critic → Actor 改进更快 → 访问更好的状态 → Critic 学得更准 → Actor 进一步改进

这个循环最终收敛到最优策略和最优价值函数(理论上,实践中可能收敛到局部最优)。

关键是平衡两者的学习速率: - 如果 Actor 学太快,Critic 跟不上,提供错误的价值估计,Actor 学偏 - 如果 Critic 学太快,Actor 更新太慢,浪费准确的价值信息

通常设置 Actor 学习率 < Critic 学习率(如),让 Critic 先学好。

Q9:如何选择折扣因子?

A:折扣因子控制对未来奖励的重视程度: - :只关心即时奖励(短视) - :未来奖励与即时奖励同等重要(远见)

理论考虑:

任务时长:
- 短期任务(如 CartPole,几十步结束): 到 - 长期任务(如 Atari 某些游戏,几千步): 或 - 无限时域任务: 必须保证回报有界
有效时域:折扣因子决定"有效规划长度" - :有效长度步
- :有效长度步
- :有效长度 1000 步
如果任务需要 100 步规划,但,智能体最多看 10 步,学不到长期策略。
方差与偏差:
- 大:回报方差大(累积更多随机性),但偏差小(准确反映长期价值)
- 小:方差小,但短视(低估长期价值)

实践建议:

先用(常见默认值)
如果训练不稳定(方差大),适当减小(如 0.95)
如果任务明显需要长期规划但智能体学不到,增大(如 0.995 或 0.999)
某些任务可以用变化的(课程学习):初期小快速学到短期策略,后期增大学长期规划

示例: - CartPole:(任务短,但 0.99 已足够) - Atari Pong:(一局几百步,需要预判球的轨迹) - Go(围棋):(或极接近 1,如 0.9999),因为要规划全局

Q10:如何调试策略梯度算法?

A:策略梯度算法调试比监督学习难,因为奖励信号稀疏且延迟。系统化调试流程:

1. 检查环境和数据 - 随机策略的平均回报:如果比智能体还好,说明智能体有问题 - 手动策略的回报:人类专家能达到多少?上界在哪里? - 奖励分布:检查是否有异常值(如突然的+1000),可能导致训练不稳定

2. 简化问题验证代码 - 在简单环境测试(如 CartPole):应该 100-200 episodes 内解决 - 如果简单环境都不 work,代码有 bug(检查梯度计算、优势估计等)

3. 监控关键指标 - 策略熵:应该逐渐下降(策略从随机变确定),但不要太快降到 0(过早收敛) - 优势的均值和方差:均值应接近 0(baseline 有效),方差应逐渐减小 - 价值函数误差: 应逐渐减小,如果长期很大,Critic 没学好 - KL 散度(PPO/TRPO):每次更新的应在目标范围(如 0.01-0.05)

4. 可视化策略行为 - 渲染几个 episode,看智能体在做什么:是随机游走?还是有明确策略? - 检查动作分布:是否某些动作从不选择?(可能网络初始化问题)

5. 检查超参数 - 学习率太大:训练曲线剧烈震荡 - 学习率太小:收敛极慢 - Batch size 太小:梯度估计方差大,不稳定 - 太小:短视,学不到长期策略

6. 常见 bug - 忘记 detach target:价值函数的目标或 TD target 不应该有梯度 - 优势未归一化: 的 scale 影响学习,最好归一化 - 奖励未裁剪:某些环境奖励 scale 差异大,需要 normalize 或 clip - 探索不足:确定性策略没有加噪声,或噪声太小 - 梯度爆炸:需要 gradient clipping

7. 对比 baseline - 用 Stable Baselines3 等成熟库跑同样任务,对比性能 - 如果库的结果好得多,说明自己实现有问题 - 如果库也不 work,可能是任务太难或超参数需要特殊调整

8. 逐步增加复杂度 - 先用最简单的 REINFORCE 验证环境和数据流 - 再加 baseline,检查方差是否降低 - 再升级到 A2C,检查 Critic 是否有效 - 最后升级到 PPO/SAC 等,享受性能提升

调试强化学习需要耐心和系统化方法,建议用 tensorboard 等工具记录所有指标,方便对比和回溯。

参考文献

以下是 Policy Gradient 和 Actor-Critic 领域的核心论文:

Williams, R. J. (1992). Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning, 8(3-4), 229-256.
论文链接
REINFORCE 算法,策略梯度方法的开创性工作
Sutton, R. S., McAllester, D. A., Singh, S. P., & Mansour, Y. (2000). Policy gradient methods for reinforcement learning with function approximation. NIPS.
论文链接
策略梯度定理的严格证明
Silver, D., Lever, G., Heess, N., et al. (2014). Deterministic policy gradient algorithms. ICML.
论文链接
确定性策略梯度,DDPG 的理论基础
Mnih, V., Badia, A. P., Mirza, M., et al. (2016). Asynchronous methods for deep reinforcement learning. ICML.
arXiv:1602.01783
A3C 算法,首个在 Atari 上与 DQN 竞争的 on-policy 方法
Schulman, J., Levine, S., Abbeel, P., et al. (2015). Trust region policy optimization. ICML.
arXiv:1502.05477
TRPO,引入信任域约束保证单调改进
Lillicrap, T. P., Hunt, J. J., Pritzel, A., et al. (2016). Continuous control with deep reinforcement learning. ICLR.
arXiv:1509.02971
DDPG,将 DQN 扩展到连续动作空间
Schulman, J., Wolski, F., Dhariwal, P., et al. (2017). Proximal policy optimization algorithms.
arXiv:1707.06347
PPO,工业界最常用的策略梯度算法
Fujimoto, S., van Hoof, H., & Meger, D. (2018). Addressing function approximation error in actor-critic methods. ICML.
arXiv:1802.09477
TD3,解决 DDPG 的 Q 值过估计问题
Haarnoja, T., Zhou, A., Abbeel, P., & Levine, S. (2018). Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. ICML.
arXiv:1801.01290
SAC,最大熵框架下的 off-policy 算法
Haarnoja, T., Zhou, A., Hartikainen, K., et al. (2018). Soft actor-critic algorithms and applications.
arXiv:1812.05905
SAC 的应用和自动温度调节
Schulman, J., Moritz, P., Levine, S., et al. (2016). High-dimensional continuous control using generalized advantage estimation. ICLR.
arXiv:1506.02438
GAE,降低策略梯度方差的重要技术

从 REINFORCE 的蒙特卡洛策略梯度到 Actor-Critic 的 TD 方法,从 A3C 的异步并行到 PPO 的裁剪技巧,从 DDPG 的确定性策略到 SAC 的最大熵框架——策略梯度方法在过去三十年发展出了丰富的技术栈。这些算法不仅突破了 DQN 的离散动作限制,在连续控制任务中大放异彩,也在探索-利用平衡、样本效率、训练稳定性等方面提供了多样化的解决方案。 PPO 凭借简单性和鲁棒性成为工业界首选,SAC 和 TD3 则在对性能要求极高的机器人控制中占据统治地位。

然而,model-free 方法的样本效率仍然是瓶颈——即使是最先进的 SAC,在复杂任务上也需要数百万次交互。下一章我们将探索 model-based 方法:通过学习环境模型并在模型中规划,大幅减少与真实环境的交互次数,这将引领我们进入 Dyna 、 MuZero 、 Dreamer 等算法的世界。