强化学习（一）—— 基础与核心概念

一个智能体要如何在环境中学习最优行为？当 AlphaGo 在围棋盘上击败人类顶尖选手，当机器人学会走路和抓取物体，当推荐系统根据用户反馈不断优化推荐策略——这些背后都有一个共同的数学框架：强化学习。

强化学习不同于监督学习的"有标注数据就能训练"，也不同于无监督学习的"寻找数据内在结构"。它面对的是一个更接近真实世界的问题：在没有明确正确答案的情况下，通过试错和奖励反馈，学习长期最优的决策策略。

从骑自行车说起：强化学习的直觉

学习骑自行车是经典的强化学习过程。没有人会给你一本"标准骑行手册"，告诉你在每个时刻应该如何调整把手和身体重心（没有监督学习的标签）。你需要自己尝试：稍微向左倾斜，车往左偏了；身体向右调整，车又往右偏。摔倒了是负反馈，保持平衡是正反馈。

经过数百次试错后，你的大脑学会了一套策略：根据当前的车身倾斜角度、速度、路面状况，实时决定如何调整身体和把手。这个策略不是通过背诵得来的，而是通过与环境交互、获得反馈、调整行为这个循环逐步优化的。

强化学习的数学框架就是对这个过程的精确描述。

马尔可夫决策过程：强化学习的数学基础

强化学习的核心是马尔可夫决策过程（ Markov Decision Process, MDP）。 MDP 是一个五元组：

$$ = (S, A, P, R, )

$$

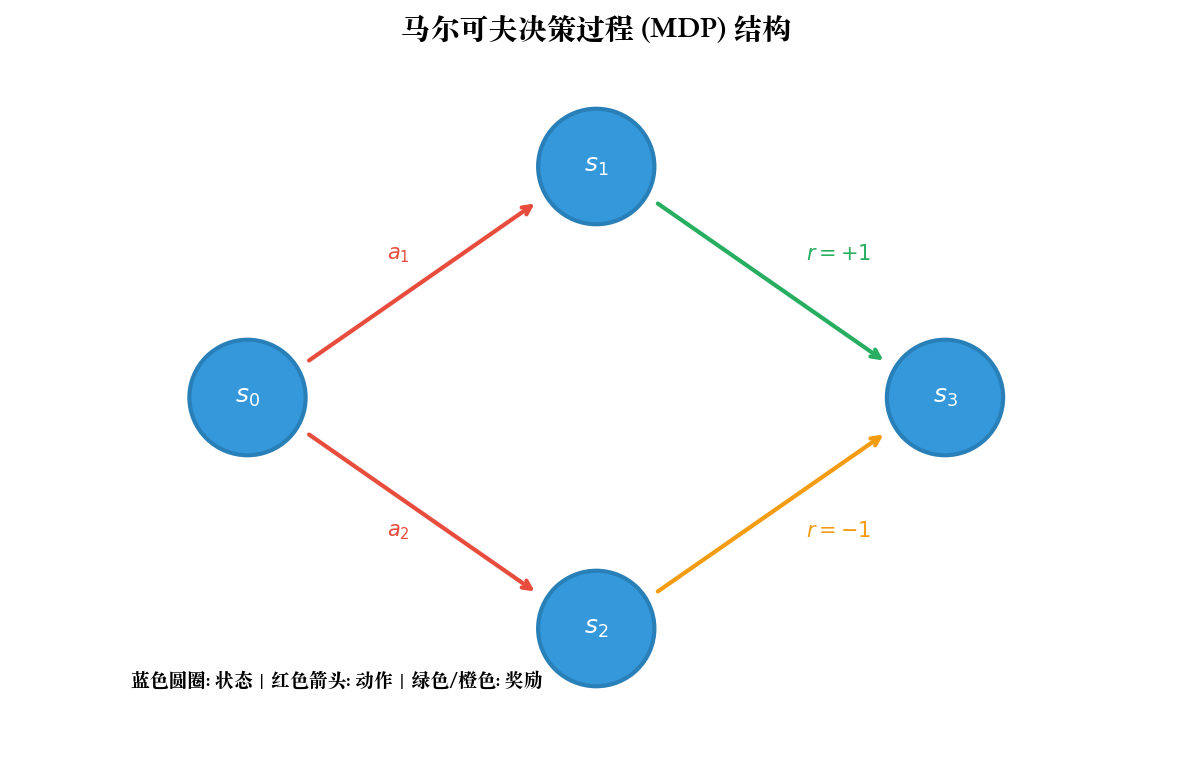
基本要素

状态空间 ：

环境的所有可能状态。在骑自行车中，状态可能包括车身倾斜角度、速度、与障碍物的距离等。状态可以是离散的（如棋盘格子）或连续的（如机器人关节角度）。

动作空间 ：

智能体可以执行的所有动作。可以是离散动作（如向上下左右移动）或连续动作（如施加多大力矩）。

转移概率 ：

在状态 执行动作 后，转移到状态 的概率。转移概率完整定义了环境的动力学：

$$

P: S A S $$

满足概率归一化条件：。

奖励函数 ：

在状态 执行动作 转移到 后获得的即时奖励。奖励是智能体学习的唯一信号。在很多情况下简化为 或 。

折扣因子 ：

衡量未来奖励的重要性。 表示只关心即时奖励， 表示更重视长期回报。

马尔可夫性质

MDP 的核心假设是马尔可夫性：未来只依赖于当前状态，与历史无关。

$$

P(s_{t+1} | s_t, a_t, s_{t-1}, a_{t-1}, , s_0, a_0) = P(s_{t+1} | s_t, a_t) $$

这个假设看似强，但在实践中很实用。如果当前状态包含了所有相关信息（如把最近几帧图像拼接作为状态），马尔可夫性就能满足。

策略：从状态到动作的映射

策略 是智能体的行为准则，定义了在每个状态下如何选择动作：

确定性策略：

$$

a = (s) $$

直接给出动作。

随机策略：

给出动作的概率分布。随机策略在探索和处理部分可观测环境时更有用。

回报与价值函数

为什么需要"累积回报"？一个钓鱼的故事

场景：你在河边钓鱼

决策1：用便宜的鱼饵 - 立即结果：省了5块钱（即时奖励+5） - 长期结果：钓不到鱼，白坐一天（总收益-95）

决策2：用好鱼饵 - 立即结果：花了20块钱（即时奖励-20） - 长期结果：钓到大鱼，卖了200块（总收益+180）

关键洞察：不能只看眼前利益（即时奖励），要看累积回报！

累积回报的数学定义

智能体的目标是最大化累积回报。从时刻 开始的回报定义为：

$$

G_t = R_{t+1} + R_{t+2} + ^2 R_{t+3} + = {k=0}^{} ^k R{t+k+1} $$

符号解释： - ：下一步的即时奖励 - ：折扣因子（0到1之间） - ：两步后的奖励打个折扣 - ：三步后的奖励打更大折扣

为什么要"打折扣"？

类比：钱的时间价值

现在的100元 vs 10年后的100元，你要哪个？当然是现在的！因为： 1. 不确定性：10年太久，可能拿不到 2. 机会成本：现在的100元可以投资增值

在强化学习中也一样：

折扣因子 的作用： - 数学上：保证无限步的回报有界（当 时，） - 直觉上：远期奖励的不确定性更大，应该打折扣 - 实际上：避免智能体过度延迟获取奖励

具体例子： - ：10步后的奖励只值当前的 倍 - ：更看重长期，100步后的奖励还值 倍 - ：极端短视，只看即时奖励

状态价值函数 ：

从状态 开始，遵循策略 ，期望获得的累积回报：

$$

V^(s) = = $$ 衡量"在状态 有多好"（按策略 行动）。

动作价值函数 ：

从状态 执行动作 ，然后遵循策略 ，期望获得的累积回报：

$$

Q^(s, a) = _$$ 衡量"在状态 执行动作 有多好"。

两者的关系：

$$

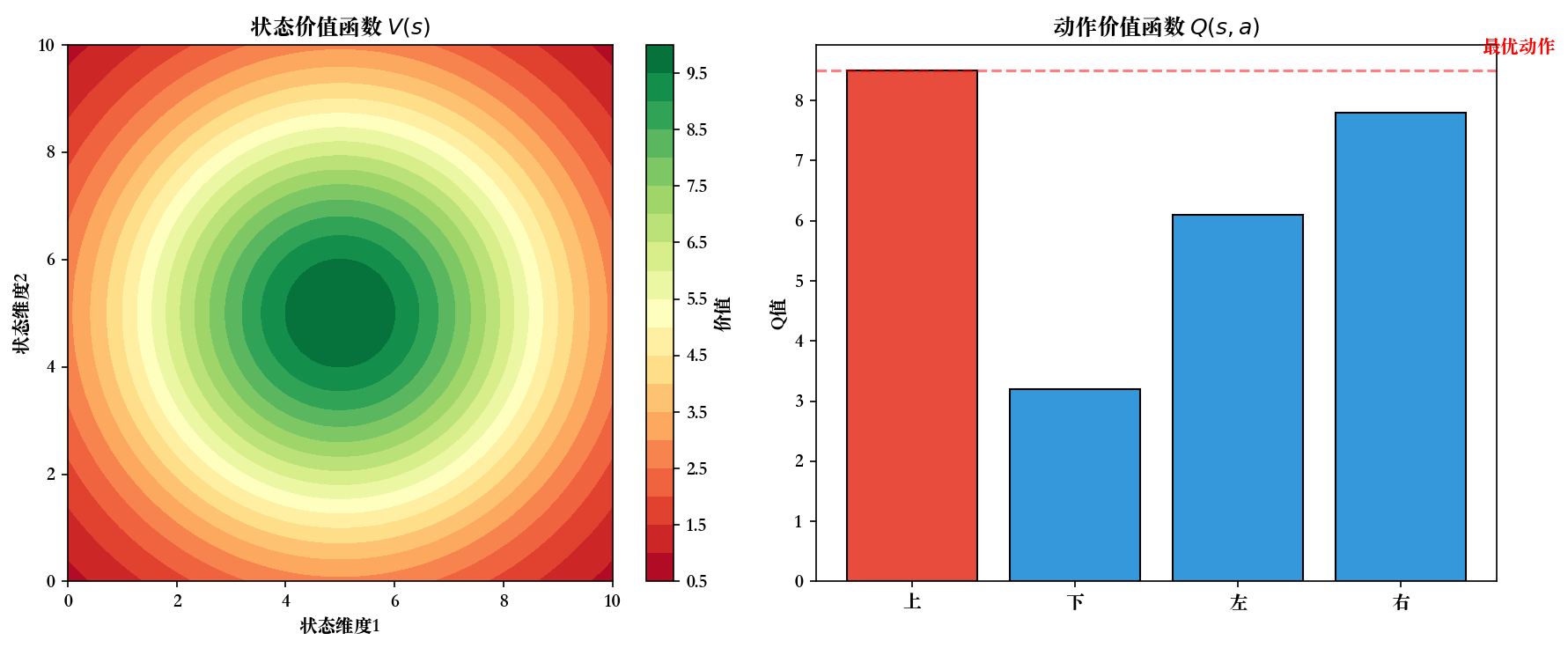
V^(s) = _{a A} (a|s) Q^(s, a)

Q^(s, a) = _{s' S} P(s'|s, a)

$$

Bellman 方程：价值函数的递归结构

价值函数满足递归关系，称为 Bellman 方程。这是强化学习理论的基石。

Bellman 期望方程（对任意策略 ）：

$$

V^(s) = {a A} (a|s) {s' S} P(s'|s, a)

Q^(s, a) = _{s' S} P(s'|s, a) $$

推导逻辑：

当前状态的价值 = 即时奖励的期望 + 下一状态价值的折扣期望。

展开 ：

Bellman 最优方程（对最优策略 ）：

定义最优价值函数：

$$

V^{*}(s) = _V^(s), Q^{*}(s, a) = _Q^(s, a) $$

最优 Bellman 方程：

$$

V^{*}(s) = {a A} {s' S} P(s'|s, a)

Q^{*}(s, a) = _{s' S} P(s'|s, a) $$

最优策略：

数值示例：

考虑一个简单的 2 状态 MDP：

• 状态：
• 动作：（在每个状态都可执行）
• 转移概率和奖励：

			0.5	5
			0.5	10
			0.9	0
			0.1	15
			0.7	2
			0.3	8
			1.0	3

• 折扣因子：
• 策略：（总是选择 ）

计算 ：

$$

V^(s_1) = 0.5 (5 + 0.9 V^(s_1)) + 0.5 (10 + 0.9 V^(s_2))

V^(s_2) = 0.7 (2 + 0.9 V^(s_1)) + 0.3 (8 + 0.9 V^(s_2)) $$

这是两个关于 和 的线性方程组。整理：

$$

V^(s_1) - 0.45 V^(s_1) - 0.45 V^(s_2) = 7.5 -0.63 V^(s_1) + V^(s_2) - 0.27 V^(s_2) = 3.8 $$

即：

求解得：

$$

V^(s_1) , V^(s_2) $$

动态规划方法：已知模型的最优控制

当环境模型（转移概率 和奖励函数 ）已知时，可以用动态规划求解最优策略。

策略评估：计算给定策略的价值函数

给定策略 ，策略评估计算 。

迭代算法：

1. 初始化 （对所有 ）

2. 重复直到收敛：

   对所有 ：

$$

V_{k+1}(s) {a A} (a|s) {s' S} P(s'|s, a) $$

这是 Bellman 期望方程的迭代形式。收敛性由 Banach 不动点定理保证（ Bellman 算子是收缩映射）。

策略改进：根据价值函数改进策略

给定 ，构造贪婪策略：

策略改进定理：贪婪策略 至少不比 差：

$$

V^{'}(s) V^(s), s S $$

证明：

对任意状态 ，按定义有：

$$

Q^(s, '(s)) = _{a} Q^(s, a) Q^(s, (s)) = V^(s) $$

根据 Q 函数的定义：

$$

Q^(s, '(s)) = [R_{t+1} + V^(S_{t+1}) | S_t = s, A_t = '(s)] $$

如果在第一步选择 ，之后遵循 ，获得的回报不少于一直遵循 。如果每步都用贪婪策略，回报会更好。

策略迭代算法

交替进行策略评估和策略改进：

1. 初始化随机策略 2. 策略评估：求解 $V^{k}{k+1}(s) a {s'} P(s'|s, a) [R(s, a, s') + V^{_k}(s')]$4. 如果 ，停止；否则返回步骤 2

策略迭代保证收敛到最优策略 。

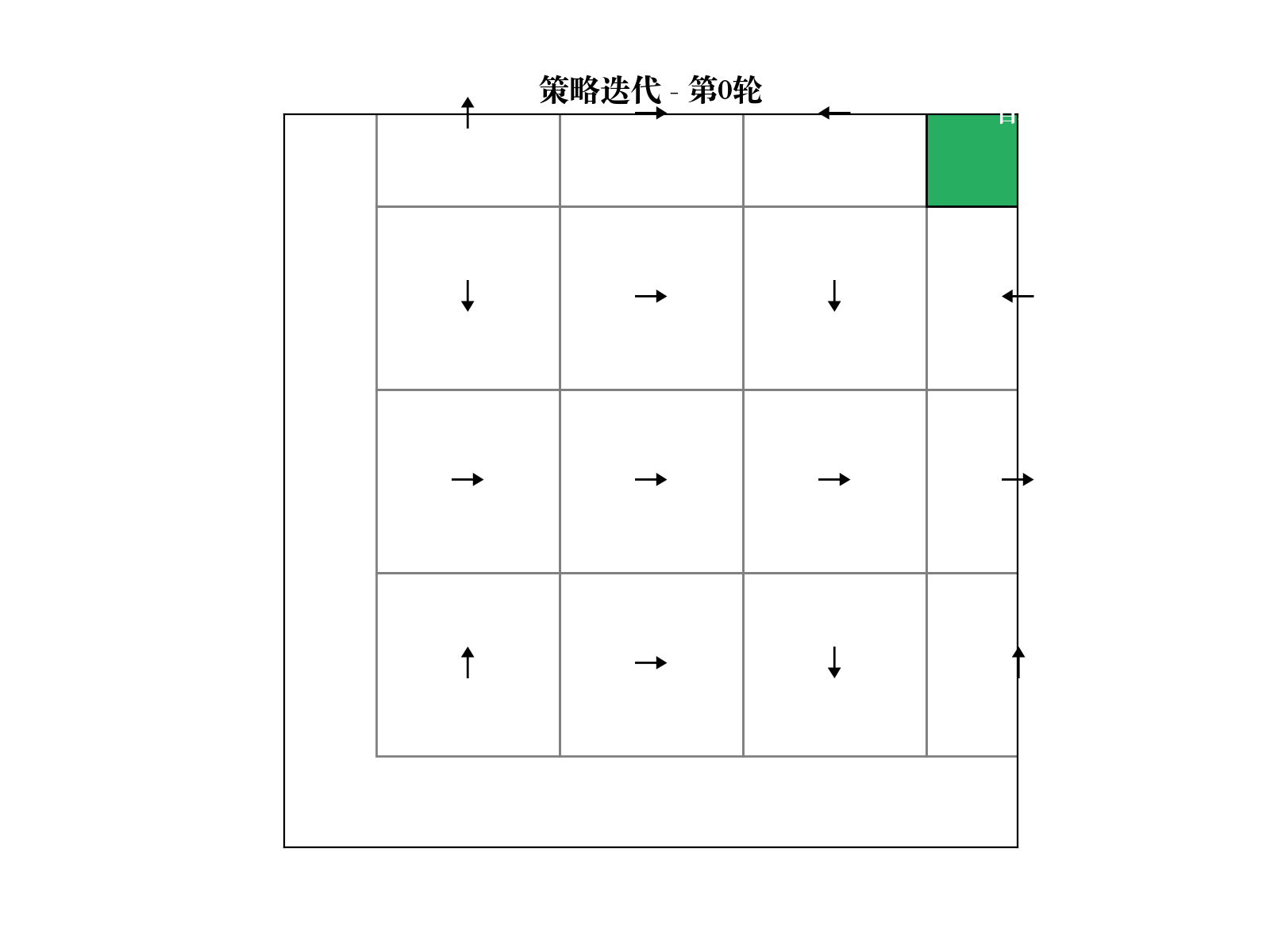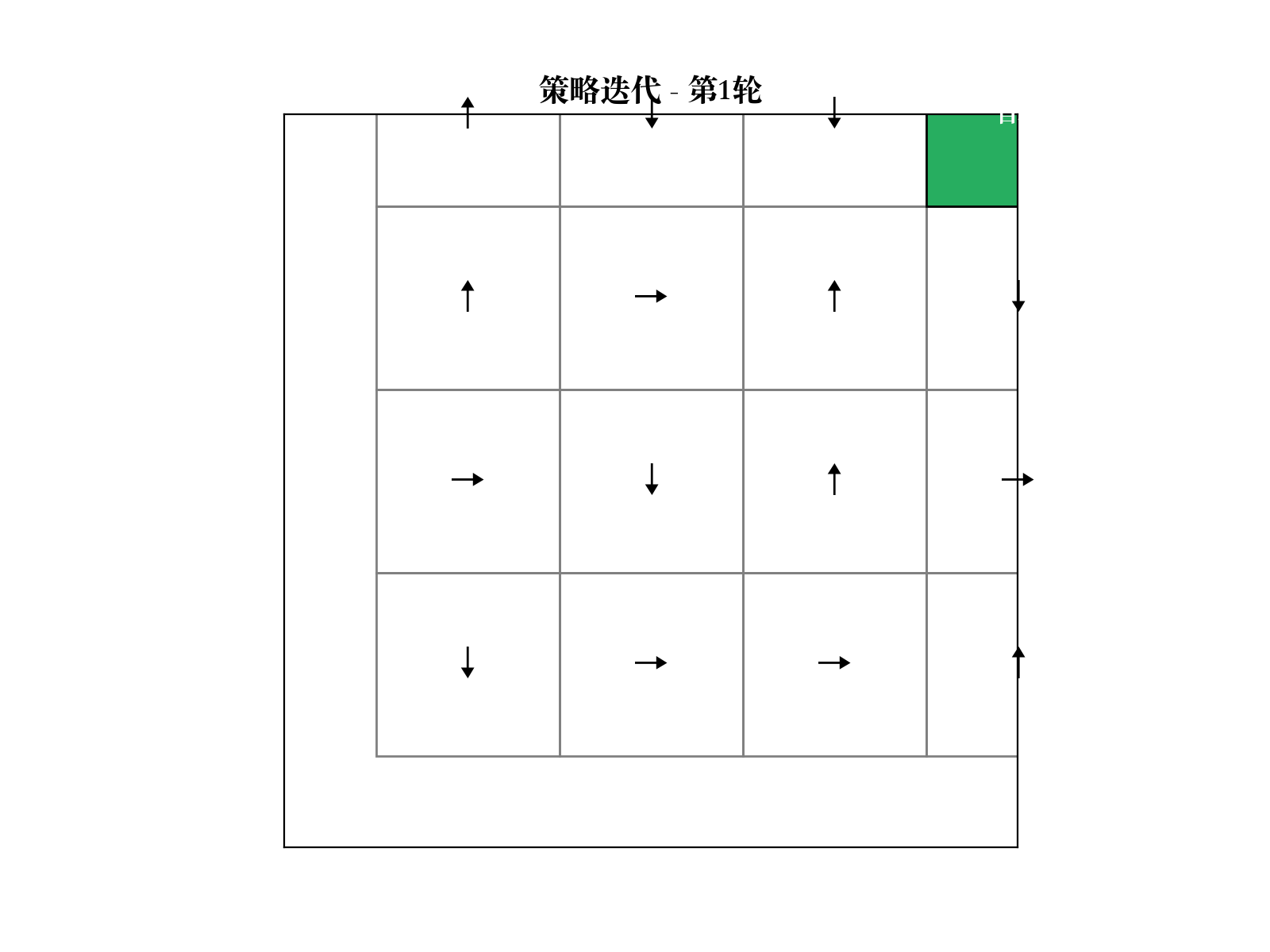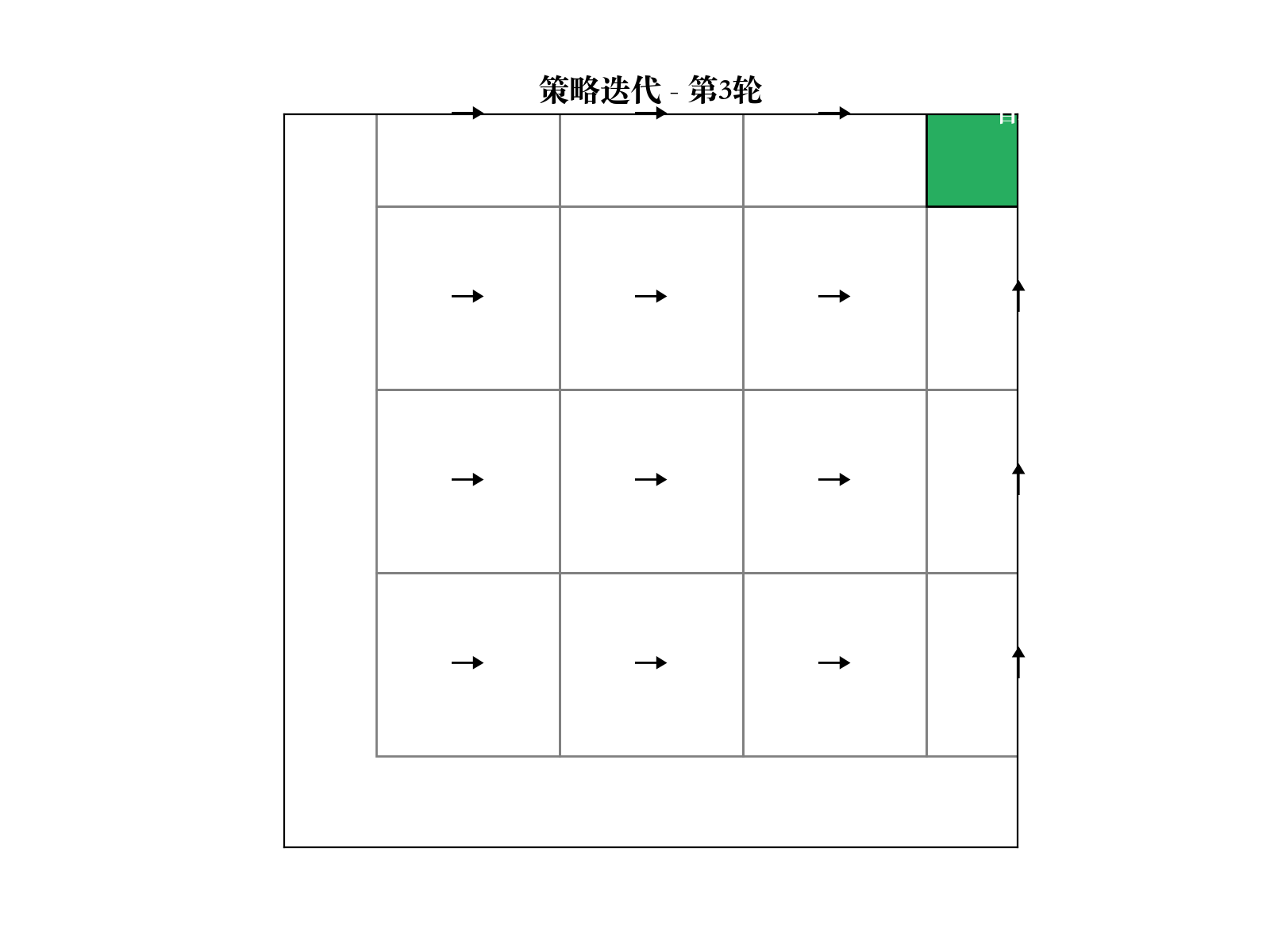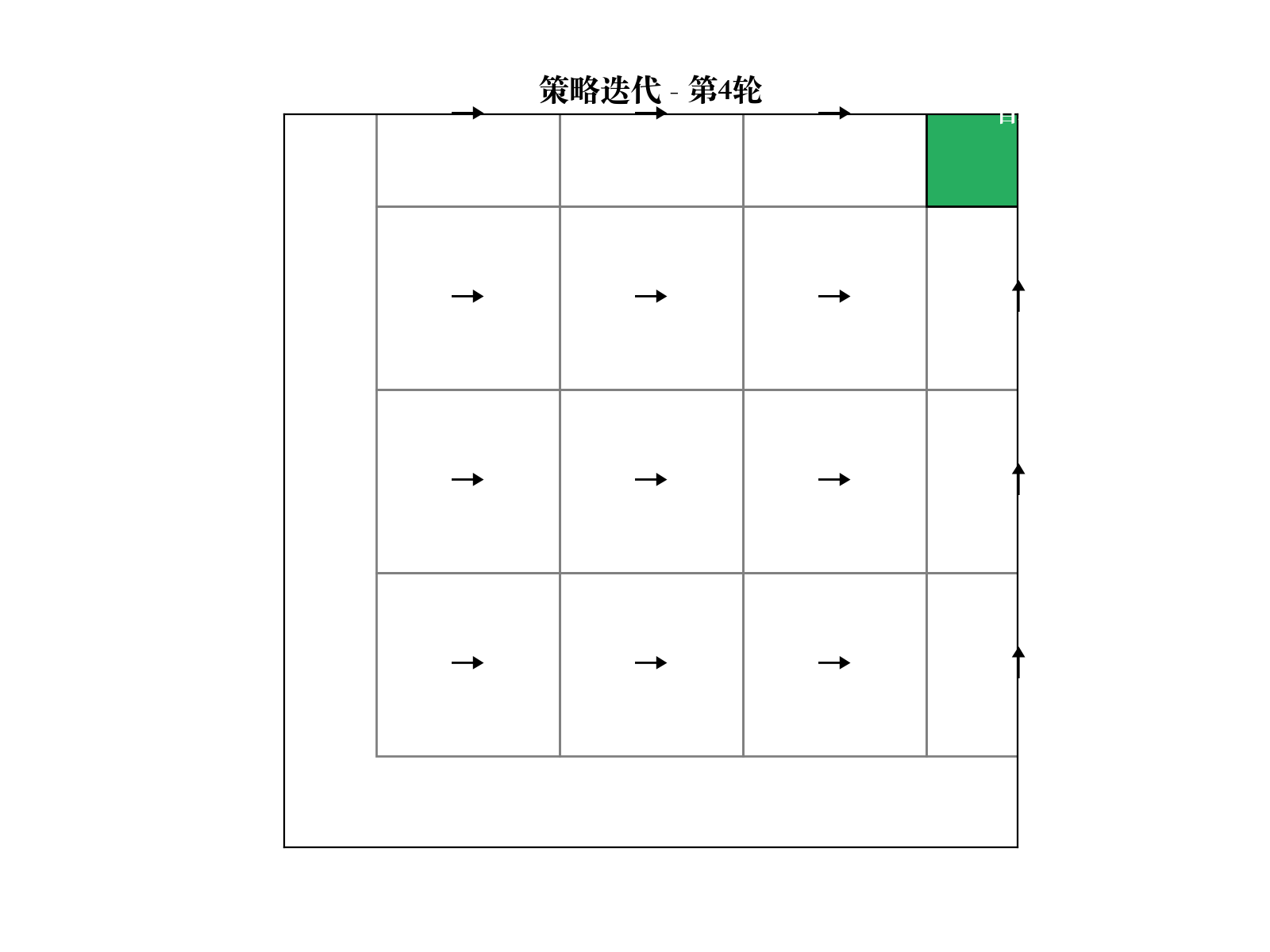
值迭代算法

直接迭代最优 Bellman 方程：

1. 初始化 2. 重复直到收敛：

$$

V_{k+1}(s) {a A} {s' S} P(s'|s, a) $$3. 提取最优策略：

值迭代实际上是策略迭代的简化版本：每次迭代隐式地进行了一次策略评估和改进。

收敛性：

定义 Bellman 算子 ：

可以证明 是 -收缩映射：

因此值迭代以指数速度收敛到唯一不动点 。

代码实现： GridWorld 环境

实现一个简单的网格世界，智能体从起点移动到终点，撞墙会停在原地。

import numpy as np
import matplotlib.pyplot as plt
from typing import Tuple, List

class GridWorld:
    """
    简单的网格世界环境
    
    参数：
        grid_size: (height, width)，网格大小
        start: (row, col)，起点位置
        goal: (row, col)，终点位置
        obstacles: List[(row, col)]，障碍物位置
    """
    def __init__(self, grid_size=(5, 5), start=(0, 0), goal=(4, 4), obstacles=[]):
        self.height, self.width = grid_size
        self.start = start
        self.goal = goal
        self.obstacles = set(obstacles)
        
        # 动作空间： 0=上, 1=下, 2=左, 3=右
        self.actions = [0, 1, 2, 3]
        self.action_names = ['↑', '↓', '←', '→']
        
        # 动作对应的状态变化
        self.action_deltas = {
            0: (-1, 0),  # 上
            1: (1, 0),   # 下
            2: (0, -1),  # 左
            3: (0, 1)    # 右
        }
        
        self.reset()
    
    def reset(self) -> Tuple[int, int]:
        """重置环境，返回起点"""
        self.state = self.start
        return self.state
    
    def step(self, action: int) -> Tuple[Tuple[int, int], float, bool]:
        """
        执行动作
        
        返回：
            next_state: 下一状态
            reward: 即时奖励
            done: 是否到达终点
        """
        dr, dc = self.action_deltas[action]
        next_r = self.state[0] + dr
        next_c = self.state[1] + dc
        
        # 检查边界和障碍物
        if (0 <= next_r < self.height and 0 <= next_c < self.width and
            (next_r, next_c) not in self.obstacles):
            self.state = (next_r, next_c)
        
        # 奖励：到达终点+10，其他-1
        if self.state == self.goal:
            return self.state, 10.0, True
        else:
            return self.state, -1.0, False
    
    def get_transition_prob(self, state, action):
        """
        获取转移概率（确定性环境）
        
        返回：
            List[(next_state, prob, reward)]
        """
        # 保存当前状态
        old_state = self.state
        self.state = state
        
        # 执行动作
        next_state, reward, done = self.step(action)
        
        # 恢复状态
        self.state = old_state
        
        return [(next_state, 1.0, reward)]

def value_iteration(env: GridWorld, gamma=0.9, theta=1e-6, max_iter=1000):
    """
    值迭代算法
    
    参数：
        env: 环境对象
        gamma: 折扣因子
        theta: 收敛阈值
        max_iter: 最大迭代次数
    
    返回：
        V: 状态价值函数， shape=(height, width)
        policy: 最优策略， shape=(height, width)
    """
    height, width = env.height, env.width
    V = np.zeros((height, width))
    
    for iter_count in range(max_iter):
        delta = 0
        
        # 遍历所有状态
        for r in range(height):
            for c in range(width):
                state = (r, c)
                
                # 跳过终点和障碍物
                if state == env.goal or state in env.obstacles:
                    continue
                
                v = V[r, c]
                
                # 计算所有动作的 Q 值
                q_values = []
                for action in env.actions:
                    q = 0
                    transitions = env.get_transition_prob(state, action)
                    for next_state, prob, reward in transitions:
                        next_r, next_c = next_state
                        q += prob * (reward + gamma * V[next_r, next_c])
                    q_values.append(q)
                
                # Bellman 最优更新
                V[r, c] = max(q_values)
                delta = max(delta, abs(v - V[r, c]))
        
        # 检查收敛
        if delta < theta:
            print(f"值迭代在第 {iter_count + 1} 次迭代后收敛")
            break
    
    # 提取最优策略
    policy = np.zeros((height, width), dtype=int)
    for r in range(height):
        for c in range(width):
            state = (r, c)
            if state == env.goal or state in env.obstacles:
                continue
            
            q_values = []
            for action in env.actions:
                q = 0
                transitions = env.get_transition_prob(state, action)
                for next_state, prob, reward in transitions:
                    next_r, next_c = next_state
                    q += prob * (reward + gamma * V[next_r, next_c])
                q_values.append(q)
            
            policy[r, c] = np.argmax(q_values)
    
    return V, policy

def visualize_policy(env: GridWorld, V, policy):
    """可视化价值函数和策略"""
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
    
    # 价值函数热力图
    im1 = ax1.imshow(V, cmap='coolwarm')
    ax1.set_title('State Value Function V(s)')
    plt.colorbar(im1, ax=ax1)
    
    # 标注数值
    for r in range(env.height):
        for c in range(env.width):
            if (r, c) == env.goal:
                ax1.text(c, r, 'G', ha='center', va='center', color='white', fontsize=16, fontweight='bold')
            elif (r, c) in env.obstacles:
                ax1.text(c, r, 'X', ha='center', va='center', color='black', fontsize=16)
            else:
                ax1.text(c, r, f'{V[r, c]:.1f}', ha='center', va='center')
    
    # 策略箭头
    ax2.imshow(np.zeros((env.height, env.width)), cmap='gray', alpha=0.3)
    ax2.set_title('Optimal Policy π*(s)')
    
    for r in range(env.height):
        for c in range(env.width):
            if (r, c) == env.goal:
                ax2.text(c, r, 'G', ha='center', va='center', color='green', fontsize=16, fontweight='bold')
            elif (r, c) in env.obstacles:
                ax2.text(c, r, 'X', ha='center', va='center', color='red', fontsize=16)
            else:
                action = policy[r, c]
                ax2.text(c, r, env.action_names[action], ha='center', va='center', fontsize=20)
    
    plt.tight_layout()
    plt.savefig('gridworld_value_iteration.png', dpi=150)
    plt.show()

# 运行示例
if __name__ == "__main__":
    # 创建 5x5 网格世界，设置障碍物
    env = GridWorld(
        grid_size=(5, 5),
        start=(0, 0),
        goal=(4, 4),
        obstacles=[(1, 1), (2, 2), (3, 1)]
    )
    
    # 运行值迭代
    V, policy = value_iteration(env, gamma=0.9, theta=1e-6)
    
    # 可视化结果
    visualize_policy(env, V, policy)
    
    print("\n 最优价值函数：")
    print(V)
    print("\n 最优策略：")
    for r in range(env.height):
        for c in range(env.width):
            if (r, c) == env.goal:
                print('G', end=' ')
            elif (r, c) in env.obstacles:
                print('X', end=' ')
            else:
                print(env.action_names[policy[r, c]], end=' ')
        print()

代码解读：

1. 类实现环境，提供状态转移和奖励
2. 实现值迭代算法，直到价值函数收敛（）
3. 最优策略通过贪婪选择 提取
4. 可视化展示价值函数的热力图和策略的方向箭头

蒙特卡洛方法：无需模型的学习

动态规划需要完整的环境模型，但实际中环境模型往往未知或难以建模。蒙特卡洛（ Monte Carlo, MC）方法通过采样轨迹来估计价值函数，无需环境模型。

核心思想

MC 方法的基本思路：价值函数是期望回报，可以用样本均值近似：

$$

V^(s) = {i=1}^N G_t^{(i)} $$

其中 是第 次从状态 开始的轨迹中观察到的回报。

步骤：

1. 智能体按策略 与环境交互，生成完整的轨迹（ episode）：

$$

S_0, A_0, R_1, S_1, A_1, R_2, , S_T $$2. 对轨迹中的每个状态 ，计算从该状态开始的回报 3. 更新 为所有访问 时观察到的回报的平均值

First-Visit MC vs Every-Visit MC

First-Visit MC：

对每条轨迹，只在第一次访问状态 时记录回报。

算法：

1. 初始化 ，（空列表）
2. 对每条轨迹：
   • 计算每个时刻的回报 - 对每个状态 （仅第一次出现）：
     • 将 加入 - Every-Visit MC：

对每条轨迹，每次访问状态 都记录回报。

两者的区别在于对同一轨迹中多次访问同一状态的处理。 First-Visit MC 更常用，且其无偏性易证明。

MC 策略评估的收敛性

定理： First-Visit MC 方法收敛到真实价值函数：

$$

V_N(s) V^(s) $$

其中 是访问状态 的轨迹数。

证明：每次访问 观察到的回报 是独立同分布的随机变量，其期望为 。根据大数定律，样本均值收敛到期望。

MC 控制：策略改进

MC 方法也可以用于控制问题（寻找最优策略）。关键是估计 而非 ，因为策略改进需要知道每个动作的价值。

MC 控制算法（基于 exploring starts）：

1. 初始化策略 和 2. 重复：
   • 生成轨迹：从随机状态-动作对开始，按策略 采样
   • 策略评估：对轨迹中每个 对，更新 为观察到的回报均值
   • 策略改进：对每个 ，更新 Exploring Starts 假设：

每个状态-动作对都有非零概率作为起点。这保证了所有状态-动作对都能被访问到。

ε-贪婪策略：平衡探索与利用

Exploring Starts 在实际中难以实现。更实用的方法是使用 -贪婪策略：

以概率 选择当前最优动作（利用），以概率 随机选择动作（探索）。

On-Policy vs Off-Policy：

• On-Policy：评估和改进的是当前执行的策略（如 -贪婪）
• Off-Policy：评估一个策略（目标策略 ），但执行另一个策略（行为策略 ）

MC 控制通常是 On-Policy 的。

增量式更新

存储所有回报并计算平均值的空间开销大。增量式更新公式：

$$

V(s) V(s) + $$

其中 是学习率。这是加权平均，近期样本权重更大（当 为常数时）。

代码实现： MC 策略评估

import numpy as np
from collections import defaultdict

def mc_policy_evaluation(env, policy, num_episodes=10000, gamma=0.9):
    """
    蒙特卡洛策略评估（ First-Visit）
    
    参数：
        env: 环境对象
        policy: 策略函数， policy(state) -> action
        num_episodes: 采样轨迹数
        gamma: 折扣因子
    
    返回：
        V: 状态价值函数字典
    """
    # 存储每个状态的回报列表
    returns = defaultdict(list)
    V = defaultdict(float)
    
    for episode in range(num_episodes):
        # 生成一条轨迹
        trajectory = []
        state = env.reset()
        done = False
        
        while not done:
            action = policy(state)
            next_state, reward, done = env.step(action)
            trajectory.append((state, action, reward))
            state = next_state
        
        # 计算回报（从后向前）
        G = 0
        visited_states = set()
        
        for t in range(len(trajectory) - 1, -1, -1):
            state, action, reward = trajectory[t]
            G = reward + gamma * G
            
            # First-Visit：只在第一次访问时记录
            if state not in visited_states:
                visited_states.add(state)
                returns[state].append(G)
                V[state] = np.mean(returns[state])
        
        if (episode + 1) % 1000 == 0:
            print(f"完成 {episode + 1} 条轨迹")
    
    return V

def mc_control(env, num_episodes=10000, gamma=0.9, epsilon=0.1):
    """
    蒙特卡洛控制（ On-Policy, ε-贪婪）
    
    返回：
        Q: 动作价值函数字典
        policy: 学到的策略
    """
    Q = defaultdict(lambda: np.zeros(len(env.actions)))
    returns = defaultdict(list)
    
    for episode in range(num_episodes):
        # 生成轨迹（使用ε-贪婪策略）
        trajectory = []
        state = env.reset()
        done = False
        
        while not done:
            # ε-贪婪选择动作
            if np.random.random() < epsilon:
                action = np.random.choice(env.actions)
            else:
                action = np.argmax(Q[state])
            
            next_state, reward, done = env.step(action)
            trajectory.append((state, action, reward))
            state = next_state
        
        # 更新 Q 值
        G = 0
        visited_sa = set()
        
        for t in range(len(trajectory) - 1, -1, -1):
            state, action, reward = trajectory[t]
            G = reward + gamma * G
            
            if (state, action) not in visited_sa:
                visited_sa.add((state, action))
                returns[(state, action)].append(G)
                Q[state][action] = np.mean(returns[(state, action)])
        
        if (episode + 1) % 1000 == 0:
            print(f"完成 {episode + 1} 条轨迹")
    
    # 提取贪婪策略
    policy = lambda s: np.argmax(Q[s])
    
    return Q, policy

MC 方法的优缺点：

优点： - 无需环境模型 - 可以从实际经验或模拟中学习 - 可以专注于感兴趣的状态 - 简单、直观

缺点： - 需要完整的轨迹（必须等到 episode 结束） - 高方差（回报是多个随机奖励的和） - 在连续任务或长 episode 中效率低

时序差分学习：结合 MC 和 DP 的优点

时序差分（ Temporal Difference, TD）学习是强化学习的核心，结合了 MC 的无模型特性和 DP 的 bootstrapping 。

TD(0)：最简单的 TD 方法

TD(0)的更新规则：

$$

V(S_t) V(S_t) + $$

TD 误差：

TD 误差衡量"实际观察（）"与"当前估计（）"之间的差异。

与 MC 的对比：

方法	更新目标	特点
MC	（实际回报）	无偏，高方差，需要完整轨迹
TD(0)	（ bootstrapped 估计）	有偏（初期），低方差，单步更新

TD 方法在每一步之后就可以更新，无需等待 episode 结束。这使得 TD 方法可以用于连续任务（没有明确结束状态的任务）。

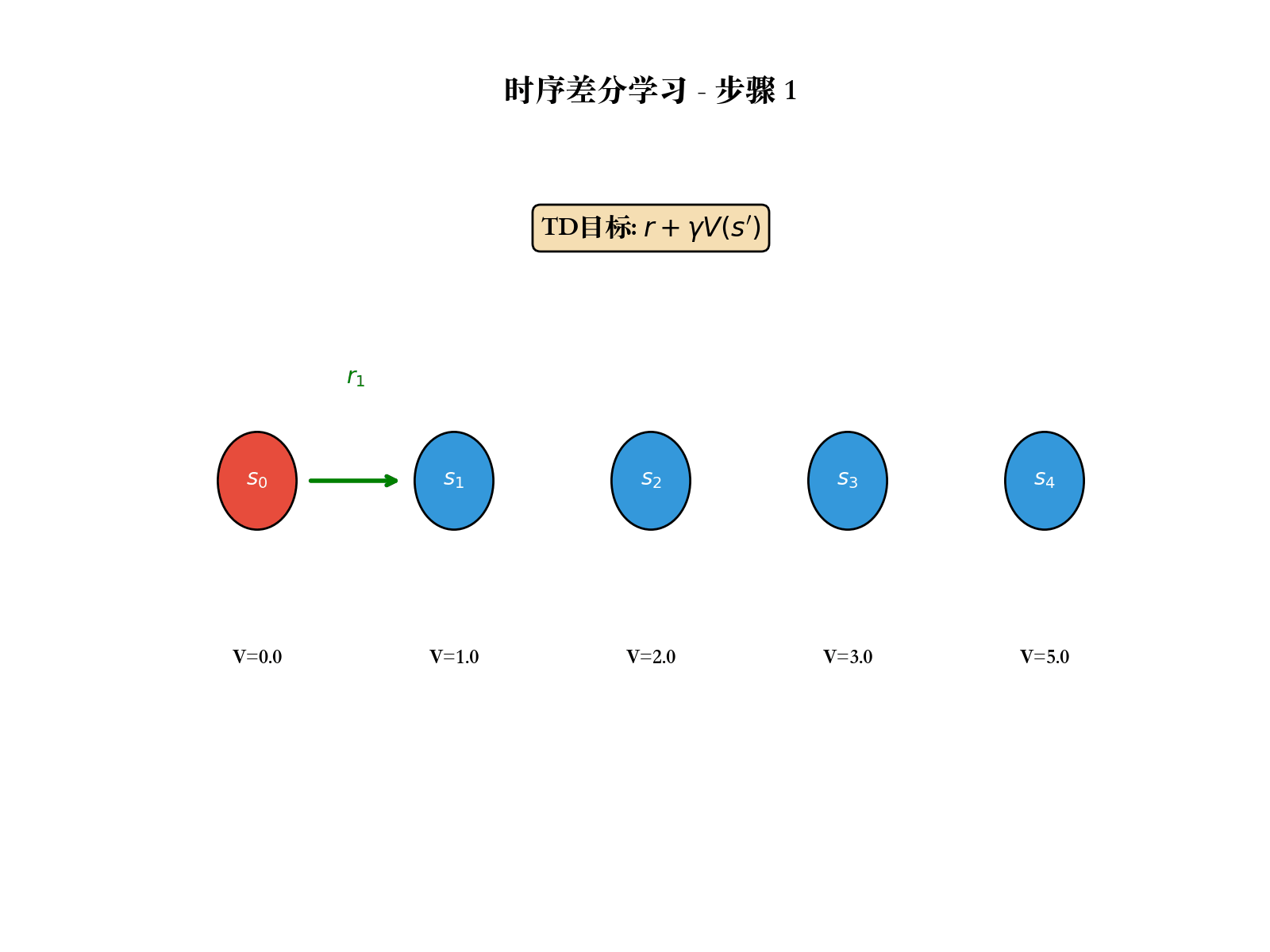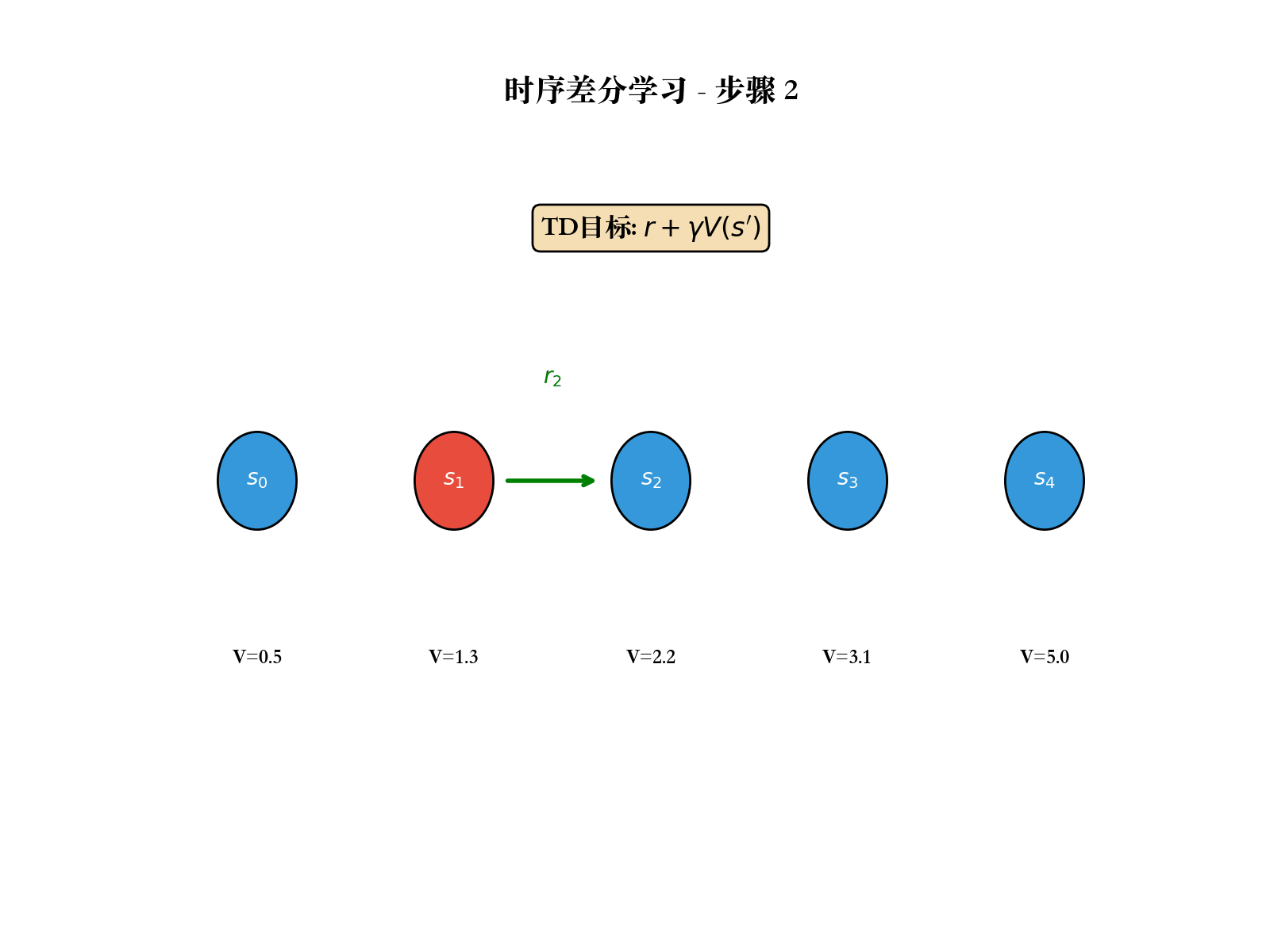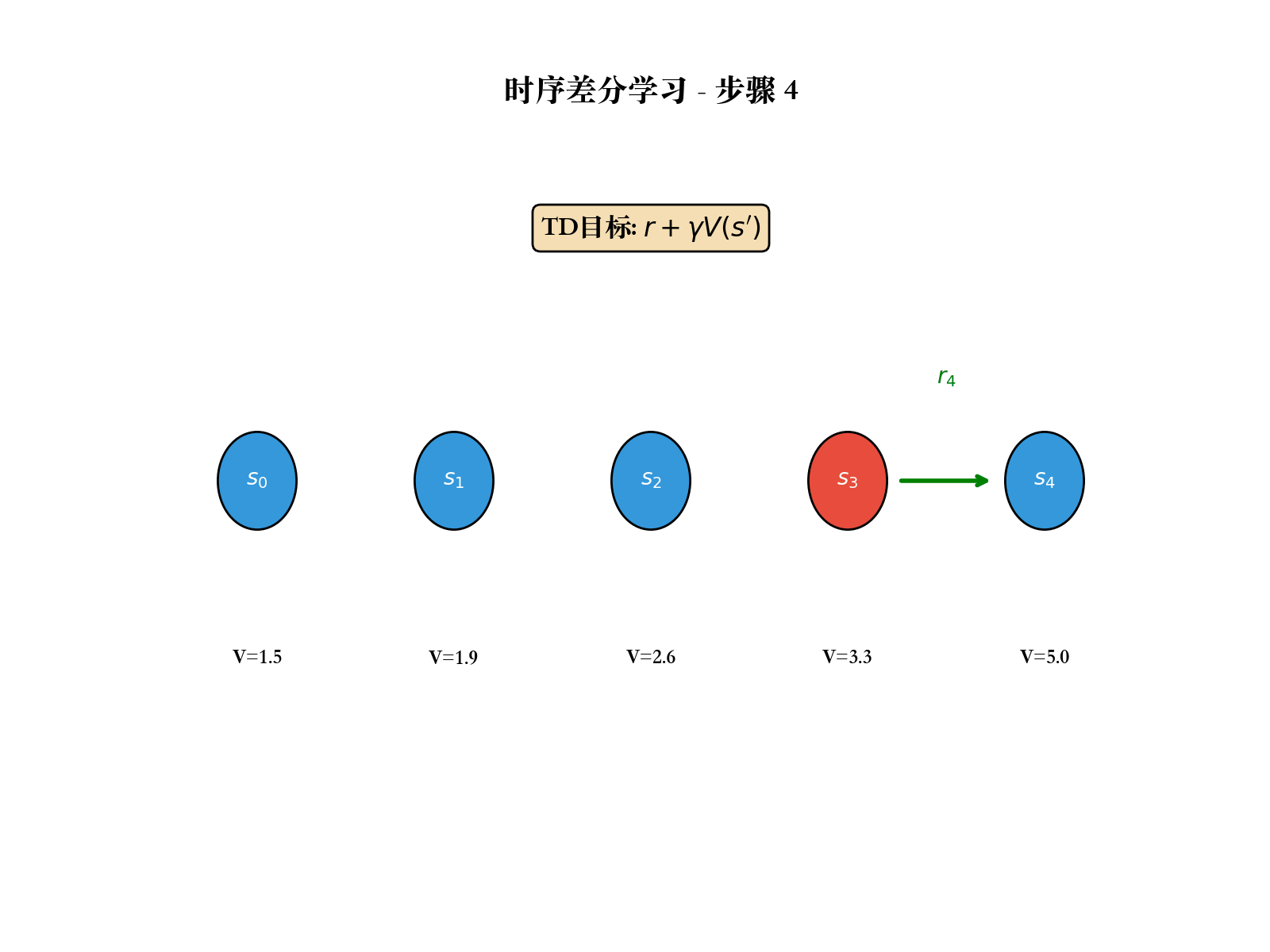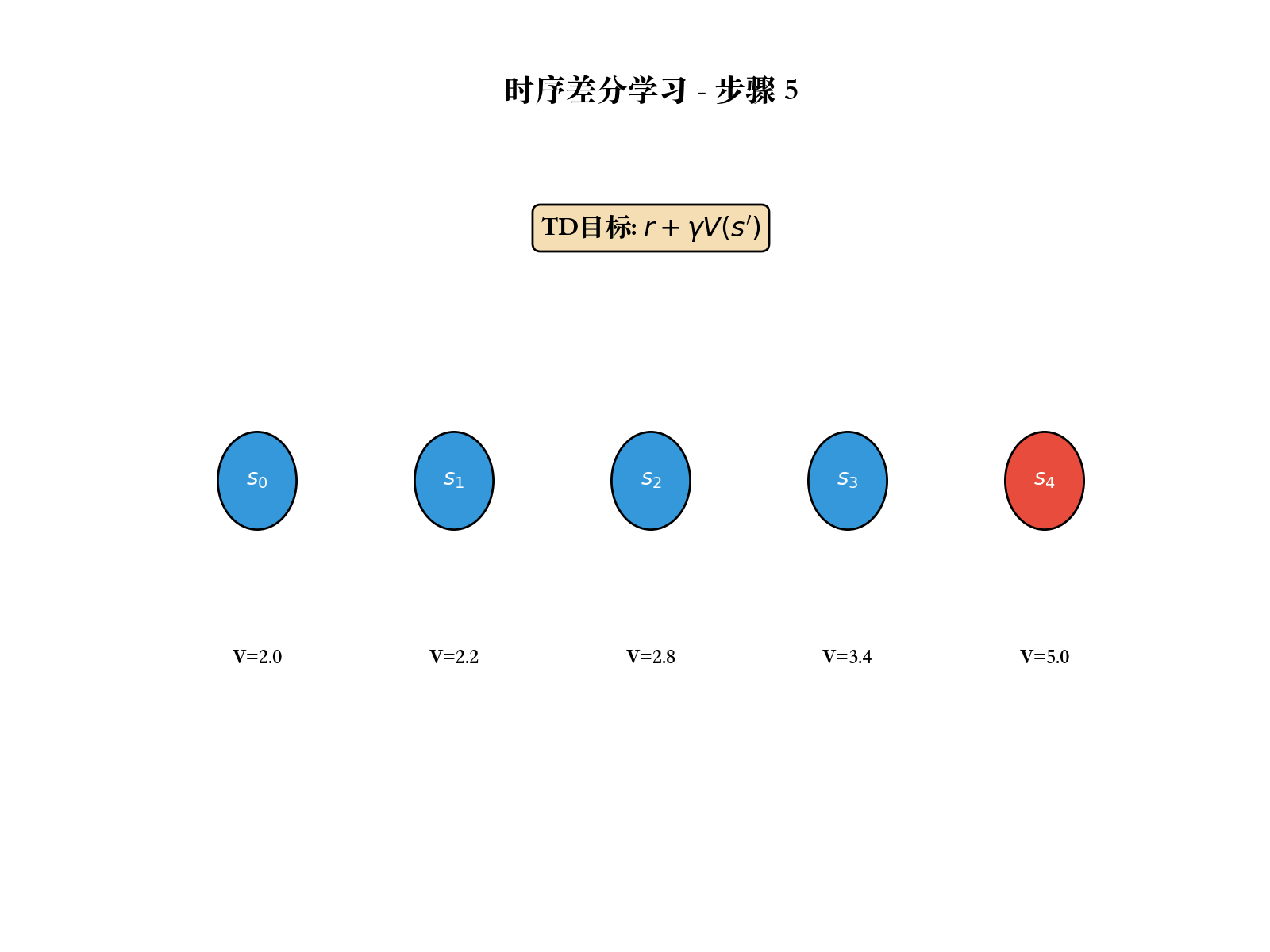
TD(0)的收敛性

定理（ Sutton, 1988）：对于任意策略 ，如果满足：

1. 学习率满足 Robbins-Monro 条件：2. 所有状态-动作对被无限次访问

则 TD(0)几乎必然收敛到 。

常用的学习率： 或固定小值（如 0.1）。

Sarsa： On-Policy TD 控制

Sarsa（ State-Action-Reward-State-Action）是 Q 函数的 TD 版本：

$$

Q(S_t, A_t) Q(S_t, A_t) + $$

算法名称来源于更新所需的五元组：。

Sarsa 算法：

1. 初始化 2. 对每个 episode：
   • 初始化 - 根据 选择动作 （如 -贪婪）
   • 重复（对 episode 中的每一步）：
     • 执行 ，观察 - 根据 从 选择 - 更新： - - 直到 是终止状态

Sarsa 是 On-Policy 方法：评估和改进的是当前执行的策略（如 -贪婪）。

Q-Learning： Off-Policy TD 控制

Q-Learning 是 TD 方法中最重要的突破之一（ Watkins, 1989）。

Q-Learning 更新规则：

$$

Q(S_t, A_t) Q(S_t, A_t) + $$

与 Sarsa 的区别在于： Sarsa 使用实际执行的下一个动作 ， Q-Learning 使用最优动作 。

Q-Learning 算法：

1. 初始化 2. 对每个 episode：
   • 初始化 - 重复（对 episode 中的每一步）：
     • 根据 选择动作 （如 -贪婪）
     • 执行 ，观察 - 更新： - - 直到 是终止状态

Q-Learning 是 Off-Policy 方法：行为策略（如 -贪婪）用于探索，目标策略（贪婪策略）用于评估。

Q-Learning 的收敛性：

定理（ Watkins & Dayan, 1992）：如果：

1. 所有状态-动作对被无限次访问
2. 学习率满足 Robbins-Monro 条件

则 Q-Learning 收敛到最优 Q 函数 ，与行为策略无关。

这是 Q-Learning 的巨大优势：可以从任意策略产生的数据中学习最优策略。

Sarsa vs Q-Learning：直觉对比

考虑"悬崖行走"环境：

S: 起点, G: 终点, C: 悬崖（ reward=-100）

S . . . . . . G
C C C C C C C C

智能体从起点到终点，掉入悬崖会回到起点并获得大负奖励。

Sarsa（ On-Policy）：

由于使用 -贪婪策略， Sarsa 会考虑到探索时可能掉入悬崖。它学到的策略会远离悬崖边缘，走更安全但更长的路径。

Q-Learning（ Off-Policy）：

Q-Learning 评估的是贪婪策略，假设不会随机探索。它学到的策略会沿着悬崖边缘走最短路径，但在执行时（由于 -贪婪）可能掉入悬崖。

这说明： - Sarsa 更保守（考虑了探索的风险） - Q-Learning 更激进（评估的是最优策略）

TD(λ)与资格迹

TD(0)只使用一步的奖励进行 bootstrapping 。 TD()是更一般的框架，结合了多步回报。

-步回报：

$$

G_t^{(n)} = R_{t+1} + R_{t+2} + + ^{n-1} R_{t+n} + ^n V(S_{t+n}) $$

TD()更新：

使用所有 -步回报的加权平均：

$$

G_t^= (1 - ) _{n=1}^{} ^{n-1} G_t^{(n)} $$

其中 控制权重分配。

资格迹（ Eligibility Trace）：

资格迹是一种高效的实现方式，为每个状态维护一个迹 ：

$$

e_t(s) =

$$

更新规则：

$$

V(s) V(s) + _t e_t(s), s $$

资格迹记录了状态的"功劳"：最近访问的状态和频繁访问的状态有更高的迹，获得更多的信用分配。

特殊情况：

• : TD(0)
• : 等价于 MC（使用完整回报）

代码实现： Sarsa 和 Q-Learning

import numpy as np

def sarsa(env, num_episodes=1000, alpha=0.1, gamma=0.9, epsilon=0.1):
    """
    Sarsa 算法（ On-Policy TD 控制）
    
    参数：
        env: 环境对象
        num_episodes: 训练轮数
        alpha: 学习率
        gamma: 折扣因子
        epsilon: 探索率
    
    返回：
        Q: 学到的 Q 函数
    """
    # 初始化 Q 表
    Q = {}
    for r in range(env.height):
        for c in range(env.width):
            Q[(r, c)] = np.zeros(len(env.actions))
    
    for episode in range(num_episodes):
        state = env.reset()
        
        # 选择初始动作（ε-贪婪）
        if np.random.random() < epsilon:
            action = np.random.choice(env.actions)
        else:
            action = np.argmax(Q[state])
        
        done = False
        
        while not done:
            # 执行动作
            next_state, reward, done = env.step(action)
            
            # 选择下一个动作（ε-贪婪）
            if np.random.random() < epsilon:
                next_action = np.random.choice(env.actions)
            else:
                next_action = np.argmax(Q[next_state])
            
            # Sarsa 更新：使用实际执行的 next_action
            td_target = reward + gamma * Q[next_state][next_action]
            td_error = td_target - Q[state][action]
            Q[state][action] += alpha * td_error
            
            # 转移
            state = next_state
            action = next_action
        
        if (episode + 1) % 100 == 0:
            print(f"Sarsa 完成第 {episode + 1} 轮")
    
    return Q

def q_learning(env, num_episodes=1000, alpha=0.1, gamma=0.9, epsilon=0.1):
    """
    Q-Learning 算法（ Off-Policy TD 控制）
    
    返回：
        Q: 学到的 Q 函数
    """
    # 初始化 Q 表
    Q = {}
    for r in range(env.height):
        for c in range(env.width):
            Q[(r, c)] = np.zeros(len(env.actions))
    
    for episode in range(num_episodes):
        state = env.reset()
        done = False
        
        while not done:
            # 选择动作（ε-贪婪）
            if np.random.random() < epsilon:
                action = np.random.choice(env.actions)
            else:
                action = np.argmax(Q[state])
            
            # 执行动作
            next_state, reward, done = env.step(action)
            
            # Q-Learning 更新：使用 max_a Q(s', a)
            td_target = reward + gamma * np.max(Q[next_state])
            td_error = td_target - Q[state][action]
            Q[state][action] += alpha * td_error
            
            # 转移
            state = next_state
        
        if (episode + 1) % 100 == 0:
            print(f"Q-Learning 完成第 {episode + 1} 轮")
    
    return Q

def sarsa_lambda(env, num_episodes=1000, alpha=0.1, gamma=0.9, epsilon=0.1, lambda_=0.9):
    """
    Sarsa(λ) 算法（带资格迹）
    
    参数：
        lambda_: 资格迹衰减因子
    """
    Q = {}
    for r in range(env.height):
        for c in range(env.width):
            Q[(r, c)] = np.zeros(len(env.actions))
    
    for episode in range(num_episodes):
        # 初始化资格迹
        E = {}
        for r in range(env.height):
            for c in range(env.width):
                E[(r, c)] = np.zeros(len(env.actions))
        
        state = env.reset()
        
        # 选择初始动作
        if np.random.random() < epsilon:
            action = np.random.choice(env.actions)
        else:
            action = np.argmax(Q[state])
        
        done = False
        
        while not done:
            # 执行动作
            next_state, reward, done = env.step(action)
            
            # 选择下一个动作
            if np.random.random() < epsilon:
                next_action = np.random.choice(env.actions)
            else:
                next_action = np.argmax(Q[next_state])
            
            # 计算 TD 误差
            td_error = reward + gamma * Q[next_state][next_action] - Q[state][action]
            
            # 更新资格迹（当前状态-动作对）
            E[state][action] += 1
            
            # 更新所有状态-动作对
            for s in E:
                for a in range(len(env.actions)):
                    Q[s][a] += alpha * td_error * E[s][a]
                    E[s][a] *= gamma * lambda_
            
            # 转移
            state = next_state
            action = next_action
        
        if (episode + 1) % 100 == 0:
            print(f"Sarsa(λ)完成第 {episode + 1} 轮")
    
    return Q

# 对比实验
if __name__ == "__main__":
    from gridworld import GridWorld
    
    env = GridWorld(grid_size=(5, 5), start=(0, 0), goal=(4, 4), obstacles=[(2, 2)])
    
    print("训练 Sarsa...")
    Q_sarsa = sarsa(env, num_episodes=1000)
    
    print("\n 训练 Q-Learning...")
    Q_qlearn = q_learning(env, num_episodes=1000)
    
    print("\n 训练 Sarsa(λ)...")
    Q_sarsa_lambda = sarsa_lambda(env, num_episodes=1000, lambda_=0.9)
    
    # 提取策略并对比
    policy_sarsa = {s: np.argmax(Q_sarsa[s]) for s in Q_sarsa}
    policy_qlearn = {s: np.argmax(Q_qlearn[s]) for s in Q_qlearn}
    
    print("\n 策略对比完成")

代码要点：

1. Sarsa 使用 更新，其中 是实际执行的动作
2. Q-Learning 使用 更新，取 $a Q(S{t+1}, a)$) 维护资格迹矩阵 ，为每个状态-动作对记录"功劳"
3. 三种方法都使用 -贪婪进行探索

❓ Q&A：强化学习基础常见疑问

Q1：为什么需要折扣因子 ？能否直接最大化无折扣的回报？

数学必要性：

在无限时间步的任务中，无折扣回报 可能发散到无穷大。折扣因子保证了回报有界：

$$

G = {t=0}t R_t {t=0}t R_{} = {1 - } $$

经济学解释：

折扣因子反映了"时间价值"：今天的 1 元比明天的 1 元更值钱。在强化学习中，这体现为：

• 早期获得的奖励更有价值（减少不确定性）
• 避免智能体无限期延迟获取奖励

实践影响：

取值	行为特征	适用场景
0.0 - 0.5	短视（ myopic），只关注近期奖励	金融交易、快速决策
0.9 - 0.95	平衡，常用默认值	大多数任务
0.99 - 0.999	远视，重视长期收益	围棋、战略规划
1.0	无折扣（仅用于有限步任务）	有明确终止的游戏

选择建议：

• 如果任务有明确终止状态（ episodic）， 可以接近 1
• 如果任务是连续的， 应该 < 1

• 通过交叉验证调优

Q2： Bellman 方程为什么是"收缩映射"？这对收敛性有什么影响？

收缩映射定义：

算子 是收缩映射，如果存在 使得对任意函数 ：

其中 。

Bellman 算子的收缩性证明：

定义 Bellman 算子：

证明：

Banach 不动点定理：

收缩映射有唯一不动点，且任意初值的迭代序列都收敛到该不动点：

$$

V_{k+1} = TV_k V_k V^{*} $$

收敛速度：

指数收敛！这意味着值迭代和策略评估都能快速收敛。

实践意义：

• 越小，收敛越快（但策略质量可能下降）
• 可以用 作为停止条件
• 即使初始值很差，也能保证收敛到最优值

---

Q3：动态规划需要完整的模型，但实际中模型往往未知。这是否意味着 DP 没有实用价值？

模型可获得的情况：

1. 游戏规则已知：棋类游戏（围棋、国际象棋）、电子游戏
2. 仿真环境：机器人仿真器（ MuJoCo 、 Gazebo）、自动驾驶仿真
3. 学习模型：使用监督学习从数据中学习转移函数 和奖励 Model-Based RL：

结合模型学习和规划：

1. 从真实交互中收集数据 2. 学习模型 和 3. 在学习的模型上用 DP 规划

这称为 Dyna 架构（ Sutton, 1990）。

DP 的理论价值：

即使不直接使用 DP 算法，其理论框架（ Bellman 方程、策略改进定理）是所有 RL 方法的基础：

• TD 方法本质上是 DP 的采样版本
• 策略梯度方法的收敛性依赖于策略改进定理
• 深度 RL 中的目标网络源于 DP 的思想

实用建议：

• 如果模型已知或容易建模，优先用 DP（最高效）
• 如果模型未知但可以采样，用 MC 或 TD
• 如果样本昂贵，考虑 model-based 方法

---

Q4：蒙特卡洛方法和 TD 方法哪个更好？

两者各有优劣，取决于任务特性：

蒙特卡洛方法：

✅ 优点： - 无偏估计（期望回报的样本均值收敛到真实值） - 不依赖 Markov 性质 - 简单直观

❌ 缺点： - 高方差（回报是长序列随机奖励的和） - 需要完整轨迹（不能用于连续任务） - 学习慢（尤其是长轨迹）

TD 方法：

✅ 优点： - 低方差（只依赖一步的随机性） - 单步更新（可用于连续任务） - 学习快（充分利用 bootstrapping）

❌ 缺点： - 有偏（初始时基于不准确的估计） - 依赖 Markov 性质 - 对初始值敏感

经验法则：

任务特征	推荐方法	理由
短 episode	MC	方差不大，无偏估计更重要
长/连续任务	TD	必须单步更新
高随机性	TD	MC 方差太大
函数逼近	TD	MC 的高方差会放大逼近误差
离线数据	MC	固定轨迹，无法 bootstrapping

组合使用：

TD() 通过参数 在 MC 和 TD 之间插值：

• : TD(0)
• : 接近 MC
• : 平衡偏差和方差

实践中 通常效果最好。

---

Q5： Q-Learning 保证收敛到最优策略，为什么还需要 Sarsa？

Q-Learning 确实有更强的理论保证（收敛到 ），但 Sarsa 在某些场景下更实用：

安全性考虑：

Sarsa 是 On-Policy 方法，评估的是实际执行的策略（包括探索）。在安全敏感的任务中（如机器人控制、医疗决策）， Sarsa 学到的策略会更保守。

示例（悬崖行走）：

起点 ← ← ← ← ← ← ← 终点
悬崖悬崖悬崖悬崖悬崖悬崖悬崖悬崖

• Q-Learning：学到沿悬崖边缘的最短路径（评估贪婪策略），但执行时会频繁掉入悬崖（因为 -探索）
• Sarsa：学到远离悬崖的安全路径（考虑了探索的风险）

探索策略的影响：

Q-Learning 的收敛性要求所有状态-动作对被无限次访问，但不要求特定的探索策略。 Sarsa 的性能直接依赖于探索策略的质量。

收敛速度：

理论上 Q-Learning 收敛更快（直接优化最优策略），但实践中：

• 如果探索策略与最优策略差异大， Q-Learning 的样本效率可能更低
• Sarsa 在某些任务上收敛更稳定

实用建议：

• 优先尝试 Q-Learning：更通用，理论更强
• 如果出现以下情况，改用 Sarsa：
  • 训练不稳定
  • 任务有安全要求
  • 探索噪声大

---

Q6：为什么资格迹能加速信用分配？

信用分配问题：在长轨迹中，早期的动作如何获得远期奖励的"功劳"？

TD(0)的局限：

TD(0)只回传一步：

$$

V(S_t) V(S_t) + $$

如果在时刻 获得奖励，只有 被直接更新。需要经过多次迭代才能间接受益。

资格迹的机制：

资格迹 记录状态 对当前奖励的"责任"：

$$

e_t(s) =

$$

更新规则：

$$

V(s) V(s) + _t e_t(s), s $$

直觉：

• 频率启发：频繁访问的状态有更高的迹（累积效应）
• 时效性启发：最近访问的状态有更高的迹（衰减 ）
• 全局更新：每个 TD 误差 更新所有状态（根据其资格迹权重）

示例：

假设轨迹：（在 获得奖励 ）

TD(0)： - 只有 被直接更新 - 需要多次迭代后才受影响

Sarsa()（假设 ）：

假设在 时：

$$

e_3(S_3) = 1, e_3(S_2) = 0.81, e_3(S_1) = 0.729 $$

TD 误差（假设初始 ）：

所有状态同时更新：

$$

V(S_3) + = 10

V(S_2) + = 8.1

V(S_1) + = 7.29 $$

一步就将奖励信号传播到了整条轨迹！

实践效果：

• 在长轨迹任务中， Sarsa() 比 Sarsa(0)快几倍到几十倍
• 通常效果最好
• 代价：需要为每个状态维护资格迹（内存开销）

---

Q7：如何选择合适的探索策略？ε-贪婪有哪些替代方案？

ε-贪婪的问题：

• 探索是均匀随机的（没有利用先验知识）
• 固定时，后期仍会做无效探索
• 对所有动作等概率探索（即使明显差的动作）

改进方案：

1. 衰减 ε-贪婪：

随时间降低探索率：

常见设置：。

2. Boltzmann 探索（ Softmax）：

根据 Q 值的相对大小选择动作：

$$

P(a|s) = $$

温度参数 ： - : 接近贪婪 - : 接近均匀随机

优点： Q 值高的动作有更高的选择概率。

3. UCB（ Upper Confidence Bound）：

基于不确定性的探索：

$$

a^{*} = _a $$

其中 是动作 在状态 被选择的次数。

直觉：探索那些不确定的动作（访问次数少）。

4. 噪声网络（ NoisyNet）：

在网络参数中加入可学习的噪声（详见第六章）。

实践建议：

场景	推荐方法	原因
简单任务	ε-贪婪 + 衰减	简单有效
连续动作空间	参数噪声（如 OU 噪声）	ε-贪婪不适用
深度 RL	NoisyNet	探索与策略参数耦合
样本昂贵	UCB	最优探索效率
多臂老虎机	Thompson 采样	贝叶斯最优

---

Q8： TD 方法的"有偏性"在实践中有多大影响？

TD 方法的偏差来源于 bootstrapping：用当前估计 代替真实价值 。

偏差分析：

假设真实价值为 ，当前估计为 ， TD 误差：

TD 目标的偏差：

初始时偏差可能很大，但随着 逼近 ，偏差消失。

方差对比：

MC 方差（假设 步轨迹）：

TD 方差：

TD 方差比 MC 低 倍！

实践影响：

在大多数任务中，低方差比无偏性更重要：

• 深度 RL：函数逼近器（神经网络）会放大方差
• 长 episode： MC 的方差随 episode 长度线性增长
• 样本效率： TD 能从相同样本数中学到更多

经验结论：

• TD 方法通常比 MC 更快收敛（尤其是 TD(), ）
• 在高方差任务中， TD 的优势更明显
• MC 在短 episode 、离线数据场景中仍有价值

---

Q9：如何设置学习率 ？固定学习率和自适应学习率各有什么优缺点？

学习率控制每次更新的步长，对收敛性和稳定性至关重要。

理论要求（ Robbins-Monro 条件）：

保证收敛的充要条件：

满足条件的例子：

• ：经典衰减
• ：基于访问次数

固定学习率：

优点： - 简单 - 能适应非平稳环境（近期样本权重更大）

缺点： - 不满足 Robbins-Monro 条件（理论上不保证收敛到最优） - 最终会在最优解附近振荡

常用值：，通过交叉验证确定。

自适应学习率：

1. 基于访问次数：

其中 是状态 被访问的次数。

优点： - 满足 Robbins-Monro 条件 - 频繁访问的状态学习率自动降低

缺点： - 后期学习慢 - 需要维护访问计数

2. AdaGrad 风格：

借鉴深度学习的自适应优化器：

其中 是梯度（或 TD 误差）。

3. Adam 风格：

使用一阶和二阶矩估计：

$$

m_t = 1 m{t-1} + (1 - _1) g_t

v_t = 2 v{t-1} + (1 - _2) g_t^2 _t = $$

实践建议：

场景	推荐方法	参数
简单表格 RL	固定学习率
深度 RL	Adam 优化器
在线学习	固定学习率
离线学习	衰减学习率	初始 0.1，衰减到 0.001
非平稳环境	固定学习率	保持适应性

调优技巧：

• 从较大的学习率开始（如 0.1），观察训练曲线
• 如果不稳定/发散，降低学习率
• 如果收敛太慢，增大学习率
• 使用 learning rate schedule（如线性衰减、指数衰减）

---

Q10：马尔可夫性假设在实际问题中经常不满足，如何处理部分可观测问题？

部分可观测马尔可夫决策过程（ POMDP）：

智能体不能直接观察状态 ，只能观察到观测 ，观测与状态的关系由观测函数决定：

$$

O(o|s, a) $$

示例： - 机器人导航：传感器读数（观测）≠ 真实位置（状态） - 医疗诊断：症状（观测）≠ 疾病（状态） - 金融交易：市场数据（观测）≠ 市场状态（状态）

解决方案：

1. 状态增强（ State Augmentation）：

将历史观测拼接为扩展状态：

在深度 RL 中常用帧堆叠（ frame stacking）：

# Atari 游戏：堆叠最近 4 帧
state = np.concatenate([frame_t, frame_{t-1}, frame_{t-2}, frame_{t-3}], axis=0)

优点：简单，适用于短期记忆 缺点：状态空间维度爆炸

2. 循环神经网络（ RNN）：

使用 LSTM/GRU 处理观测序列，隐藏状态 作为状态表示：

$$

h_t = (o_t, h_{t-1}) (a|h_t), V(h_t) $$

优点：能处理长期依赖 缺点：训练困难（梯度消失/爆炸）

3. 信念状态（ Belief State）：

维护状态的概率分布（信念）：

$$

b(s) = P(S_t = s | o_1, a_1, , o_t) $$

使用贝叶斯更新：

$$

b'(s') = $$

在信念空间上求解 MDP 。

优点：理论完备 缺点：计算复杂度高（连续状态空间不可行）

4. Transformer（现代方法）：

使用自注意力机制处理观测序列：

优点：能捕捉长距离依赖，并行化训练 缺点：计算开销大

实践建议：

场景	推荐方法	示例
短期部分可观测	帧堆叠	Atari 游戏（堆叠 4 帧）
长期记忆需求	LSTM/GRU	对话系统、策略游戏
高度不确定性	信念状态	机器人定位（ SLAM）
大规模序列	Transformer	决策 Transformer

诊断方法：

如果怀疑马尔可夫性不满足，检查：

• 智能体是否会在相同观测下做出不同决策？
• 奖励信号是否延迟很久才出现？
• 环境是否有隐藏状态（如对手意图）？

如果是，考虑状态增强或 RNN 。

🎓 总结：强化学习核心要点

MDP 框架：

强化学习的核心是马尔可夫决策过程 ，智能体通过策略 与环境交互，目标是最大化累积回报 。

Bellman 方程（记忆公式）：

$$

V^(s) = a (a|s) {s'} P(s'|s, a) [R + V^(s')]

V^{*}(s) = a {s'} P(s'|s, a) [R + V^{*}(s')] $$

方法论三角：

        动态规划（已知模型）
       /                \
      /                  \
蒙特卡洛（无模型，高方差）  时序差分（无模型，低方差）

实战 Checklist：

• 明确状态空间、动作空间、奖励函数
• 选择折扣因子 （ 0.9-0.99）
• 如果模型已知，用动态规划
• 如果模型未知且 episode 短，用 MC
• 如果模型未知且任务连续，用 TD（ Q-Learning/Sarsa）
• 设计合适的探索策略（ε-贪婪 + 衰减）
• 调优学习率 （从 0.1 开始）
• 对于长轨迹，考虑资格迹（ Sarsa()）

核心直觉（记忆口诀）：

价值 = 即时奖励 + 未来折扣价值

策略改进 = 贪婪选择高价值动作

学习 = 用经验修正估计（ MC/TD）

下一章预告：

第一章建立了强化学习的理论基础，但所有方法都局限于小规模的表格型问题（状态和动作数量有限）。当状态空间巨大（如 Atari 游戏的像素空间）或连续时，表格方法无法扩展。

下一章将介绍如何用深度神经网络逼近 Q 函数，诞生了深度强化学习的开山之作—— DQN（ Deep Q-Network）。我们将深入探讨：

• 深度 Q 网络的架构
• 经验回放和目标网络的作用
• DQN 的变体： Double DQN 、 Dueling DQN 、 Prioritized Experience Replay
• Rainbow：集大成者
• 完整的 Atari 游戏实现

📚 参考文献

1. Sutton, R. S., & Barto, A. G. (2018). Reinforcement Learning: An Introduction (2nd ed.). MIT Press.
2. Watkins, C. J., & Dayan, P. (1992). Q-learning. Machine Learning, 8(3-4), 279-292.
3. Sutton, R. S. (1988). Learning to predict by the methods of temporal differences. Machine Learning, 3(1), 9-44.
4. Sutton, R. S., Precup, D., & Singh, S. (1999). Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artificial Intelligence, 112(1-2), 181-211.
5. Bellman, R. (1957). Dynamic Programming. Princeton University Press.
6. Silver, D. (2015). UCL Course on Reinforcement Learning. https://www.davidsilver.uk/teaching/
7. Levine, S. (2023). CS 285: Deep Reinforcement Learning. UC Berkeley.
8. Dayan, P. (1992). The convergence of TD() for general. Machine Learning, 8(3-4), 341-362.

---

本文是强化学习系列的第一篇，为整个系列奠定理论基础。后续章节将深入探讨深度强化学习、策略优化、探索策略、多智能体学习等前沿主题。