学习率：从入门到大模型训练的终极指南

学习率（Learning Rate, LR）是深度学习里最重要、也最容易“看起来像玄学”的超参数。它既像汽车的油门（决定你每一步走多快），也像方向盘的灵敏度（太敏感会蛇形走位甚至翻车，太迟钝又永远到不了目的地）。

这篇文章会从最简单的二次函数出发，把“学习率为什么会影响稳定性、为什么训练后期要降学习率、为什么 warmup 常见”讲清楚。

---

一句话把学习率讲清楚

把训练想象成“在雾里下山”：

• 参数 是你的位置；
• 损失 是海拔（越低越好）；
• 梯度 是“坡度方向提示”；
• 学习率 是“你每一步迈多大”。

你每一步大致按下面走：

其中 是你看到的梯度（通常是小批量 mini-batch 的随机梯度）。

学习率的核心矛盾就一句话：

越大越快，但越容易不稳定； 越小越稳，但越慢、也可能卡住。

接下来我们用“从最简单的二次函数”开始，把这句话拆开讲透。

---

最小可用数学：为什么“太大就炸，太小就慢”

¶从一维抛物线开始（最重要的直觉）

考虑最简单的损失：

梯度是：

做梯度下降：

你看到一个关键系数：。它决定了收敛还是发散：

• 若 ，会收敛；
• 若 ，会发散（来回跳并越跳越大）。

于是得到稳定条件：

类比：你下山时每一步都按“坡度”迈。如果坡太陡（ 大），同样的步幅（）更容易跨过谷底到另一边再反弹；坡越缓（ 小），你可以迈更大步仍然不翻车。

¶多维情况下，“最陡的方向”决定是否爆炸

把 推广到多维二次型：

其中 是 Hessian（曲率矩阵）。稳定性由最大特征值 主导：

一句话：训练是否会炸，往往由“最陡那条方向”决定。

类比：你在山谷里走路，整体看起来很平缓，但某一条方向上突然很陡（比如悬崖边）。你迈步时只要有分量朝那条方向，就可能摔下去。

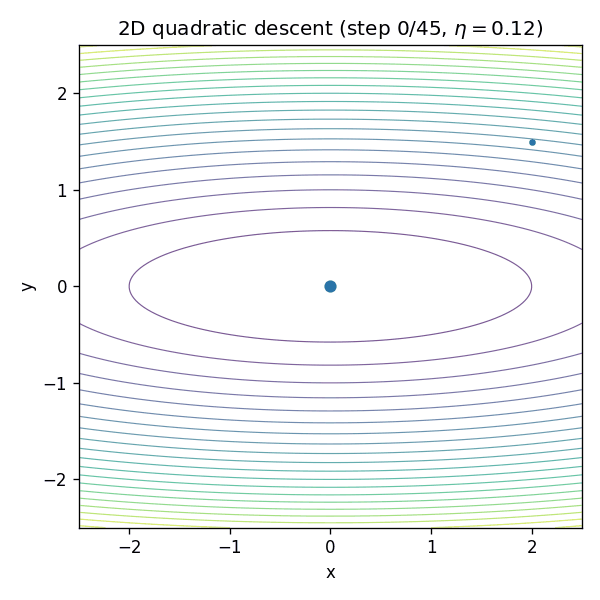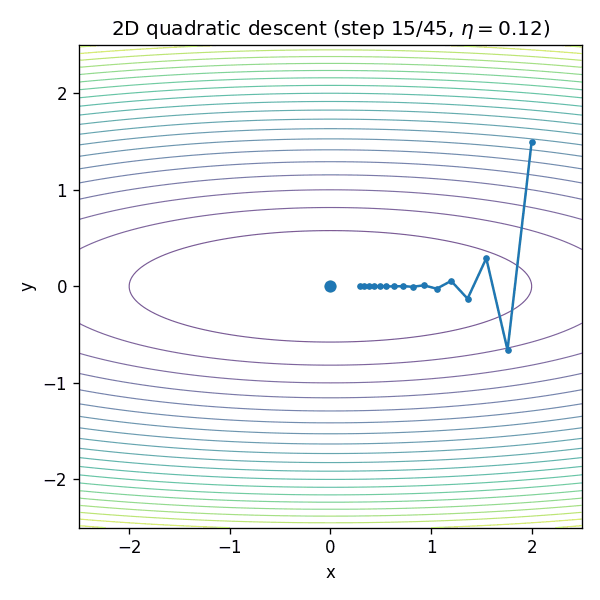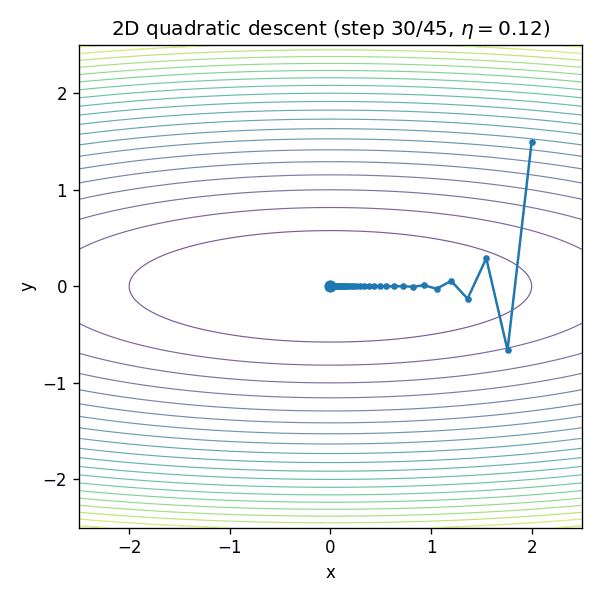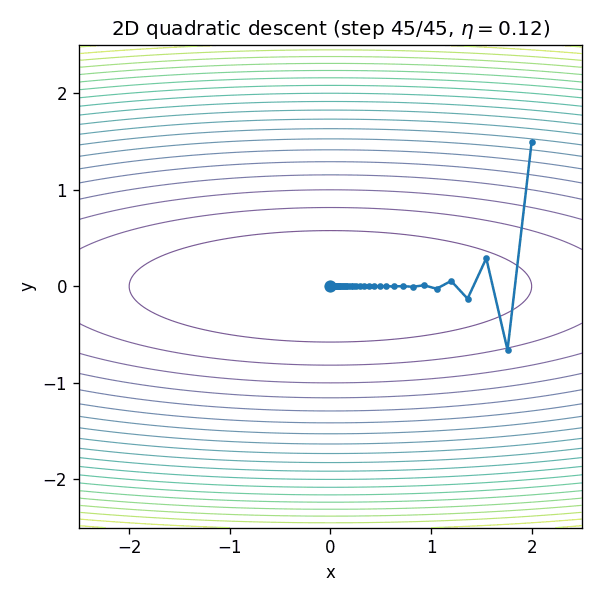
¶GIF：二维“椭圆谷底”里为什么会走成“之”字

二维二次函数是理解“曲率不均匀导致震荡”的最佳玩具模型。考虑：

当 时， 方向更“陡”，同一个学习率 会在 方向产生更强的回弹，于是轨迹常常呈现“之”字形（尤其是没加动量时）。

import numpy as np

ax, ay = 1.0, 12.0
eta = 0.12
x = np.array([2.0, 1.5])

path = [x.copy()]
for _ in range(45):
    g = np.array([ax * x[0], ay * x[1]])
    x = x - eta * g
    path.append(x.copy())

¶为什么深度网络更难：曲率在训练中会变

真实神经网络不是二次函数， 会随训练变化；更麻烦的是：

• 梯度是随机的（mini-batch）；
• 不同层/不同参数的“有效尺度”差异巨大；
• 还会有动量、归一化、权重衰减、裁剪等“附加物理”。

所以现代训练几乎不会只用一个常数学习率跑到底，而是用学习率调度（schedule）： 随时间变化。

¶更进一步：-光滑（L-smooth）告诉你“学习率上限”从哪来

上面的二次函数例子有个隐藏前提：曲率 固定不变。更一般地，优化里常见一个假设叫 -光滑：

梯度不会变化得太快（损失曲线不会突然“折成直角”）。

一种常见表述是：对任意 ，有

这意味着“局部曲率”不会超过某个上界 （你可以把 理解为“最陡的最大程度”）。在这种情况下，梯度下降取

通常就能保证每步不至于把损失抬高（直观上是“别一步跨太大”）。

类比：你在一个城市里开车， 像“这座城市里最陡的下坡路的坡度上限”。如果你把油门踩到超过这个城市道路条件能承受的程度，你迟早会在某个最陡路段失控。

¶强凸（strongly convex）与“为什么后期需要降低学习率”

如果函数在最优点附近像一个“碗”，并且碗的曲率不会太小（-强凸），那么会有更快的收敛性质。你可以把这理解成：

• 碗太浅：你靠近最低点后，坡度很小，继续用大步长会来回晃；
• 碗够“硬”：你能更快被拉回最低点附近。

很多理论告诉我们：在随机梯度（有噪声）下，学习率通常需要逐步变小，才能把“最后那点抖动”压下去。这就是 schedule 后期 decay/cooldown 的一个根源：让你从“探索”切换到“精修”。

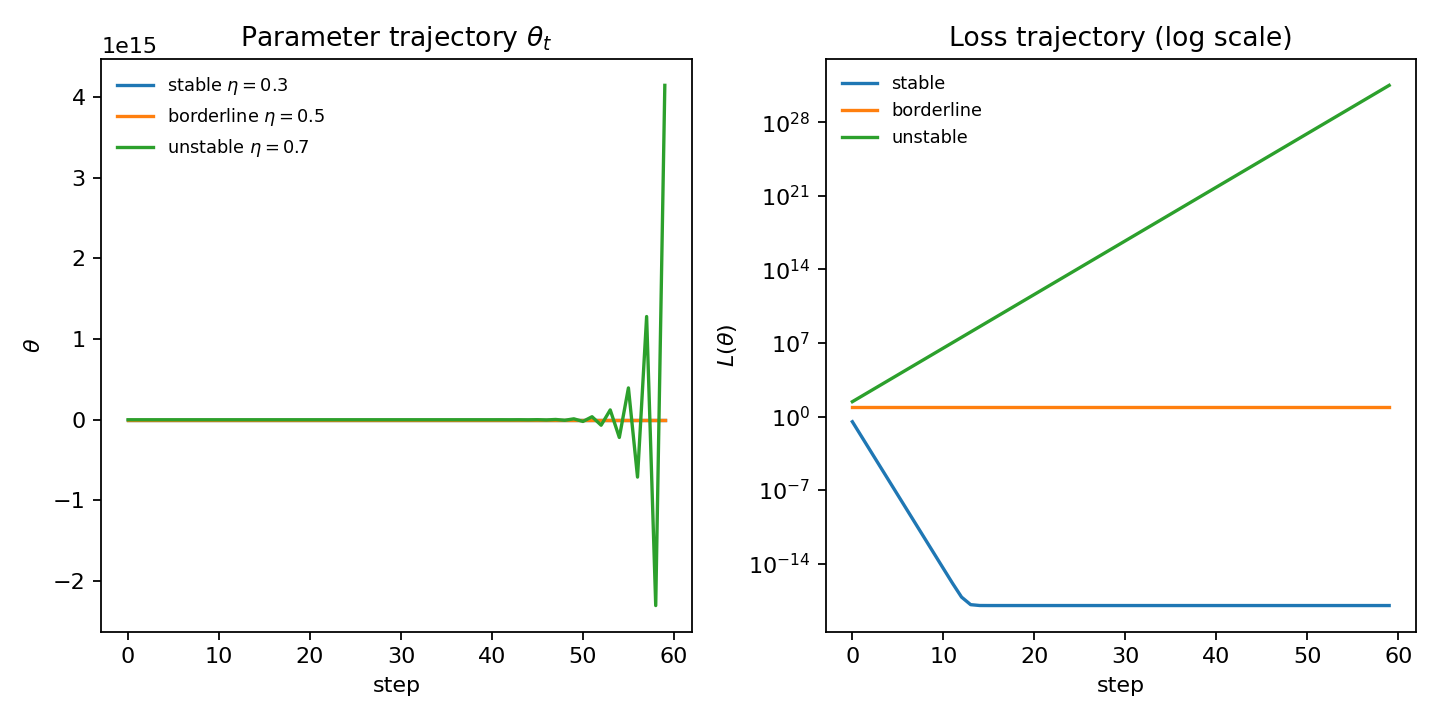
¶一维二次函数里“稳定 / 临界 / 发散”长什么样

用 这个最简单模型，你可以用一小段代码亲眼看到：

• 稳定：，参数与 loss 都会快速衰减；\
• 临界：，会在谷底两侧来回“弹跳”，loss 降得很慢；\
• 发散：，振幅越来越大，loss 直接爆炸。

import matplotlib.pyplot as plt
import numpy as np

a = 4.0
steps = 60
theta0 = 2.0
etas = [0.3, 2.0 / a, 0.7]  # stable / borderline / unstable

def run(eta: float):
    theta = theta0
    thetas, losses = [], []
    for _ in range(steps):
        g = a * theta
        theta = theta - eta * g
        thetas.append(theta)
        losses.append(0.5 * a * theta * theta)
    return np.array(thetas), np.array(losses)

ths1, l1 = run(etas[0])
ths2, l2 = run(etas[1])
ths3, l3 = run(etas[2])

plt.figure(figsize=(9, 4.5), dpi=160)
plt.subplot(1, 2, 1)
plt.plot(ths1, label=f"stable eta={etas[0]:.2f}")
plt.plot(ths2, label=f"borderline eta={etas[1]:.2f}")
plt.plot(ths3, label=f"unstable eta={etas[2]:.2f}")
plt.title("Parameter trajectory $\\theta_t$")
plt.xlabel("step")
plt.ylabel("$\\theta$")
plt.legend(frameon=False, fontsize=8)

plt.subplot(1, 2, 2)
plt.semilogy(l1 + 1e-18, label="stable")
plt.semilogy(l2 + 1e-18, label="borderline")
plt.semilogy(l3 + 1e-18, label="unstable")
plt.title("Loss trajectory (log scale)")
plt.xlabel("step")
plt.ylabel("$L(\\theta)$")
plt.legend(frameon=False, fontsize=8)

plt.tight_layout()
plt.savefig("gd_stability_1d.png")
plt.close()

---

学习率与“噪声”：为什么 batch size 会影响学习率

¶随机梯度的两张脸：方向有用，噪声也很大

mini-batch 梯度可以看成：

其中 是噪声（随机性）。这件事带来两种效应：

• 好处：噪声让你不容易困在“很尖的坏坑”，像在地形里加了点抖动；
• 坏处：噪声让大步长更容易“抖飞”，训练不稳定。

类比：你蒙眼下山，手里拿指南针（梯度方向），但指南针会抖（噪声）。你走得越快（学习率大），抖动造成的偏差越大。

¶经典经验：线性缩放法则与 warmup（大 batch 训练）

很多设置里，增大 batch size 可以减少梯度噪声，因此人们常用经验：

• batch 变大 倍，学习率也乘 （线性缩放）；
• 但训练初期“系统还没稳定”，所以先用 warmup 把学习率从小慢慢升到目标值。

warmup 的典型形式（线性 warmup）：

近年的研究进一步解释了 warmup 的作用：它往往不是“为了收集 Adam 的统计量”这么简单，而是帮助模型进入更“好条件”的区域，从而能承受更大的目标学习率（见后文“最新进展”部分）。

---

动量：学习率的“隐形放大器”

¶SGD + Momentum 的更新与直觉

动量（以经典形式为例）：

其中 常取 0.9。

类比：你推一个很重的购物车下坡：

• 是你当下看到的坡度；
• 是车的速度（带惯性）；
• 越大，车越“刹不住”，但也越能穿过小坑洼；
• 学习率 相当于“你给速度换算成位移的比例”。

¶为什么动量会让你更容易“过冲”

直觉上，动量会把一段时间内的梯度方向叠加起来，相当于“长期沿一个方向加速”。因此：

• 同样的 ，加动量后等效步长更大；
• 所以很多时候 SGD+momentum 的可用学习率上限会更低，否则会更容易震荡。

这也是为什么一些训练 recipe 会写：

• SGD 的 base LR 比 AdamW 大；
• 但 SGD + momentum 需要更谨慎的 warmup/decay；
• 或者配合更强的正则化（weight decay、label smoothing 等）稳住。

---

自适应优化器：学习率“变成一组学习率”

如果说 SGD 的学习率是一把锤子（全局同一个 ），那么 Adam 类方法像是一套“带扭矩控制的电动螺丝刀”：不同参数会自动用不同的步长。

¶Adam 的核心公式（一定要看懂）

Adam（省略一些细节，只保留关键结构）：

其中 表示逐元素平方； 是偏置修正后的估计。

你应该抓住一句话：

Adam 的“有效学习率”大致是 ，所以每个参数的步长会随其梯度尺度自动缩放。

类比：同一辆车在不同路面（不同参数维度）行驶。路面越颠（梯度方差越大），系统自动把那一侧轮子的扭矩（步长）调小，避免打滑。

¶为什么 Adam 仍然需要 warmup（而且经常更需要）

很多人以为：Adam 都自适应了，为什么还要 warmup？

一个关键原因：训练初期的统计量不稳定 + 某些方向的“预条件化曲率”很大，导致你如果一上来就用目标学习率，容易出现大幅抖动（loss spike）甚至训练失败。

这也是近年关于 warmup 的理论解释里经常出现的关键词：sharpness / preconditioned sharpness（可理解为“有效曲率”）。

---

学习率调度（schedule）大全：从老办法到大模型默认

把 schedule 看成“训练过程的配速策略”：

• 前期：探索更大范围（跑得快）
• 中期：稳定推进（匀速）
• 后期：精细收敛（减速、微调）

先看一张“最常用曲线”对比图（同样由 生成）：

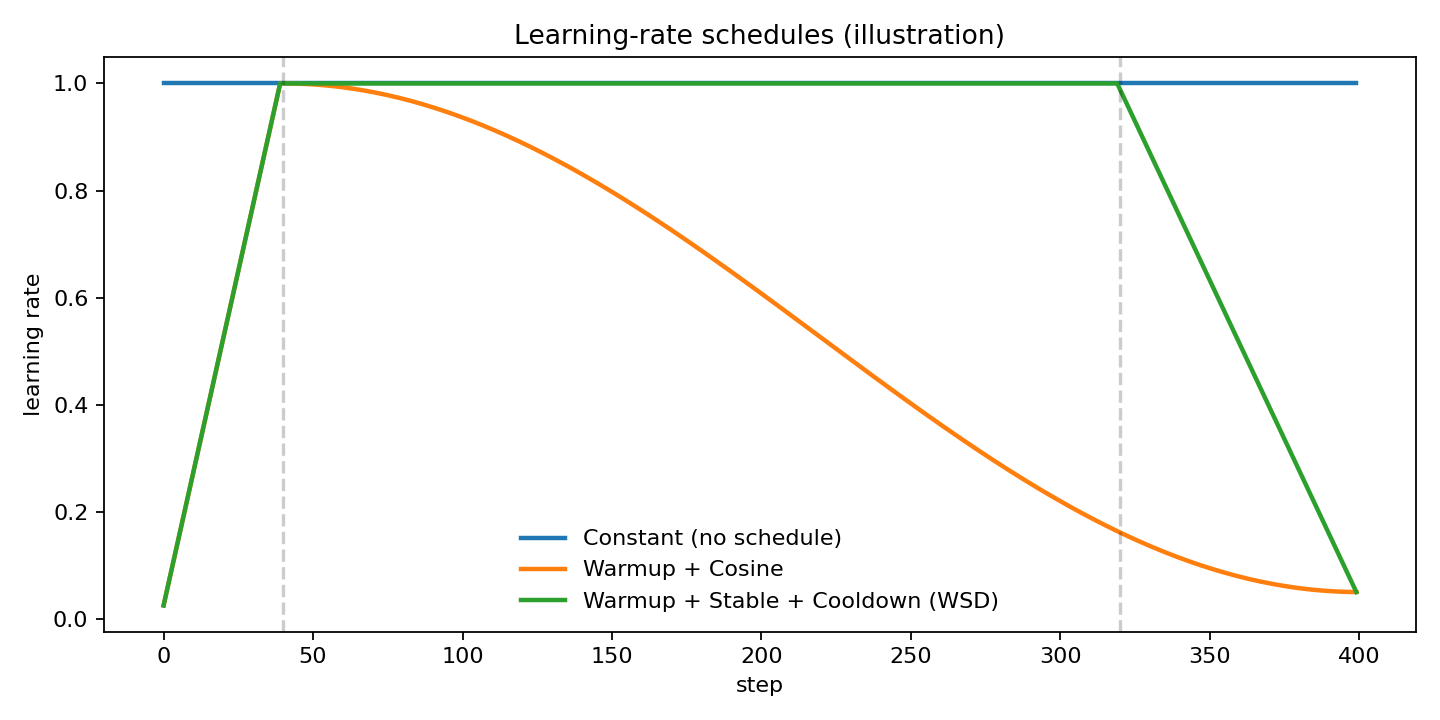
¶常数学习率（Constant）

优点：简单。

缺点：几乎总会在“速度 vs 稳定”之间两难：要么前期太慢，要么后期太抖。

¶Step decay（台阶式）

例如每到某些 epoch 乘以 ：

类比：跑步时每过一段路程突然把速度降一档。

优点：实现简单。

缺点：变化不平滑，可能造成训练指标突然波动。

¶Exponential decay（指数衰减）

优点：平滑。

缺点：后期可能衰得太快，等效“刹车过早”，尤其在长训练中。

¶Cosine decay（余弦退火，深度学习最常用之一）

（最常见版本：从峰值衰到一个最小值）

直觉：一开始减速慢（保持探索），后面减速快（冲向收敛）。

大模型训练中常见结构是：

• warmup：线性升到
• cosine：从 退到

¶Cosine warm restarts（SGDR）

余弦衰到低点后又“重启”到高学习率，再衰一次。

直觉：像周期性“冲坡”，有时能跳出局部坏盆地。

在现代大模型预训练中，不如纯一次性 cosine / WSD 常见，但在一些中小模型与某些任务上仍有价值。

¶One-cycle（超级收敛思想）

核心：学习率先升后降（并配合动量反向变化）。

直觉：前期把学习率推到接近稳定边界，加速探索；后期快速降下来收敛。

很适合“训练步数较短、希望快速到一个不错解”的场景。

¶逆平方根（Transformer 经典 schedule）

在 Transformer 早期训练 recipe 中很常见的一类形式（示意）：

直觉：warmup 后开始按 缓慢衰减。

这类 schedule 的精神是：长期训练别衰太快。

¶WSD（Warmup–Stable–Decay）：近年大模型训练的重要趋势

WSD 的核心形状：

• warmup：上升
• stable：长时间保持常数学习率
• decay/cooldown：最后线性（或其他形式）降到很小

直觉：中段“匀速巡航”，最后“进站刹车”。

为什么它近年很受欢迎？

• 它比 cosine 更“可复用”：你可以先训练一段稳定期，后面想延长训练时不必从头设计一个依赖总步数的半周期 cosine。
• 很多工作观察到 cooldown 开始时损失会出现“明显下降”，像模型终于被允许“精细贴合”盆地。

（后文会结合 2025 的理论解释更详细讲。）

---

从“能跑”到“跑得好”：一套可操作的学习率调参流程

下面给一套你可以在绝大多数任务里复用的流程（从小白视角写，但足够深）。

¶先搞清楚：你训练失败到底是哪种失败？

训练“坏掉”常见有三类：

1. 直接发散：loss 变成 NaN/inf，或者几步内冲天。
2. 抖动不收敛：loss 在高位大幅波动，指标上不去。
3. 看似稳定但学不动：loss 缓慢下降甚至平台期很早出现。

对应的学习率结论通常是：

• (1)(2)： 太大（或动量太大、或缺少 warmup、或裁剪/正则不够）
• (3)： 太小（或 schedule 衰减太快、或 batch 太小噪声太大）

¶用 “LR range test” 快速找可行区间（强烈推荐）

经典做法：在很短的训练里，让学习率从很小指数增长到很大，观察 loss 什么时候开始明显上升/发散。

直觉：你在“试探油门”，找到“刚好不翻车”的上限。

简化版伪代码（PyTorch）：

import math
import torch

def lr_range_test(model, loader, loss_fn, optimizer, lr_min=1e-7, lr_max=10, num_steps=200):
    model.train()
    # 指数增长
    mult = (lr_max / lr_min) ** (1 / (num_steps - 1))
    lr = lr_min
    for g in optimizer.param_groups:
        g["lr"] = lr

    losses = []
    lrs = []
    it = iter(loader)
    for step in range(num_steps):
        try:
            x, y = next(it)
        except StopIteration:
            it = iter(loader)
            x, y = next(it)

        optimizer.zero_grad(set_to_none=True)
        pred = model(x)
        loss = loss_fn(pred, y)
        loss.backward()
        optimizer.step()

        losses.append(loss.item())
        lrs.append(lr)

        lr *= mult
        for g in optimizer.param_groups:
            g["lr"] = lr

    return lrs, losses

你会得到一个曲线：

• 初期 loss 下降（学习开始）
• 到某个点开始抖动甚至上升（接近稳定边界）

经验：把“刚开始明显变差前”的学习率当作 的量级，然后正式训练用它的 0.3～1 倍（按任务调整）。

¶选择 schedule：小模型 vs 大模型的经验差异

• 中小模型（训练步数不算特别长）：cosine / one-cycle 往往很稳妥。
• 大模型预训练（训练极长、可能要多次续训）：WSD 或 schedule-free 值得优先考虑。

一个很实用的默认（尤其是 AdamW）：

• warmup：1%～5% steps（大 batch 或很深模型倾向更长）
• stable：大部分训练保持
• cooldown：最后 10%～20% steps 线性降到 （比如 的 0.1 倍或更小）

¶“学习率、batch、权重衰减”三者要一起看

很多人只调学习率，然后觉得“怎么总是不稳”。实际上这三者高度耦合：

• batch 影响梯度噪声；
• weight decay 影响参数尺度（等价于持续把参数往 0 拉）；
• 学习率决定你每一步“顺着梯度走多远”。

类比：你驾驶一辆车：

• learning rate 是油门；
• batch size 是路面摩擦/风噪（稳定性）；
• weight decay 像一直有个刹车在轻踩（让车别越跑越飘）。

不稳定时不要只想着“降学习率”，很多时候：

• 加一点梯度裁剪（clip norm）
• 适当加 weight decay
• 或者延长 warmup

会比一味降 更好，因为降 往往会牺牲最终效果或训练效率。

---

代码：从零实现常用 schedule（PyTorch）

下面给一个“够用且清晰”的实现：warmup + cosine / warmup + WSD（cooldown 线性）。

¶Warmup + Cosine

import math

def lr_warmup_cosine(step, total_steps, warmup_steps, lr_max, lr_min=0.0):
    if step < warmup_steps:
        # 线性 warmup
        return lr_max * (step + 1) / max(1, warmup_steps)

    # cosine decay
    t = step - warmup_steps
    T = max(1, total_steps - warmup_steps)
    cos = 0.5 * (1.0 + math.cos(math.pi * t / T))
    return lr_min + (lr_max - lr_min) * cos

¶Warmup + Stable + Decay（WSD）

def lr_wsd(step, total_steps, warmup_steps, cooldown_steps, lr_max, lr_min=0.0):
    # warmup
    if step < warmup_steps:
        return lr_max * (step + 1) / max(1, warmup_steps)

    # stable
    stable_end = total_steps - cooldown_steps
    if step < stable_end:
        return lr_max

    # cooldown: 线性衰减到 lr_min
    t = step - stable_end
    T = max(1, cooldown_steps)
    frac = min(1.0, (t + 1) / T)
    return lr_max + (lr_min - lr_max) * frac

¶把它接到 optimizer 上（训练循环骨架）

import torch

def train_one_epoch(model, loader, optimizer, step_offset, total_steps, schedule_fn, device="cuda"):
    model.train()
    step = step_offset
    for x, y in loader:
        x, y = x.to(device), y.to(device)

        lr = schedule_fn(step, total_steps)
        for g in optimizer.param_groups:
            g["lr"] = lr

        optimizer.zero_grad(set_to_none=True)
        pred = model(x)
        loss = torch.nn.functional.cross_entropy(pred, y)
        loss.backward()

        # 可选：梯度裁剪，常用于大模型稳定性
        torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)

        optimizer.step()
        step += 1

    return step

你可以像这样传入 schedule：

schedule_fn = lambda step, total_steps: lr_wsd(
    step=step,
    total_steps=total_steps,
    warmup_steps=int(0.02 * total_steps),
    cooldown_steps=int(0.10 * total_steps),
    lr_max=3e-4,
    lr_min=3e-5,
)

---

最新研究进展：大家在“学学习率”什么？

如果你把学习率看成“油门曲线”，那么近年的研究大致沿着三条路在推进：

1. 更好的油门曲线：cosine 之外，WSD、power-law family、token/batch agnostic schedule。
2. 把油门交给系统：schedule-free（不需要指定总步数的 schedule）、甚至 learning-rate-free（让算法自动估计合适步长）。
3. 解释为什么有效：warmup、cooldown 的机制解释，稳定边界、曲率/尖锐度（sharpness）视角，和大模型不稳定的预测。

下面按时间线串起来。

¶2023：Learning-rate-free 的代表——D-Adaptation

一句话：尽量不让你手动调 base learning rate。

D-Adaptation（2023，Meta）提出用一种理论驱动的方式自动估计步长尺度，使得在很多任务上能接近手调学习率的效果。

你可以把它理解成：传统方法需要你告诉系统“从起点到终点大概有多远”（步长尺度），而 D-Adaptation 试图在训练过程中估计这个“距离尺度”，从而自动设定合适的步长。

参考：Learning Rate-Free Learning by D-Adaptation (Meta, 2023)

¶2024：Schedule-Free AdamW（The Road Less Scheduled）

经典痛点：很多 schedule 需要你提前知道总训练步数 （例如 cosine 的半周期要对齐训练长度）。但现实中你经常会：

• 训练到一半发现还想继续；
• 或者想做不同训练预算的对比；
• 或者数据/算力不确定。

Schedule-Free AdamW（2024）提出一种做法：干脆不显式做 schedule，但性能能与有 schedule 的方法竞争。

直觉理解：它把“调度”和“迭代平均”等思想统一起来，让算法在不需要知道停止时间 的情况下，仍能走出类似“先快后慢”的有效轨迹。

参考：Schedule-Free AdamW (arXiv:2405.15682)

¶2024：Why Warmup?——warmup 机制被更系统地解释

2024 的一条重要结论是：warmup 的主要收益往往是让网络能承受更大的目标学习率，而不是仅仅“让 Adam 统计量更准”。

这会改变你调参的思路：

• 你不是在问“warmup 要不要”
• 而是在问“我希望最终的 能有多大、稳定边界在哪，warmup 帮我把边界推到哪里”

参考：Why Warmup the Learning Rate? (arXiv:2406.09405)

¶2024：Power Scheduler——对 batch size 与 token 数不敏感

大模型预训练的现实痛点是：你经常会换 batch size、换训练 tokens（预算变化），而最优学习率也会跟着漂移。

Power Scheduler（2024）发现并利用一种 学习率、batch size、训练 tokens 的幂律关系，构建出对 batch/token 更“免调”的调度方式，并强调与 P 等参数化结合的可迁移性。

参考：Power Scheduler (arXiv:2408.13359)

¶2023–2024：用“小模型复现大模型不稳定”——学习率稳定性研究

大模型训练常见“同样超参，小模型没事，大模型炸了”的现象。Wortsman 等工作提出：很多不稳定性其实能在小模型里通过更高学习率复现，从而可以用更低成本研究：

• 哪些干预能降低对学习率的敏感性（warmup、weight decay、参数化等）；
• 能否在训练早期通过某些信号预测后续不稳定。

参考：Small-scale proxies for large-scale Transformer instabilities (arXiv:2309.14322)

¶2024：No More Adam?——把关键放回“学习率尺度”

一条很“反直觉但很有启发”的路线是：也许 Adam 的优势很大部分来自“不同参数组的有效学习率尺度被自动调平”。

2024 的 SGD-SaI 提出在初始化时基于某种信号（例如 g-SNR）对不同参数组做学习率缩放，从而用更接近 SGD 的方法获得接近 AdamW 的效果，并且显著减少优化器状态的显存占用。

这对学习率研究的意义是：学习率不只是一个数，而是一个“与参数尺度/信噪比耦合的系统设计问题”。

参考：No More Adam / SGD-SaI (arXiv:2412.11768)

¶2025：cosine vs WSD 的理论联系（凸优化视角）

2025 的一条很有意思的观察是：一些大模型训练中的学习率曲线（尤其是 WSD 的 cooldown）在形状上和某些凸优化理论界非常接近，并且 cooldown 的收益在界里体现为“去掉了对数项”等。

你不需要完全理解那套界，但你可以记住结论：

• WSD 的 cooldown 不是“玄学的最后一脚刹车”，它能在一些理论模型中被解释为更好的收敛项；
• 这也提供了在不同 schedule 间迁移 base learning rate 的思路。

参考：Convex theory view of WSD cooldown (arXiv:2501.18965)

---

FAQ：最常见的学习率问题（小白高频）

¶“我该用 AdamW 还是 SGD？”

如果你是小白并且目标是“先跑通、稳定产出”：

• 默认：AdamW + warmup + cosine/WSD。

如果你追求更低显存、更强可解释性、或在某些视觉任务上想追极致：

• SGD（通常配动量）仍然很强，但更依赖调参经验。

¶“loss 一开始就炸怎么办？”

按优先级排查（从最有效到次要）：

• 把 降一个数量级试试；
• 增加 warmup（或把 warmup 起点设得更小）；
• 打开梯度裁剪；
• 检查混合精度（loss scaling）与数值稳定；
• 适当增加 weight decay（尤其是大模型）。

¶“loss 不炸但不怎么降怎么办？”

常见原因：

• 学习率太小；
• 衰减太快（过早进入小学习率阶段）；
• batch 太小导致噪声很大，模型“原地抖动”；
• 数据/标签问题（这不是学习率能救的）。

策略：

• 做 LR range test 找上限；
• 让中段更长时间保持在较大 （WSD 的 stable 部分很适合）。

---

一页速查表（把“怎么选学习率”落地）

¶AdamW 常见起手式（通用）

• schedule：warmup + cosine 或 warmup + WSD
• warmup：1%～5%
• cooldown（若用 WSD）：10%～20%
• 梯度裁剪：（大模型常用）

¶你应该关注的 3 个指标（比“看 loss”更直接）

• 训练是否接近稳定边界：是否出现持续的 loss spike / 梯度范数爆炸迹象
• 有效步长是否过小：学习太慢、长期平台
• 对学习率的敏感性：轻微改动 是否导致结果大幅变化（越敏感越说明你在边界附近/系统不稳）

¶当你不知道选 cosine 还是 WSD

• 训练长度固定、不会续训：cosine 很稳妥；
• 训练长度可能变化、需要续训/多预算对比：优先 WSD；
• 想尽量少调 schedule：可以关注 schedule-free / learning-rate-free 方向（但要看你代码栈是否方便接入）。

---

参考资料（按本文提到的关键脉络）

• Learning Rate-Free Learning by D-Adaptation (Meta, 2023)
• Schedule-Free AdamW (arXiv:2405.15682)
• Why Warmup the Learning Rate? (arXiv:2406.09405)
• Power Scheduler (arXiv:2408.13359)
• Small-scale proxies for large-scale Transformer instabilities (arXiv:2309.14322)
• Convex theory view of WSD cooldown (arXiv:2501.18965)
• No More Adam / SGD-SaI (arXiv:2412.11768)